CS 132 Spring 2008 Chapter 11 Binary Trees

CS 132 Spring 2008 Chapter 11 Binary Trees p. 631 -666 1

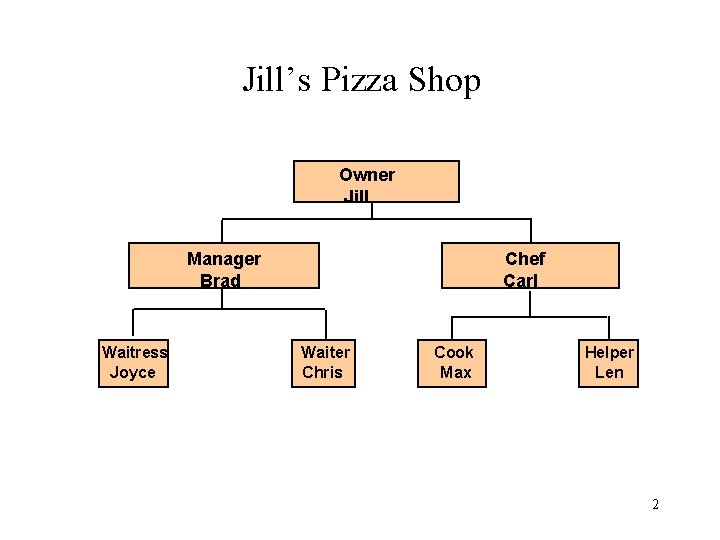
Jill’s Pizza Shop Owner Jill Manager Brad Waitress Joyce Chef Carl Waiter Chris Cook Max Helper Len 2

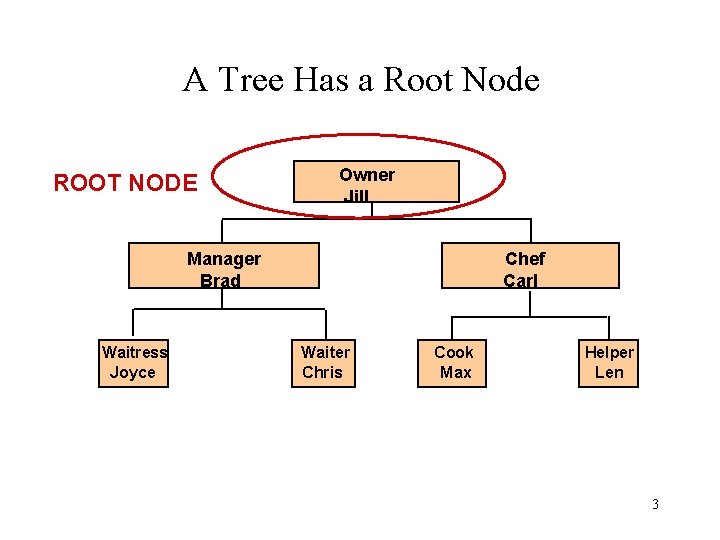
A Tree Has a Root Node ROOT NODE Owner Jill Manager Brad Waitress Joyce Chef Carl Waiter Chris Cook Max Helper Len 3

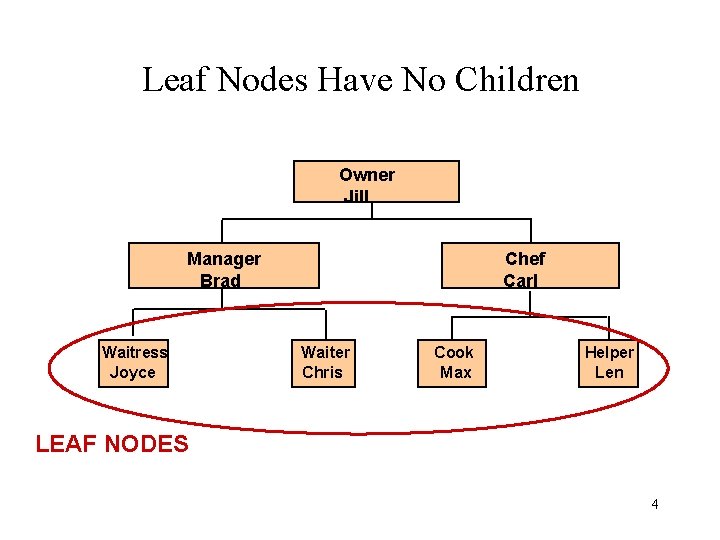
Leaf Nodes Have No Children Owner Jill Manager Brad Waitress Joyce Chef Carl Waiter Chris Cook Max Helper Len LEAF NODES 4

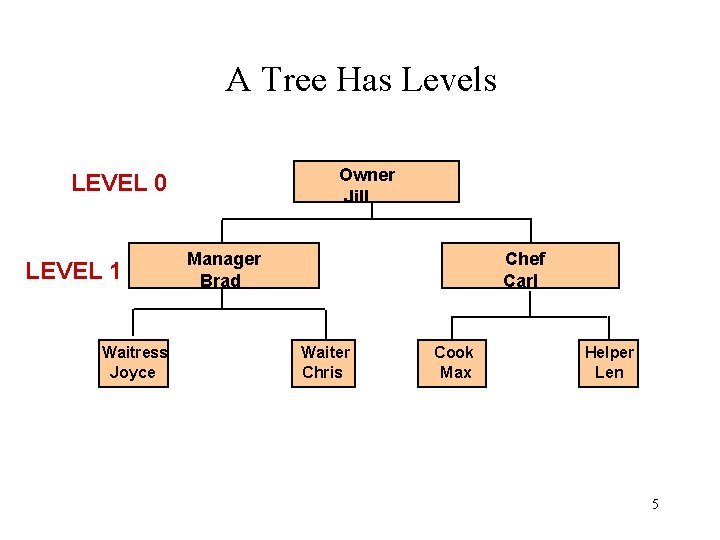
A Tree Has Levels Owner Jill LEVEL 0 LEVEL 1 Waitress Joyce Manager Brad Chef Carl Waiter Chris Cook Max Helper Len 5

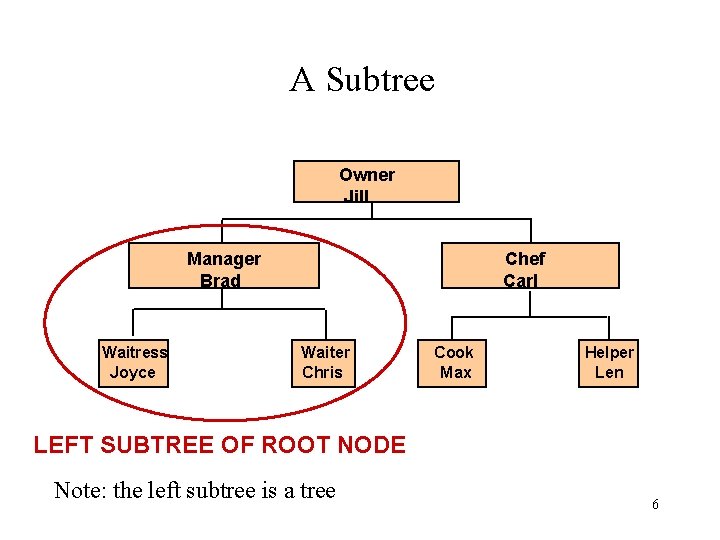
A Subtree Owner Jill Manager Brad Waitress Joyce Chef Carl Waiter Chris Cook Max Helper Len LEFT SUBTREE OF ROOT NODE Note: the left subtree is a tree 6

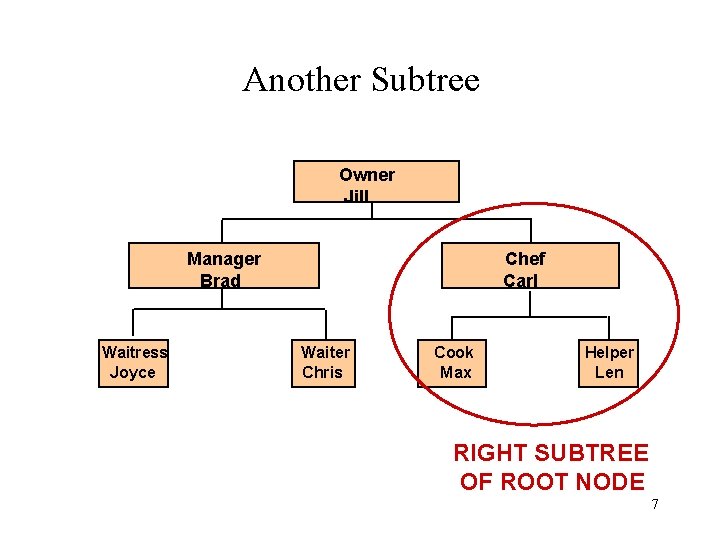
Another Subtree Owner Jill Manager Brad Waitress Joyce Chef Carl Waiter Chris Cook Max Helper Len RIGHT SUBTREE OF ROOT NODE 7

Binary Trees (formal definition) A binary tree, T, is either empty or such that – T has a special node called the root node – T has two sets of nodes: LT (the left subtreeof T) RT (the right subtree of T) – LT and RT are binary trees 8

Binary Tree Definitions Leaf: node that has no left and right children Parent: node with at least one child node Level of a node: number of steps from root to the node Height: number of nodes in the longest path from root to a leaf 9

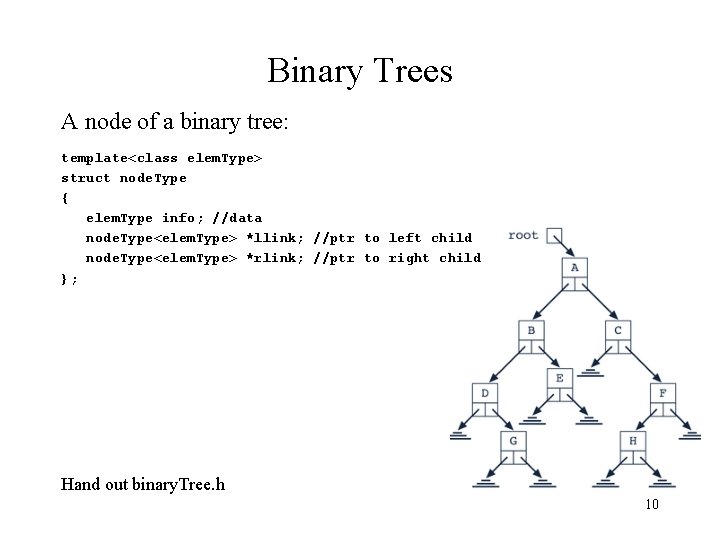
Binary Trees A node of a binary tree: template<class elem. Type> struct node. Type { elem. Type info; //data node. Type<elem. Type> *llink; //ptr to left child node. Type<elem. Type> *rlink; //ptr to right child }; Hand out binary. Tree. h 10

Height of a Binary Tree Recursive algorithm to find height of binary tree with root p: if(p is NULL) height(p) = 0 else height(p) = 1 + max(height(p->llink), height(p->rlink)) Recursive function: template<class elem. Type> int height(node. Type<elem. Type> *p) { if(p == NULL) return 0; else return 1 + max(height(p->llink), height(p->rlink)); } 11

Binary Tree Traversal Visit the root node first or visit the subtrees first – inorder • traverse the left subtree • visit the node • traverse the right subtree – preorder • visit the node • traverse the left subtree • traverse the right subtree – postorder • traverse the left subtree • traverse the right subtree • visit the node 12

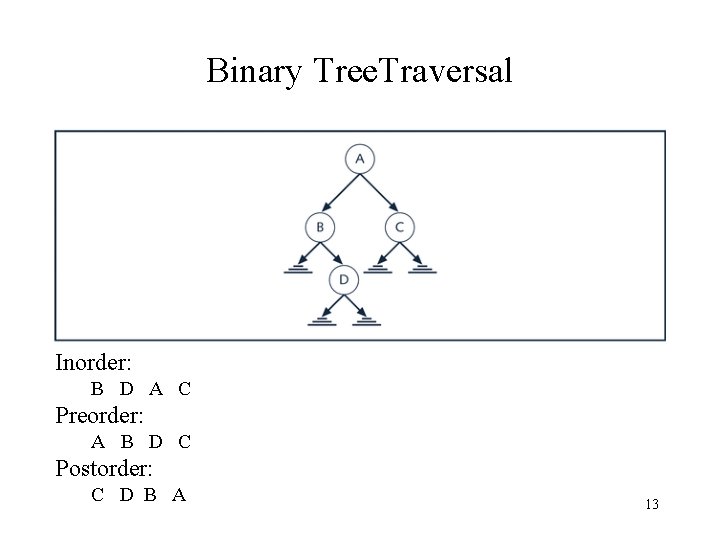
Binary Tree. Traversal Inorder: B D A C Preorder: A B D C Postorder: C D B A 13

Binary Tree: Traversals template<class elem. Type> void inorder(node. Type<elem. Type> *p) void postorder(node. Type<elem. Type> *p) { { if(p != NULL) { { inorder(p->llink); postorder(p->llink); cout<<p->info<<” “; postorder(p->rlink); inorder(p->rlink); cout<<p->info<<” “; } } }1 } What about preorder? 14

Traversal of Binary Expression Trees * a b What would be the effect of traversal inorder preorder postorder More later 15

A Binary Search Tree (BST) A special kind of binary tree in which: 1. each node contains a distinct data value, 2. the key values in the tree can be compared using “greater than” and “less than”, and 3. the key value of each node in the tree is less than every key value in its right subtree, and greater than every key value in its left subtree What would inorder traversal produce? 16

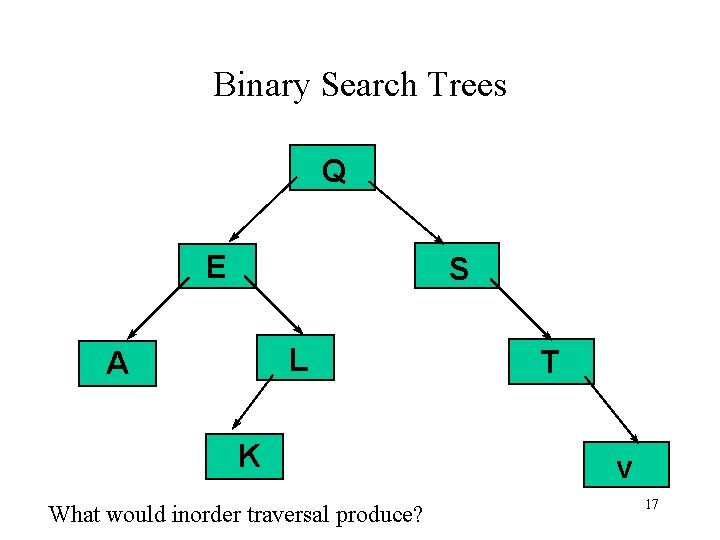
Binary Search Trees Q E S L A K What would inorder traversal produce? T v 17

Operations on Binary Search Trees Search for a particular item How do you know if 46 is in a tree? – is it the root? – no, less; – go left. . . 18

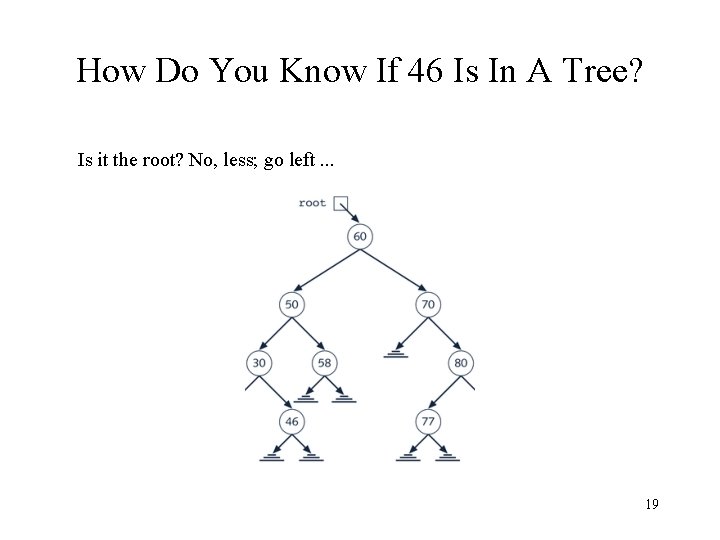
How Do You Know If 46 Is In A Tree? Is it the root? No, less; go left. . . 19

template<class elem. Type> bool b. Search. Tree. Type<elem. Type>: : search(const elem. Type& search. Item) { node. Type<elem. Type> *current; bool found = false; if(root == NULL) cerr<<"Cannot search the empty tree. "<<endl; else { current = root; while(current != NULL && !found) { if(current->info == search. Item) found = true; else if(current->info > search. Item) current = current->llink; else current = current->rlink; }//end while }//end else return found; }//end search Is there another way? 20

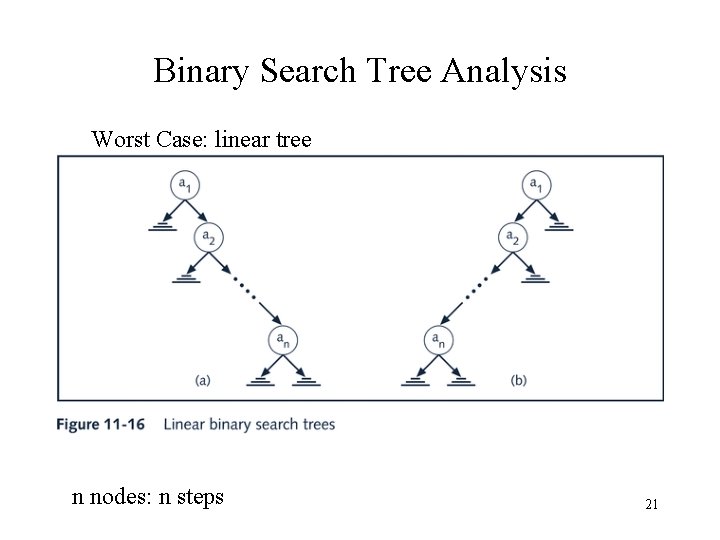
Binary Search Tree Analysis Worst Case: linear tree n nodes: n steps 21

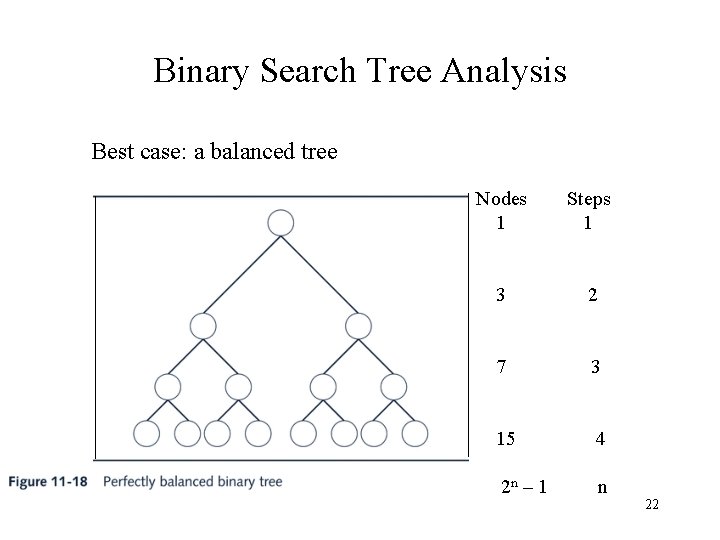
Binary Search Tree Analysis Best case: a balanced tree Nodes 1 Steps 1 3 2 7 3 15 4 2 n – 1 n 22

Creating Binary Search Tree Insert the elements ‘J’ ‘E’ ‘F’ ‘T’ ‘A’ in that order. Insert the first value into the root node: ‘J’ 23

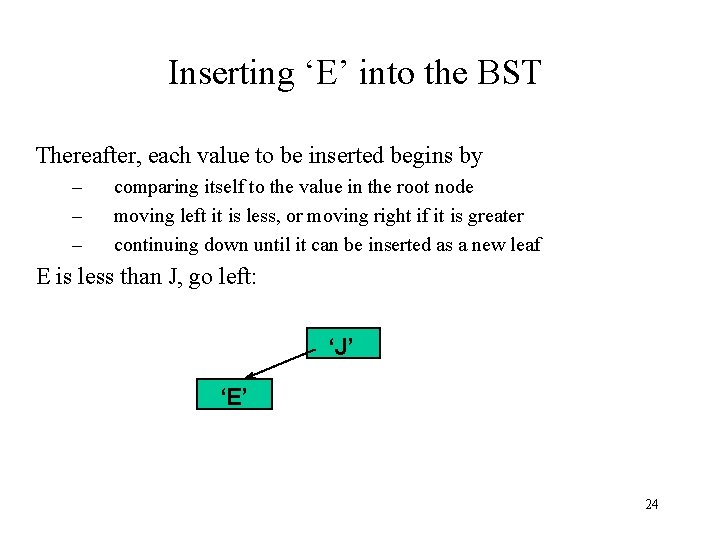
Inserting ‘E’ into the BST Thereafter, each value to be inserted begins by – – – comparing itself to the value in the root node moving left it is less, or moving right if it is greater continuing down until it can be inserted as a new leaf E is less than J, go left: ‘J’ ‘E’ 24

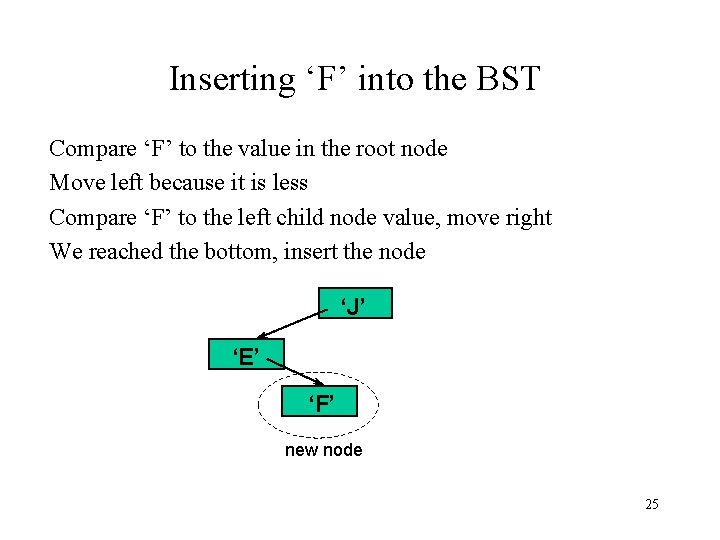
Inserting ‘F’ into the BST Compare ‘F’ to the value in the root node Move left because it is less Compare ‘F’ to the left child node value, move right We reached the bottom, insert the node ‘J’ ‘E’ ‘F’ new node 25

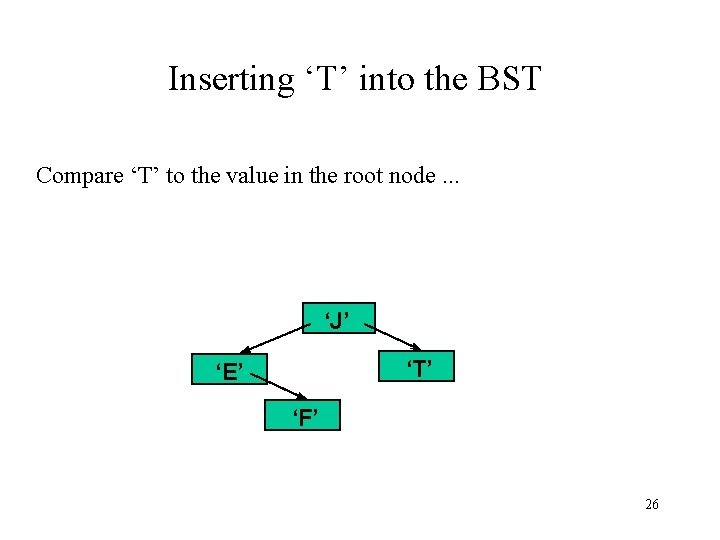
Inserting ‘T’ into the BST Compare ‘T’ to the value in the root node. . . ‘J’ ‘T’ ‘E’ ‘F’ 26

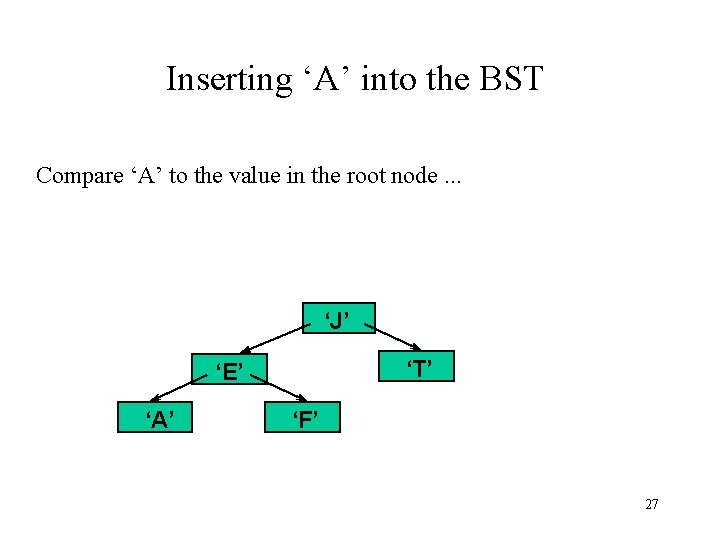
Inserting ‘A’ into the BST Compare ‘A’ to the value in the root node. . . ‘J’ ‘T’ ‘E’ ‘A’ ‘F’ 27

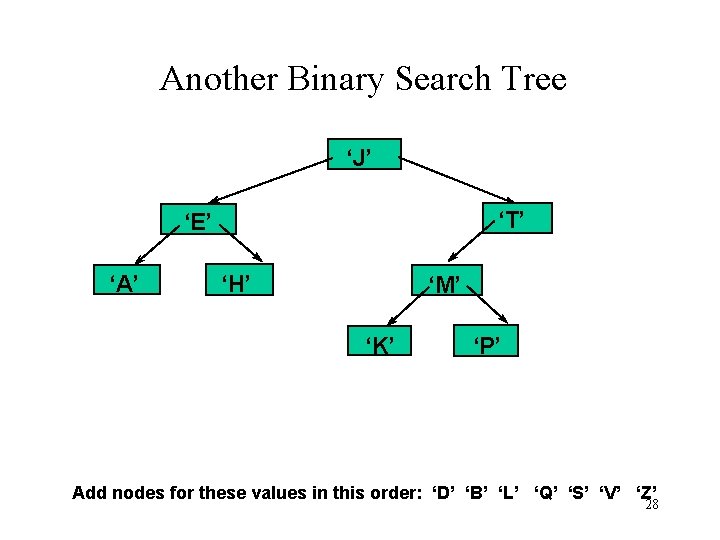
Another Binary Search Tree ‘J’ ‘T’ ‘E’ ‘A’ ‘H’ ‘M’ ‘K’ ‘P’ Add nodes for these values in this order: ‘D’ ‘B’ ‘L’ ‘Q’ ‘S’ ‘V’ ‘Z’ 28

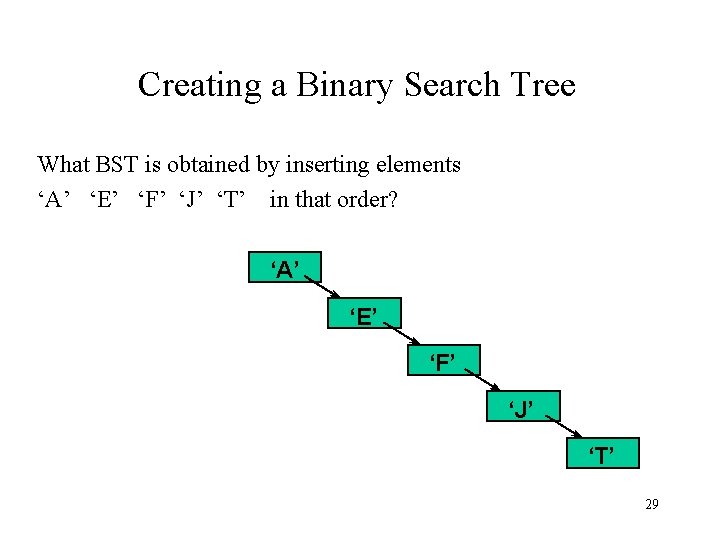
Creating a Binary Search Tree What BST is obtained by inserting elements ‘A’ ‘E’ ‘F’ ‘J’ ‘T’ in that order? ‘A’ ‘E’ ‘F’ ‘J’ ‘T’ 29

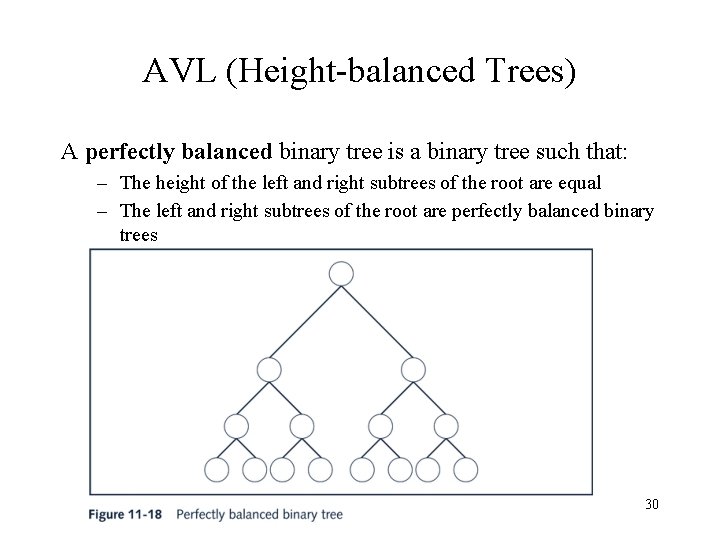
AVL (Height-balanced Trees) A perfectly balanced binary tree is a binary tree such that: – The height of the left and right subtrees of the root are equal – The left and right subtrees of the root are perfectly balanced binary trees 30

AVL (Height-balanced Trees) An AVL tree (or height-balanced tree) is a binary search tree such that: – the height of the left and right subtrees of the root differ by at most 1 – the left and right subtrees of the root are AVL trees Goal: maintain a BST as AVL Approach: rebalance unbalanced trees every now and then Us: skip this part 31

Full and Complete Binary Trees A full binary tree: all the leaves are on the same level and every non leaf node has two children. A complete binary tree: is either full or full through the nextto-last level, with the leaves on the last level as far to the left as possible. 32

Heaps A heap is a binary tree that satisfies special properties: – shape: a complete binary tree. – order: the value stored in each node is greater than or equal to the value in each of its children. Main applications: – heap sort – to implement a priority queue 33

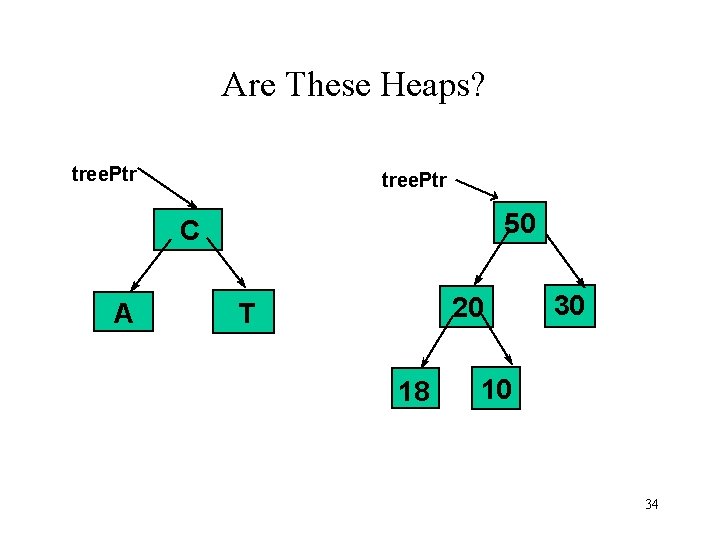
Are These Heaps? tree. Ptr 50 C A 20 T 18 30 10 34

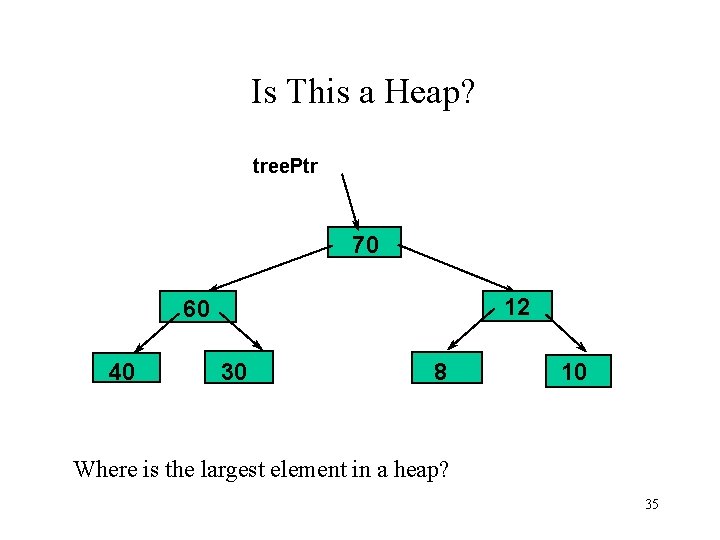
Is This a Heap? tree. Ptr 70 12 60 40 30 8 10 Where is the largest element in a heap? 35

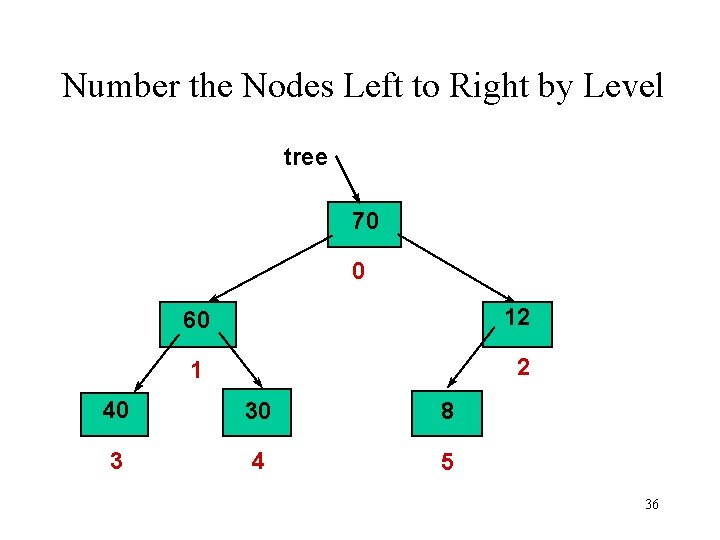
Number the Nodes Left to Right by Level tree 70 0 60 12 1 2 40 30 8 3 4 5 36

Use Node Numbers as Array Indexes tree. nodes [0] 70 [1] 60 [2] tree 70 0 12 60 12 1 2 [3] 40 [4] 30 40 30 6 [5] 6 3 4 5 [6] 37

Heap Sort for an Array 1. Make an unsorted array into a heap 2. Take the root (maximum) element off the heap by swapping it into its correct place in the array at the end of the unsorted elements 3. Reheap the remaining unsorted elements 4. Repeat until all elements are sorted 38

Reheap Down (Step 3) To make heaps when all but the top element is in heap position How: – swap root with left or right child, which ever violates heapness – reheap (down) with that child Used when application wants to remove the highest element: – remove the root – put last element in root position – reheap down to restore the order 39

Create the Original Heap (how later) values [0] 70 [1] 60 [2] root 70 0 12 60 12 1 2 [3] 40 [4] 30 40 30 6 10 [5] 6 3 4 5 6 [6] 10 40

Swap Root Element int last Place in Unsorted Array values [0] 70 [1] 60 [2] root 70 0 12 60 12 1 2 [3] 40 [4] 30 40 30 6 10 [5] 6 3 4 5 6 [6] 10 41

After Swapping Root Element values [0] 10 [1] 60 [2] root 10 0 12 60 12 1 2 [3] 40 [4] 30 40 30 6 70 [5] 6 3 4 5 6 [6] 70 This is in the right slot No need to consider again 42

The Unsorted Array Is No Longer A Heap values [0] 10 [1] 60 [2] root 10 0 12 60 12 1 2 [3] 40 [4] 30 40 30 6 [5] 6 3 4 5 10 is out of place, swap with its largest child 60 10 is out of place, swap with its largest child 40 43

Remaining Unsorted Elements Reheaped: values [0] 60 [1] 40 [2] root 60 0 12 40 12 1 2 [3] 10 [4] 30 10 30 6 70 [5] 6 3 4 5 6 [6] 70 44

Swap Root Element Into Last Unsorted Place values [0] 60 [1] 40 [2] root 60 0 12 40 12 1 2 [3] 10 [4] 30 10 30 [5] 6 3 4 [6] 70 6 5 70 6 45

After Swapping Root Element values [0] 6 [1] 40 [2] root 6 0 12 40 12 1 2 [3] 10 [4] 30 10 30 60 70 [5] 60 3 4 5 6 [6] 70 In the right slots No need to consider again 46

Reheap Remaining Unsorted Elements values [0] 40 [1] 30 [2] root 40 0 12 30 12 1 2 [3] 10 [4] 6 10 6 60 70 [5] 60 3 4 5 6 [6] 70 47

Swap Root Element Into Last Unsorted Place values [0] 40 [1] 30 [2] root 40 0 12 30 12 1 2 [3] 10 [4] 6 10 6 60 70 [5] 60 3 4 5 6 [6] 70 48

After Swapping Root Element values [0] 6 [1] 30 [2] root 6 0 12 30 12 1 2 [3] 10 [4] 40 10 40 60 70 [5] 60 3 4 5 6 [6] 70 In the right slots No need to consider again 49

Reheap Remaining Unsorted Elements values [0] 30 [1] 10 [2] root 30 0 12 1 2 [3] 6 [4] 40 60 70 [5] 60 3 4 5 6 [6] 70 50

Swap Root Element Into Last Unsorted Place values [0] 30 [1] 10 [2] root 30 0 12 1 2 [3] 6 [4] 40 60 70 [5] 60 3 4 5 6 [6] 70 51

After Swapping Root Element values [0] 6 [1] 10 [2] root 6 0 12 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 In the right slots No need to consider again 52

After Reheaping Remaining Unsorted Elements values [0] 12 [1] 10 [2] root 12 0 6 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 53

Swap Root Element Into Last Unsorted Place values [0] 12 [1] 10 [2] root 12 0 6 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 54

After Swapping Root Element values [0] 6 [1] 10 [2] root 6 0 12 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 In the right slots No need to consider again 55

After Reheaping Remaining Unsorted Elements values [0] 10 [1] 6 [2] root 10 0 12 6 12 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 56

Swap Root Element Into Last Unsorted Place values [0] 10 [1] 6 [2] root 10 0 12 6 12 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 57

After Swapping Root Element values [0] 6 [1] 10 [2] root 6 0 12 1 2 [3] 30 [4] 40 30 40 60 70 [5] 60 3 4 5 6 [6] 70 All elements are sorted 58

Implementing Heaps Text approach – add function to ordered. Array. List. Type to build a heap – add function to ordered. Array. List. Type for heap sort Comment: – this is counterintuitive – a heap is not an ordered array A different approach – define a heap struct – include functions for converting an array to a heap – use the heap struct to build heap sort 59

// HEAP SPECIFICATION // Assumes Item. Type is either a built-in simple data type // or a class with overloaded relational operators. template< class Item. Type > struct Heap. Type { void Reheap. Down ( int root , int bottom ) ; void Reheap. Up ( int root, int bottom ) ; Item. Type* elements ; // ARRAY to be allocated dynamically int num. Elements ; }; 60 60

Observations Heap is a struct with member functions Why not a class? – to allow access to its components – heaps are usually used in conjunction with other classes which want access to the components but will hide the components from the application using them 61

Reheap Down Make a heap when all but the top element is in heap position How: – swap root with left or right child, whicheever violates heapness – reheap (down) with that child Used to put the highest element is its sorted position: – remove the root – put last element in root position – reheap down to restore the order 62

Reheap Up (slide differs from notes) For a node that violates a heap upwards: swap with parent until it is a heap So, if we add a node to the “end” of the tree that is otherwise a heap, reheap up would put it in the right spot Build a heap method 1: – start with empty heap – add element to the end and reheap up Build a heap method 2 (in heapsort. h): – – reheap down with the parent of the last child reheap down with the element before that. . . reheap down with node 0 63

Back to Heapsort This does not use the heap struct It adds the array to be sorted as a parameter to Reheap. Down: template<class elem. Type> void heap. Sort(elem. Type values[], int num. Values) { // Convert the array of values into a heap. // Sort the array. } 64

template <class Item. Type > void Heap. Sort ( Item. Type values [ ] , int num. Values ) // Post: Sorts array values[ 0. . num. Values-1 ] into // ascending order by key { int index ; // Convert array values[0. . num. Values-1] into a heap for (index = num. Values/2 - 1; index >= 0; index--) Reheap. Down ( values , index , num. Values - 1 ) ; } // Sort the array. for (index = num. Values - 1; index >= 1; { Swap (values [0] , values[index]); Reheap. Down (values , 0 , index - 1); } index--) Alternate way to convert values[0. . num. Values-1] for (index =1; num. Values-1; index++) Reheap. Up ( values , 0 , index ) ; into a heap: 65 65

Exercises Make a heap out of elements DHAKPR Remove the top element and reheap 66

Priority Queues An ADT with the property that only the highest-priority element can be accessed at any time Example: homework assignments are ordered by priority Like a sorted list except for the access restriction Goal: be able to insert in order and to access the top element efficiently Approach: use a heap Notation: Enqueue = = add. Queue Dequeue = = remove and return the removed item (combines front and delete. Queue) 67

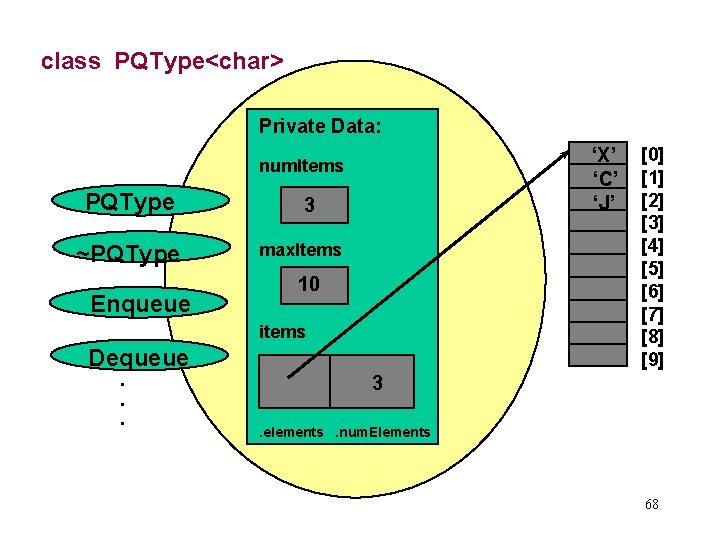
class PQType<char> Private Data: ‘X’ ‘C’ ‘J’ num. Items PQType ~PQType Enqueue 3 max. Items 10 items Dequeue. . . [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] 3. elements. num. Elements 68

// CLASS PQTYPE DEFINITION AND MEMBER FUNCTIONS //--------------------------template<class Item. Type> class PQType { public: PQType( int ); ~PQType ( ); void Make. Empty( ); bool Is. Empty( ) const; bool Is. Full( ) const; void Enqueue( elem. Type item ); //adds a new item void Dequeue( elem. Type& item ); //returns the removed item private: int num. Items; heap. Type<elem. Type> int max. Items; }; items; See driver code on website 69 69

Priority Queues: enqueue Assuming the priority queue is implemented as a heap, insert the new element in the next position in the list and reheap up template<class elem. Type> void PQType<elem. Type>: : Enqueue(elem. Type new. Item) { num. Items++; items. elements[num. Items - 1] = new. Item; items. Reheap. Up(0, num. Items - 1); } 70

Priority Queues: dequeue Assume the priority queue is implemented as a heap To remove the first element of the priority queue: copy the last element of the list into the first array position. reduce the length of the list by 1. Reheap. Up to restore the heap in the list template<class elem. Type> void PQType<elem. Type>: : Dequeue(elem. Type& item) { item = items. elements[0]; //the value items. elements[0] = items. elements[num. Items-1]; num. Items--; items. Reheap. Down(0, num. Items - 1); } returned //1 //2 //3 71

A Binary Expression Tree is. . . A special kind of binary tree in which: 1. each leaf node contains a single operand 2. each nonleaf node contains a single binary 3. the left and right subtrees of an operator node represent subexpressions that must be evaluated before applying the operator 72

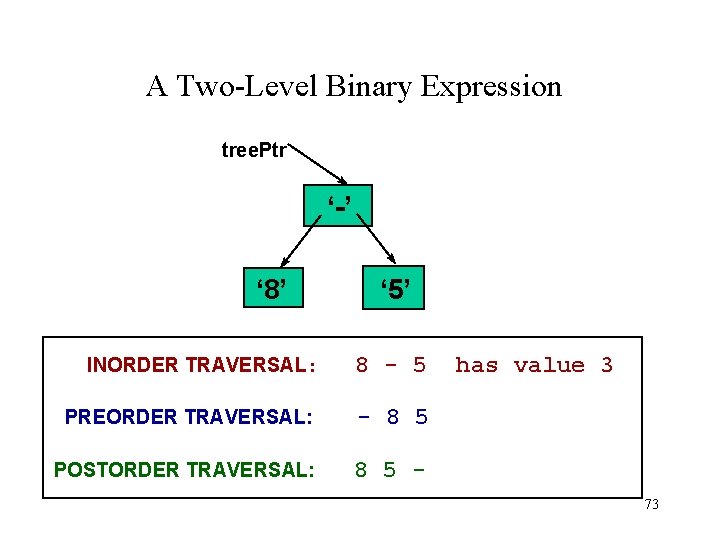
A Two-Level Binary Expression tree. Ptr ‘-’ ‘ 8’ INORDER TRAVERSAL: ‘ 5’ 8 - 5 PREORDER TRAVERSAL: - 8 5 POSTORDER TRAVERSAL: 8 5 - has value 3 73

Levels Indicate Precedence When a binary expression tree represents an expression, the levels of the nodes in the tree indicate their relative precedence of evaluation Operations at higher levels of the tree are evaluated later than those below them The root operation is always performed last 74

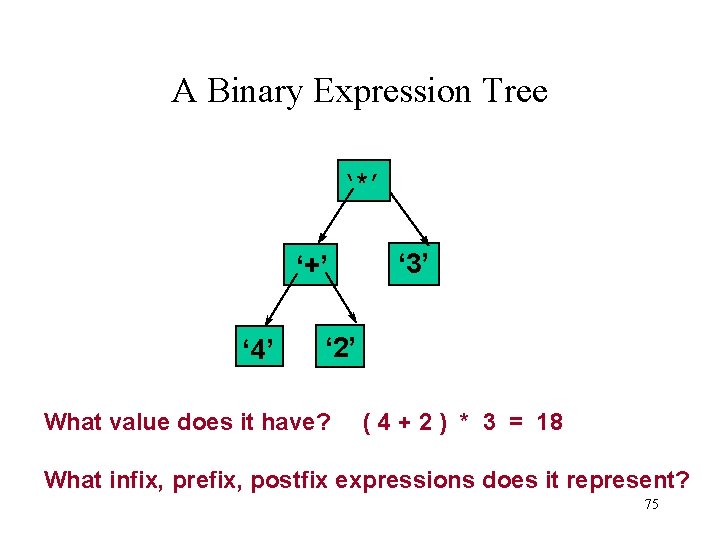
A Binary Expression Tree ‘*’ ‘+’ ‘ 4’ ‘ 3’ ‘ 2’ What value does it have? ( 4 + 2 ) * 3 = 18 What infix, prefix, postfix expressions does it represent? 75

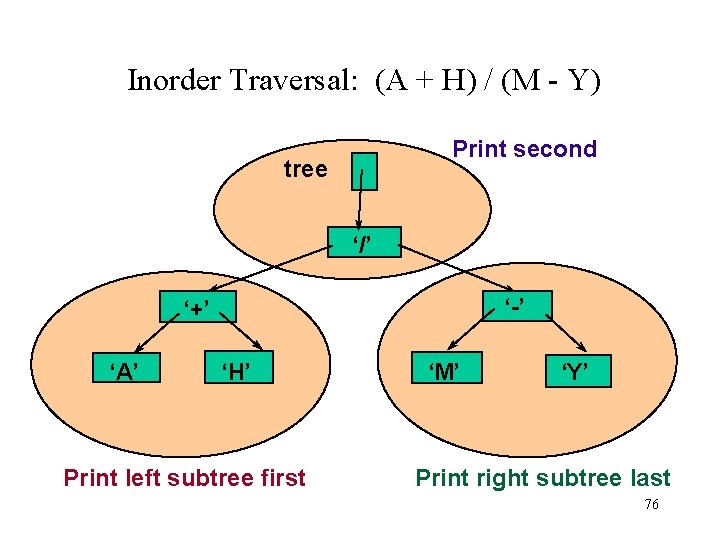
Inorder Traversal: (A + H) / (M - Y) Print second tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree last 76

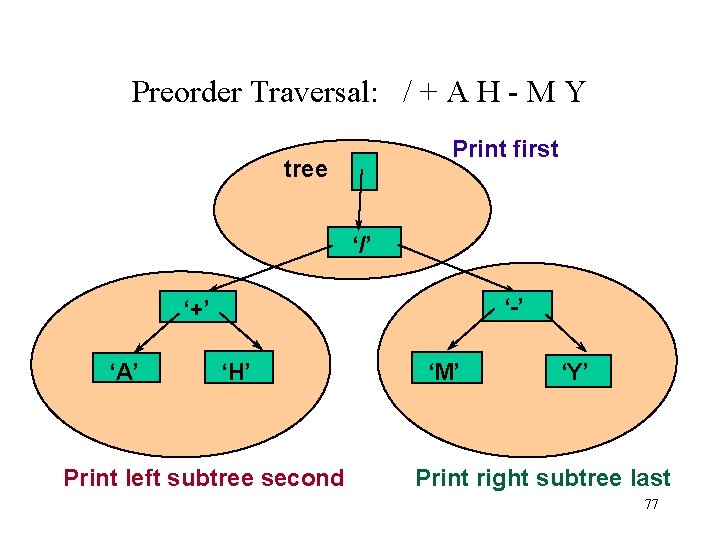
Preorder Traversal: / + A H - M Y Print first tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree second ‘M’ ‘Y’ Print right subtree last 77

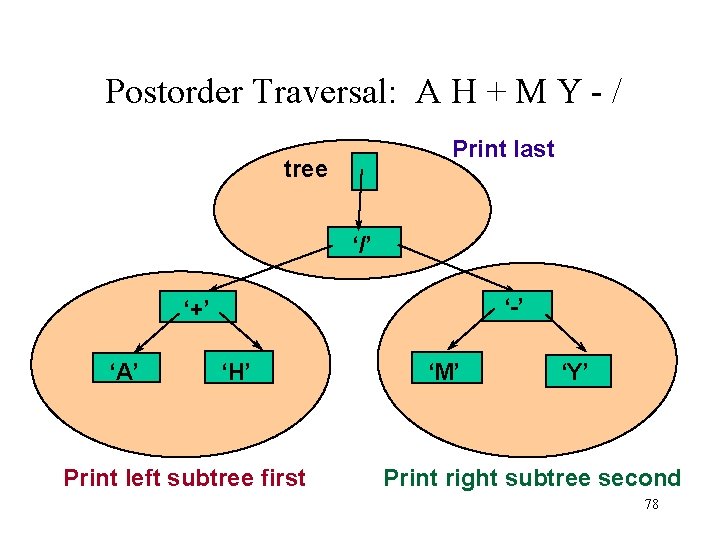
Postorder Traversal: A H + M Y - / Print last tree ‘/’ ‘-’ ‘+’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree second 78

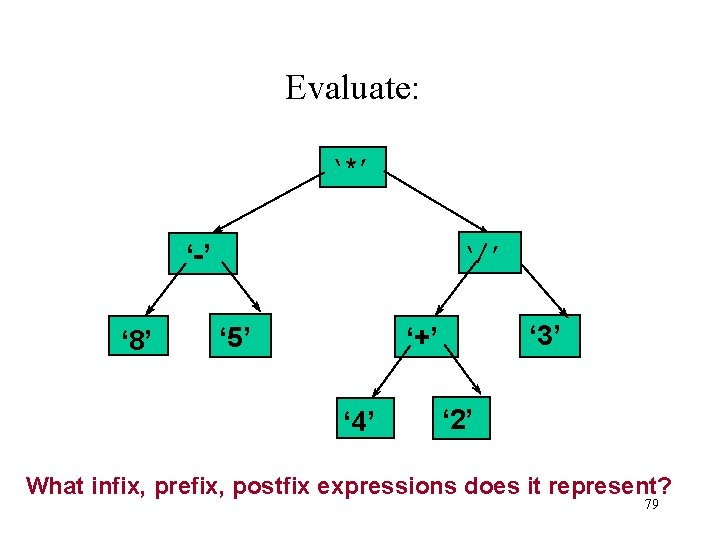
Evaluate: ‘*’ ‘-’ ‘ 8’ ‘/’ ‘ 5’ ‘ 3’ ‘+’ ‘ 4’ ‘ 2’ What infix, prefix, postfix expressions does it represent? 79

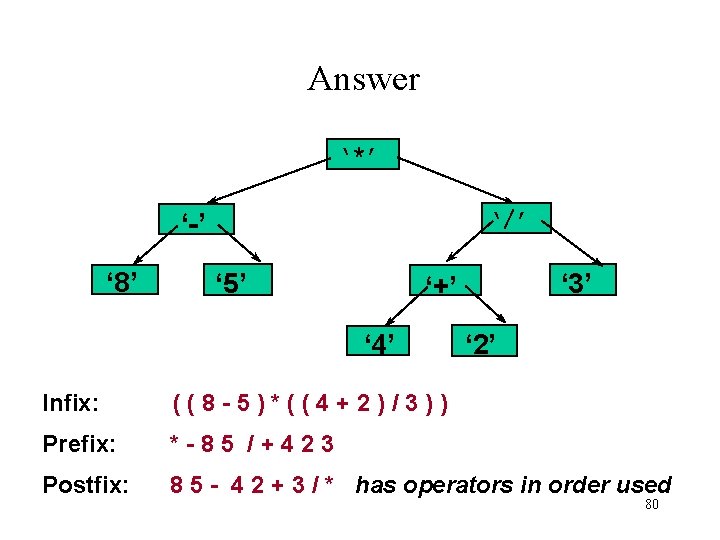
Answer ‘*’ ‘/’ ‘-’ ‘ 8’ ‘ 5’ ‘ 3’ ‘+’ ‘ 4’ ‘ 2’ Infix: ((8 -5)*((4+2)/3)) Prefix: *-85 /+423 Postfix: 8 5 - 4 2 + 3 / * has operators in order used 80

The Content in a Tree Nodes has 2 forms enum Op. Type struct { OPERATOR, elem. Type OPERAND } ; { Op. Type which. Type; union // content dependes on the value of which. Type { char operation ; int operand ; } }; OPERATOR. which. Type ‘+’. operation OPERAND. which. Type 7 . operand 81

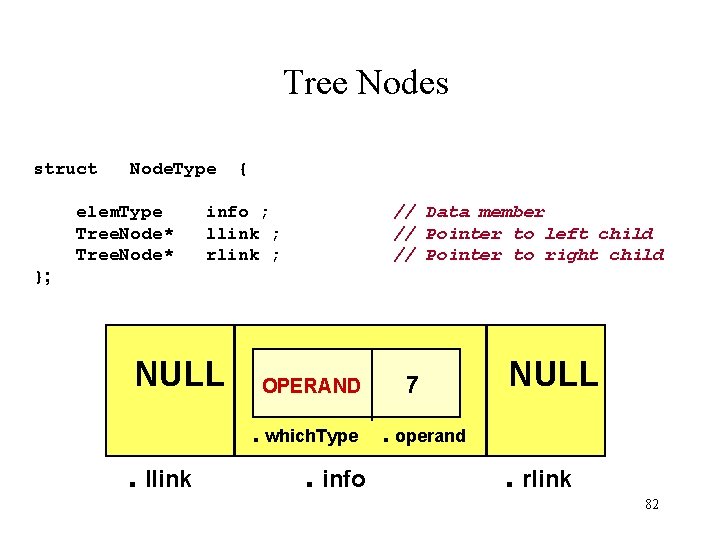
Tree Nodes struct Node. Type elem. Type Tree. Node* { info ; llink ; rlink ; // Data member // Pointer to left child // Pointer to right child }; NULL OPERAND. which. Type . llink . info 7 NULL . operand . rlink 82

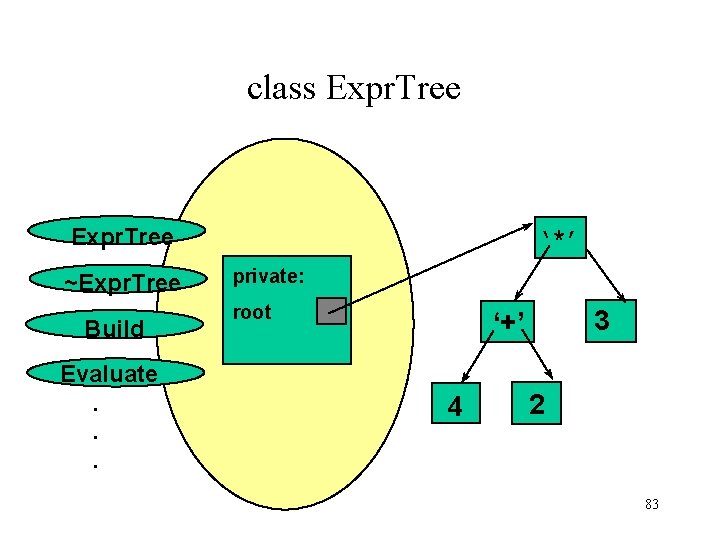
class Expr. Tree ~Expr. Tree Build Evaluate. . . ‘*’ private: root 3 ‘+’ 4 2 83

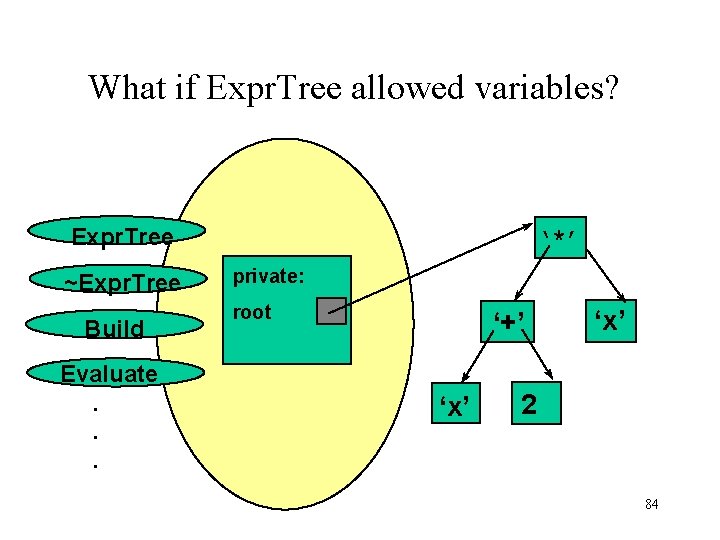
What if Expr. Tree allowed variables? Expr. Tree ~Expr. Tree Build Evaluate. . . ‘*’ private: root ‘+’ ‘x’ 2 84

What Can You Do With This? Add VARIABLE to enumerated type Operand Evaluate a function? int Eval ( Tree. Node* ptr, float value ). . . case VARIABLE return value Differentiate a function? 85