CS 123 INTRODUCTION TO COMPUTER GRAPHICS Scan Conversion

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Scan Conversion CS 123 Andries van Dam© 10/15/2019 1/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Scan Converting Lines Line Drawing � First problem statement: Draw a line on a raster screen between two points � Why is this a difficult problem? � � � What is “drawing” on a raster display? What is a “line” in raster world? Efficiency and appearance are both important Problem Statement � Given two points P and Q in the XY plane, both with integer coordinates, determine which pixels on a raster screen should be drawn in order to best approximate a unit-width line segment starting at P and ending at Q Andries van Dam© 10/15/2019 2/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS What is Scan Conversion? Final step of rasterization (the process of taking geometric shapes and converting them into an array of pixels stored in the framebuffer to be displayed) – converting from “random scan”/vector specification to a raster scan where we specify which pixels are drawn based on a stored array of primitives. � Takes place after clipping occurs � All graphics packages do this at end of the rendering pipeline � Takes triangles (or higher-order primitives) and maps them to pixels on screen � For 3 D: rendering also takes into account other processes, like lighting and shading, but we’ll focus first on algorithms for line scan conversion � Andries van Dam© 10/15/2019 3/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Scan-converting a Line: Finding the next pixel Special cases: � Horizontal Line: � Draw pixel P and increment x coordinate value by 1 to get next pixel. Vertical Line: � Draw pixel P and increment y coordinate value by 1 to get next pixel. Diagonal Line: � Draw pixel P and increment both x and y coordinate by 1 to get next pixel. What should we do in the general case? � � � For slope <= 1, increment x coordinate by 1 and choose pixel on or closest to line. Slopes in other octants by reflection (e. g. , in second octant, increment Y) But how do we measure “closest”? Andries van Dam© 10/15/2019 4/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Vertical Distance Why can we use vertical distance as a measure of which point (pixel center) is closer? � Similar triangles show that true distances to line (in blue) are directly proportional to vertical distances to line (in black) for each point � Therefore, point with smaller vertical distance to line is closest to line � Andries van Dam© 10/15/2019 5/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Clicker Andries van Dam© 10/15/2019 6/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Vertical Distance Basic Algorithm: � Find equation of line that connects points P and Q � Draw pixel P and increment x coordinate value by 1 to get next pixel. Vertical Line: � Draw pixel P and increment y coordinate value by 1 to get next pixel. Diagonal Line: � Draw pixel P and increment both x and y coordinate by 1 to get next pixel. What should we do in the general case? � � � For slope <= 1, increment x coordinate by 1 and choose pixel on or closest to line. Slopes in other octants by reflection (e. g. , in second octant, increment Y) Use vertical distance to measure “closest” Andries van Dam© 10/15/2019 7/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 1 – Incremental Algorithm (1/3) � Andries van Dam© 10/15/2019 8/48

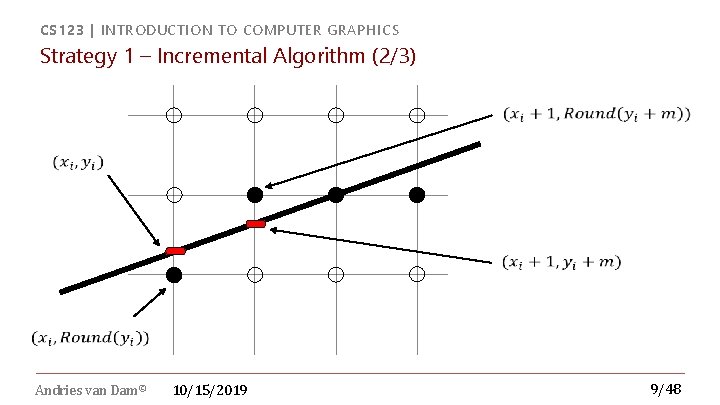
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 1 – Incremental Algorithm (2/3) Andries van Dam© 10/15/2019 9/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 1 – Incremental Algorithm (3/3) - Issues void Line(int x 0, int x, y; float dy = y 1 float dx = x 1 float m = dy int y 0, int x 1, int y 1) { – y 0; – x 0; / dx; y = y 0; for (x = x 0; x < x 1; ++x) { Write. Pixel( x, Round(y) ); y = y + m; Since slope is fractional, need special case for vertical lines (dx = 0) Rounding takes time } } Andries van Dam© 10/15/2019 10/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 2 – Midpoint Line Algorithm (1/3) � Andries van Dam© 10/15/2019 11/48

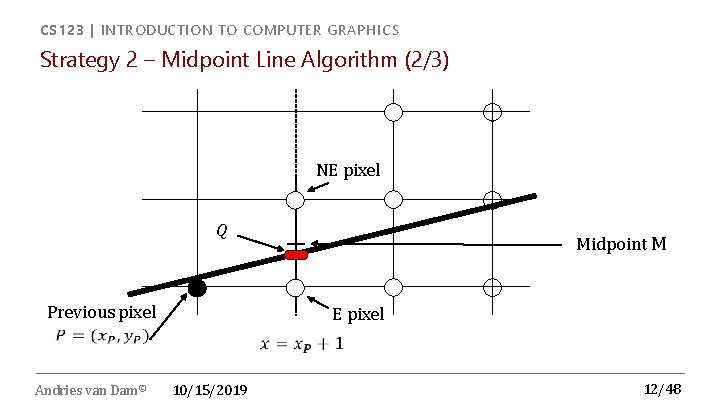
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 2 – Midpoint Line Algorithm (2/3) NE pixel Q Previous pixel Andries van Dam© Midpoint M E pixel 10/15/2019 12/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Clicker Andries van Dam© 10/15/2019 13/48

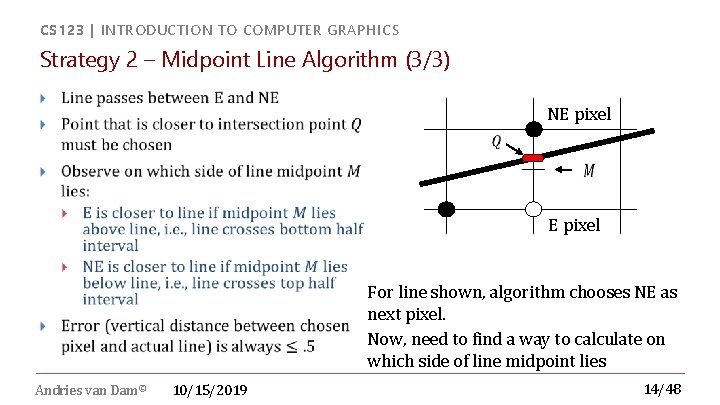
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Strategy 2 – Midpoint Line Algorithm (3/3) NE pixel For line shown, algorithm chooses NE as next pixel. Now, need to find a way to calculate on which side of line midpoint lies Andries van Dam© 10/15/2019 14/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS General Line Equation in Implicit Form � Andries van Dam© 10/15/2019 15/48

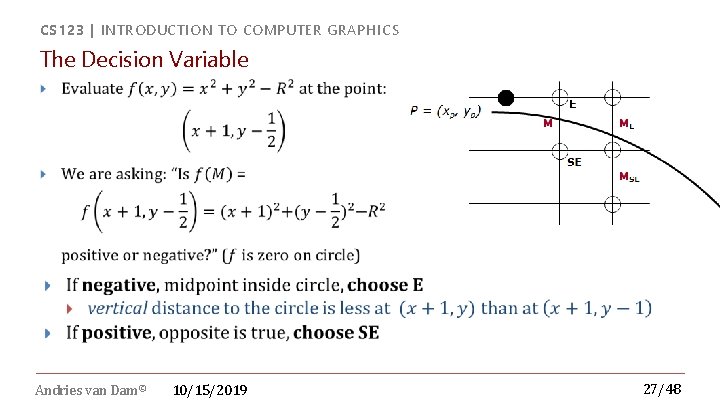
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Decision Variable � Andries van Dam© 10/15/2019 16/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Incrementing Decision Variable if E was chosen: � Andries van Dam© 10/15/2019 17/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS If NE was chosen: � Andries van Dam© 10/15/2019 18/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Summary (1/2) � Andries van Dam© 10/15/2019 19/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Summary (2/2) � Andries van Dam© 10/15/2019 20/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Example Code void Midpoint. Line(int x 0, int y 0, int x 1, int y 1) { int dx = (x 1 - x 0), dy = (y 1 - y 0); int d = 2 * dy - dx; int incr. E = 2 * dy; int incr. NE = 2 * (dy - dx); int x = x 0, y = y 0; Write. Pixel(x, y); } while (x < x 1) { if (d <= 0) d = d + incr. E; // East Case else { d = d + incr. NE; ++y; } // Northeast Case ++x; Write. Pixel(x, y); } Andries van Dam© 10/15/2019 21/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Scan Converting Circles (0, 17) (17, 0) Andries van Dam© 10/15/2019 22/48

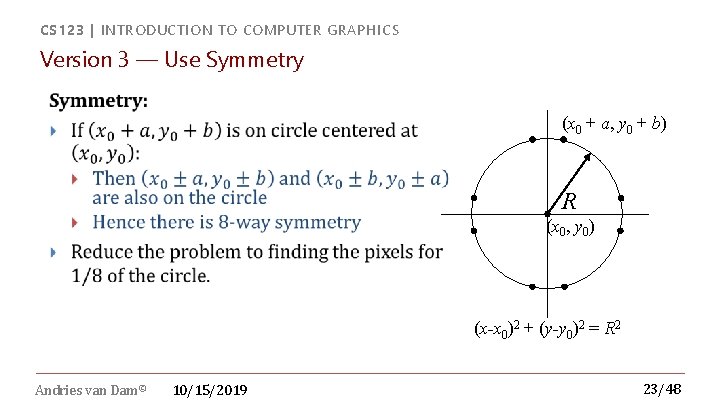
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Version 3 — Use Symmetry (x 0 + a, y 0 + b) R (x 0, y 0) (x-x 0)2 + (y-y 0)2 = R 2 Andries van Dam© 10/15/2019 23/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Using the Symmetry (x 0, y 0) Andries van Dam© 10/15/2019 24/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS The Incremental Algorithm – a Pseudocode Sketch Clicker A. B. C. D. Andries van Dam© 10/15/2019 (1) Southeast, (2) East (1) West, (2) Southwest (1) East, (2) Southeast (1) East, (2) East 25/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS What we need for the Incremental Algorithm Andries van Dam© 10/15/2019 26/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS The Decision Variable Andries van Dam© 10/15/2019 27/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS The right decision variable? Andries van Dam© 10/15/2019 28/48

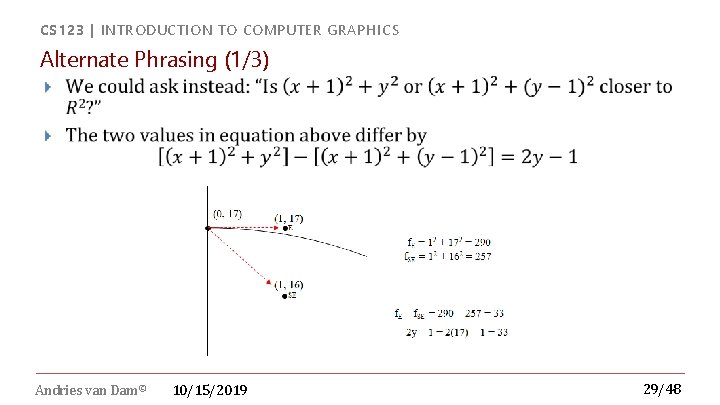
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Alternate Phrasing (1/3) Andries van Dam© 10/15/2019 29/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Alternate Phrasing (2/3) Andries van Dam© 10/15/2019 30/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Alternate Phrasing (3/3) Andries van Dam© 10/15/2019 31/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Incremental Computation Revisited (1/2) Andries van Dam© 10/15/2019 32/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Incremental Computation (2/2) Andries van Dam© 10/15/2019 33/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Second Differences (1/2) Andries van Dam© 10/15/2019 34/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Second Differences (2/2) Andries van Dam© 10/15/2019 35/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Midpoint Eighth Circle Algorithm Midpoint. Eighth. Circle(R) { /* 1/8 th of a circle w/ radius R */ int x = 0, y = R; int delta. E = 2 * x + 3; int delta. SE = 2 * (x - y) + 5; float decision = (x + 1) * (x + 1) + (y - 0. 5) * (y - 0. 5) – R*R; Write. Pixel(x, y); } while ( y > x ) { if (decision > 0) { // Move x++; Write. Pixel(x, y); decision += delta. E; delta. E += 2; delta. SE += } else { // Move South. East y--; x++; Write. Pixel(x, decision += delta. SE; delta. E += 2; delta. SE += } } Andries van Dam© 10/15/2019 East 2; // Update deltas y); 4; // Update deltas 36/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Analysis � Uses floats! � 1 test, 3 or 4 additions per pixel � Initialization can be improved � Multiply everything by 4: No floats! � Makes the components even, but sign of decision variable remains same Questions � Are we getting all pixels whose distance from the circle is less than ½? � Why is y > x the right criterion? � What if it were an ellipse? Andries van Dam© 10/15/2019 37/48

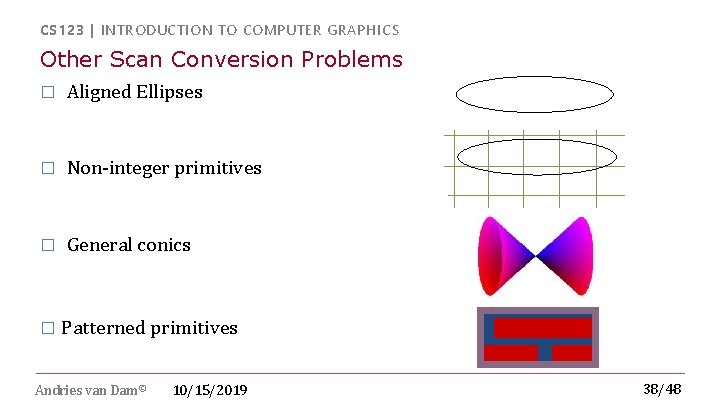
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Other Scan Conversion Problems � Aligned Ellipses � Non-integer primitives � General conics � Patterned primitives Andries van Dam© 10/15/2019 38/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Aligned Ellipses Andries van Dam© 10/15/2019 39/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Direction Changing Criterion (1/2) Andries van Dam© 10/15/2019 40/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Direction Changing Criterion (2/2) Andries van Dam© 10/15/2019 41/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Problems with aligned ellipses � � Now in ENE octant, not ESE octant. Used the wrong direction because the ellipse rapidly changes slope within a pixel This problem is an artifact of aliasing, remember filter? Andries van Dam© 10/15/2019 42/48

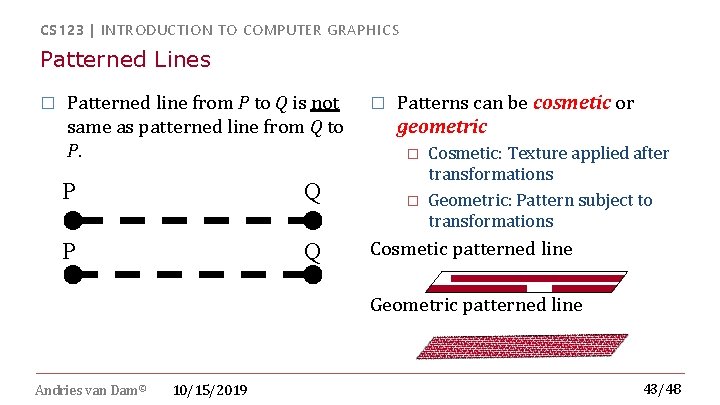
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Patterned Lines � Patterned line from P to Q is not same as patterned line from Q to P. P Q � Patterns can be cosmetic or geometric � � Cosmetic: Texture applied after transformations Geometric: Pattern subject to transformations Cosmetic patterned line Geometric patterned line Andries van Dam© 10/15/2019 43/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Geometric vs. Cosmetic + Cosmetic (Real-World Contact Paper) Geometric (Perspectivized/Filtered) Andries van Dam© 10/15/2019 44/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Non-Integer Primitives and General Conics Andries van Dam© 10/15/2019 45/48

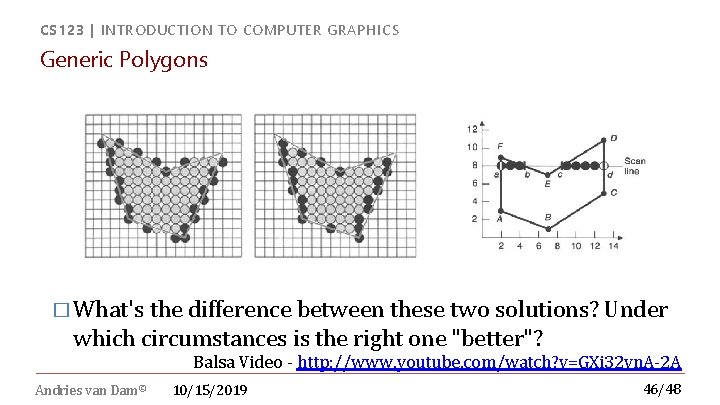
CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Generic Polygons � What's the difference between these two solutions? Under which circumstances is the right one "better"? Balsa Video - http: //www. youtube. com/watch? v=GXi 32 vn. A-2 A Andries van Dam© 10/15/2019 46/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Notes on Two Techniques � Forward differences should remind you of finite differences used in calculus to approximate derivatives (Δy/Δx -> dy/dx as Δx -> 0) � Δy is calculated the same way as f(x + Δx) – f(x) � for polynomials they are one degree lower � The odd parity rule for filling in pixel spans between edges is used for “point in polygon” tests, e. g. , for “pick correlation” of shapes) � “point in rectangle” test, e. g. , using upright bounding box is first-order approximation that just does bounds testing � shoot a ray at any angle and count parity of intersections for actual polygons or (piecewise) curved boundaries � intersections with shared vertices are special-cased Andries van Dam© 10/15/2019 47/48

CS 123 | INTRODUCTION TO COMPUTER GRAPHICS Scan Converting Arbitrary Solids � Rapid Prototyping is becoming cheaper and more prevalent � 3 D printers use various methods to print rasterized slices of whole solid objects � � � Extrude layer after layer of material from a nozzle (Makerbot) Use UV light to cure material from a liquid bath (Formlabs) Use heat to cure material from powdered materials (3 D Systems) And more! http: //3 dprintingindustry. com/3 d-printing-basics-free-beginnersguide/processes/ We have an RP lab across the street in Barus and Holley There also a couple printers in the Io. T lab (8 th floor of the Sci-Li) Prosthetics - https: //youtu. be/ip. P-z_ko. TZs � Food! - https: //youtu. be/Gh 99 f. XAwmi 4? t=17 � Andries van Dam© 10/15/2019 48/48