CS 1120 Recursion 1 What is Recursion n

CS 1120: Recursion 1

What is Recursion? n n A method is said to be recursive if the method definition contains a call to itself A recursive method is a method that calls itself method A (…) 2

Why Recursion? n n In pursuit of absolute simplicity!!! An important idea behind recursion is to Divide, Conquer, and Glue (DCG) n n n Divide the Problem P into subproblems P 1, P 2, …, Pn Conquer the subproblem by solving them S 1, S 2, …, Sn Glue subsolutions S 1, S 2, …, Sn together into the solution S to the whole problem. 3

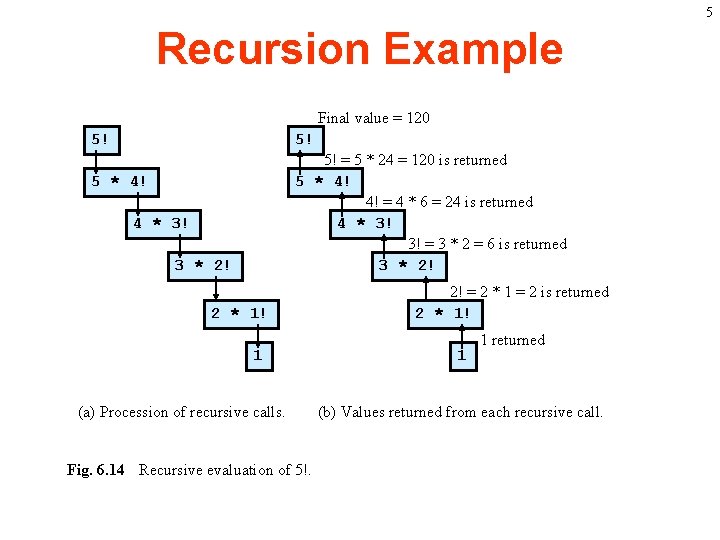
4 Example of Recursion • Often these subtasks are similar, but get smaller in size. Next, we further break these subtasks into sub-subtasks until the sub-subtasks cannot be further broken. – For example, factorial(3) can be calculated if factorial(2) can be calculated if factorial(1) can be calculated. factorial(1) is not further broken since everyone know it is 1!!!

5 Recursion Example Final value = 120 5! 5! 5! = 5 * 24 = 120 is returned 5 * 4! 4! = 4 * 6 = 24 is returned 4 * 3! 3! = 3 * 2 = 6 is returned 3 * 2! 5 * 4! 4 * 3! 3 * 2! 2 * 1! 1 (a) Procession of recursive calls. Fig. 6. 14 Recursive evaluation of 5!. 2! = 2 * 1 = 2 is returned 2 * 1! 1 1 returned (b) Values returned from each recursive call.

Some Terminology n Base Case: the simplest case n n In factorial function: the value of factorial(1) is 1. Recursion Call/Recursive Step: the method calls a “fresh” copy of itself (this is used to work on a smaller version of the problem) and often includes a return statement 6

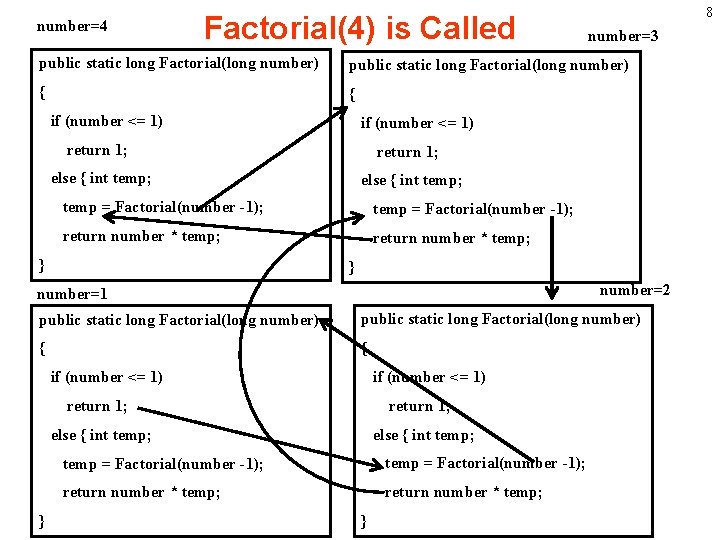
7 Factorial Method public static long Factorial(long number) { // base case if (number <= 1) return 1; // recursion step else return number * Factorial(number -1); }

number=4 Factorial(4) is Called 8 number=3 public static long Factorial(long number) { { if (number <= 1) return 1; else { int temp; temp = Factorial(number -1); return number * temp; } } number=2 number=1 public static long Factorial(long number) { { if (number <= 1) return 1; else { int temp; temp = Factorial(number -1); return number * temp; } }

9 Why a recursive method works? • A recursive method has its own fresh copy when it is called. – All variables such as parameters and local variables have their own copies. In Factorial method, variables such as number and temp have their own copies. The copies of number and temp when number=4 is different from the copies of number and temp when number=3

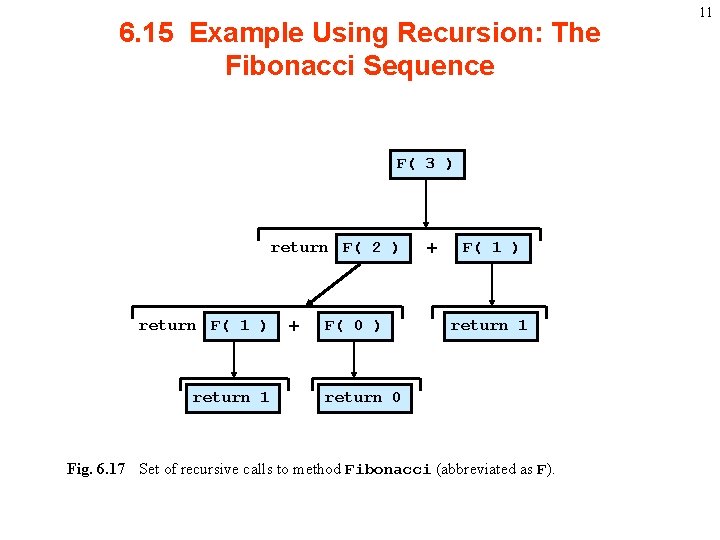
Example Using Recursion: The Fibonacci Sequence • What is importance of Fibonacci Sequence – http: //en. wikipedia. org/wiki/Fibonacci_number – http: //people. bath. ac. uk/lec 20/uses. html • Fibonacci Sequence – – F(0) = 0 F(1) = 1 F(n) = F(n - 1) + F(n - 2) Recursion is used to evaluate F(n) • Complexity theory – How hard computers need to work to perform algorithms 10

6. 15 Example Using Recursion: The Fibonacci Sequence F( 3 ) return F( 2 ) return F( 1 ) return 1 + F( 0 ) + F( 1 ) return 1 return 0 Fig. 6. 17 Set of recursive calls to method Fibonacci (abbreviated as F). 11

How to Ensure DCG When Using Recursion • The key to use the recursion is to find whether the subtask is the same as the original task but in a small size. • To do so, you need to write the clear and unambiguous method specification. (What does the method do, what does each parameter denote, and what does the method return) 12

13 Exercise • Given an integer array A=[2, 1, 44, 3, 2, 54, 1, 66], calculate the sum of the first n elements Calulate. Sum. Of. Array(int[] A, int n )

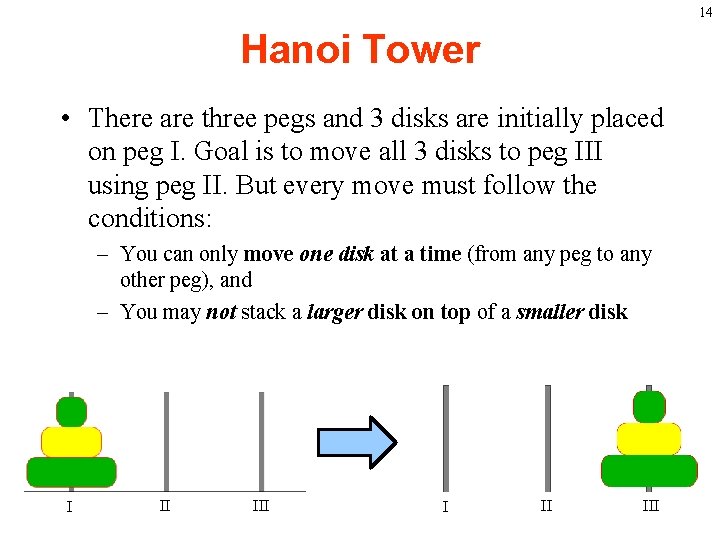
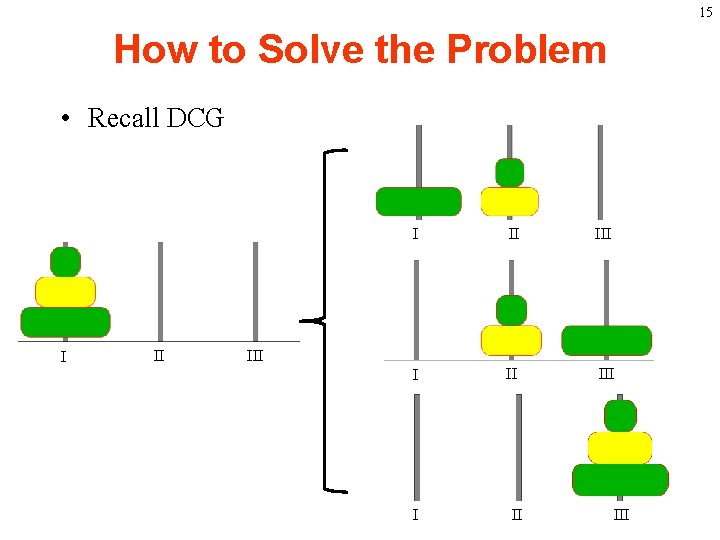
14 Hanoi Tower • There are three pegs and 3 disks are initially placed on peg I. Goal is to move all 3 disks to peg III using peg II. But every move must follow the conditions: – You can only move one disk at a time (from any peg to any other peg), and – You may not stack a larger disk on top of a smaller disk I II III

15 How to Solve the Problem • Recall DCG I II III

16 How to Solve the Problem • Specify the following method n: is the number of disks to be moved from. Peg, and to. Peg denote the pegs where disks are moved from and to respectively. temp. Peg is the temporary peg used during the movement. move. Discs(int n, int from. Peg, int temp. Peg, int to. Peg) { if (n >0) { move. Discs(n-1, from. Peg, to. Peg, temp. Peg); system. out. print(“disc’’+ n + “is moved from”+from. Peg + “ to ” + to. Peg); move. Discs(n-1, temp. Peg, from. Peg, to. Peg); } }

17 What is Wrong? n: is the number of disks to be moved ? ? ? from. Peg, and to. Peg denote the pegs where disks move from and to respectively. temp. Peg is the temporary peg used during the movement. move. Discs(int n, int from. Peg, int temp. Peg, int to. Peg) { if (n >0) { move. Discs(n/2, from. Peg, to. Peg, temp. Peg); move. Discs(n-n/2, from. Peg, temp. Peg, to. Peg); Illegal Move!!! move. Discs(n/2, temp. Peg, from. Peg, to. Peg); } } In OO Programming, You must write a clear specification for what you have programmed!!!

18 What is Correct Spec? All disks has been number from 1, 2, . . , n with 1 denoting the smallest one and n the largest one n: is the largest disk number to be moved, i. e. disk 1, disk 2, …, disk n are to be moved from. Peg, and to. Peg denote the pegs where disks move from and to respectively. temp. Peg is the temporary peg used during the movement. move. Discs(int n, int from. Peg, int temp. Peg, int to. Peg) { if (n >0) { move. Discs(n/2, from. Peg, to. Peg, temp. Peg); move. Discs(n-n/2, from. Peg, temp. Peg, to. Peg); This is not a correct solution!!! move. Discs(n/2, temp. Peg, from. Peg, to. Peg); } } Based on the above specification, can you find another Solution to the Hanoi Tower Problem via DCG?