CS 110 Introduction to Computer Science Lets Make









- Slides: 11

CS 110: Introduction to Computer Science Let’s Make A Deal Debating Value, Decisions, and Probabilities Many people debate basic questions of chance in games such as lotteries. The Monty Hall problem is a fun brain teaser that Marilyn vos Savant addressed in Parade Magazine. Many people didn't believe her answer (which was correct), will you? Core Quantitative Issue Computation of Winning Odds and Probabilities Supporting Computational Issues Random Numbers Combinations and choice Lotteries Experimental Science Prepared by Fred Annexstein University of Cincinnati CC Some rights reserved. 2007 1

The Monty Hall Puzzle • • Let’s suppose you're on a popular 70 s game show, something like "Let's Make a Deal”. In that show the host, Monty Hall, would offer to let you choose from doors 1, 2 or 3, one of which contained a nice prize, like a hot car. But the others doors had lame prizes like a goat. After you have chosen a door, Monty Hall would offer you money or allow you to change your choice. It was all very silly… Now for a formal definition of the actual puzzle: You're offered a choice of doors 1, 2 and 3. You know that behind one of them is a hot car, and behind the other two are goats. You must choose one door. Monty Hall opens one of the other doors to reveal a goat. (Note that, because there are two goats, he can always do this. ) He offers you a chance to switch to the other door. Should you? Is there any value in switching or in sticking? 2

Decisions, Decisions An Argument for Sticking • Since Monty Hall can always open a door to reveal a goat, he has given you no information. So, there are now two doors and the chance of winning the car is now 1/2 instead of 1/3, but the chances are equally likely. You might as well stick, since there's no gain in switching. An Argument for Switching • Your original probability of winning was 1/3, and if you stick, that probability doesn't change. Therefore, the probability of winning if you switch must be 2/3. Which Argument is Right? • Think about this for a while. Could you design an experiment to test both strategies? 3

Produce the following sample spreadsheet Run experiments in which you win the car, or win the goat. Use this to estimate the probability of winning the car with each method. Run this experiment 100 times. And compute the winning percentages. Make sure that the sum is 100%. 4

Probability as a Measure of Knowledge Suppose that, at the very end, someone walks into the room and is offered the same choice. For them, there are now two doors, so the chances of winning are 1/2. For you, the chances of winning are 2/3, since you know something they don't: you know your original choice. So probabilities are not the same for everyone; Strange, isn't it? To determine probabilities, we can't just look at the number of choices and divide. Sometimes, it can be more subtle. Knowledge is power! 5

Lotteries Question: Is it better to spend $50 on one lottery or $1 on 50 lotteries? 6

Lotteries: A game of combinations and chance • If there are 40 balls and 6 are chosen, there are 40 possible numbers that can come up first, leaving 39 that can come up second, then 38, 37, 36, and finally 35 on the final number. To find out how many numbers that is you multiply 40 × 39 × 38 × 37 × 36 × 35 = 2, 763, 633, 600 making the odds of picking numbers in that order less than 2 and a half billion to one. • Pretty slim odds, but luckily the order of the balls does not matter, so we can divide this number by how many ways these numbers can be arranged. There are six possibilities for the first ball, five for the second, 4 for the third, 3, 2, and one left over. That is 6 × 5 × 4 × 3 × 2 × 1 = 720 So, the odds are 2, 763, 633, 600 ÷ 720 = 3, 838, 380 to one. Mathematically, suppose a lottery game is played with n the highest numbered ball and r is the number of balls chosen. • The odds of this style lottery can be found with a simple formula: n! / (n - r)! r! where n! = n*n-1*n-2*…*1 is the factorial function • In Excel this formula is written =FACT(n) / (FACT(n–r) * FACT(r)) : try it! • In mathematics this formula is called a combination or binomial coefficient which in Excel is =COMB(n, r) : try it with n=40 and r=6 and make sure they produce same 7 result as using the factorial formula above.

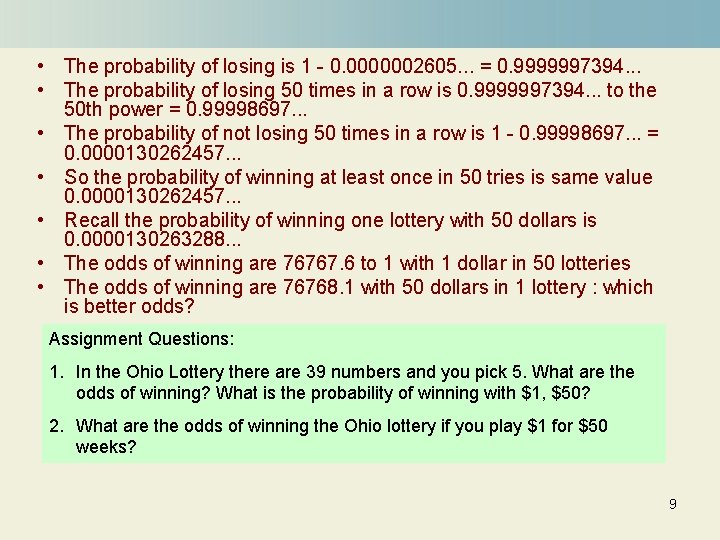
Computing the Odds and the Probabilities So if I put $50 on one lottery, the odds of winning are 3, 838, 380 ÷ 50 = 76767. 6 to one. That is the easy part. • The harder part is calculating the odds of winning if I put $1 on 50 lotteries. To do this we have to convert to probabilities. A probability is a number between 1 and 0. Probability of 1 means a “sure thing”, 0 means “not a chance”. • The probability of winning the lottery with one dollar is 1 ÷ 3, 838, 380 = 0. 0000002605. . . in other words, very small chance. • The probability of winning the lottery with 50 dollars is 1 ÷ 76767. 6 = 0. 0000130263288. . . a bit better chance. • Just for your information, the probability of winning twice in a row is the probability squared which is 0. 00000006. This is not very useful information except that we can use this formula in reverse: the probability of not winning twice in a row is 1 minus that number. • A cold, hard fact: the probability of winning is one minus the probability of losing. The probability of winning at least once in 50 tries is the same as the probability of not losing 50 times in a row. • Let’s do the math…. 8

• The probability of losing is 1 - 0. 0000002605. . . = 0. 9999997394. . . • The probability of losing 50 times in a row is 0. 9999997394. . . to the 50 th power = 0. 99998697. . . • The probability of not losing 50 times in a row is 1 - 0. 99998697. . . = 0. 0000130262457. . . • So the probability of winning at least once in 50 tries is same value 0. 0000130262457. . . • Recall the probability of winning one lottery with 50 dollars is 0. 0000130263288. . . • The odds of winning are 76767. 6 to 1 with 1 dollar in 50 lotteries • The odds of winning are 76768. 1 with 50 dollars in 1 lottery : which is better odds? Assignment Questions: 1. In the Ohio Lottery there are 39 numbers and you pick 5. What are the odds of winning? What is the probability of winning with $1, $50? 2. What are the odds of winning the Ohio lottery if you play $1 for $50 weeks? 9

Expected Return • Another way to look at lotteries is with expected returns. This insight gives another advantage, if you wait for the jackpot to exceed the odds of winning. EXPECTED RETURN = (POTENTIAL WINNING * PROBABILITY OF WINNING)(POTENTIAL COST * PROBABILITY OF LOSING) • Given the lottery above, if the jackpot starts at $1 million, the potential winning is 1 million, the probability of winning is 0. 0000002605. . . , the potential cost is $1. • The expected return is 0. 2605 - 1 = -0. 7395, or a loss of 74 cents. • A positive expected return can be found by waiting for the jackpot to exceed $3, 838, 380. A four million dollar jackpot for example would have a positive expected gain of 4 cents. 10

Power Ball • On July 29, 1998 the 20 state Power Ball lottery gave away a record $250, 000 or a quarter of a billion dollars. The odds of winning at the time were around 80 million to 1 per $1 ticket. • The odds are calculated as follows: There were 49 white balls in which 5 are chosen, the order does not matter. Then one of 42 red balls is chosen. All need to match to win. Thus we have the formula for the number of combinations: FACT(49)/(FACT(49 -5)*FACT(5)) *42 = 80, 089, 128 Assignment Questions: 1. Compute the expected return on $1 bet on July 29, 1998. 2. Today Powerball is played with 55 white balls and 42 red. How many combinations are there? 3. Compute the expected return of this week’s Powerball Lottery for $1 ticket using the current estimated jackpot; see, www. powerball. com 4. Extra Credit: Design a realistic game of chance that has an infinite expected return? 11