CS 110 Introduction to Computer Science Lab 5

CS 110: Introduction to Computer Science: Lab 5 How Will the Next Congress Look? The Jefferson and Hamilton Debate over Methods of Apportionment How the Founding Fathers designed algorithms for assigning fair representation for the new United States of America Core Quantitative Issue Fairness Computation Supporting Computational Issues Fairness Division Political Arithmetic Algorithmic Method Paradox Undecidability Prepared by Fred Annexstein University of Cincinnati CC Some rights reserved. 2007 1

What does the US Constitution say? “Representatives and direct taxes shall be apportioned among the several states which may be included within this union, according to their respective numbers, which shall be determined by adding to the whole number of free persons, including those bound to service for a term of years, and excluding Indians not taxed, three fifths of all other Persons. The actual Enumeration shall be made within three years after the first meeting of the Congress of the United States, and within every subsequent term of ten years, in such manner as they shall by law direct. The number of Representatives shall not exceed one for every thirty thousand, but each state shall have at least one Representative; and until such enumeration shall be made, the state of New Hampshire shall be entitled to choose three, Massachusetts eight, Rhode Island Providence Plantations one, Connecticut five, New York six, New Jersey four, Pennsylvania eight, Delaware one, Maryland six, Virginia ten, North Carolina five, South Carolina five, and Georgia three. ” Article 1, Section 2 of the Constitution of the United States (1787). 2

The Problem of Representation Apportionment The problem of actual assignment of the whole number of seats in the United States Congress among necessarily fractional numbers of relative state populations is known as the problem of Apportionment. • Notes on US Constitution on representation: – – – Not to exceed 1 in 30, 000 of population Women and children are to be counted in population (no voting rights) Slaves counted as 3/5 white person (no voting rights) At least one representative per state Congress given three years to come up with a practical solution. • Two plans were submitted right away: one by Alexander Hamilton and another by Thomas Jefferson. After heated deliberations, Congress applied method of Hamilton. Jefferson’s response: the bill “seems to have avoided establishing [the procedure] into a rule…lest it might not suit on another occasion…[We need to ] reduce the apportionment always to an arithmetical operation, about which no two men can ever possibly differ. ” 3

History of Apportionment I • Jefferson convinced Washington to block Hamilton’s plan by exercising the veto power, the first ever by a President. • After the veto, Congress adopted Jefferson's method, but with a different number of seats. • Senator Daniel Webster’s plan was adopted in 1842, only to be replaced by Hamilton's method in 1852. • 1872 was a very confusing year! First the House size was chosen to be 283 so that Hamilton’s and Webster’s methods would agree. After much political infighting, 9 more seats were added and the final apportionment did not agree with either method. • In 1876 Rutherford B. Hayes became President based on the botched apportionment of 1872. The electoral college vote was 185 for Hayes and 184 for Tilden. 4

A hundred years later, mathematicians M. L. Balinski and H. P. Young showed that Tilden would have won if correct apportionment as required by law had been used. In a celebrated theorem, Balinski and Young (1960 s) showed that any fixed method of apportionment could not always be “fair”. Recall that this result is similar to “Arrow’s Impossibility Theorem” from Lab 4! Electoral College Map 2007 5

Apportionment: Hamilton's Method The following is the apportionment method suggested by Alexander Hamilton was applied by Congress in 1791. Three simple steps are used to find the apportionment. Hamilton’s Method • Step 1. Calculate each state’s standard quota. This standard quota is obtained by using the standard divisor = Total-Population / # Seats State Population Step 1 Quota A 1, 646, 000 32. 92 B 6, 936, 000 138. 72 C 154, 000 3. 08 D 2, 091, 000 41. 82 E 685, 000 13. 70 F 988, 000 19. 76 12, 500, 000 250. 00 Total 6

Apportionment: Hamilton's Method State Hamilton’s Method • Step 2. First give to each state its lower quota obtained by taking the “floor” of the standard quota. Population Step 1 Quota Step 2 Lower Quota A 1, 646, 000 32. 92 32 B 6, 936, 000 138. 72 138 C 154, 000 3. 08 3 D 2, 091, 000 41. 82 41 E 685, 000 13. 70 13 F 988, 000 19. 76 19 12, 500, 000 250. 00 246 Total 7

Apportionment: Hamilton's Method • Step 3. Hamilton gives the surplus seats to the states with the largest fractional parts until there are no more surplus seats. State Population Step 1 Quota Step 2 Lower Quota Fractional parts Rank Surplus Hamilton apportionment A 1, 646, 000 32. 92 32 0. 92 1 33 B 6, 936, 000 138. 72 138 0. 72 4 139 C 154, 000 3. 08 3 0. 08 D 2, 091, 000 41. 82 41 0. 82 E 685, 000 13. 70 13 0. 70 F 988, 000 19. 76 19 0. 76 3 20 12, 500, 000 250. 00 246 4. 00 4 250 Total 3 2 42 13 Hamilton’s Method Satisfies “The Quota Rule”: No state should be apportioned a number of seats smaller than its lower quota or larger than its upper quota. (When a state is apportioned a number smaller than its lower quota, we call it a lower-quota violation; when a state is apportioned a number larger than its upper quota, we call it an upper-quota 8 violation. ) Violations of this rule are considered “unconstitutional”.

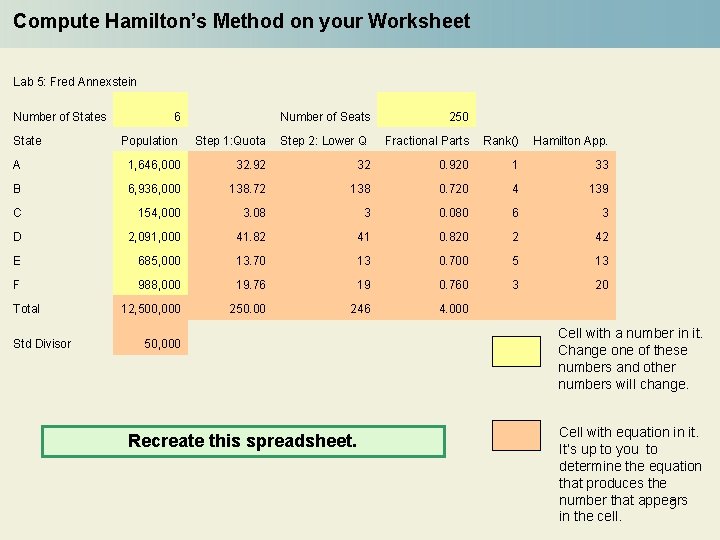
Compute Hamilton’s Method on your Worksheet Lab 5: Fred Annexstein Number of States State 6 Number of Seats 250 Population Step 1: Quota Step 2: Lower Q Fractional Parts Rank() Hamilton App. A 1, 646, 000 32. 92 32 0. 920 1 33 B 6, 936, 000 138. 72 138 0. 720 4 139 C 154, 000 3. 08 3 0. 080 6 3 D 2, 091, 000 41. 82 41 0. 820 2 42 E 685, 000 13. 70 13 0. 700 5 13 F 988, 000 19. 76 19 0. 760 3 20 12, 500, 000 250. 00 246 4. 000 Total Std Divisor 50, 000 Recreate this spreadsheet. Cell with a number in it. Change one of these numbers and other numbers will change. Cell with equation in it. It’s up to you to determine the equation that produces the number that appears 9 in the cell.

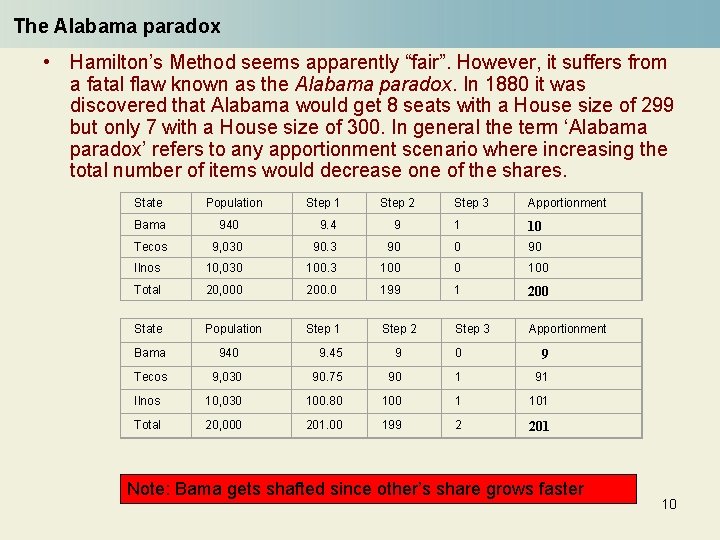
The Alabama paradox • Hamilton’s Method seems apparently “fair”. However, it suffers from a fatal flaw known as the Alabama paradox. In 1880 it was discovered that Alabama would get 8 seats with a House size of 299 but only 7 with a House size of 300. In general the term ‘Alabama paradox’ refers to any apportionment scenario where increasing the total number of items would decrease one of the shares. State Population Step 1 Step 2 Step 3 Apportionment Bama 940 9. 4 9 1 10 Tecos 9, 030 90. 3 90 0 90 Ilnos 10, 030 100. 3 100 0 100 Total 20, 000 200. 0 199 1 200 State Population Step 1 Step 2 Step 3 Apportionment Bama 940 9. 45 9 0 9 Tecos 9, 030 90. 75 90 1 91 Ilnos 10, 030 100. 80 100 1 101 Total 20, 000 201. 00 199 2 201 Note: Bama gets shafted since other’s share grows faster 10

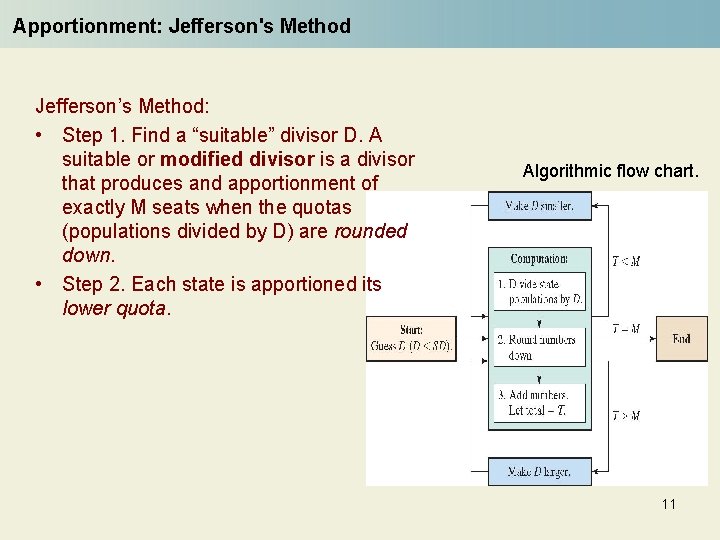
Apportionment: Jefferson's Method Jefferson’s Method: • Step 1. Find a “suitable” divisor D. A suitable or modified divisor is a divisor that produces and apportionment of exactly M seats when the quotas (populations divided by D) are rounded down. • Step 2. Each state is apportioned its lower quota. Algorithmic flow chart. 11

Apportionment: Jefferson's Method • Compute Jefferson’s method in your worksheet. Number of States State Number of Seats 6 250 Population Step 1: Quota Step 2: Lower Q Modified Quota Jefferson App. A 1, 646, 000 32. 92 32 33. 253 33 B 6, 936, 000 138. 72 138 140. 121 140 C 154, 000 3. 08 3 3. 111 3 D 2, 091, 000 41. 82 41 42. 242 42 E 685, 000 13. 70 13 13. 838 13 F 988, 000 19. 76 19 19. 960 19 12, 500, 000 250. 00 246 252. 525 250 Total Std Divisor 50, 000 Modified Divisor 49, 500 Are there upper-quota violations? Which state(s)? Note that they tend to consistently favor the larger states. What is the smallest Modified Divisor that works for Jefferson? 12

Apportionment: Adams’ Method: Like Jefferson’s Method, but for Adams the “suitable” divisor is used to round up. • Step 1. Find a “suitable” divisor D that produces an apportionment of exactly M seats when the quotas (populations divided by D) are rounded up. • Step 2. Every state gets its upper-quota. • Produce on your worksheet a computation of Adams’ Method. Are there upper-quota violations? Which state(s)? Note that they tend to consistently favor the larger states. What is the largest Modified Divisor that works for Adams? Give an argument (informally) that shows that Jefferson favors larger states and Adams favors smaller states. 13

Apportionment: Webster's Method Webster’s Method • Like Jefferson’s and Adams’, but now the “suitable” divisor is used to round in the conventional way. • Step 1. Find a “suitable” divisor D that produces an apportionment of exactly M seats when the quotas (populations divided by D) are rounded conventionally. • Step 2. Every state gets its rounded quota. • Produce on your worksheet a computation of Webster’s Method. Are there any lower or upper-quota violations? In practice they are surprisingly rare. Many consider Webster’s the best possible method. Webster’s method was adopted by the Congress in 1842, and then replaced by Alexander Hamilton's in 1852. It was again adopted in 1901 and reconfirmed in 1911. Finally, it was replaced by Huntington-Hill's method in 1941 and was used in the latest reapportionment in 2000. Turn in your worksheet on the 4 methods discussed in this lab. You may continue on to your Midterm Homework Project. 14

Apportionment: Huntington Method In 1921 Edward V. Huntington, a Harvard mathematician proposed a solution known as the “method of equal proportions. ” Huntington’s Test of Fairness: Any fair apportionment should have the property that it is not possible to transfer a representative (from one state to another) and improve their relative difference in (average) district sizes. TABLE OF MULTIPLIERS Huntington shows such apportionments always exist and there is a solution method “of little interest except to the computers in the Bureau of the Census. ” Transactions of AMS, 1928 1 0. 707106781 2 0. 577350269 3 0. 288675135 . …… ……. . N 1/SQRT(N*N+1) 15