CS 105 Tour of the Black Holes of

CS 105 “Tour of the Black Holes of Computing” Machine-Level Programming IV: Structured Data Topics n Arrays n Structs Unions n

Basic Data Types Integral n Stored & operated on in general registers n Signed vs. unsigned depends on instructions used Intel byte word double word quad word GAS b w l q Bytes 1 2 4 8 C [unsigned] char short int long Floating Point n Stored & operated on in floating-point registers Intel Single Double – 2– GAS s l Bytes 4 8 C float double 105

Array Allocation Basic Principle T A[L]; n n Array of data type T and length L Contiguously allocated region of L * sizeof(T) bytes in memory char string[12]; x x + 12 int val[5]; x x+4 x+8 x + 12 x + 16 x + 20 double a[3]; x x+8 x + 16 x + 24 char *p[3]; – 3– x + 16 x + 24 105

Array Access Basic Principle T A[L]; Array of data type T and length L n Identifier A can be used as a pointer to array element 0 n int val[5]; 1 x Reference val[4] val+1 &val[2] val[5] *(val+1) val + i – 4– Type Value int[5] int * int int * 3 x x+4 x+8 ? ? 5 x+4 i 5 x+4 2 x+8 1 3 x + 12 x + 16 x + 20 (acts like int *) 105

Array Example int cmu[5] = {1, 5, 2, 1, 3}; int mit[5] = {0, 2, 1, 3, 9}; int hmc[5] = {9, 1, 7, 1, 1}; int cmu[5]; 1 16 int mit[5]; 20 0 36 int hmc[5]; Note: n 5 24 2 40 9 56 2 44 32 3 48 7 64 3 28 1 1 60 1 36 9 52 1 68 56 1 72 76 Example arrays were allocated in successive 20 -byte blocks l Not guaranteed to happen in general n – 5– Here, [5] could be omitted because initializer implies size 105

Array Accessing Example 1 int cmu[5]; 16 5 20 2 24 1 28 int get_digit(int z[], int digit) { return z[digit]; } 3 32 n n x 86 -64 # %rdi = z # %rsi = digit movl (%rdi, %rsi, 4), %eax – 6– n 36 As argument, size of z doesn’t need to be specified Register %rdi contains starting address of array Register %rsi contains array index Desired digit at %rdi + 4*%rsi Use memory reference (%rdi, %rsi, 4) # z[digit] 105

Referencing Examples int cmu[5]; 1 16 int mit[5]; 5 20 0 36 int hmc[5]; 24 2 40 9 56 2 3 28 1 44 1 60 1 32 3 48 7 64 9 52 1 68 36 56 1 72 76 Code Does Not Do Any Bounds Checking! Reference mit[3] mit[5] mit[-1] cmu[15] n – 7– Address 36 36 36 16 + + 4* 3 4* 5 4*-1 4*15 Value = = 48 56 32 76 Guaranteed? 3 9 3 ? ? Yes No No No Out-of-range behavior implementation-dependent l No guaranteed relative allocation of different arrays 105

Referencing Examples int cmu[5]; 1 16 int mit[5]; 5 20 0 36 int hmc[5]; 24 2 40 9 56 2 3 28 1 44 1 60 1 32 3 48 7 64 9 52 1 68 36 56 1 72 76 Code Does Not Do Any Bounds Checking! Reference mit[3] mit[5] mit[-1] cmu[15] n – 8– Address 36 36 36 16 + + 4* 3 4* 5 4*-1 4*15 Value = = 48 56 32 76 Guaranteed? 3 9 3 ? ? Out-of-range behavior implementation-dependent l No guaranteed relative allocation of different arrays 105

Array Loop Example void zincr(int z[5]) { size_t i; for (i = 0; i < 5; i++) z[i]++; } # %rdi = z movl $0, jmp. L 3. L 4: addl $1, addq $1, . L 3: cmpq $4, jbe. L 4 rep; ret – 9– %eax # i = 0 # goto middle # loop: (%rdi, %rax, 4) # z[i]++ %rax # i++ # middle %rax # i: 4 # if <=, goto loop 105

Multidimensional (Nested) Arrays Declaration T A[R][C]; n 2 D array of data type T R rows, C columns n Type T element requires K bytes n A[0][0] • • • Array Size n A[0][C-1] • • • A[R-1][0] R * C * K bytes • • • A[R-1][C-1] Arrangement n Row-Major Ordering int A[R][C]; A [0] – 10 – A A • • • [0] [1] [C-1] [0] A • • • [1] [C-1] 4*R*C Bytes • • • A A [R-1] • • • [R-1] [0] [C-1] 105

Nested Array Example #define PCOUNT 4 int pgh[PCOUNT][5] = {{1, 5, 2, 0, 6}, {1, 5, 2, 1, 3 }, {1, 5, 2, 1, 7 }, {1, 5, 2, 2, 1 }}; int pgh[4][5]; 1 5 2 0 6 1 5 2 1 3 1 5 2 1 7 1 5 2 2 1 76 96 116 136 156 Variable pgh: array of 4 elements, allocated contiguously n Each element is an array of 5 int’s, allocated contiguously “Row-Major” ordering of all elements in memory – 11 – 105

Nested Array Row Access Row Vectors n A[i] is array of C elements n Each element of type T requires K bytes Starting address A + i * (C * K) n int A[R][C]; A[0] A – 12 – • • • A[i] A [0] [C-1] • • • A [i] [0] • • • A+(i*C*4) A[R-1] A [i] [C-1] A • • • [R-1] [0] • • • A [R-1] [C-1] A+((R-1)*C*4) 105

Nested Array Element Access Array Elements n n A[i][j] is element of type T, which requires K bytes Address A + i * (C * K) + j * K = A + (i * C + j) * K int A[R][C]; A[0] A • • • A[i] A [0] • • • [C-1] • • • A [i] [j] A[R-1] • • • A+i*C*4 A • • • [R-1] [0] • • • A [R-1] [C-1] A+(R-1)*C*4 A+(i*C+j)*4 – 13 – 105

Strange Referencing Examples int pgh[4][5]; 1 5 2 0 6 1 5 2 1 3 1 5 2 1 7 1 5 2 2 1 76 Reference Address pgh[3][3] pgh[2][5] pgh[2][-1] pgh[4][-1] pgh[0][19] pgh[0][-1] 76+20*3+4*3 = 148 76+20*2+4*5 = 136 76+20*2+4*-1 = 112 76+20*4+4*-1 = 152 76+20*0+4*19 = 152 76+20*0+4*-1 = 72 96 116 Value 2 1 3 1 1 ? ? 136 156 Guaranteed? Yes Yes Yes No Code does not do any bounds checking n Ordering of elements within array guaranteed n – 14 – 105

Strange Referencing Examples int pgh[4][5]; 1 5 2 0 6 1 5 2 1 3 1 5 2 1 7 1 5 2 2 1 76 Reference Address pgh[3][3] pgh[2][5] pgh[2][-1] pgh[4][-1] pgh[0][19] pgh[0][-1] 76+20*3+4*3 = 148 76+20*2+4*5 = 136 76+20*2+4*-1 = 112 76+20*4+4*-1 = 152 76+20*0+4*19 = 152 76+20*0+4*-1 = 72 96 116 Value 136 156 Guaranteed? 2 1 3 1 1 ? ? Code does not do any bounds checking n Ordering of elements within array guaranteed n – 15 – 105

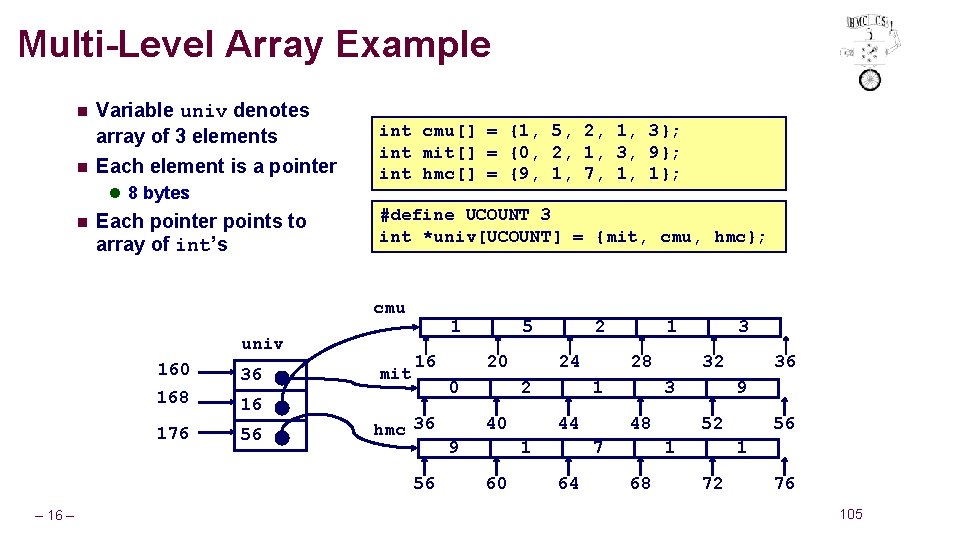
Multi-Level Array Example n n Variable univ denotes array of 3 elements Each element is a pointer l 8 bytes n Each pointer points to array of int’s int cmu[] = {1, 5, 2, 1, 3}; int mit[] = {0, 2, 1, 3, 9}; int hmc[] = {9, 1, 7, 1, 1}; #define UCOUNT 3 int *univ[UCOUNT] = {mit, cmu, hmc}; cmu univ 160 36 168 16 176 56 mit 1 16 20 0 hmc 36 56 – 16 – 5 2 24 2 40 9 28 1 44 1 60 1 32 3 48 7 64 3 9 52 1 68 36 56 1 72 76 105

Element Access in Multi-Level Array int get_univ_digit(size_t index, size_t digit) { return univ[index][digit]; } salq addq movl ret $2, %rsi # 4*digit univ(, %rdi, 8), %rsi # p = univ[index] + 4*digit (%rsi), %eax # return *p Computation n Element access Mem[univ+8*index]+4*digit] n Must do two memory reads l First get pointer to row array l Then access element within array – 17 – 105

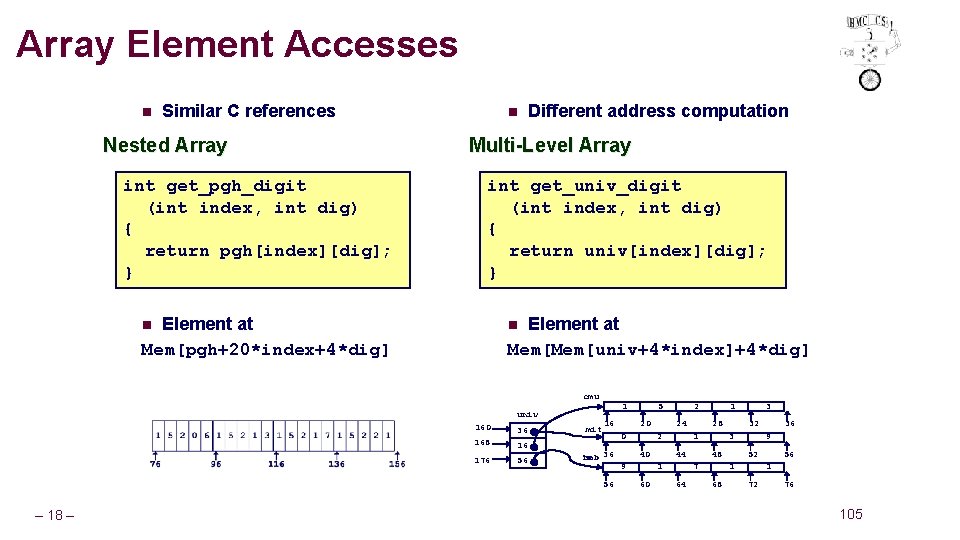
Array Element Accesses n Similar C references Nested Array int get_pgh_digit (int index, int dig) { return pgh[index][dig]; } n Different address computation Multi-Level Array int get_univ_digit (int index, int dig) { return univ[index][dig]; } Element at Mem[pgh+20*index+4*dig] Element at Mem[univ+4*index]+4*dig] n n cmu univ 160 36 168 16 176 56 mit 1 16 20 0 ucb 36 hmc 56 – 18 – 5 2 24 2 40 9 28 1 44 1 4 60 1 32 3 48 7 64 3 52 1 2 68 36 9 56 1 0 72 76 105

Strange Referencing Examples cmu univ 160 36 168 16 176 56 mit 1 16 56 univ[2][3] univ[1][5] univ[2][-1] univ[3][-1] univ[1][12] n n – 19 – 56+4*3 16+4*5 56+4*-1 ? ? 16+4*12 = 68 = 36 = 52 = 64 20 0 hmc 36 Reference Address 5 2 24 2 40 9 28 1 44 1 60 1 32 3 48 7 64 3 36 9 52 1 68 56 1 72 76 Value Guaranteed? 1 0 9 ? ? 7 Code does not do any bounds checking Ordering of elements in different arrays not guaranteed Yes No No 105

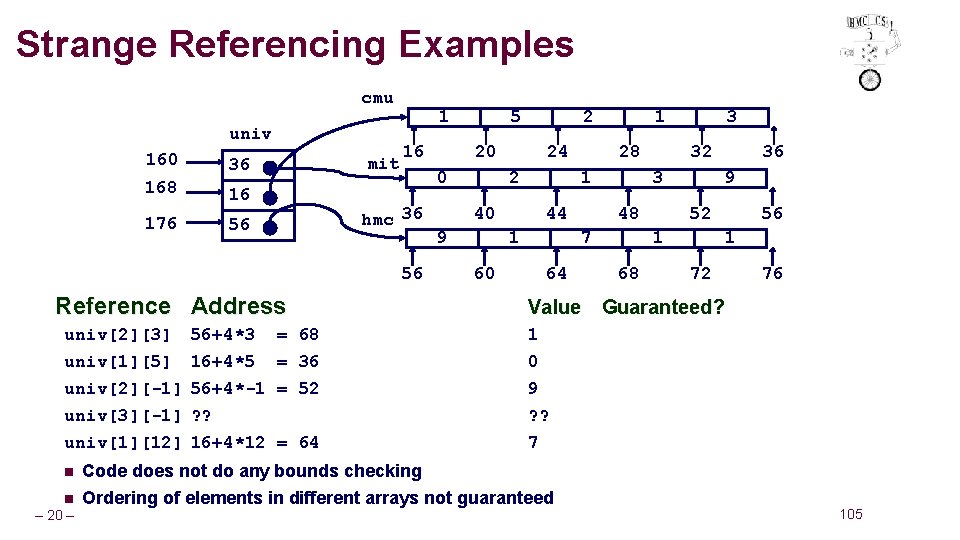
Strange Referencing Examples cmu univ 160 36 168 16 176 56 mit 1 16 56 univ[2][3] univ[1][5] univ[2][-1] univ[3][-1] univ[1][12] n n – 20 – 56+4*3 16+4*5 56+4*-1 ? ? 16+4*12 = 68 = 36 = 52 = 64 20 0 hmc 36 Reference Address 5 2 24 2 40 9 28 1 44 1 60 1 32 3 48 7 64 3 9 52 1 68 36 56 1 72 76 Value Guaranteed? 1 0 9 ? ? 7 Code does not do any bounds checking Ordering of elements in different arrays not guaranteed 105

N X N Matrix Code Fixed dimensions n Know value of N at compile time Variable dimensions, explicit indexing n Traditional way to implement dynamic arrays Variable dimensions, implicit indexing n – 21 – Now supported by gcc #define N 16 typedef int fix_matrix[N][N]; /* Get element a[i][j] */ int fix_ele(fix_matrix a, size_t i, size_t j) { return a[i][j]; } #define IDX(n, i, j) ((i)*(n)+(j)) /* Get element a[i][j] */ int vec_ele(size_t n, int *a, size_t i, size_t j) { return a[IDX(n, i, j)]; } /* Get element a[i][j] */ int var_ele(size_t n, int a[n][n], size_t i, size_t j) { return a[i][j]; } 105

16 X 16 Matrix Access ¢ Array Elements § Address A + i * (C * K) + j * K § C = 16, K = 4 /* Get element a[i][j] */ int fix_ele(fix_matrix a, size_t i, size_t j) { return a[i][j]; } # a in %rdi, i in %rsi, j in salq $6, %rsi addq %rsi, %rdi movl (%rdi, %rdx, 4), %eax ret – 22 – %rdx # 64*i # a + 64*i # M[a + 64*i + 4*j] 105

n X n Matrix Access ¢ Array Elements § Address A + i * (C * K) + j * K § C = n, K = 4 § Must perform integer multiplication /* Get element a[i][j] */ int var_ele(size_t n, int a[n][n], size_t i, size_t j) { return a[i][j]; } # n in %rdi, a in %rsi, i in imulq %rdx, %rdi leaq (%rsi, %rdi, 4), %rax movl (%rax, %rcx, 4), %eax ret – 23 – %rdx, j in %rcx # n*i # a + 4*n*i + 4*j 105

Structure Representation r struct rec { int a[4]; size_t i; struct rec *next; }; a 0 i 16 next 24 32 Structure represented as block of memory n Big enough to hold all of the fields Fields ordered according to declaration n Even if another ordering could yield a more compact representation Compiler determines overall size + positions of fields n – 24 – Machine-level program has no understanding of the structures in the source code 105

Generating Pointer to Structure Member r struct rec { int a[4]; size_t i; struct rec *next; }; Generating Pointer to Array Element n n Offset of each structure member determined at compile time Compute as r + 4*idx r+4*idx a 0 i 16 next 24 32 int *get_ap (struct rec *r, size_t idx) { return &r->a[idx]; } # r in %rdi, idx in %rsi leaq (%rdi, %rsi, 4), %rax ret – 25 – 105

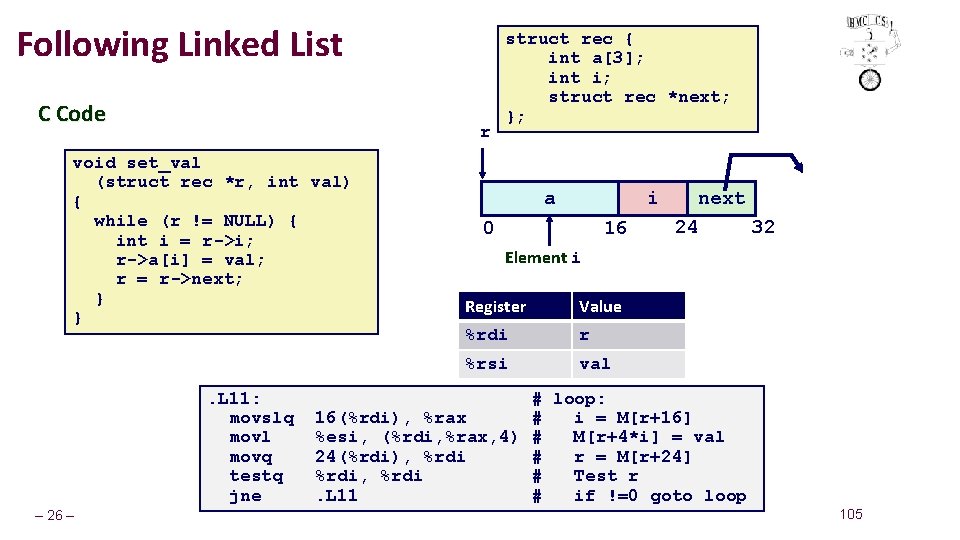
Following Linked List C Code r void set_val (struct rec *r, int val) { while (r != NULL) { int i = r->i; r->a[i] = val; r = r->next; } } . L 11: movslq movl movq testq jne – 26 – struct rec { int a[3]; int i; struct rec *next; }; a i 16 0 next 24 32 Element i Register Value %rdi r %rsi val # loop: 16(%rdi), %rax # i = M[r+16] %esi, (%rdi, %rax, 4) # M[r+4*i] = val 24(%rdi), %rdi # r = M[r+24] %rdi, %rdi # Test r. L 11 # if !=0 goto loop 105

Alignment Principles Aligned Data n Primitive data type requires K bytes n Address must be multiple of K Required on some machines; advised on x 86 -64 n Motivation for Aligning Data n Memory accessed by (aligned) chunks of 4 or 8 bytes (system-dependent) l Inefficient to load or store datum that spans quad word boundaries l Virtual memory trickier when datum spans 2 pages Compiler n – 27 – Inserts gaps in structure to ensure correct alignment of fields 105

Structures & Alignment Unaligned Data c i[0] p p+1 i[1] p+5 v p+9 p+17 struct S 1 { char c; int i[2]; double v; } *p; Aligned Data n n c p+0 Primitive data type requires K bytes Address must be multiple of K 3 bytes p+4 i[0] i[1] p+8 Multiple of 4 – 28 – Multiple of 8 4 bytes p+16 v p+24 Multiple of 8 105

Specific Cases of Alignment (x 86 -64) 1 byte: char, … n no restrictions on address 2 bytes: short, … n lowest 1 bit of address must be 02 4 bytes: int, float, … n lowest 2 bits of address must be 002 8 bytes: double, long, char *, … n lowest 3 bits of address must be 0002 16 bytes: long double (GCC on Linux) n – 29 – lowest 4 bits of address must be 00002 105

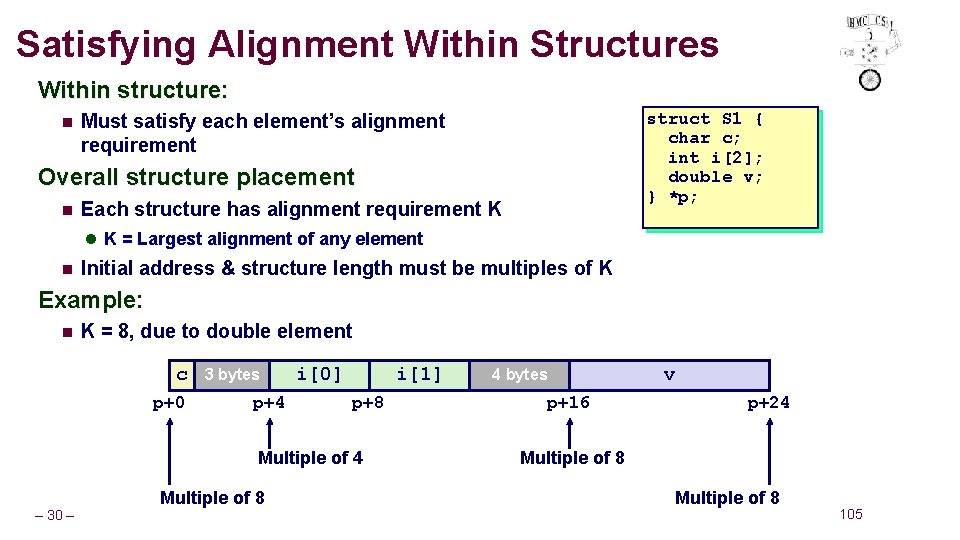
Satisfying Alignment Within Structures Within structure: n struct S 1 { char c; int i[2]; double v; } *p; Must satisfy each element’s alignment requirement Overall structure placement n Each structure has alignment requirement K l K = Largest alignment of any element n Initial address & structure length must be multiples of K Example: n K = 8, due to double element c p+0 3 bytes p+4 i[0] i[1] p+8 Multiple of 4 – 30 – Multiple of 8 4 bytes p+16 v p+24 Multiple of 8 105

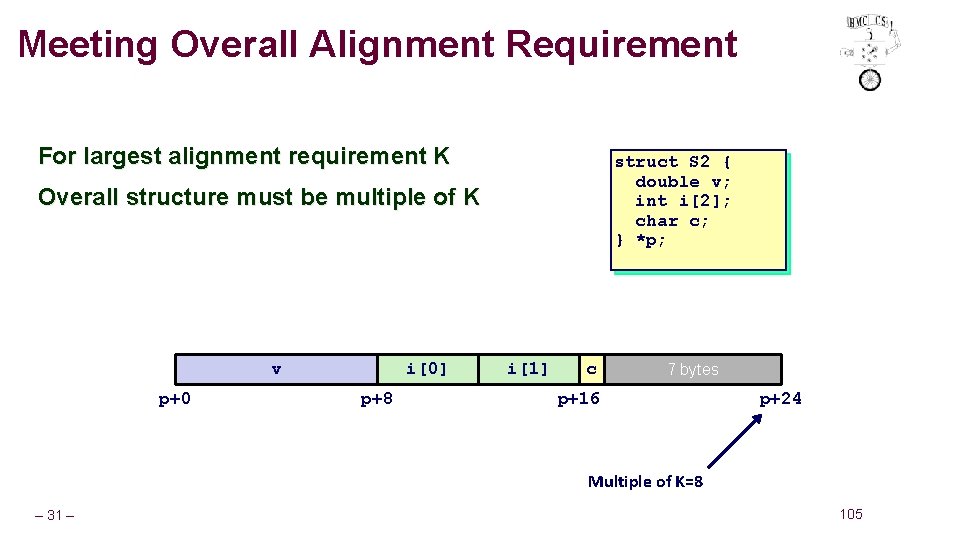
Meeting Overall Alignment Requirement For largest alignment requirement K struct S 2 { double v; int i[2]; char c; } *p; Overall structure must be multiple of K v p+0 i[0] p+8 i[1] c 7 bytes p+16 p+24 Multiple of K=8 – 31 – 105

Arrays of Structures struct S 2 { double v; int i[2]; char c; } a[10]; Overall structure length multiple of K Satisfy alignment requirement for every element a[0] a+0 a[1] a+24 v a+24 – 32 – i[0] a+32 • • • a[2] a+48 i[1] a+72 c a+40 7 bytes a+48 105

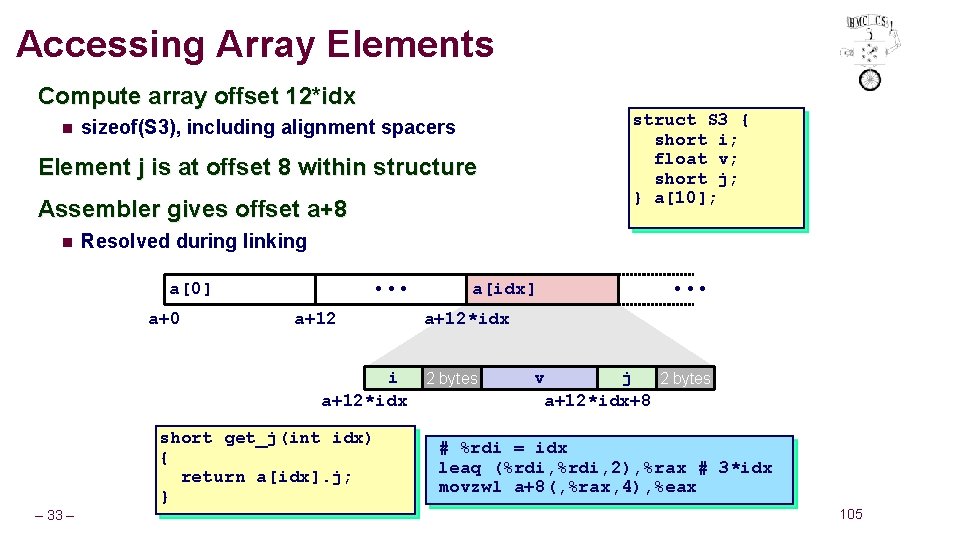
Accessing Array Elements Compute array offset 12*idx n struct S 3 { short i; float v; short j; } a[10]; sizeof(S 3), including alignment spacers Element j is at offset 8 within structure Assembler gives offset a+8 n Resolved during linking • • • a[0] a+0 a+12 i a+12*idx short get_j(int idx) { return a[idx]. j; } – 33 – a[idx] • • • a+12*idx 2 bytes v j 2 bytes a+12*idx+8 # %rdi = idx leaq (%rdi, 2), %rax # 3*idx movzwl a+8(, %rax, 4), %eax 105

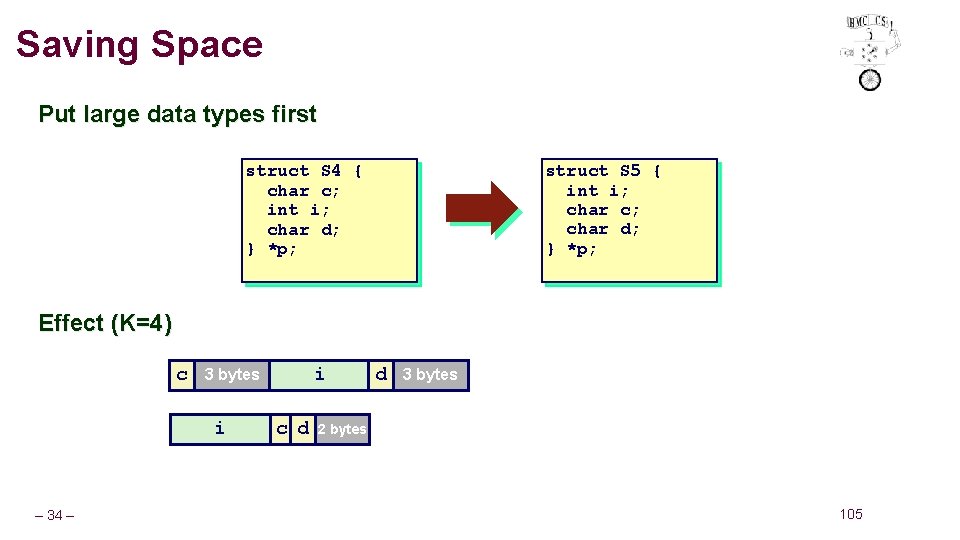
Saving Space Put large data types first struct S 5 { int i; char c; char d; } *p; struct S 4 { char c; int i; char d; } *p; Effect (K=4) c i – 34 – i 3 bytes c d d 3 bytes 2 bytes 105

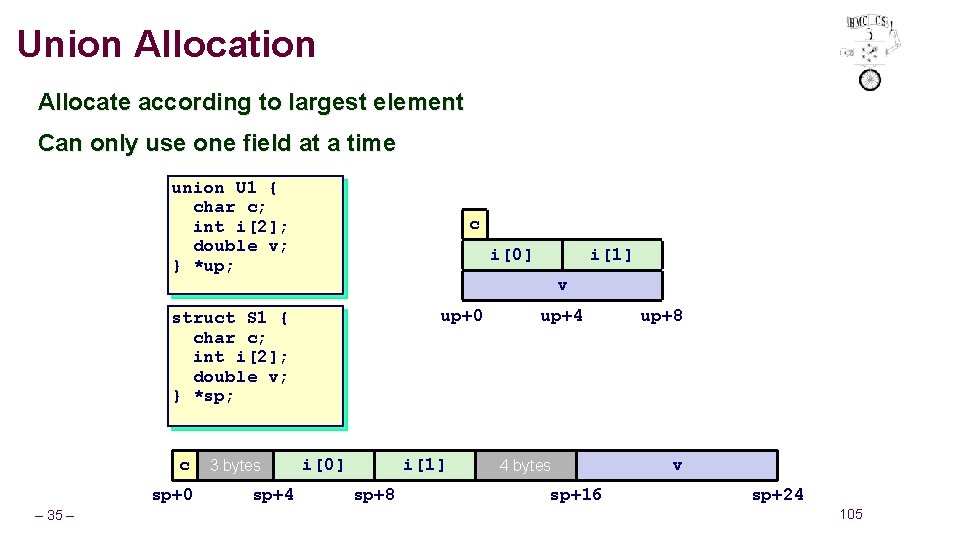
Union Allocate according to largest element Can only use one field at a time union U 1 { char c; int i[2]; double v; } *up; c i[0] v up+0 struct S 1 { char c; int i[2]; double v; } *sp; c sp+0 – 35 – 3 bytes sp+4 i[1] i[0] i[1] sp+8 up+4 4 bytes sp+16 up+8 v sp+24 105

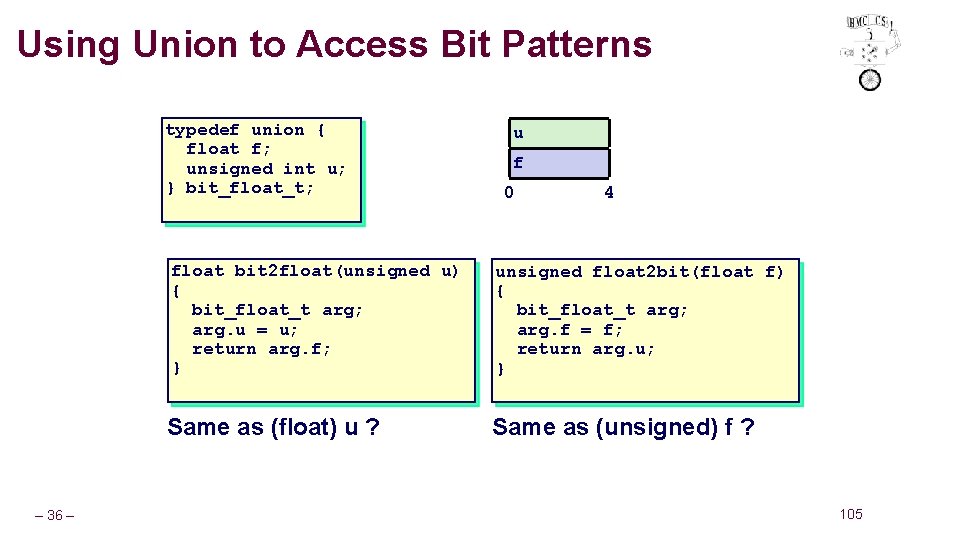
Using Union to Access Bit Patterns typedef union { float f; unsigned int u; } bit_float_t; – 36 – u f 0 4 float bit 2 float(unsigned u) { bit_float_t arg; arg. u = u; return arg. f; } unsigned float 2 bit(float f) { bit_float_t arg; arg. f = f; return arg. u; } Same as (float) u ? Same as (unsigned) f ? 105

Byte Ordering Revisited Idea n n n Short/long/quad words stored in memory as 2/4/8 consecutive bytes Which byte is most (least) significant? Can cause problems when exchanging binary data between machines Big Endian n n Most significant byte has lowest address Sparc Little Endian n n Least significant byte has lowest address Intel x 86, ARM Android and IOS Bi Endian n n – 37 – Can be configured either way ARM 105

Byte Ordering Example union { unsigned } dw; char c[8]; short s[4]; int i[2]; long l[1]; 32 -bit c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] s[0] s[1] s[2] i[0] s[3] i[1] l[0] 64 -bit c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] s[0] s[1] s[2] i[0] – 38 – s[3] i[1] l[0] 105

Byte Ordering Example (Cont). int j; for (j = 0; j < 8; j++) dw. c[j] = 0 xf 0 + j; printf("Characters 0 -7 == [0 x%x, 0 x%x, 0 x%x]n", dw. c[0], dw. c[1], dw. c[2], dw. c[3], dw. c[4], dw. c[5], dw. c[6], dw. c[7]); printf("Shorts 0 -3 == [0 x%x, 0 x%x]n", dw. s[0], dw. s[1], dw. s[2], dw. s[3]); printf("Ints 0 -1 == [0 x%x, 0 x%x]n", dw. i[0], dw. i[1]); printf("Long 0 == [0 x%lx]n", dw. l[0]); – 39 – 105

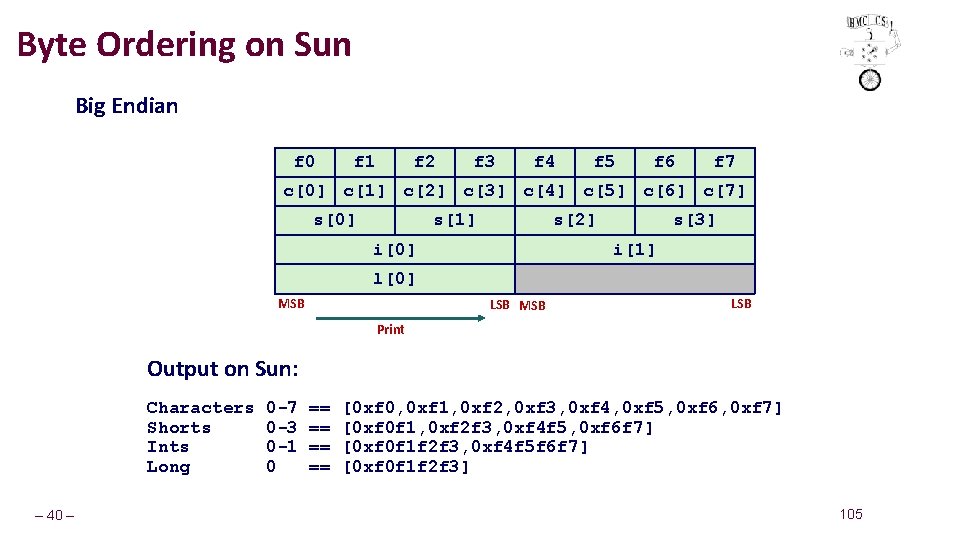
Byte Ordering on Sun Big Endian f 0 f 1 f 2 f 3 f 4 f 5 f 6 f 7 c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] s[0] s[1] s[2] i[0] s[3] i[1] l[0] MSB LSB Print Output on Sun: Characters Shorts Ints Long – 40 – 0 -7 0 -3 0 -1 0 == == [0 xf 0, 0 xf 1, 0 xf 2, 0 xf 3, 0 xf 4, 0 xf 5, 0 xf 6, 0 xf 7] [0 xf 0 f 1, 0 xf 2 f 3, 0 xf 4 f 5, 0 xf 6 f 7] [0 xf 0 f 1 f 2 f 3, 0 xf 4 f 5 f 6 f 7] [0 xf 0 f 1 f 2 f 3] 105

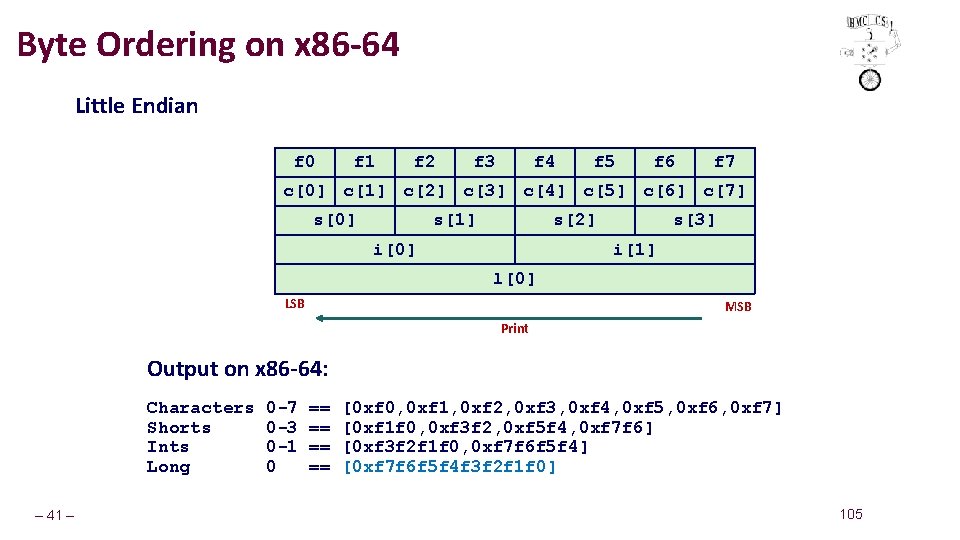
Byte Ordering on x 86 -64 Little Endian f 0 f 1 f 2 f 3 f 4 f 5 f 6 f 7 c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] s[0] s[1] s[2] i[0] s[3] i[1] l[0] LSB MSB Print Output on x 86 -64: Characters Shorts Ints Long – 41 – 0 -7 0 -3 0 -1 0 == == [0 xf 0, 0 xf 1, 0 xf 2, 0 xf 3, 0 xf 4, 0 xf 5, 0 xf 6, 0 xf 7] [0 xf 1 f 0, 0 xf 3 f 2, 0 xf 5 f 4, 0 xf 7 f 6] [0 xf 3 f 2 f 1 f 0, 0 xf 7 f 6 f 5 f 4] [0 xf 7 f 6 f 5 f 4 f 3 f 2 f 1 f 0] 105

Summary of Compound Types in C Arrays n Contiguous allocation of memory n n Aligned to satisfy every element’s alignment requirement Pointer to first element n No bounds checking Structures n n Allocate bytes in order declared Pad in middle and at end to satisfy alignment Unions n n – 42 – Overlay declarations Way to circumvent type system 105