CS 104 Discrete Structures CHAPTER II PROOF TECHNIQUES

CS 104: Discrete Structures CHAPTER II PROOF TECHNIQUES Madawi S. Al. Otaibi Department of Computer Science E-mail: M. Al. Otaibi@ccis. imamu. edu. sa Office # 3143 Chapter 1 (section 1. 6)

Rules of Inference Sec 1. 6 Madawi S. Al. Otaibi 2

Valid Arguments in Propositional Logic 3 q Proofs in mathematics are valid arguments that establish the truth of mathematical statements. Ø Argument: An argument is a sequence of statements that end with a conclusion. Ø Valid: An argument is valid if and only if it is impossible for all premises (preceding statements) to be true and the conclusion to be false. By valid, we mean that the conclusion of the argument must follow from the truth of the premises of the argument. q Consider the argument: (involving propositions) “If you have a current password, then you can log onto the network. ” “You have a current password” Therefore, “You can log onto the network” (Conclusion) Madawi S. Al. Otaibi

Rules of Inference- Valid Arguments in Propositional Logic 4 “If you have a current password, then you can log onto the network. ” p q q The conclusion q : “You can log onto the network” must be True when : The premises p q : “If you have a current password, then you can log onto the network” is True And p: “You have a current password” is True p→q p q where is the symbol that denotes “therefore. ” q Note that whenever we replace p and q by propositions where p → q and p are both true, then q must also be true. q The statement ((p → q) � p) → q is a tautology Madawi S. Al. Otaibi

Rules of Inference- Valid Arguments in Propositional Logic 5 q What happens when we replace p and q in this argument form by propositions where not both p and p → q are true? Ø Example 1. An suppose that: p : “You have access to the network” q: “You can change your grade” and that p is true, but p → q is false. The argument we obtain by substituting these values of p and q into the argument form is: “If you have access to the network, then you can change your grade. ” “You have access to the network. ” ∴ “You can change your grade. ” The argument we obtained is a valid argument, but because one of the premises, namely the first premise, is false, we cannot conclude that the conclusion is true. Madawi S. Al. Otaibi

Rules of Inference- Valid Arguments in Propositional Logic 6 q Definition An argument in propositional logic is a sequence of propositions. All but the final proposition in the argument are called premises and the final proposition is called the conclusion. An argument is valid if the truth of all its premises implies that the conclusion is true. An argument form in propositional logic is a sequence of compound propositions involving propositional variables. An argument form is valid no matter which particular propositions are substituted for the propositional variables in its premises, the conclusion is true if the premises are all true. Madawi S. Al. Otaibi

Rules of Inference for Propositional Logic 7 q We can always use a truth table to show that an argument form is valid by showing that whenever the premises are true, the conclusion must also be true if we have an argument form involves 10 different propositional variables By using truth table 210 = 1024 rows it is tedious approach How we can show that this argument form is valid ? q Instead of showing by truth table, we can establish the validity of some relatively simple argument forms, called rules of inference, which can be used as building blocks to construct more complicated valid argument forms. Madawi S. Al. Otaibi

Rules of Inference for Propositional Logic 8 q The tautology (p ∧ (p → q)) → q is the basis of the rule of inference called modus ponens or law of detachment Ø This tautology leads to the following valid argument form: p p→q q q Example 2: Suppose that the conditional statement “If it snows today, then we will go skiing ” and its hypothesis “ It snows today ” are True. Then, by modus ponens, it follows that the conclusion of the conditional statement “We will go skiing ” are True. Madawi S. Al. Otaibi

Rules of Inference for Propositional Logic 9 q Q 1: Determine whether the argument given here is valid and determine whether its conclusion must be true because of the validity of the argument. p Ø q Solution The premises of the argument are : p → q and p while q is its conclusion This argument is valid because it is constructed by using modus ponens, a valid argument form. Since premises (p → q) � p are false, therefore the conclusion q is also false because Madawi S. Al. Otaibi .

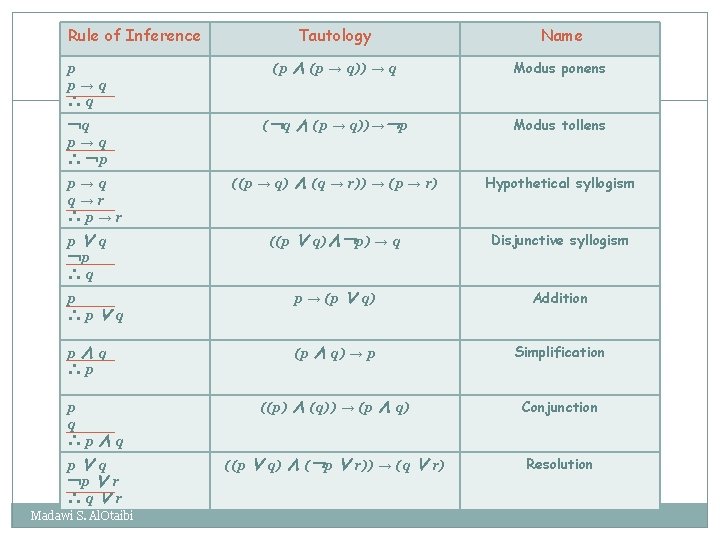
Rule of Inference Tautology Name p p→q ∴q (p ∧ (p → q)) → q Modus ponens ￢q p→q ∴ ￢p (￢q ∧ (p → q))→￢p Modus tollens ((p → q) ∧ (q → r)) → (p → r) Hypothetical syllogism ((p ∨ q)∧￢p) → q Disjunctive syllogism p ∴p∨q p → (p ∨ q) Addition p∧q ∴p (p ∧ q) → p Simplification p q ∴p∧q ((p) ∧ (q)) → (p ∧ q) Conjunction p∨q ￢p ∨ r ∴q∨r ((p ∨ q) ∧ (￢p ∨ r)) → (q ∨ r) Resolution p→q q→r ∴p→r p∨q ￢p ∴q Madawi S. Al. Otaibi 10

Rules of Inference for Propositional Logic 11 q Example 3: State which rule of inference is the basis of the following argument: “It is below freezing now. Therefore, it is either below freezing or raining now ” Ø Solution: Let p be the proposition “It is below freezing now” and q the proposition “It is raining now” Then this argument is of the form: p p∨q This is an argument that uses the addition rule. Madawi S. Al. Otaibi

Rules of Inference for Propositional Logic 12 q Example 4: State which rule of inference is the basis of the following argument: “If it rains today, then we will not have a barbecue today. If we do not have a barbecue today, then we will have a barbecue tomorrow. Therefore, if it rains today, then we will have a barbecue tomorrow. ” Ø Solution: Let p be the proposition “It is raining today” Let q the proposition “We will not have a barbecue today” and r the proposition “We will have a barbecue tomorrow” Then this argument is of the form: p→q q→r p→r Hence, this argument is a hypothetical syllogism. q Q 2: State which rule of inference is the basis of the following argument: “It is below freezing and raining now. Therefore, it is below freezing”. Madawi S. Al. Otaibi

Using Rules of Inference to Build Arguments 13 q When there are many premises, several rules of inference are often needed to show that an argument is valid. q Example : Show that the hypotheses : “it is not sunny this afternoon and it is colder than yesterday , ” “we will go swimming only if it is sunny, ” “if we do not go swimming, then we will take a canoe trip, ” “and “if we take a canoe trip, we will be home by sunset. ” lead to the conclusion “ We will be home by sunset” Madawi S. Al. Otaibi

Using Rules of Inference 14 q SOLUTION Ø Let p: “it is sunny this afternoon” q: “it is colder than yesterday” r: “we will go swimming” s: “we will take a canoe trip” t: “we will be home by sunset” The hypotheses become p ^ q, r p, r s, s t the conclusion is t Madawi S. Al. Otaibi

Using Rules of Inference 15 q We construct an argument to show that our hypotheses lead to desired conclusion as follows Step 1. p ^ q 2. p 3. r p 4. r 5. r s 6. s 7. s t 8. t Reason Hypothesis Simplification using (1) Hypothesis Modus tollens (2, 3) Hypothesis Modus ponens (4, 5) Hypothesis Modus ponens (6, 7) Note: that if we used the truth table, we would end up with 32 rows ( 2^5 = 32) !!! Refer : Example (7 page 67 ) Madawi S. Al. Otaibi

Introduction to Proofs Sec 1. 8 Madawi S. Al. Otaibi 16

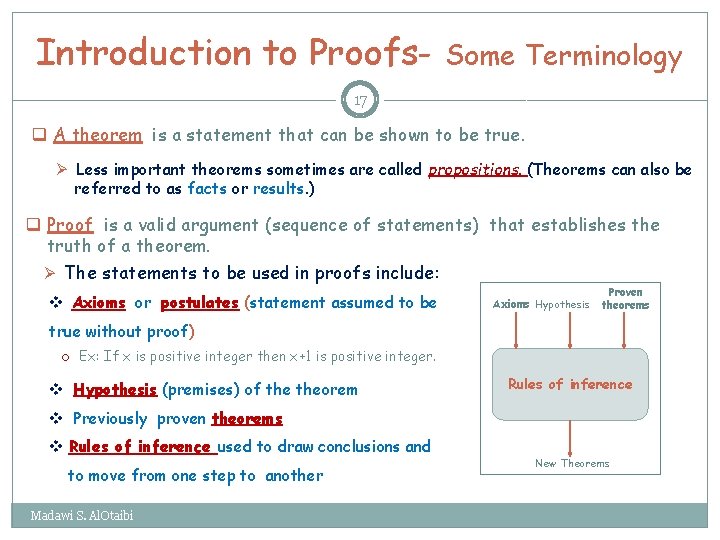
Introduction to Proofs- Some Terminology 17 q A theorem is a statement that can be shown to be true. Ø Less important theorems sometimes are called propositions. (Theorems can also be referred to as facts or results. ) q Proof is a valid argument (sequence of statements) that establishes the truth of a theorem. Ø The statements to be used in proofs include: v Axioms or postulates (statement assumed to be Axioms Hypothesis Proven theorems true without proof) o Ex: If x is positive integer then x+1 is positive integer. v Hypothesis (premises) of theorem Rules of inference v Previously proven theorems v Rules of inference used to draw conclusions and to move from one step to another Madawi S. Al. Otaibi New Theorems

Introduction to Proofs- Some Terminology 18 q Lemma is a less important theorem that is helpful in the proof of other results q A corollary is a theorem that can be established directly from a theorem that has been proved. q A conjuncture is a statement that is being proposed to be a true statement, usually on the basis of some partial evidence q A corollary is a theorem that can be established directly from a theorem that has been proved. Ø When a proof of a conjuncture is found, the conjuncture becomes a theorem Madawi S. Al. Otaibi

Methods of proving theorems 19 q Proving mathematical theorems can be difficult so we need all available ammunition, including a powerful battery of different proof methods Ø These methods provide the overall approach and strategy of proofs q Methods of proving theorems: Ø Direct proofs Ø Proof by Contraposition Ø Proofs by Contradiction Ø Proof by cases Madawi S. Al. Otaibi

Methods of proving theorems – Direct proofs 20 q A direct proof of a conditional statement p q is constructed when the first step is the assumption that p is true; subsequent steps are constructed using rules of inference, with the final step showing that q must also be true. q In a direct proof, we assume that p is true and use axioms, definitions, and previously proven theorems, together with rules of inference, to show that q must also be true. q Definition : The integer n is even if there exists an integer k such that n = 2 k, and n is odd if there exists an integer k such that n = 2 k + 1. Ø Note that every integer is either even or odd, and no integer is both even and odd. Ø Two integers have the same parity when both are even or both are odd; they have opposite parity when one is even and the other is odd. Madawi S. Al. Otaibi

Methods of proving theorems – Direct proofs 21 q Example 5 Give a direct proof of theorem : “If n is an odd integer, then n 2 is odd. ” Ø Proof: We assume that n is odd. (hypothesis) We can square both We sideswant of theto equation n = 2 k + 1 ton 2 obtain show that is a new alsoequation odd. that 2 expresses n. => n = 2 k + 1, where k is some integer. (definition of odd number) => n 2 = (2 k+1)2 = 4 k 2 + 4 k + 1 = 2(2 k 2+2 k)+1 Since r = 2 k 2+2 k is an integer (Axiom) => n 2 = 2 r+1 is odd. q Q 3 Use a direct proof to show that : “If n is an even integer, then n 2 is even. ” Madawi S. Al. Otaibi (By squaring)

Methods of proving theorems – Direct proofs 22 q Methodology of direct proof: Direct proofs lead from the premises of a theorem to the conclusion They begin with the Premises continue with a sequence of deductions End with the conclusion Ø Can we use this methodology to prove theorems of the form ∀x(P(x) → Q(x)) ? Proofs of theorems of this type that are not direct proofs, that is, that do not start with the premises and end with the conclusion. We need other methods of proving this theorem Madawi S. Al. Otaibi

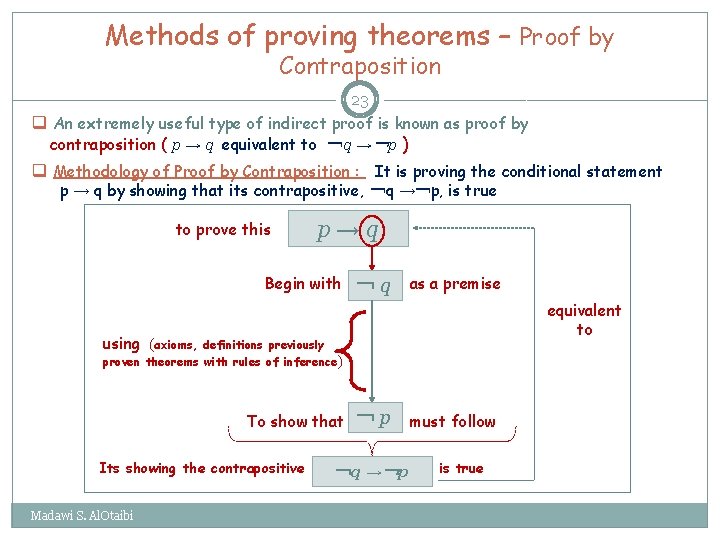
Methods of proving theorems – Proof by Contraposition 23 q An extremely useful type of indirect proof is known as proof by contraposition ( p → q equivalent to ￢q →￢p ) q Methodology of Proof by Contraposition : It is proving the conditional statement p → q by showing that its contrapositive, ￢q →￢p, is true to prove this p→q Begin with ￢q as a premise equivalent to using (axioms, definitions previously proven theorems with rules of inference ) To show that Its showing the contrapositive Madawi S. Al. Otaibi ￢p ￢q →￢p must follow is true

Methods of proving theorems – Proof by Contraposition 24 q Example 6 Prove that if n is an integer and 3 n + 2 is odd, then n is odd. Ø Proof: ~(n is odd) => n is even We assume that the conclusion of the conditional statement “if 3 n + 2 is odd, then n is odd” is false. (Substituting hypothesis) 2 k for n => We assume that n is even. (hypothesis) in hypthesis : 3 n+2 => n = 2 k , where k is some integer. (definition of even number) => 3 n + 2 = 3(2 k) + 2 = 6 k + 2 = 2(3 k + 1) Since r = 3 k + 1 is an integer (Axiom) It is not odd, . This is the (Substituting 2 k for n) negation of the premise of theorem. => 3 n + 2 = 2 r is even. (definition of even number) Because the negation of the conclusion of the conditional statement implies that the hypothesis is false, the original conditional statement is true. We have proved theorem “if 3 n + 2 is odd, then n is odd” Madawi S. Al. Otaibi

Methods of proving theorems – Proof by Contraposition 25 q Example 7 Use an indirect proof to show that “if n 2 is odd then n is odd” Ø Proof: The contraposition is “if n is not odd then n 2 is not odd ” => We Assume that n is not odd i. e. , n is even (hypothesis) => n = 2 k , where k is some integer. (definition of even number) => n 2 = (2 k)2 = 4 k 2 = 2(2 k 2) Since r = 2 k 2 is an integer => n 2 = 2 r Madawi S. Al. Otaibi (Axiom) (definition of not odd number)

Methods of proving theorems – Proof by Contraposition 26 q Q 4 Use an indirect proof to show that “If n is an even integer, then n 2 is even. ” q Example 8 Prove that if n = ab where a and b are positive integers then a n or b n Ø Proof: Let p=“a n”, q=“b n” and r=“n=ab” We want to prove that r p q => The contraposition is (p q ) r (By definition) => p q r (De Morgan’s law) Now, assume that a n and b n ( p q) => a. b n. n = n (by multiplying above twos) => ab n => r which contradicts the statement n = ab Because the negation of the conclusion of the conditional statement implies that the hypothesis is false, the original conditional statement is true. Madawi S. Al. Otaibi

Methods of proving theorems – Vacuous Proofs 27 q Vacuous Proofs A conditional statement p q is TRUE if p is FALSE. If we can show that p is False, then we have a proof, called vacuous proof, of the conditional statement p q. p q F F T T T F T q Example 9 Show that the proposition P(0) is true, where P(n) is “If n > 1, then n 2 > n” and the domain consists of all integers. Ø Proof: Note that P(0) is “If 0 > 1, then 02 > 0. ” We can show P(0) using a vacuous proof. Indeed, the hypothesis 0 > 1 is false. This tells us that P(0) is automatically true. q Example 10 Prove that if he is alive and he is dead then the sun is ice cold Ø Proof: Since the hypothesis is always false the implication is vacuously true. Madawi S. Al. Otaibi

Methods of proving theorems – Trivial Proofs 28 q Trivial Proofs A conditional statement p q is TRUE if q is True. If we can show that q is True, then we have a proof, called Trivial proof, of the conditional statement p q. p q F F T T T F T q Example 11 Let P(n) be “If a and b are positive integers with a ≥ b, then an ≥ bn” where the domain consists of all nonnegative integers. Show that P(0) is true. Ø Proof: The proposition P(0) is “If a ≥ b, then a 0 ≥ b 0. ” Because a 0 = b 0 = 1, the conclusion of the conditional statement “If a ≥ b, then a 0 ≥ b 0” is true. Hence, this conditional statement, which is P(0), is true q Example 12 Prove that if x=2 then x 2 0 for all real numbers Ø Proof: Since x 2 0 is true then the implication is trivially true. (we didn’t use the fact x=2) q Q 5 Use a trivial proof to show that if n > 1 then n 2 ≥ n for all integers Madawi S. Al. Otaibi

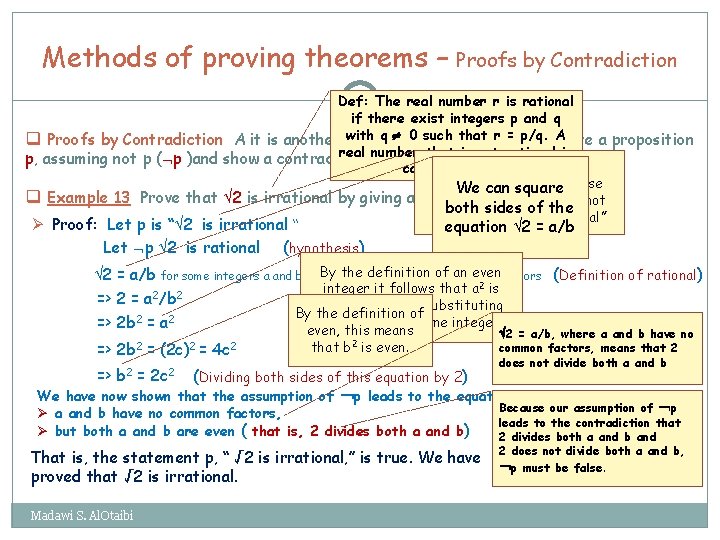
Methods of proving theorems – Proofs by Contradiction 29 The real number r is rational Def: if there exist integers p and q indirect 0 such that r =that p/q. prove A q Proofs by Contradiction A it is another with type qof proof a proposition real number that is not rational is p, assuming not p ( p )and show a contradiction. To start a proof by called irrational contradiction, we suppose We can square q Example 13 Prove that 2 is irrational by giving a proof by contradiction. that ￢p is true , "It is not both sides of the case that is irrational” Ø Proof: Let p is “ 2 is irrational “ equation 2 = a/b Let p 2 is rational (hypothesis) By the an evenfactors (Definition of rational) 2 = a/b for some integers a and b (b 0) and adefinition and b have of no common integer it follows that a 2 is 2 2 => 2 = a /b even, so we can Substituting By the definition of 2 2 with a = 2 c for some integer c => 2 b = a even, this means => 2 b 2 = (2 c)2 => b 2 = 2 c 2 = 4 c 2 that b 2 is even. (Dividing both sides of this equation by 2) 2 = a/b, where a and b have no common factors, means that 2 does not divide both a and b We have now shown that the assumption of ￢p leads to the equation √ 2 = a/b, where Because our assumption of ￢p Ø a and b have no common factors, leads to the contradiction that Ø but both a and b are even ( that is, 2 divides both a and b) 2 divides both a and b and That is, the statement p, “ √ 2 is irrational, ” is true. We have proved that √ 2 is irrational. Madawi S. Al. Otaibi 2 does not divide both a and b, ￢p must be false.

Methods of proving theorems – Proofs by Contradiction 30 q To prove a conditional statement p q by contradiction we prove that: ( p q F is true ) which is equivalent to p q. q Example 14 Give a proof by contradiction of theorem : “If 3 n + 2 is odd, then n is odd. ” Ø Proof: Suppose that 3 n+2 is odd and n is even [p q] => n = 2 r (hypothesis q, definition of even numbers) =>3 n = 6 r (multiply both sides by 3) => 3 n+2=2+6 r (add 2 to both sides) => 3 n+2=2(1+3 r) => 3 n+2=2 k (Let k=1+3 r) => Thus 3 n+2 is even which is false (a contradiction !) Therefore the implication is true. Madawi S. Al. Otaibi

Methods of proving theorems – Proofs of Equivalence 31 q Proofs of Equivalence To prove a theorem that is a biconditional statement, that is, a statement of the form p ↔ q, we show that p → q and q → p are both true. q Example 15 Prove theorem: “If n is an integer, then n is odd if and only if n 2 is odd. ” Ø “if n is odd then n 2 is odd” proved in Example 5 Ø “ n 2 is odd then n is odd” proved in Example 7 Ø Therefore, n is even if and only if n 2 is even q Proving equivalence of several propositions: If we want to prove that p 1 p 2 p 3… pn Ø Then it is sufficient to prove p 1 p 2, , p 2 p 3 … pn p 1 Madawi S. Al. Otaibi

Methods of proving theorems – Counterexample 32 q Counterexample : To show that a statement of the form ∀x. P(x) is false, we need only find a counterexample, that is, an example x for which P(x) is false. Ø E. g. Prove that “For all real numbers x 2 > x” is false X=0. 5 is a counterexample since 0. 52 > 0. 5 is not true q Example 16 Show that the statement: “Every positive integer is the sum of the squares of two integers” is false. Ø To show that this statement is false, we look for a counterexample which is 3 because we cannot write 3 as the sum of the squares of two integers. To show this is the case, note that the only perfect squares not exceeding 3 are: (02 = 0 & 12 = 1), but 3 1+0. Therefore the statement is false Madawi S. Al. Otaibi

Methods of proving theorems – proof by cases 33 q Proof by cases : A proof by cases must cover all possible cases that arise in a theorem. Each case may cover an infinite number of instances q Example 17 Prove "if n is an integer then n 2 ≥ n". Ø Proof: We can prove that n 2 ≥ n for every integer by considering three cases, when n = 0, when n ≥ 1, and when n ≤ -1. Case I: When n = 0, since 02 = 0, 02 >= 0. So, n 2 ≥ n is true. Case II: When n ≥ 1, From n ≥ 1, we get n 2 ≥ n (by multiplying with n). Case III: When n ≤ -1, since n is negative, n 2 is positive, so n 2 ≥ n. Hence, if n is an integer then n 2 ≥ n. q Q 6 Use a trivial Prove that |xy| = |x||y|, where x and y real numbers. Hint: Consider all 4 cases: x and y positive or negative q Common Error with exhaustive proof and proof by cases: Ø Draw conclusion from non-exhaustive examples Ø Not covering all possible cases Madawi S. Al. Otaibi

Methods of proving theorems – proof by cases 34 q Leveraging Proof by cases : look for a proof by cases when there is no obvious way to begin a proof, but when extra information in each case helps move the proof forward. q Example 18 Show that there are no solutions in integers x and y of x 2 + 3 y 2 = 8. Ø Proof: We can quickly reduce a proof to checking just a few simple cases because x 2 > 8 when |x| ≥ 3 and 3 y 2 > 8 when |y| ≥ 2. This leaves the cases when x equals − 2, − 1, 0, 1, or 2 and y equals − 1, 0, or 1. We can finish using an exhaustive proof. To dispense with the remaining cases, we note that possible values for x 2 are 0, 1, and 4, and possible values for 3 y 2 are 0 and 3, and the largest sum of possible values for x 2 and 3 y 2 is 7. it is impossible for x 2 + 3 y 2 = 8 to hold when x and y are integers. Madawi S. Al. Otaibi

Mistakes in Proofs 35 q There are many common errors made in constructing mathematical and the most common errors are mistakes in arithmetic and basic algebra. q Each step of a mathematical proof needs to be correct and the conclusion needs to follow logically from the steps that precede it. Be careful! Many mistakes result from the introduction of steps that do not logically follow from those that precede it Madawi S. Al. Otaibi

Mistakes in Proofs 36 q Example 19 What is wrong with this famous supposed “proof” that 1 = 2 ? Ø Proof: Suppose a and b are two equal positive integers. Steps : Reason 1. a=b 2. a 2 = ab 3. a 2 - b 2 = ab - b 2 4. (a − b)(a + b) = b(a − b) ( Given) The error is that a − b equals zero; of(1) both of an (Multiply bothdivision sides of by sides a) equation by the same quantity is (Subtract b 2 from both sidesquantity of (2)) is valid as long as this zero. (Factor both sides not of (3)) 5. a+b=b (Divide both sides of (4) by a − b ) 6. 2 b = b (Replace a by b in (5) because a = b & simplify) 7. 2= 2 (Divide both sides of (6) by b) Ø Can you find the error Every step is valid except for one, step 5 where we divided both sides by a − b Madawi S. Al. Otaibi

Mistakes in Proofs 37 q Example 20 What is wrong with this “proof” ? “Theorem: ” If n 2 is positive, then n is positive. Ø Proof: Suppose that n 2 is positive. Because the conditional statement : “If n is positive, then n 2 is positive” is true, we can conclude that n is positive. Ø Solution : Let P(n) be “n is positive” and Q(n) be “n 2 is positive. ” Then our hypothesis is Q(n). (1) This statement “If n is positive, then n 2 is positive” is the statement: ∀n(P (n) → Q(n)). (2) From the hypothesis (1) and the statement (2): We cannot conclude P(n) A counterexample because we are not supplied by n rule = − 1 of for using a valid which inference n 2 = 1 is positive, . but n is negative. Instead, we can prove that by using counterexample Madawi S. Al. Otaibi

End of Chapter 3