CS 1020 Data Structures and Algorithms I Lecture

CS 1020 Data Structures and Algorithms I Lecture Note #11 Stacks and Queues Two basic linear data structures

Objectives 1 • Able to define a Stack ADT, and to implement it with array and linked list 2 • Able to define a Queue ADT, and to implement it with array and linked list 3 4 • Able to use stack and queue in applications • Able to use Java API Stack class and Queue interface [CS 1020 Lecture 11: Stacks and Queues] 2

References Book • Stacks: Chapter 7 (recursion excluded) • Queues: Chapter 8 CS 1020 website Resources Lectures • http: //www. comp. nus. edu. sg/ ~cs 1020/2_resources/lectures. html [CS 1020 Lecture 11: Stacks and Queues] 3

Programs used in this lecture n Stacks q q q n Queues q q n Stack. ADT. java, Stack. Arr. java, Stack. LL. java, Stack. LLE. java Test. Stack. java Postfix. java, Prefix. java Queue. ADT. java, Queue. Arr. java, Queue. LL. java, Queue. LLE. java Test. Queue. java Application q Palindromes. java [CS 1020 Lecture 11: Stacks and Queues] 4

Outline 1. 2. 3. 4. 5. Stack ADT (Motivation) Stack Implementation via Array Stack Implementation via Linked List java. util. Stack <E> Stack Applications § Bracket matching § Postfix calculation 6. Queue ADT (Motivation) 7. Queue Implementation via Array 8. Queue Implementation via Tailed Linked List 9. java. util. interface Queue <E> 10. Application: Palindromes [CS 1020 Lecture 11: Stacks and Queues] 5

1 -5 Stacks Last-In-First-Out (LIFO)

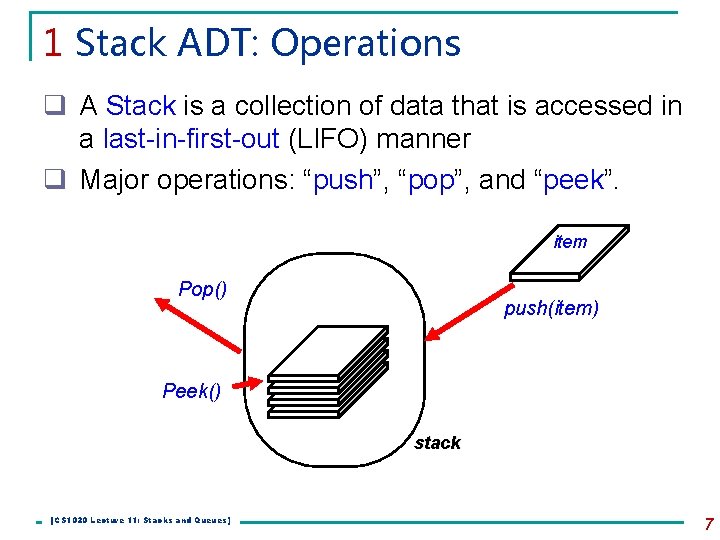
1 Stack ADT: Operations q A Stack is a collection of data that is accessed in a last-in-first-out (LIFO) manner q Major operations: “push”, “pop”, and “peek”. item Pop() push(item) Peek() stack [CS 1020 Lecture 11: Stacks and Queues] 7

1 Stack ADT: Uses q Calling a function § Before the call, the state of computation is saved on the stack so that we will know where to resume q Recursion q Matching parentheses q Evaluating arithmetic expressions (e. g. a + b – c) : § § postfix calculation Infix to postfix conversion q Traversing a maze [CS 1020 Lecture 11: Stacks and Queues] 8

1 Stack ADT: Interface import java. util. *; Stack. ADT. java public interface Stack. ADT <E> { // check whether stack is empty public boolean empty(); // retrieve topmost item on stack public E peek() throws Empty. Stack. Exception; // remove and return topmost item on stack public E pop() throws Empty. Stack. Exception; // insert item onto stack public void push(E item); } [CS 1020 Lecture 11: Stacks and Queues] 9

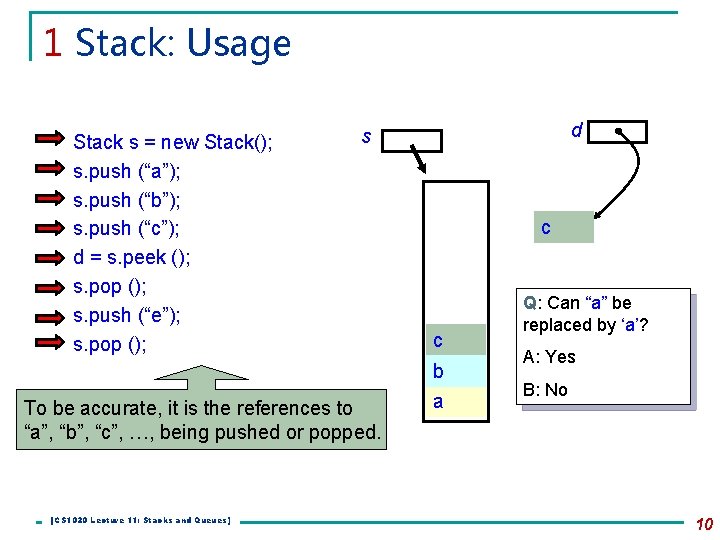
1 Stack: Usage Stack s = new Stack(); s. push (“a”); s. push (“b”); s. push (“c”); d = s. peek (); s. pop (); s. push (“e”); s. pop (); To be accurate, it is the references to “a”, “b”, “c”, …, being pushed or popped. [CS 1020 Lecture 11: Stacks and Queues] d s c c e b a Q: Can “a” be replaced by ‘a’? A: Yes B: No 10

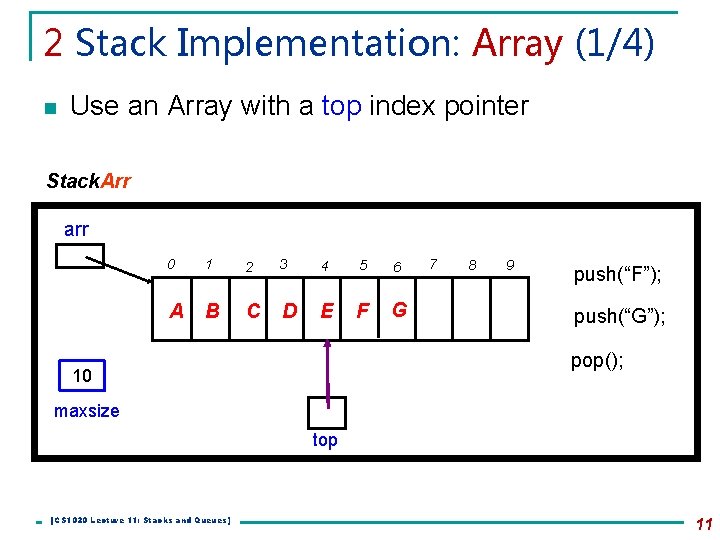
2 Stack Implementation: Array (1/4) n Use an Array with a top index pointer Stack. Arr arr 0 1 2 3 4 5 6 A B C D E F G 7 8 9 push(“F”); push(“G”); pop(); 10 maxsize top [CS 1020 Lecture 11: Stacks and Queues] 11

2 Stack Implementation: Array (2/4) import java. util. *; Stack. Arr. java class Stack. Arr <E> implements Stack. ADT <E> { private E[] arr; private int top; private int max. Size; private final int INITSIZE = 1000; public Stack. Arr() { arr = (E[]) new Object[INITSIZE]; // creating array of type E top = -1; // empty stack - thus, top is not on an valid array element max. Size = INITSIZE; } public boolean empty() { return (top < 0); } [CS 1020 Lecture 11: Stacks and Queues] 12

2 Stack Implementation: Array (3/4) n pop() reuses peek() Stack. Arr. java public E peek() throws Empty. Stack. Exception { if (!empty()) return arr[top]; else throw new Empty. Stack. Exception(); } public E pop() throws Empty. Stack. Exception { E obj = peek(); top--; return obj; } [CS 1020 Lecture 11: Stacks and Queues] 13

2 Stack Implementation: Array (4/4) push() needs to consider overflow n Stack. Arr. java public void push(E obj) { if (top >= max. Size - 1) enlarge. Arr(); //array is full, enlarge it top++; arr[top] = obj; private } method private void enlarge. Arr() { // When there is not enough space in the array // we use the following method to double the number // of entries in the array to accommodate new entry int new. Size = 2 * max. Size; E[] x = (E[]) new Object[new. Size]; for (int j=0; j < max. Size; j++) { x[j] = arr[j]; } max. Size = new. Size; arr = x; } } [CS 1020 Lecture 11: Stacks and Queues] 14

3 Stack Implementation: Linked List (1/6) n A class can be defined in 2 ways: via composition: class A { B b = new B (…); // A is composed of instance of B … } via inheritance: class A extends B { // A is an extension of B …. } [CS 1020 Lecture 11: Stacks and Queues] 15

Recall: List. Node (last week) class List. Node <E> { /* data attributes */ private E element; private List. Node <E> next; List. Node. java element next /* constructors */ public List. Node(E item) { this(item, null); } public List. Node(E item, List. Node <E> n) { element = item; next = n; } /* get the next List. Node */ public List. Node <E> get. Next() { return next; } /* get the element of the List. Node */ public E get. Element() { return element; } /* set the next reference */ public void set. Next(List. Node <E> n) { next = n }; } [CS 1020 Lecture 11: Stacks and Queues] 16

Recall: Basic Linked List (1/2) (last week) Basic. Linked. List. java import java. util. *; class Basic. Linked. List <E> implements List. Interface <E> { private List. Node <E> head = null; private int num_nodes = 0; public boolean is. Empty() { return (num_nodes == 0); } public int size() { return num_nodes; } public E get. First() throws No. Such. Element. Exception { if (head == null) throw new No. Such. Element. Exception("can't get from an empty list"); else return head. get. Element(); } public boolean contains(E item) { for (List. Node <E> n = head; n != null; n = n. get. Next()) if (n. get. Element(). equals(item)) return true; return false; } [CS 1020 Lecture 11: Stacks and Queues] 17

Recall: Basic Linked List (2/2) (last week) public void add. First(E item) { head = new List. Node <E> (item, head); num_nodes++; } Basic. Linked. List. java public E remove. First() throws No. Such. Element. Exception { List. Node <E> ln; if (head == null) throw new No. Such. Element. Exception("can't remove from empty list"); else { ln = head; head = head. get. Next(); num_nodes--; return ln. get. Element(); } public void print() throws No. Such. Element. Exception { //. . . Code omitted } } [CS 1020 Lecture 11: Stacks and Queues] 18

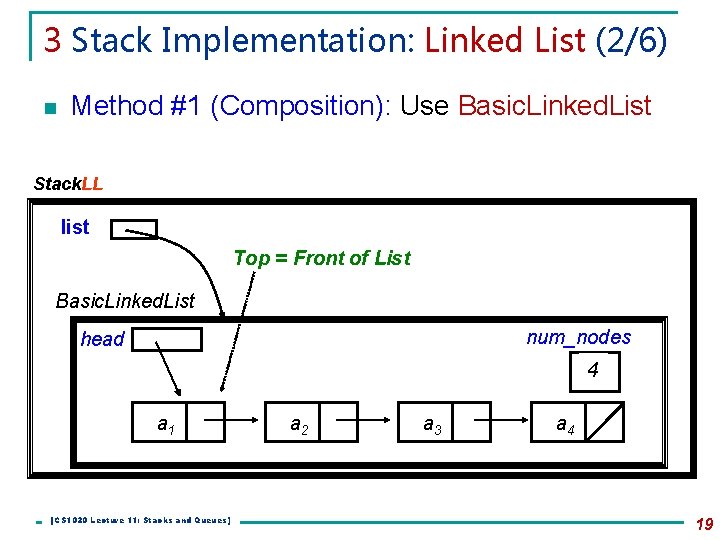
3 Stack Implementation: Linked List (2/6) n Method #1 (Composition): Use Basic. Linked. List Stack. LL list Top = Front of List Basic. Linked. List num_nodes head 4 a 1 [CS 1020 Lecture 11: Stacks and Queues] a 2 a 3 a 4 19

3 Stack Implementation: Linked List (3/6) n Method #1 (Composition): Use Basic. Linked. List import java. util. *; Stack. LL. java class Stack. LL <E> implements Stack. ADT <E> { private Basic. Linked. List <E> list; // Why private? public Stack. LL() { list = new Basic. Linked. List <E> (); } public boolean empty() { return list. is. Empty(); } public E peek() throws Empty. Stack. Exception { try { return list. get. First(); } catch (No. Such. Element. Exception e) { throw new Empty. Stack. Exception(); } } [CS 1020 Lecture 11: Stacks and Queues] 20

3 Stack Implementation: Linked List (4/6) n Method #1 (Composition): Use Basic. Linked. List public E pop() throws Empty. Stack. Exception { E obj = peek(); list. remove. First(); return obj; } Stack. LL. java public void push(E o) { list. add. First(o); } } Notes: 1. is. Empty(), get. First(), remove. First(), and add. First() are public methods of Basic. Linked. List. 2. No. Such. Element. Exception is thrown by get. First() or remove. First() of Basic. Linked. List. [CS 1020 Lecture 11: Stacks and Queues] 21

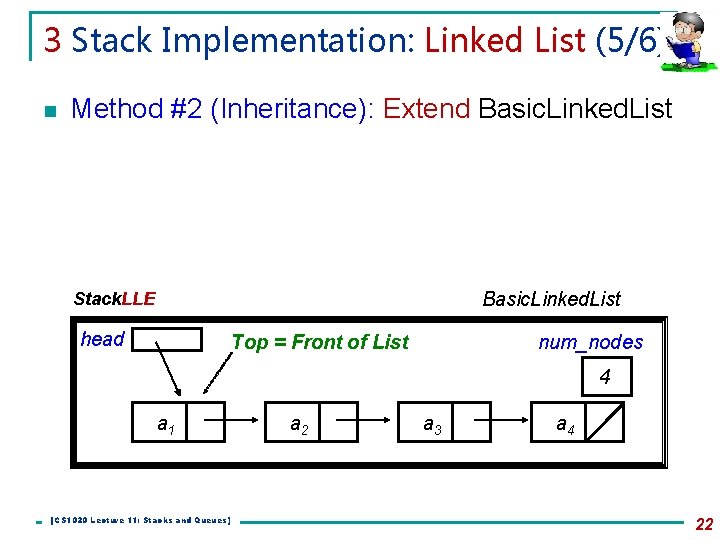
3 Stack Implementation: Linked List (5/6) n Method #2 (Inheritance): Extend Basic. Linked. List Stack. LLE head num_nodes Top = Front of List 4 a 1 [CS 1020 Lecture 11: Stacks and Queues] a 2 a 3 a 4 22

3 Stack Implementation: Linked List (6/6) n Method #2 (Inheritance): Extend Basic. Linked. List import java. util. *; Stack. LLE. java class Stack. LLE <E> extends Basic. Linked. List <E> implements Stack. ADT <E> { public boolean empty() { return is. Empty(); } public E peek() throws Empty. Stack. Exception { try { return get. First(); } catch (No. Such. Element. Exception e) { throw new Empty. Stack. Exception(); } } public E pop() throws Empty. Stack. Exception { E obj = peek(); remove. First(); return is. Empty(); } public void push (E o) { add. First(o); } } [CS 1020 Lecture 11: Stacks and Queues] 23

3 Uses of Stack import java. util. *; public class Test. Stack { public static void main (String[] args) { Test. Stack. java // You can use any of the following 4 implementations of Stack. Arr <String> stack = new Stack. Arr <String>(); // Array //Stack. LL <String> stack = new Stack. LL <String>(); // Linked. List composition //Stack. LLE <String> stack = new Stack. LLE <String>(); // Linked. List inheritance //Stack <String> stack = new Stack <String>(); // Java API System. out. println("stack is empty? stack. push("1"); stack. push("2"); System. out. println("top of stack is stack. push("3"); System. out. println("top of stack is stack. push("4"); stack. pop(); System. out. println("top of stack is " + stack. empty()); " + stack. peek()); " + stack. pop()); " + stack. peek()); } } [CS 1020 Lecture 11: Stacks and Queues] 24

4 java. util. Stack <E> (1/2) Note: The method “int search (Object o)” is not commonly known to be available from a Stack. [CS 1020 Lecture 11: Stacks and Queues] 25

4 java. util. Stack <E> (2/2) [CS 1020 Lecture 11: Stacks and Queues] 26

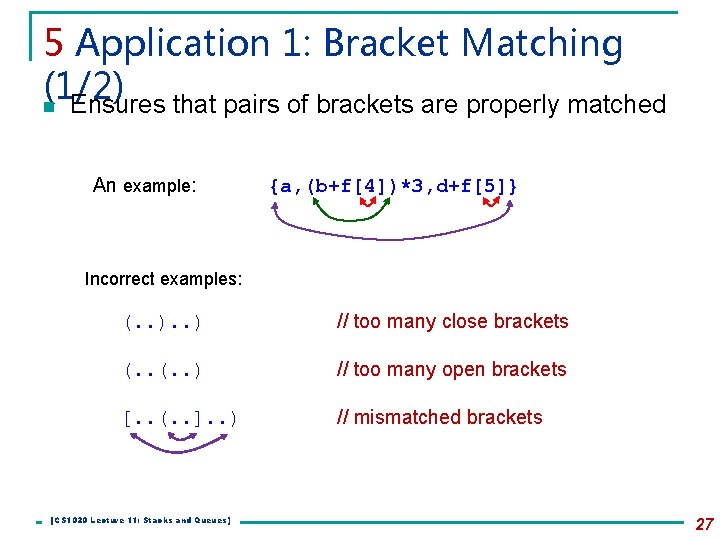
5 Application 1: Bracket Matching (1/2) n Ensures that pairs of brackets are properly matched An example: {a, (b+f[4])*3, d+f[5]} Incorrect examples: (. . ) // too many close brackets (. . ) // too many open brackets [. . (. . ]. . ) // mismatched brackets [CS 1020 Lecture 11: Stacks and Queues] 27

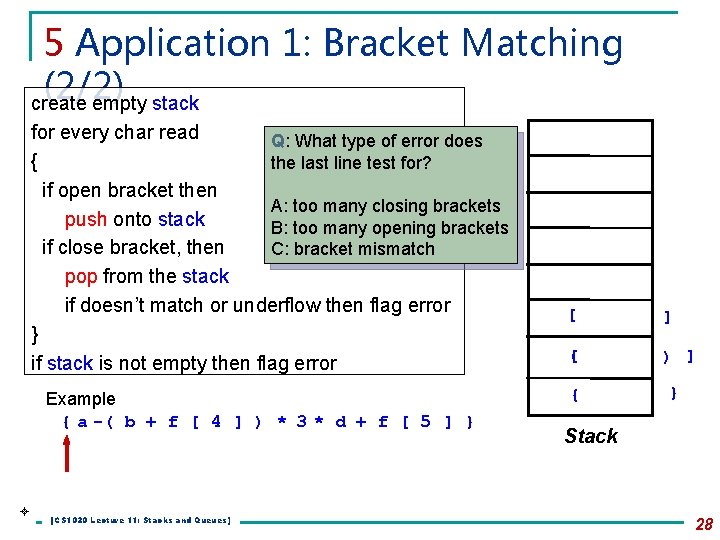
5 Application 1: Bracket Matching (2/2) create empty stack for every char read Q: What type of error does { the last line test for? if open bracket then A: too many closing brackets push onto stack B: too many opening brackets if close bracket, then C: bracket mismatch pop from the stack if doesn’t match or underflow then flag error } if stack is not empty then flag error Example { a -( b + f [ 4 ] ) * 3 * d + f [ 5 ] } [CS 1020 Lecture 11: Stacks and Queues] [ ] ( [ ) ] { } Stack 28

5 Applicn 2: Arithmetic Expression (1/7) n Terms q q q n Expression: Operands: Operators: a = b + c * d a, b, c, d =, +, –, *, /, % Precedence rules: Operators have priorities over one another as indicated in a table (which can be found in most books & our first few lectures) q q Example: * and / have higher precedence over + and –. For operators at the same precedence (such as * and /), we process them from left to right [CS 1020 Lecture 11: Stacks and Queues] 29

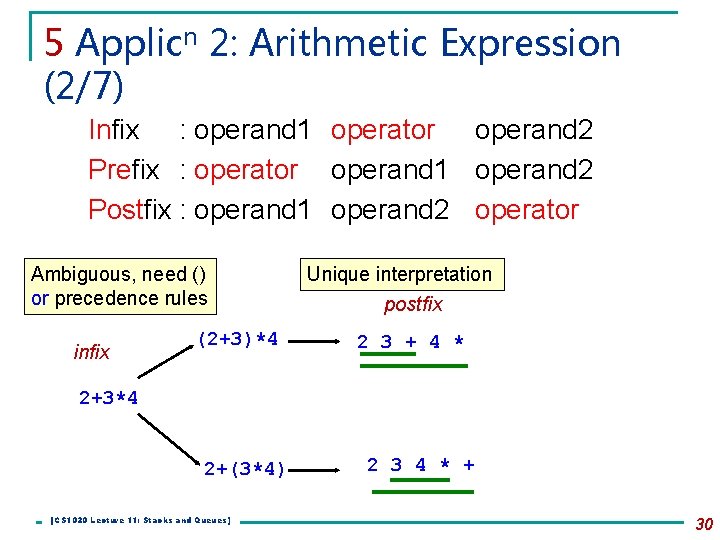
5 Applicn 2: Arithmetic Expression (2/7) Infix : operand 1 operator operand 2 Prefix : operator operand 1 operand 2 Postfix : operand 1 operand 2 operator Ambiguous, need () or precedence rules infix (2+3)*4 Unique interpretation postfix 2 3 + 4 * 2+3*4 2+(3*4) [CS 1020 Lecture 11: Stacks and Queues] 2 3 4 * + 30

5 Applicn 2: Arithmetic Expression (3/7) Algorithm: Calculating Postfix expression with stack Create an empty stack for each item of the expression, if it is an operand, push it on the stack if it is an operator, pop arguments from stack; perform the operation; push the result onto the stack Infix postfix 2 * (3 + 4) Stack arg 1 32 arg 2 47 [CS 1020 Lecture 11: Stacks and Queues] 2 3 4 + * s. push(2) s. push(3) s. push(4) arg 2 = s. pop () arg 1 = s. pop () s. push (arg 1 + arg 2) * arg 2 = s. pop () arg 1 = s. pop () s. push (arg 1 * arg 2) 2 3 4 + 4 3 7 2 14 31

5 Applicn 2: Arithmetic Expression (4/7) Brief steps for Infix to Postfix Conversion 1. 2. 3. 4. Scan infix expression from left to right If an operand is found, add it to the postfix expression. If a “(” is found, push it onto the stack. If a “)” is found a) repeatedly pop the stack and add the popped operator to the postfix expression until a “(” is found. b) remove the “(”. 5. If an operator is found a) repeatedly pop the operator from stack which has higher or equal precedence than/to the operator found, and add the popped operator to the postfix expression. b) add the new operator to stack 6. If no more token in the infix expression, repeatedly pop the operator from stack and add it to the postfix expression. [CS 1020 Lecture 11: Stacks and Queues] 32

5 Applicn 2: Arithmetic Expression Algorithm: Converting Infix to an equivalent Postfix (5/7) String postfix. Exp = ""; for (each character ch in the infix expression) { switch (ch) { case operand: postfix. Exp = postfix. Exp + ch; break; case '(': stack. push(ch); break; case ')': while ( stack. peek() != '(' ) postfix. Exp = postfix. Exp + stack. pop(); break; // remove '(' case operator: while ( !stack. empty() && stack. peek() != '(' && precedence(ch) <= precedence(stack. peek()) ) // Why “<=”? postfix. Exp = postfix. Exp + stack. pop(); stack. push(ch); break; } // end switch } // end for while ( !stack. empty() ) postfix. Exp = postfix. Exp + stack. pop(); [CS 1020 Lecture 11: Stacks and Queues] 33

5 Applicn 2: Arithmetic Expression (6/7) Algorithm: Converting Infix to an equivalent Postfix ch a – ( b + c * d ) / e Stack (bottom to top) – – ( – ( + * – ( + – ( – – / [CS 1020 Lecture 11: Stacks and Queues] postfix. Exp a a b a b c d a b c d * + a b c d * + e / – Example: a – ( b + c * d ) / e Move operators from stack to postfix. Exp until '(' Copy remaining operators from stack to postfix. Exp 34

5 Applicn 2: Arithmetic Expression (7/7) n How to code the above algorithm in Java? q q n Complete Postfix. Incomplete. java Answer in subdirectory “/answers”, but try it out yourself first. How to do conversion of infix to prefix? q See Prefix. java [CS 1020 Lecture 11: Stacks and Queues] 35

6 -9 Queues First-In-First-Out (FIFO)

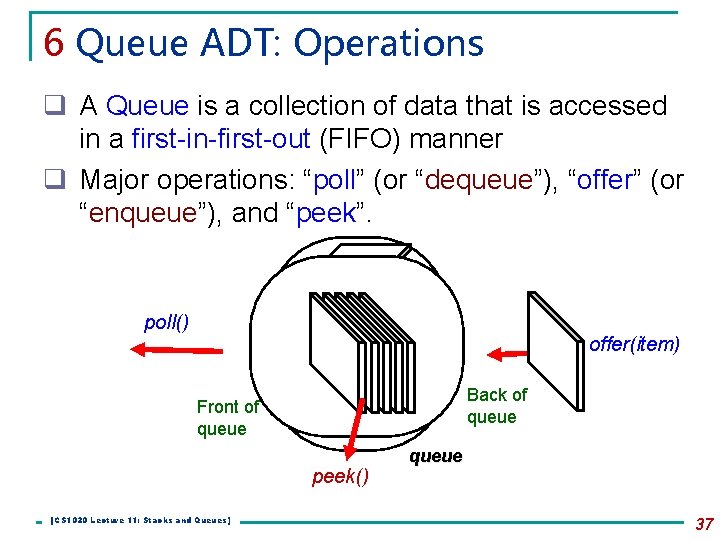
6 Queue ADT: Operations q A Queue is a collection of data that is accessed in a first-in-first-out (FIFO) manner q Major operations: “poll” (or “dequeue”), “offer” (or “enqueue”), and “peek”. poll() offer(item) Back of queue Front of queue peek() [CS 1020 Lecture 11: Stacks and Queues] queue 37

6 Queue ADT: Uses q Print queue q Simulations q Breadth-first traversal of trees q Checking palindromes - for illustration only as it is not a real application of queue [CS 1020 Lecture 11: Stacks and Queues] 38

6 Queue ADT: Interface import java. util. *; Queue. ADT. java public interface Queue. ADT <E> { // return true if queue has no elements public boolean is. Empty(); // return the front of the queue public E peek(); // remove and return the front of the queue public E poll(); // also commonly known as dequeue // add item to the back of the queue public boolean offer(E item); // also commonly known as enqueue } [CS 1020 Lecture 11: Stacks and Queues] 39

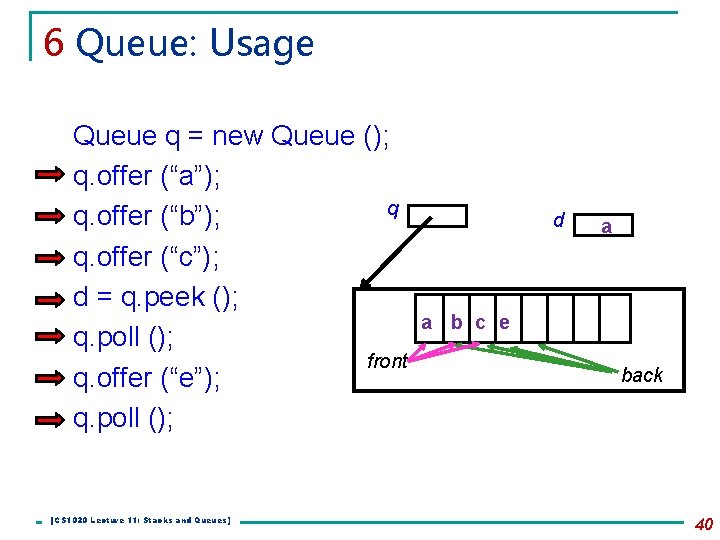
6 Queue: Usage Queue q = new Queue (); q. offer (“a”); q q. offer (“b”); q. offer (“c”); d = q. peek (); q. poll (); front q. offer (“e”); q. poll (); [CS 1020 Lecture 11: Stacks and Queues] d a a b c e back 40

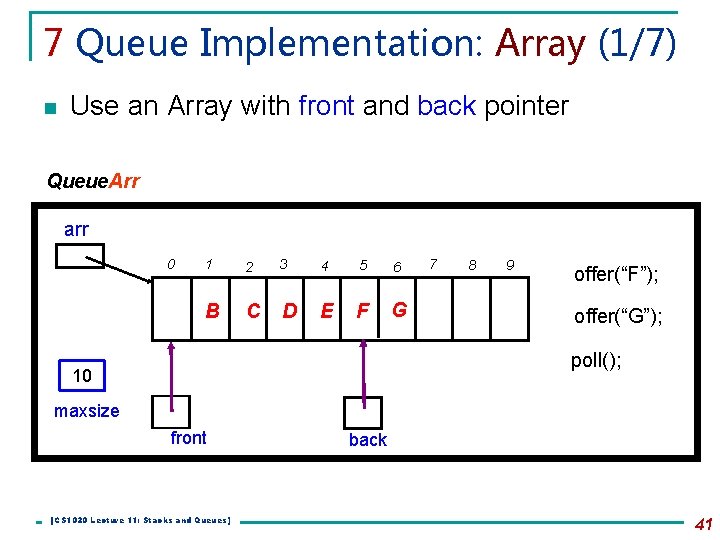
7 Queue Implementation: Array (1/7) n Use an Array with front and back pointer Queue. Arr arr 0 1 2 3 4 5 6 A B C D E F G 7 8 9 offer(“F”); offer(“G”); poll(); 10 maxsize front [CS 1020 Lecture 11: Stacks and Queues] back 41

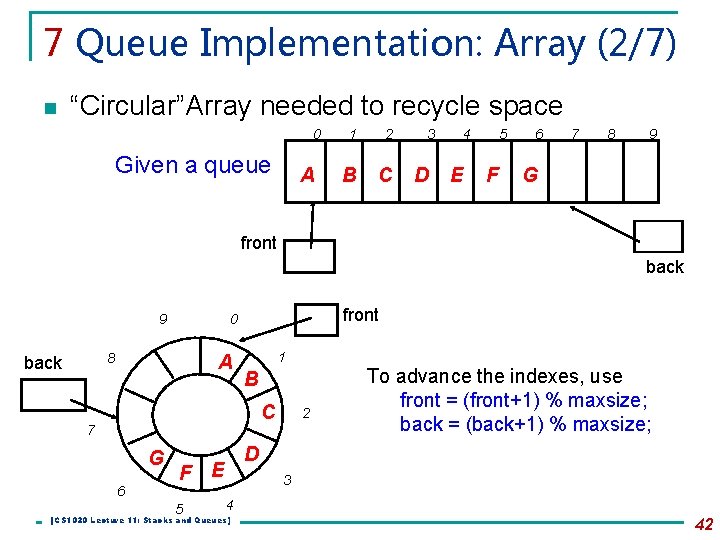
7 Queue Implementation: Array (2/7) n “Circular”Array needed to recycle space 0 Given a queue A 1 2 B C 3 D 4 E 5 F 6 7 8 9 G front back 8 back front 0 9 A 1 B C 7 G 6 D F E 5 2 To advance the indexes, use front = (front+1) % maxsize; back = (back+1) % maxsize; 3 4 [CS 1020 Lecture 11: Stacks and Queues] 42

7 Queue Implementation: Array (3/7) n Question: what does (front == back) mean? A: Full queue B: Empty queue C: Both A and B D: Neither A nor B [CS 1020 Lecture 11: Stacks and Queues] 43

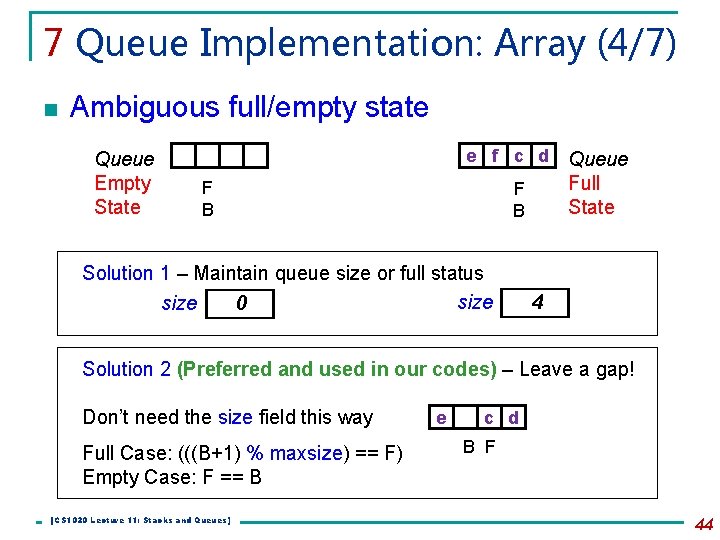
7 Queue Implementation: Array (4/7) n Ambiguous full/empty state Queue Empty State e f c d F B Solution 1 – Maintain queue size or full status size 0 size Queue Full State 4 Solution 2 (Preferred and used in our codes) – Leave a gap! Don’t need the size field this way Full Case: (((B+1) % maxsize) == F) Empty Case: F == B [CS 1020 Lecture 11: Stacks and Queues] e c d B F 44

7 Queue Implementation: Array (5/7) Queue. Arr. java import java. util. *; // This implementation uses solution 2 to resolve full/empty state class Queue. Arr <E> implements Queue. ADT <E> { private E [] arr; private int front, back; private int max. Size; private final int INITSIZE = 1000; public Queue. Arr() { arr = (E []) new Object[INITSIZE]; // create array of E objects front = 0; // the queue is empty back = 0; max. Size = INITSIZE; } public boolean is. Empty() { return (front == back); } [CS 1020 Lecture 11: Stacks and Queues] // use solution 2 45

7 Queue Implementation: Array (6/7) public E peek() { // return the front of the queue if (is. Empty()) return null; else return arr[front]; } Queue. Arr. java public E poll() { // remove and return the front of the queue if (is. Empty()) return null; E obj = arr[front]; arr[front] = null; front = (front + 1) % max. Size; // “circular” array return obj; } public boolean offer(E o) { // add item to the back of the queue if (((back+1)%max. Size) == front) // array is full if (!enlarge. Arr()) return false; // no more memory to // enlarge the array arr[back] = o; back = (back + 1) % max. Size; return true; // “circular” array } [CS 1020 Lecture 11: Stacks and Queues] 46

7 Queue Implementation: Array (7/7) private method Queue. Arr. java private boolean enlarge. Arr() { int new. Size = max. Size * 2; E[] x = (E []) new Object[new. Size]; if (x == null) // i. e. no memory allocated to array of E objects return false; for (int j=0; j < max. Size; j++) { // copy the front (1 st) element, 2 nd element, . . . , in the // original array to the 1 st (index 0), 2 nd (index 1), . . . , // positions in the enlarged array. Q: Why this way? x[j] = arr[(front+j) % max. Size]; } front = 0; back = max. Size - 1; arr = x; max. Size = new. Size; return true; } } [CS 1020 Lecture 11: Stacks and Queues] 47

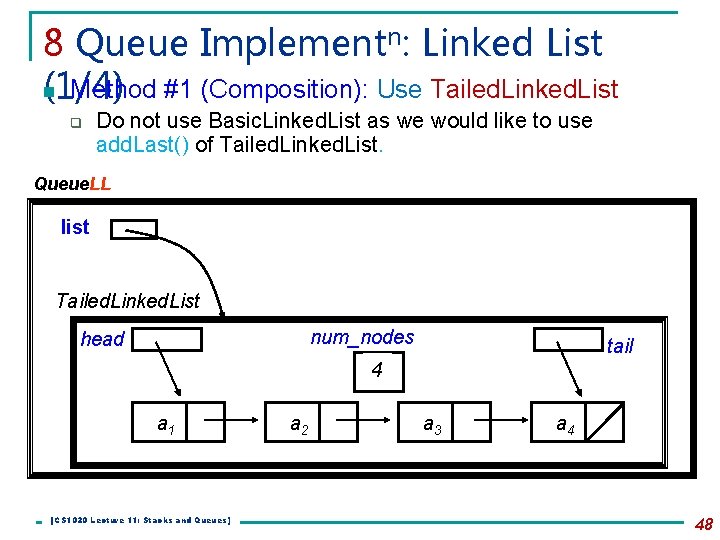
8 Queue Implementn: Linked List n Method #1 (Composition): Use Tailed. Linked. List (1/4) q Do not use Basic. Linked. List as we would like to use add. Last() of Tailed. Linked. List. Queue. LL list Tailed. Linked. List num_nodes head tail 4 a 1 [CS 1020 Lecture 11: Stacks and Queues] a 2 a 3 a 4 48

8 Queue Implementn: Linked List n Method #1 (Composition): Use Tailed. Linked. List (2/4) Queue. LL. java import java. util. *; class Queue. LL <E> implements Queue. ADT <E> { private Tailed. Linked. List <E> list; public Queue. LL() { list = new Tailed. Linked. List <E> (); } public boolean is. Empty() { return list. is. Empty(); } public boolean offer(E o) { list. add. Last(o); // is. Empty(), add. Last(), get. First(), remove. First() // are public methods of Tailed. Linked. List return true; } public E peek() { if (is. Empty()) return null; return list. get. First(); } public E poll() { E obj = peek(); if (!is. Empty()) list. remove. First(); return obj; } } [CS 1020 Lecture 11: Stacks and Queues] 49

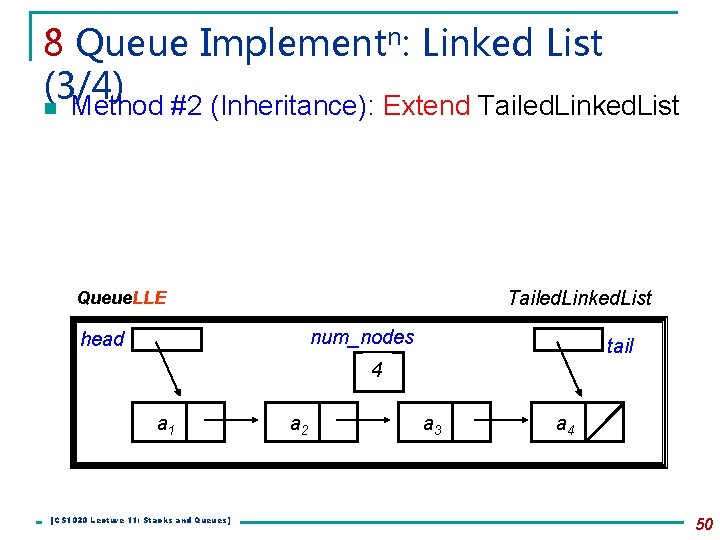
8 Queue Implementn: Linked List (3/4) n Method #2 (Inheritance): Extend Tailed. Linked. List Queue. LLE num_nodes head tail 4 a 1 [CS 1020 Lecture 11: Stacks and Queues] a 2 a 3 a 4 50

8 Queue Implementn: Linked List (4/4) n Method #2 (Inheritance): Extend Tailed. Linked. List import java. util. *; Queue. LLE. java class Queue. LLE <E> extends Tailed. Linked. List <E> implements Queue. ADT <E> { public boolean offer(E o) { add. Last(o); return true; } public E peek() { if (is. Empty()) return null; return get. First(); } public E poll() { E obj = peek(); if (!is. Empty()) remove. First(); return obj; } } [CS 1020 Lecture 11: Stacks and Queues] 51

8 Uses of Queues (1/2) Test. Queue. java import java. util. *; public class Test. Stack { public static void main (String[] args) { // you can use any one of the following implementations //Queue. Arr <String> queue= new Queue. Arr <String> (); // Array Queue. LL <String> queue= new Queue. LL <String> (); // Linked. List composition //Queue. LLE <String> queue= new Queue. LLE <String> (); // Linked. List inheritance System. out. println("queue is empty? " + queue. is. Empty()); queue. offer("1"); System. out. println("operation: queue. offer("1")"); System. out. println("queue is empty? " + queue. is. Empty()); System. out. println("front now is: " + queue. peek()); queue. offer("2"); System. out. println("operation: queue. offer("2")"); System. out. println("front now is: " + queue. peek()); queue. offer("3"); System. out. println("operation: queue. offer("3")"); System. out. println("front now is: " + queue. peek()); [CS 1020 Lecture 11: Stacks and Queues] 52

8 Uses of Queues (2/2) Test. Queue. java queue. poll(); System. out. println("operation: queue. poll()"); System. out. println("front now is: " + queue. peek()); System. out. print("checking whether queue. peek(). equals("1"): "); System. out. println(queue. peek(). equals("1")); queue. poll(); System. out. println("operation: queue. poll()"); System. out. println("front now is: " + queue. peek()); } } [CS 1020 Lecture 11: Stacks and Queues] 53

9 java. util. interface Queue <E> Note: The methods “E element()” and “E remove()” are not in our own Queue ADT. [CS 1020 Lecture 11: Stacks and Queues] 54

10 Palindromes Application using both Stack and Queue

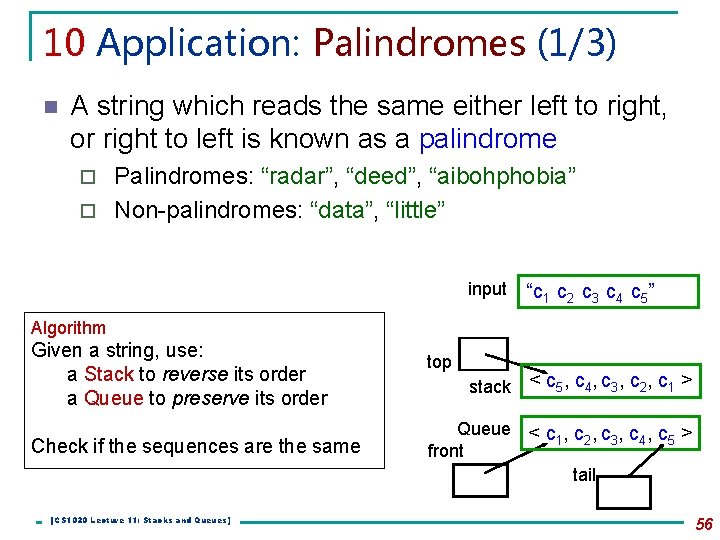
10 Application: Palindromes (1/3) n A string which reads the same either left to right, or right to left is known as a palindrome Palindromes: “radar”, “deed”, “aibohphobia” ¨ Non-palindromes: “data”, “little” ¨ input “c 1 c 2 c 3 c 4 c 5” Algorithm Given a string, use: a Stack to reverse its order a Queue to preserve its order Check if the sequences are the same [CS 1020 Lecture 11: Stacks and Queues] top stack < c 5, c 4, c 3, c 2, c 1 > Queue < c , c , c > 1 2 3 4 5 front tail 56

10 Application: Palindromes (2/3) import java. util. *; public class Palindromes { Palindromes. java public static void main (String[] args) throws No. Such. Element. Exception { // you can use any of the following stack/queue implementations // and Java classes Stack and Linked. List //Stack. LLE <String> stack = new Stack. LLE <String> (); Stack <String> stack = new Stack <String> (); // Stack is a Java class //Stack. LL <String> stack = new Stack. LL <String> (); //Stack. Arr <String> stack = new Stack. Arr <String> (); //Queue. LL <String> queue = new Queue. LL <String> (); //Queue. LLE <String> queue = new Queue. LLE <String> (); //Queue. Arr <String> queue = new Queue. Arr <String> (); Linked. List <String> queue = new Linked. List <String> (); Scanner scanner = new Scanner(System. in); System. out. print("Enter text: "); String input. Str = scanner. next(); for (int i=0; i < input. Str. length(); i++) { String ch = input. Str. substring(i, i+1); stack. push(ch); queue. offer(ch); } [CS 1020 Lecture 11: Stacks and Queues] Linked. List is a Java class that implements interface Queue and other interfaces, such as Serializable, Cloneable, Iterable<E>, Collection<E>, Deque<E>, List<E>. 57

10 Application: Palindromes (3/3) boolean ans = true; try { while (!stack. is. Empty() && ans) { if (!(stack. pop(). equals(queue. poll()))) ans = false; } } catch (No. Such. Element. Exception e) { throw new No. Such. Element. Exception(); } Palindromes. java System. out. print(input. Str + " is "); if (ans) System. out. println("a palindrome"); else System. out. println("NOT a palindrome"); } } [CS 1020 Lecture 11: Stacks and Queues] 58

11 Summary n We learn to create our own data structures from array and linked list q q n LIFO vs FIFO – a simple difference that leads to very different applications Drawings can often help in understanding the cases still Please do not forget that the Java Library class is much more comprehensive than our own – for sit-in lab or exam, please use the one as told. [CS 1020 Lecture 11: Stacks and Queues] 59

End of file