CS 100 J Lecture 5 n Previous Lecture

CS 100 J Lecture 5 n Previous Lecture – Programming Concepts n Rules of thumb – – n learn and use patterns inspiration from hand-working problem boundary conditions validation Pattern for processing input values up to (but not including) a stopping signal – Example n Processing exam grades – Java Constructs n Casts and Rounding – Reading, Lewis & Loftus, Section 3. 9 n This Lecture – Programming Concepts n Programming by stepwise refinement – – n CS 100 a pattern sequential refinement case analysis iterative refinement Use of comments as higher-level statements Lecture 5 1

Programming By Stepwise Refinement n An “algorithm” for you to follow when writing a program that solves problem P: if ( P is simple enough to code immediately ) Write the code that solves P; else { Refine P into subproblems; Write the code that solves each subproblem; } n Stepwise refinement is an example of – a divide-and-conquer algorithm, because it breaks problems down into simpler parts, – a recursive algorithm, because you use the same “algorithm” to write the code for any given subproblem. n The refinement of P into subproblems must include a description of how the code segments solving the subproblems combine to form code that solves P. n You can write the code segments that solve the subproblems in any order. CS 100 Lecture 5 2

Ways to Refine P into Subproblems n A program pattern – Do whatever n times – Process input values up until (but not including) a stopping value. n n n A sequential refinement A case analysis An iterative refinement CS 100 Lecture 5 3

Sequential Refinement n The refinement is structured so that solving P 1 through Pn in sequence solves P. /* Solve problem P */ { /* Solve subproblem P 1 */. . . /* Solve subproblem P 2 */. . . /* Solve subproblem Pn */. . . } CS 100 Lecture 5 4

Sequential Refinement, cont. n Example 1: /* Drive from Ithaca to NYC. */ { /* Drive from Ithaca to Binghamton */. . . /* Drive from Binghamton to NYC */. . . } n Example 2: /* Drive from Ithaca to NYC. */ { /* Drive from Ithaca to Albany. */. . . /* Drive from Albany to NYC. */. . . } CS 100 Lecture 5 5

Sequential Refinement, cont. n Example 1, continued /* Drive from Ithaca to NYC. */ { /* Drive from Ithaca to Binghamton. */. . . /* Drive from Binghamton to NYC. */ /* Drive from Binghamton to Stroudsburg. */. . . /* Drive from Stroudsburg to NYC. */. . . } CS 100 Lecture 5 6

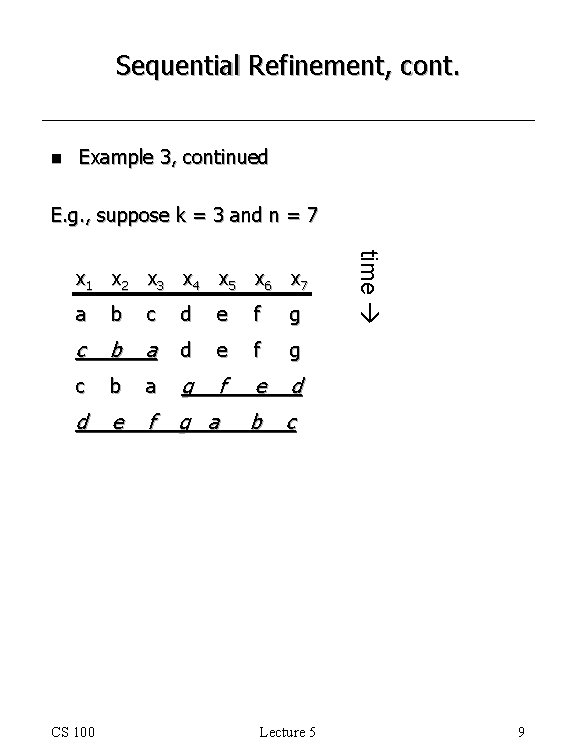
Sequential Refinement, cont. n Example 3 Let X 1, …, Xn be an ordered sequence of variables. Let k be an integer between 1 and n. /* Rotate the values in X 1, …, Xn left k places, where values shifted off the left end reenter at the right. */ E. g. , suppose k = 3, n = 7, and the x’s contain letters. Before: x 1 x 2 x 3 x 4 x 5 x 6 x 7 a b c d e f g After: x 1 x 2 x 3 x 4 x 5 x 6 x 7 d CS 100 e f g a b c Lecture 5 7

Sequential Refinement, cont. /* Rotate the values in X 1, …, Xn left k places, where values shifted off the left end reenter at the right. */ { /* Reverse the order of X 1, …, Xk */. . . /* Reverse the order of Xk+1, …, Xn */. . . /* Reverse the order of X 1, …, Xn */. . . } CS 100 Lecture 5 8

Sequential Refinement, cont. n Example 3, continued E. g. , suppose k = 3 and n = 7 a b c d e f g c b a g f e d d e f g a b c CS 100 Lecture 5 time x 1 x 2 x 3 x 4 x 5 x 6 x 7 9

Case Analysis n The refinement is structured so that solving one of the subproblems P 1, …, Pn solves P. Which Pi is solved is determined during execution by testing conditions. /* Solve problem P */ if (P is an instance of case 1) /* Solve subproblem 1 */. . . else if (P is an instance of case 2) /* Solve subproblem 2 */. . . else if (P is an instance of case 3) /* Solve subproblem 3 */. . . else /* P is an instance of case n */ /* Solve subproblem n */. . . CS 100 Lecture 5 10

Case Analysis, cont. n Example 1 /* Let x be the absolute value of y. */ if ( y < 0 ) /* Let x be -y. */. . . else /* Let x be y. */. . . n Example 2 /* Let x be the absolute value of y. */ x = Math. abs(y); I. e. , sometimes case analysis is counter-productive and there is a uniform way to solve the problem. CS 100 Lecture 5 11

Iterative Refinement n The refinement of P is structured so that repeated solution of subproblem P’ eventually solves P. /* Solve problem P */ while (P has not yet been solved) /* Solve subproblem P’ */. . . n Question: How can repeatedly doing P’ solve P ? n Answer: P’ must be parameterized in terms of some state. Each execution of P’ must change the state so that progress is made, i. e. , with each iteration, we move to a state that is “closer” to a solution for P. n The notion of “distance” must be well-founded, i. e. , it must converge to 0 in a finite number of steps that get “closer”. n Different notions of “distance” lead to different programs. CS 100 Lecture 5 12

Iterative Refinement, cont. n Example: Running a maze /* There are n 2 rooms arranged in an n-by-n grid. Some adjacent rooms have connecting doors. No doors lead outside. You are in the upper-leftmost room facing left. A sequence of doors leads to the lowerrightmost room. Get there. */ n Rule of thumb: Work some test cases by hand. Inspiration: Keep your left hand on the wall and keep walking (the left-hand rule). CS 100 Lecture 5 13

Iterative Refinement, cont. /* There are n 2 rooms arranged in an n-by-n grid. Some adjacent rooms have connecting doors. No doors lead outside. You are in the upperleftmost room facing left. A sequence of doors leads to the lower-rightmost room. Get there. */ while ( you are not in lower rightmost room ) /* Get “closer” to lower rightmost room. */. . . n Different notions of “closer” lead to different versions of /* Get “closer” to lower rightmost room. */. . . Notion A: wall length away, using the “left-hand rule”. Notion B: # of rooms away, using the “left-hand rule”. CS 100 Lecture 5 14

Iterative Refinement, cont. n Refinement A (using wall-length distance) /* There are n 2 rooms arranged in an n-by-n grid. Some adjacent rooms have connecting doors. No doors lead outside. You are in the upperleftmost room facing left. A sequence of doors leads to the lower-rightmost room. Get there. */ while ( you are not in lower rightmost room ) /* Get at least one wall “closer” to the lower rightmost room. */ if (you are facing a door){ Go through the door; Turn 90 degrees counter-clockwise; } else Turn 90 degrees clockwise; CS 100 Lecture 5 15

Iterative Refinement, cont. n Refinement B (using #rooms distance) /* There are n 2 rooms arranged in an n-by-n grid. Some adjacent rooms have connecting doors. No doors lead outside. You are in the upperleftmost room facing left. A sequence of doors leads to the lower-rightmost room. Get there. */ while ( you are not in lower rightmost room ) { /* Get at least one room “closer” to the lower rightmost room. */ while (you are not facing a door) Turn 90 degrees clockwise; Go through door; Turn 90 degrees counter-clockwise; } CS 100 Lecture 5 16