CS 100 J Lecture 16 n Previous Lecture

CS 100 J Lecture 16 n Previous Lecture – Programming concepts n Binary search n Application of the “rules of thumb” n Asymptotic complexity – Java Constructs n n Conditional Expressions This Lecture – Programming concepts n n CS 100 Alternative rules of thumb useful when you don’t know an algorithm Discovering an non-obvious algorithm by inventing a suitable loop invariant Lecture 16 1

Three-Way Partitioning of an Array n Problem. Characterize the values in an array as “red”, “white”, or “blue”, and sort the array into reds, then whites, then blues. n Rule of Thumb. Write a precise specification. /* Given array A[0. . N] consisting of “red” “white” and “blue” values in an arbitrary order, permute the values so that all reds precede all white, which precede all blues. */ static void sort(int[] A, int N) {. . . } CS 100 Lecture 16 2

Alternative Approach n Disregard the following rules of thumb: – Find inspiration from experience. – Work sample data by hand. Be introspective. Ask yourself: “What am I doing? ” n Instead, use the following rules of thumb: – Do not seek inspiration from experience. – Write down an example to clarify the problem requirements, but ignore how you get the answer. n Let negative numbers be “red”, 0 be “white”, and positive numbers be “blue”. Sample input: A 0 +1 1 -1 2 0 3 +3 4 -4 5=N -2 Sample output (the order within a “color” is arbitrary) A CS 100 0 -2 1 -1 2 -4 3 0 Lecture 16 4 +3 5=N +1 3

Loop Pattern n Rule of Thumb. If you smell an iteration, write it down. n Disregard the following rule: – Decide between for (definite) and while (indefinite) n Instead, just use the while. /* Given array A[0. . N] consisting of “red” “white” and “blue” values in an arbitrary order, permute the values so that all reds precede all white, which precede all blues. */ static void sort(int[] A, int N) { . . . while ( ____________) {. . . } CS 100 Lecture 16 4

Characterize Initial and Final States n Disregard the following rule of thumb. – Characterize the state after an arbitrary number of iterations, either in English or in a diagram. n Instead: – Characterize the initial and final states. Initial: 0 N ? A Final: 0 A red white blue N and the final A is a permutation of the original A. CS 100 Lecture 16 5

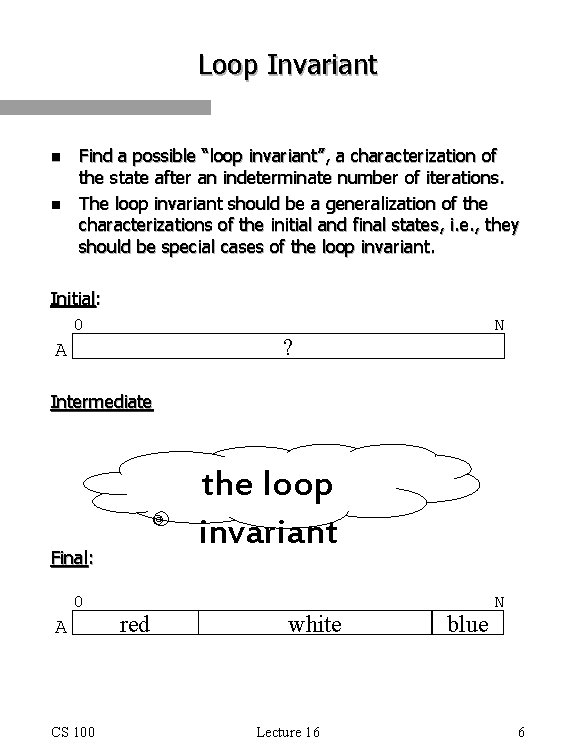
Loop Invariant n n Find a possible “loop invariant”, a characterization of the state after an indeterminate number of iterations. The loop invariant should be a generalization of the characterizations of the initial and final states, i. e. , they should be special cases of the loop invariant. Initial: 0 N ? A Intermediate the loop invariant Final: 0 A CS 100 red white Lecture 16 blue N 6

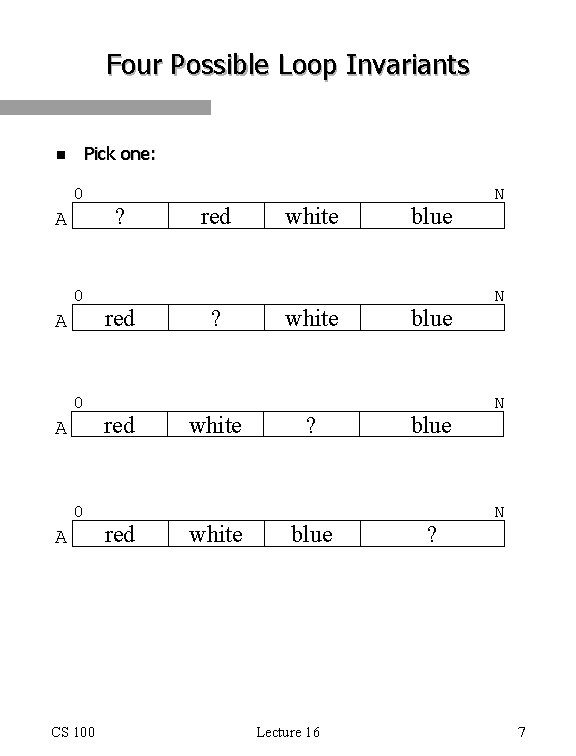
Four Possible Loop Invariants Pick one: n 0 A 0 A CS 100 ? red red ? white ? blue Lecture 16 blue ? N N 7

Identify boundaries with variables n n Introduce a variable to record the subscript of each boundary expected to change independently during the iteration. Indicate the position of each variable in each of the three characterizations. W Q 0 ? A 0 A CS 100 NB red W white W Q ? white Lecture 16 B blue Q B blue N N 8

Identify boundaries with variables n n Introduce a variable to record the subscript of each boundary expected to change independently during the iteration. Indicate the position of each variable in each of the three characterizations. 0 ? A 0 A CS 100 N red white ? white Lecture 16 blue N N 9

Initialization and Termination n Rule of Thumb – Use the characterizations to refine the initialization and termination condition of the loop. /* Given array A[0. . N] consisting of “red” “white” and “blue” values in an arbitrary order, permute the values so that all reds precede all white, which precede all blues. */ static void sort(int[] A, int N) { W = 0; Q = 0; B = N + 1; while ( Q != B ) {. . . } CS 100 Lecture 16 10

Specify the Body n Rule of Thumb. – Use the characterization to specify what the loop body must accomplish. /* Given array A[0. . N] consisting of “red” “white” and “blue” values in an arbitrary order, permute the values so that all reds precede all white, which precede all blues. */ static void sort(int[] A, int N) { W = 0; Q = 0; B = N + 1; while ( Q != B ) { // Reduce the size of the ? region // while maintaining the invariant. . } } CS 100 Lecture 16 11

Refine the Body // Reduce the size of the ? region // while maintaining the invariant. n Case analysis on A[Q] 0 A red W white Q ? B blue N A[Q] is white: Q++; A[Q] is blue: swap A[Q] with A[B-1]; B--; A[Q] is red: swap A[Q] with A[W]; W++; Q++; CS 100 Lecture 16 12

Code the body /* Given array A[0. . N] consisting of “red” “white” and “blue” values in an arbitrary order, permute the values so that all reds precede all white, which precede all blues. */ static void sort(int[] A, int N) { W = 0; Q = 0; B = N + 1; while ( Q != B ) { // Reduce the size of the ? Region // while maintaining the invariant. if ( A[Q] is red ) { // swap A[Q] with A[W]. int temp = A[Q]; A[Q] = A[W]; A[W] = temp ; W++; Q++; } else if ( A[Q] is white ) Q++; else // A[Q] is blue. { // swap A[Q] with A[B-1]. int temp = A[Q]; A[Q] = A[B-1]; A[B-1] = temp ; B--; } } } CS 100 Lecture 16 13

Final Program /* Given array A consisting of integers in an arbitrary order, permute the values so that all negatives precede all zeros, which precede all positives. */ static void sort(int[] A) { int N = A. length – 1; W = 0; Q = 0; B = N + 1; while ( Q != B ) { // Reduce the size of the ? Region // while maintaining the invariant. if ( A[Q] < 0 ) { // swap A[Q] with A[W]. int temp = A[Q]; A[Q] = A[W]; A[W] = temp ; W++; Q++; } else if ( A[Q] == 0 ) Q++; else // A[Q] is positive. { // swap A[Q] with A[B-1]. int temp = A[Q]; A[Q] = A[B-1]; A[B-1] = temp ; B--; } } } CS 100 Lecture 16 14

Check Boundary Conditions n What happens on the first and last iterations? W Q 0 NB 0 N ? A A red W white QB ? blue A[Q] is white: Q++; A[Q] is blue: swap A[Q] with A[B-1]; B--; A[Q] is red: swap A[Q] with A[W]; W++; Q++; CS 100 Lecture 16 15

Termination n The loop will terminate is there is an integer notion of “distance”, i. e. , a formula, that is: – necessarily non-negative, and – guaranteed to be reduced by at least 1 on each iteration. n Q. What is that notion of distance? n A. The size of the ? region, i. e. , max(0, B-Q). n Check. In each of the three cases, this is reduced by 1. CS 100 Lecture 16 16

Asymptotic Complexity n Because the size of the ? region is reduced by 1 on each iteration, the number of iterations is N+1. n Thus, because the time spent on each iteration is bounded by a constant number of steps, the total running time is linear in N. n In contrast, the total running time of the general sorting algorithm from Lecture 14 is quadratic in N. CS 100 Lecture 16 17