Crystal Vibration Crystal Vibration Interatomic Bonding Spring constant

Crystal Vibration
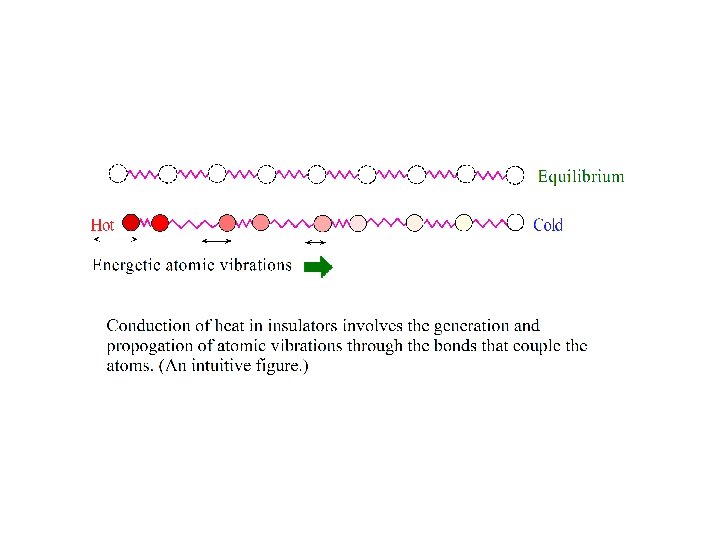
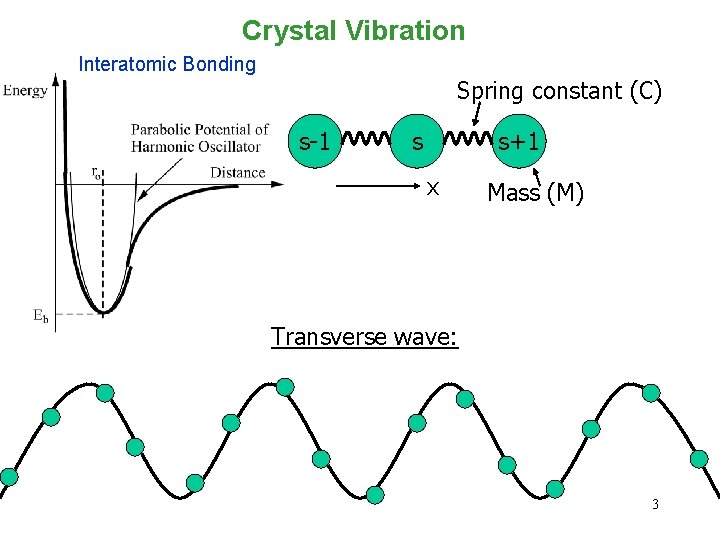
Crystal Vibration Interatomic Bonding Spring constant (C) s-1 s s+1 x Mass (M) Transverse wave: 3
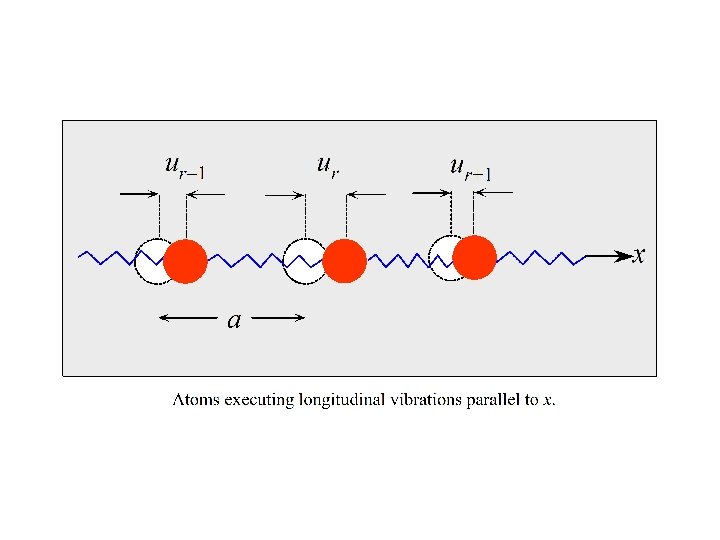
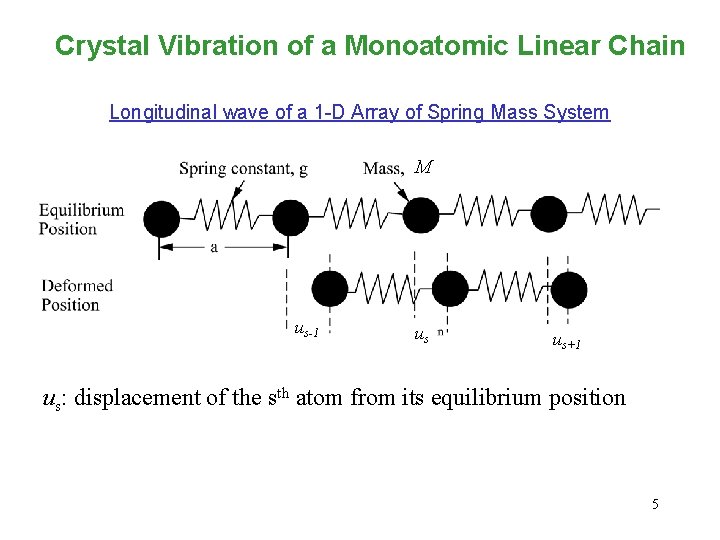
Crystal Vibration of a Monoatomic Linear Chain Longitudinal wave of a 1 -D Array of Spring Mass System M us-1 us us+1 us: displacement of the sth atom from its equilibrium position 5
6

Solution of Lattice Dynamics s-1 s s+1 Same M Wave solution: u(x, t) ~ uexp(-iwt+i. Kx) Time dep. : w: frequency K: wavelength = uexp(-iwt)exp(is. Ka)exp( i. Ka) cancel Identity: Trig: 7
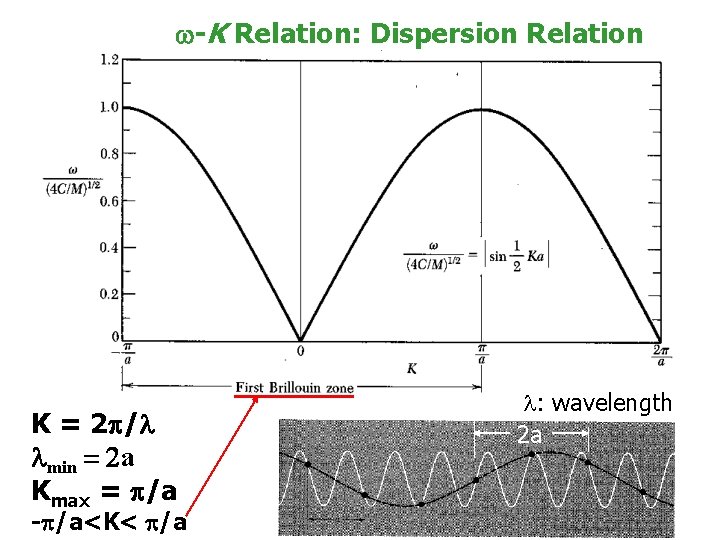
w-K Relation: Dispersion Relation K = 2 /l lmin = 2 a Kmax = /a - /a<K< /a l: wavelength 2 a 8
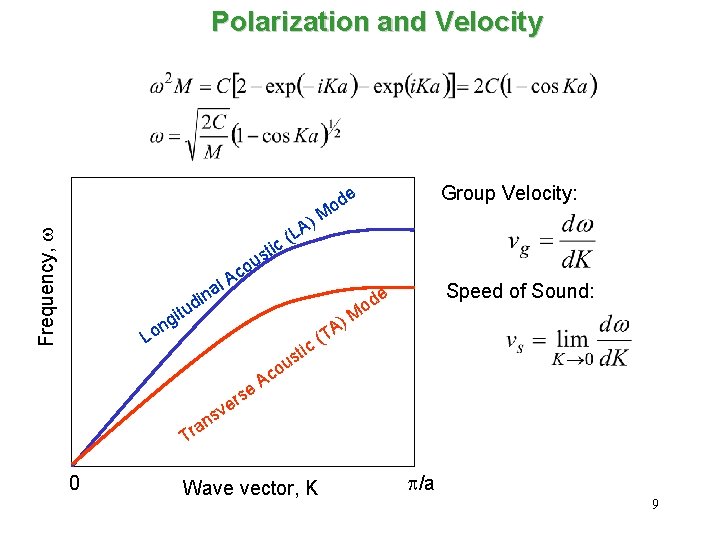
Polarization and Velocity Group Velocity: Frequency, w e ) A L c( d o M ti c A al i g on s ou in d u t L c sti ns a r se r ve ( ) TA Speed of Sound: e od M ou c A T 0 Wave vector, K p/a 9
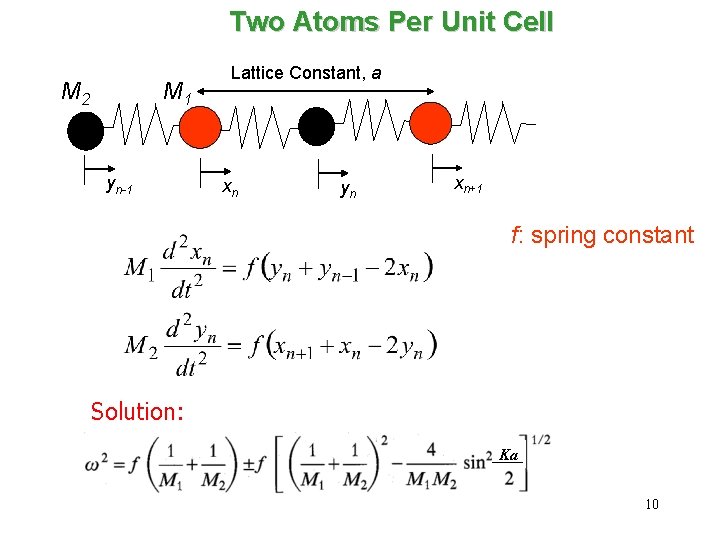
Two Atoms Per Unit Cell M 2 M 1 yn-1 Lattice Constant, a xn yn xn+1 f: spring constant Solution: Ka 10

Acoustic and Optical Branches Ka 1/µ = 1/M 1 + 1/M 2 What is the group velocity of the optical branch? What if M 1 = M 2 ? K 11
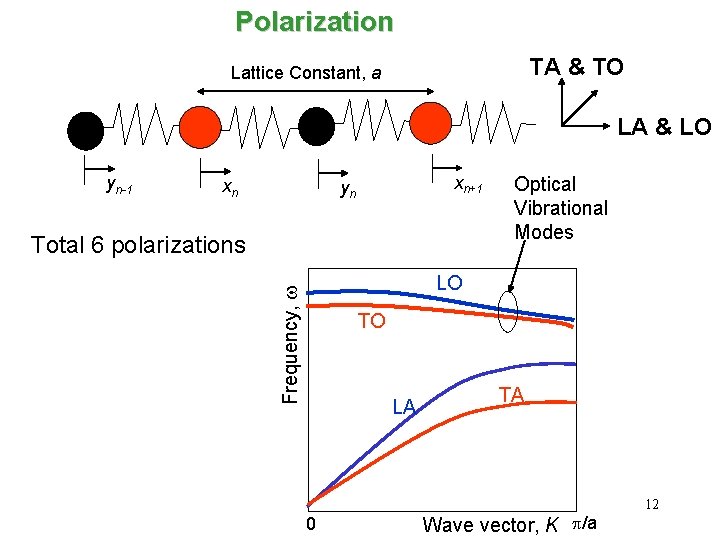
Polarization TA & TO Lattice Constant, a LA & LO yn-1 xn xn+1 yn Total 6 polarizations Optical Vibrational Modes Frequency, w LO TO LA 0 TA Wave vector, K p/a 12
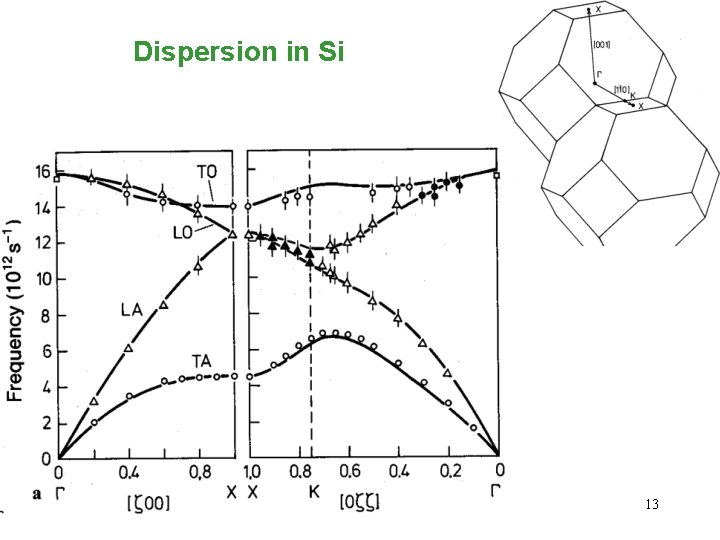
Dispersion in Si 13
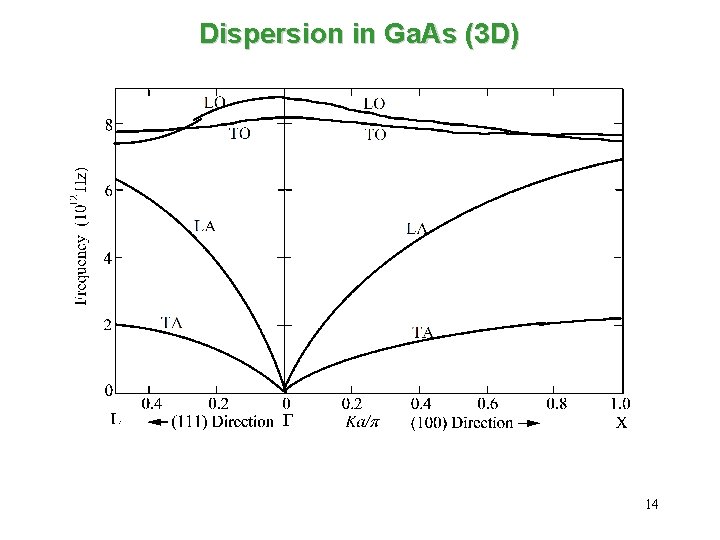
Dispersion in Ga. As (3 D) 14

Allowed Wavevectors (K) A linear chain of N=10 atoms with two ends jointed a Solution: us ~u. K(0)exp(-iwt)sin(Kx), x =sa B. C. : us=0 = us=N=10 x K= 2 np/(Na), n = 1, 2, …, N Na = L Only N wavevectors (K) are allowed (one per mobile atom): K= -8 p/L -6 p/L -4 p/L -2 p/L 0 2 p/L 4 p/L 6 p/L 8 p/L p/a=Np/L 15
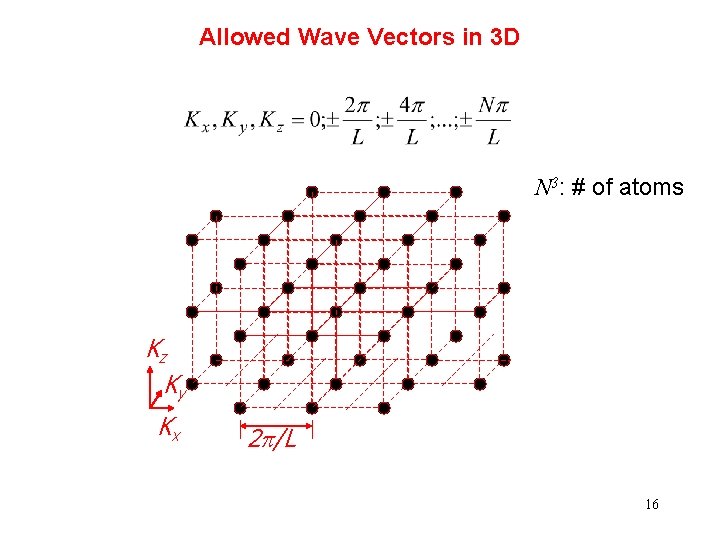
Allowed Wave Vectors in 3 D N 3: # of atoms Kz Ky Kx 2 p/L 16

Phonon • The linear atom chain can only have N discrete K w is also discrete • The energy of a lattice vibration mode at frequency w was found to be • where ħw can be thought as the energy of a particle called phonon, as an analogue to photon • n can be thought as the total number of phonons with a frequency w, and follows the Bose-Einstein statistics: Equilibrium distribution 17

Total Energy of Lattice Vibration p: polarization(LA, TA, LO, TO) K: wave vector 18
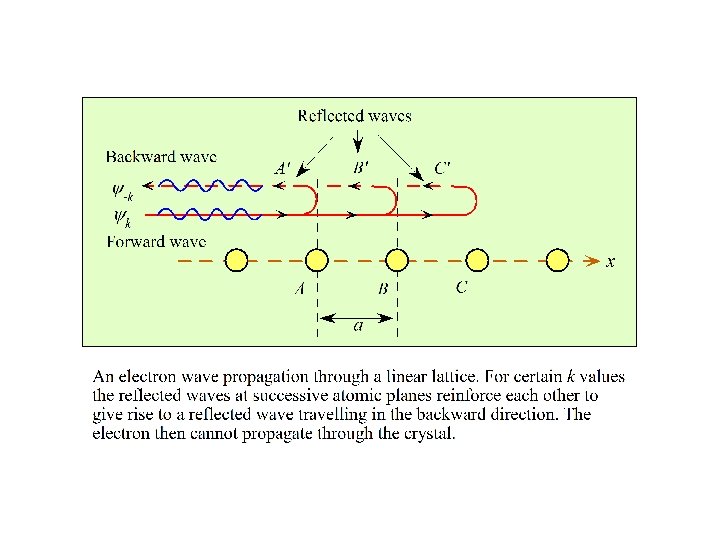
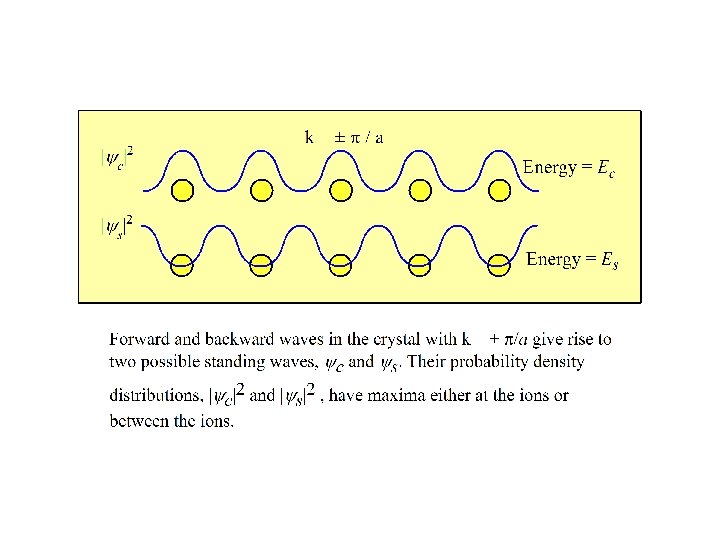
- Slides: 20