Crystal Structure and Crystallography of Materials Chapter 12

Crystal Structure and Crystallography of Materials Chapter 12: Space Group #3 (Space Groups containing operations of the 2 nd sort: containing mirror plane and inversion center )

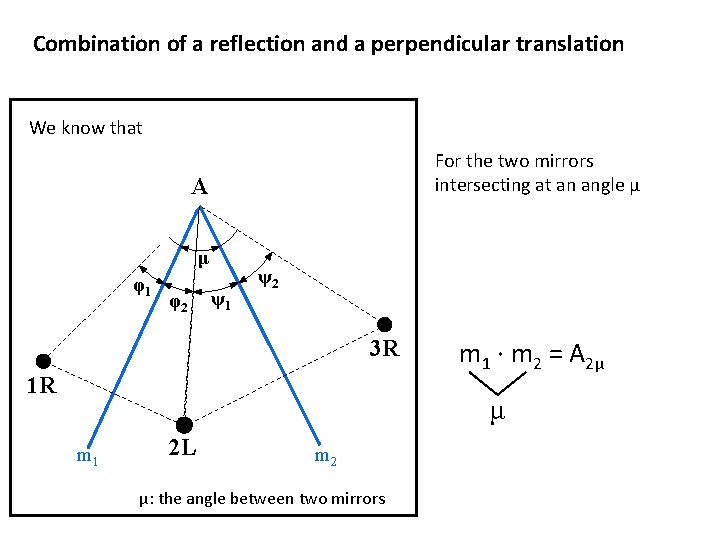
Combination of a reflection and a perpendicular translation We know that For the two mirrors intersecting at an angle μ A μ φ1 φ2 ψ1 ψ2 3 R 1 R m 1 · m 2 = A 2μ μ m 1 2 L m 2 μ: the angle between two mirrors

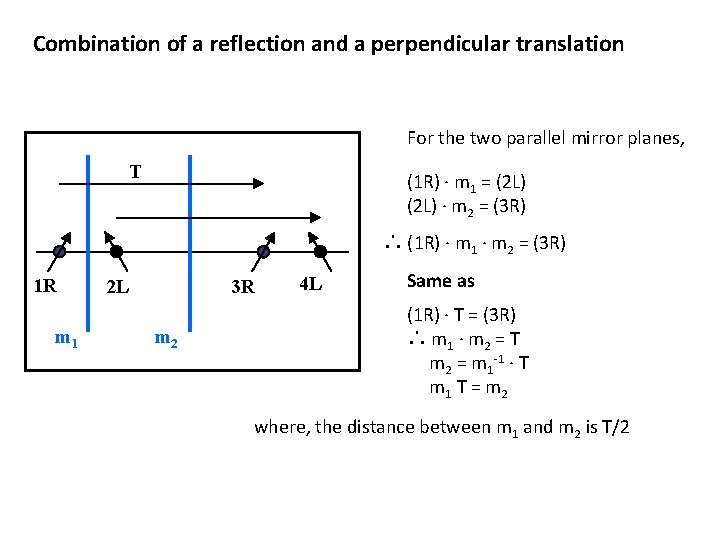
Combination of a reflection and a perpendicular translation For the two parallel mirror planes, T (1 R) · m 1 = (2 L) · m 2 = (3 R) ∴ (1 R) · m 1 · m 2 = (3 R) 1 R m 1 2 L 3 R m 2 4 L Same as (1 R) · T = (3 R) ∴ m 1 · m 2 = T m 2 = m 1 -1 · T m 1 T = m 2 where, the distance between m 1 and m 2 is T/2

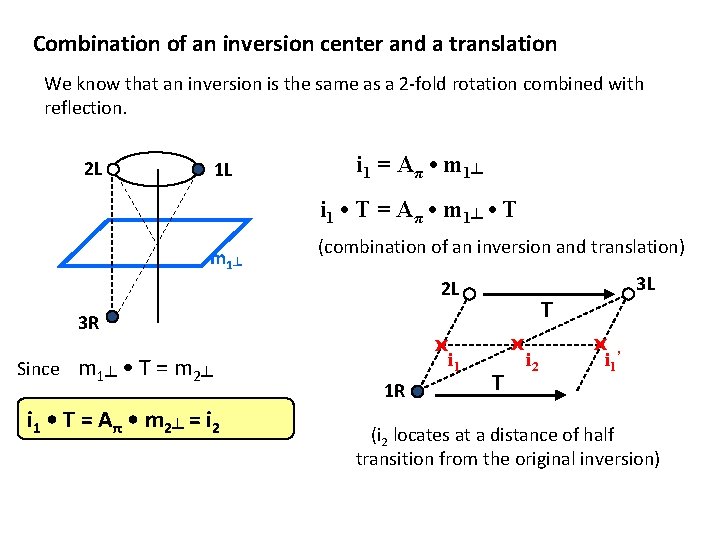
Combination of an inversion center and a translation We know that an inversion is the same as a 2 -fold rotation combined with reflection. 2 L 1 L i 1 = Aπ • m 1┴ i 1 • T = Aπ • m 1┴ • T m 1┴ (combination of an inversion and translation) 2 L 3 R Since m 1┴ • T = m 2┴ i 1 • T = Aπ • m 2┴ = i 2 x i 1 1 R 3 L T x T i 2 x ’ i 1 (i 2 locates at a distance of half transition from the original inversion)

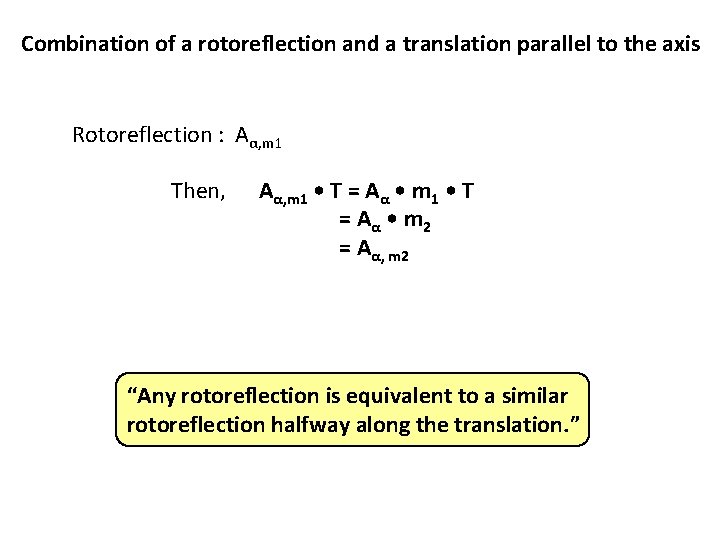
Combination of a rotoreflection and a translation parallel to the axis Rotoreflection : Aα, m 1 Then, Aα, m 1 • T = Aα • m 1 • T = A α • m 2 = Aα, m 2 “Any rotoreflection is equivalent to a similar rotoreflection halfway along the translation. ”

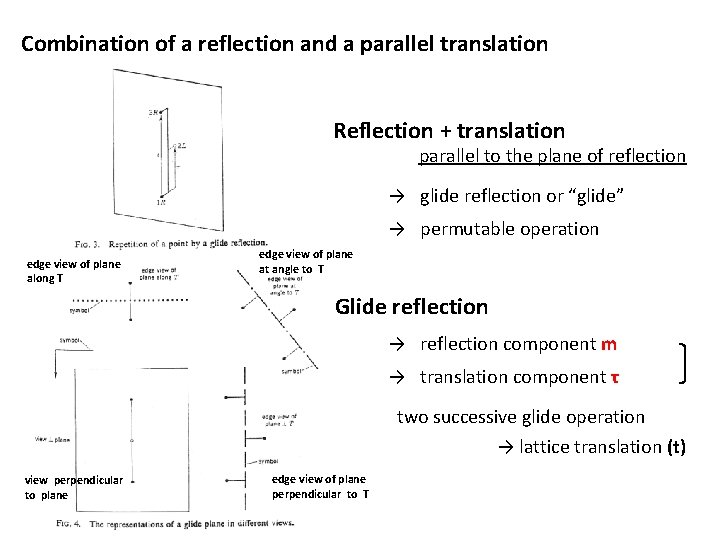
Combination of a reflection and a parallel translation Reflection + translation parallel to the plane of reflection → glide reflection or “glide” → permutable operation edge view of plane along T edge view of plane at angle to T Glide reflection → reflection component m → translation component τ two successive glide operation → lattice translation (t) view perpendicular to plane edge view of plane perpendicular to T

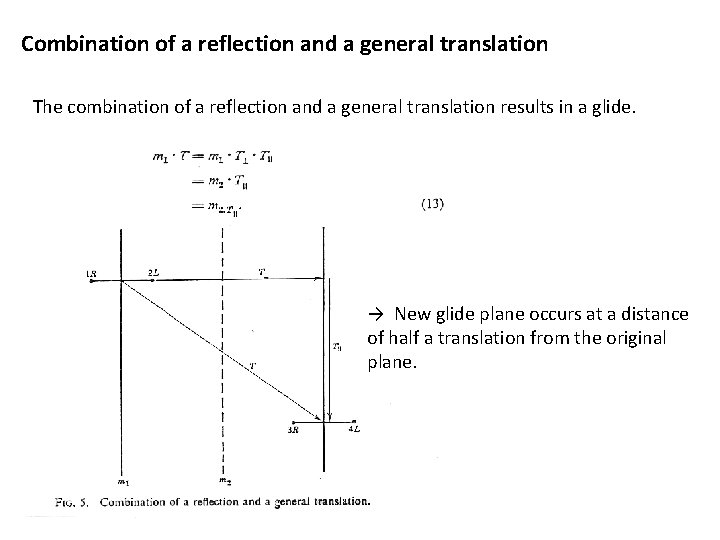
Combination of a reflection and a general translation The combination of a reflection and a general translation results in a glide. → New glide plane occurs at a distance of half a translation from the original plane.

Combination of a reflection and a general translation Wherever the point group of a crystal has a reflection plane, the space group may have sets of parallel reflection plane, glide planes, or both. → glide planes are isogonal with reflection planes. Again, ► glide plane in space-group → reflection plane among point-group ► screw axis in space-group → rotation axis among point-group

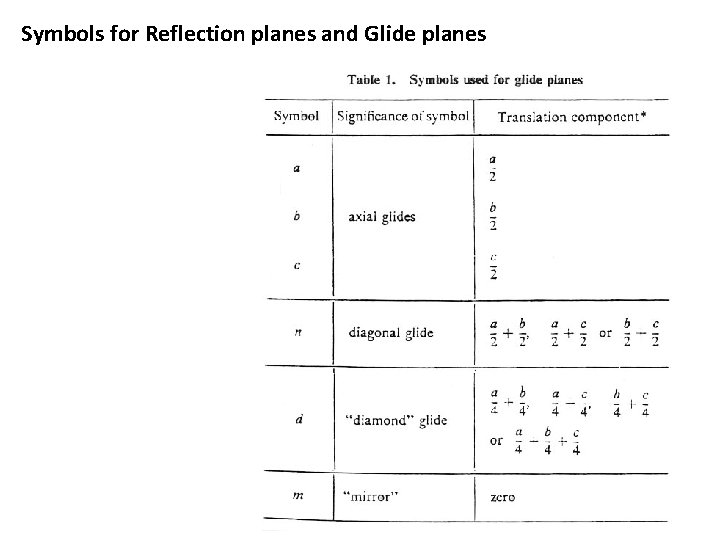
Symbols for Reflection planes and Glide planes

Combination of a Glide Plane and a General Translation: When the component of the translation parallel to the glide plane be different from the translation component τ of the glide. m 1, τ · T = m 1 · τ · T 11 · T┴ = m 1 T┴ · τ · T 11 = m 2, τ+T 11 A glide plane at a perpendicular distance of half a translation from the original glide plane, and having translation components τ+T 11.

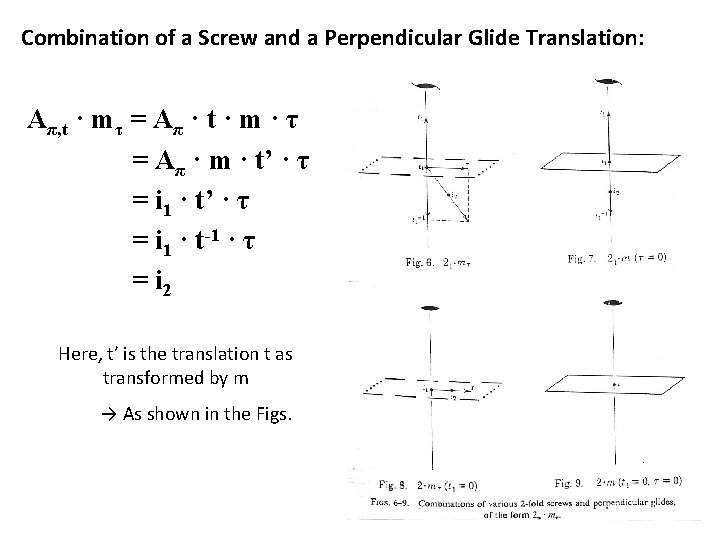
Combination of a Screw and a Perpendicular Glide Translation: Aπ, t · mτ = Aπ · t · m · τ = Aπ · m · t’ · τ = i 1 · t-1 · τ = i 2 Here, t’ is the translation t as transformed by m → As shown in the Figs.

Triclinic Space Group: Point group 1 : The only operation isogonal with an inversion is an inversion. P 1 1. inversion center at origin 2. i 1 · T = i 2 where T: a, b, c, a+b, b+c, a+b+c.

Monoclinic Space Group: Point group m : the symmetry elements isogonal with this reflection plane are a reflection plane m and a glide plane mτ. → combine these with the permissible lattices (P and I) Two settings in the monoclinic system A) symmetry plane parallel to (001) B) symmetry plane parallel to (010)

Monoclinic Space Group: Pm: Pa: If a glide is combined with the translations of P, the translation component of the glide must be half of a cell translation parallel to the plane, → Pa, Pb, Pn → regarded as one space group → the choice of cell edge is different (only).

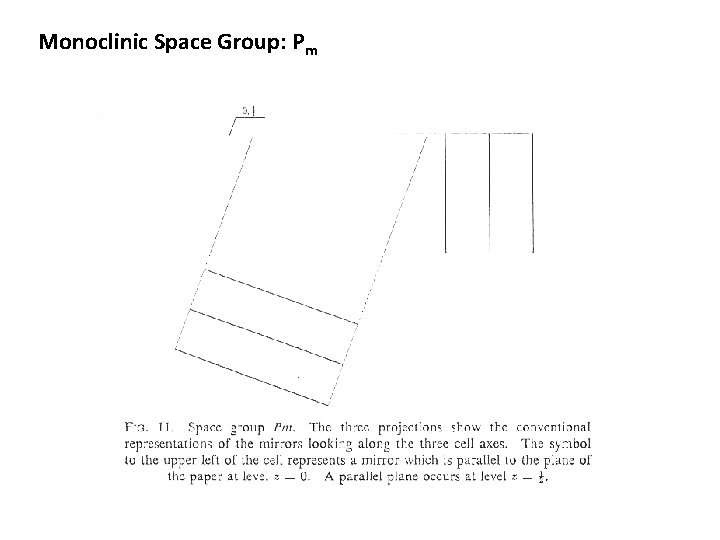
Monoclinic Space Group: Pm

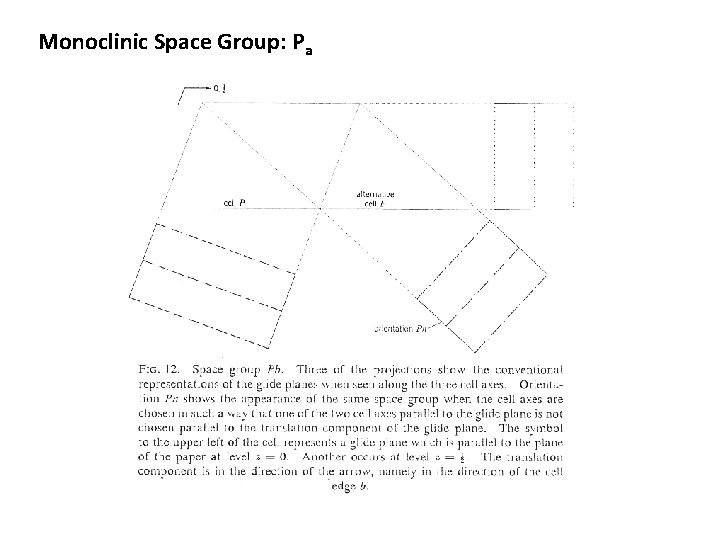
Monoclinic Space Group: Pa

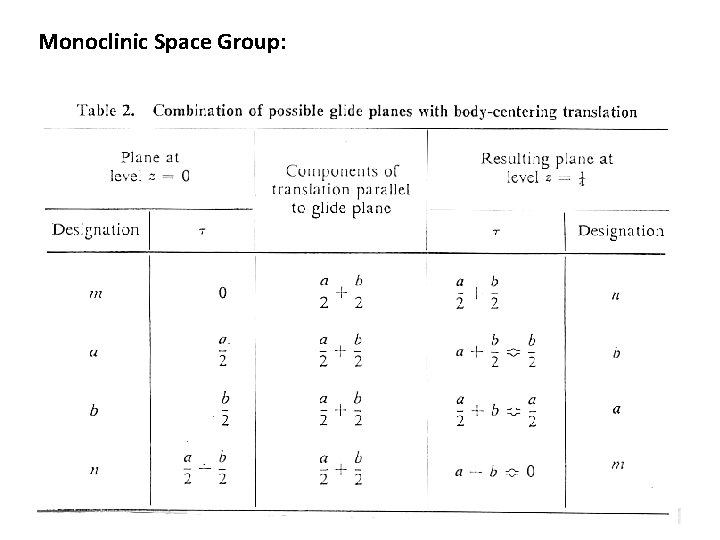
Monoclinic Space Group: Consider combining mτ with the translations of I. Same translations as P, plus the additional translation Space group Im and Ib contains the symmetry elements of Pm and Pb and have, in addition, symmetry elements due to the combination of Produce a glide at c/4 and 3 c/4. since, mτT 11 = mτ+a/2+b/2

Monoclinic Space Group:

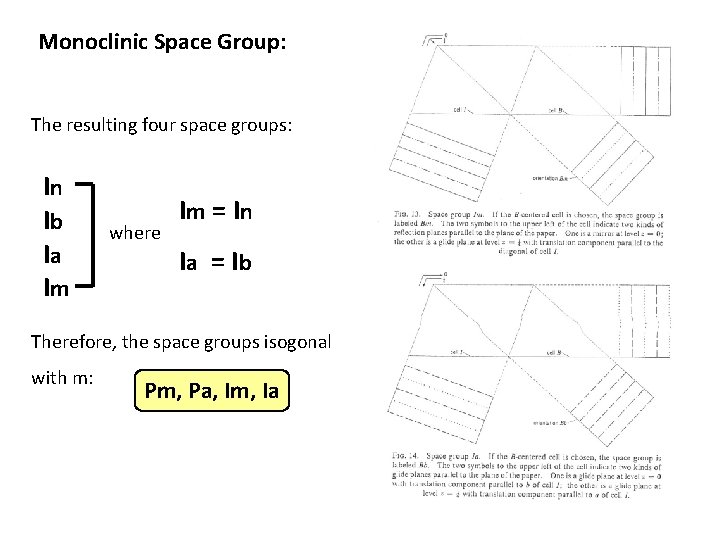
Monoclinic Space Group: The resulting four space groups: In Ib Ia Im where Im = I n Ia = Ib Therefore, the space groups isogonal with m: Pm, Pa, Im, Ia

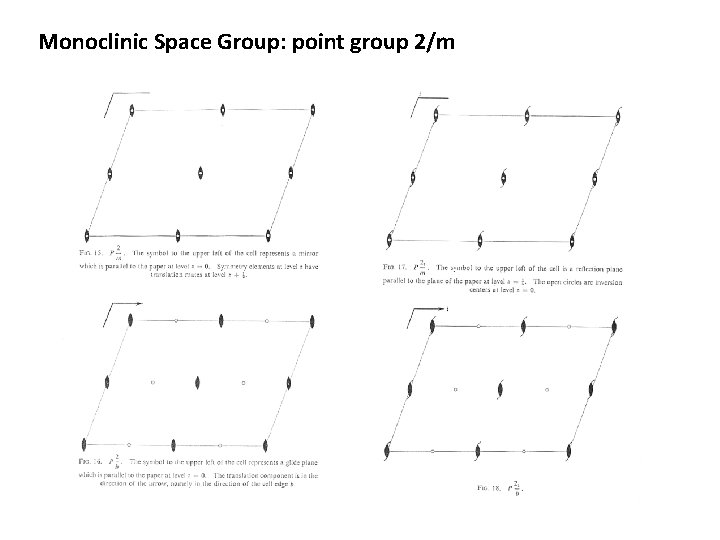
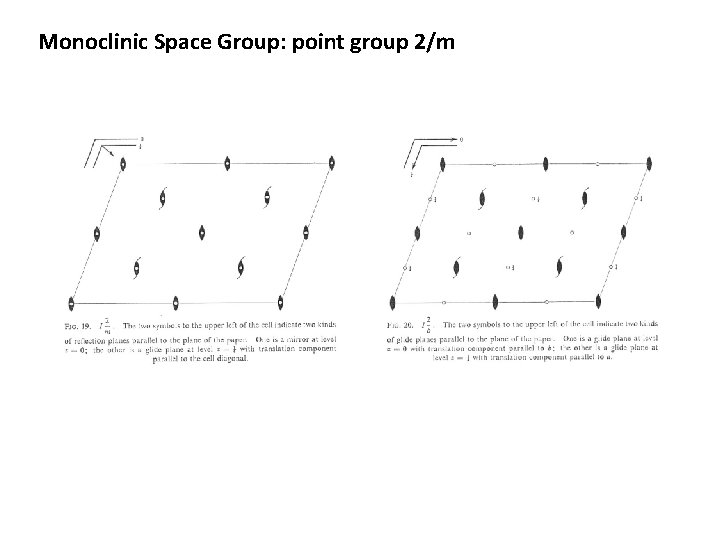
Monoclinic Space Group: point group 2/m contains three symmetry elements, 2, m, and i. → the space groups isogonal with this point groups isogonal with any two of the point groups 2, m, or 1. Six space group results: i 1 : inversion to be added on an axis. i 2 : inversion to be added halfway between axis.

Monoclinic Space Group: point group 2/m

Monoclinic Space Group: point group 2/m

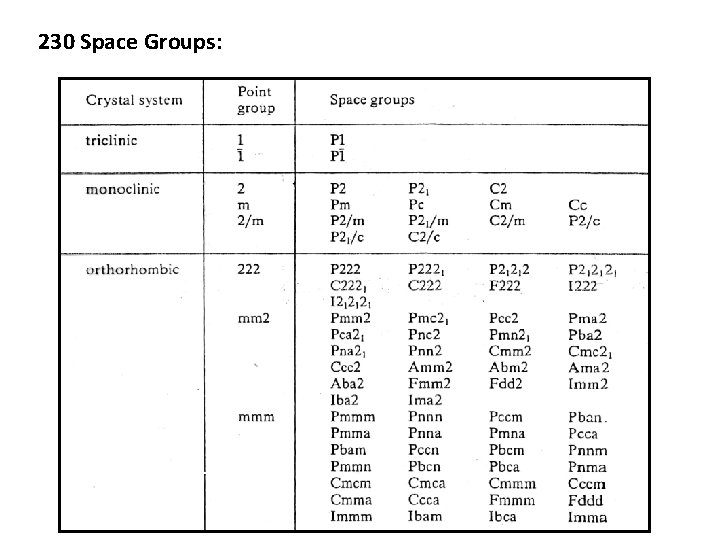
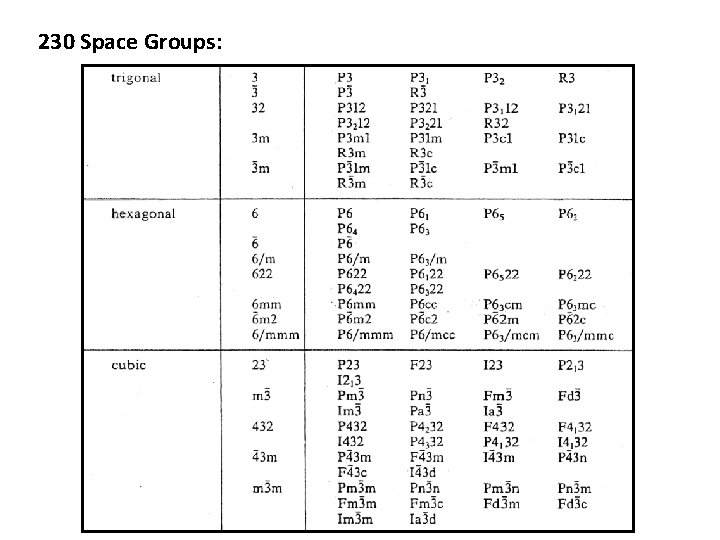
230 Space Groups:

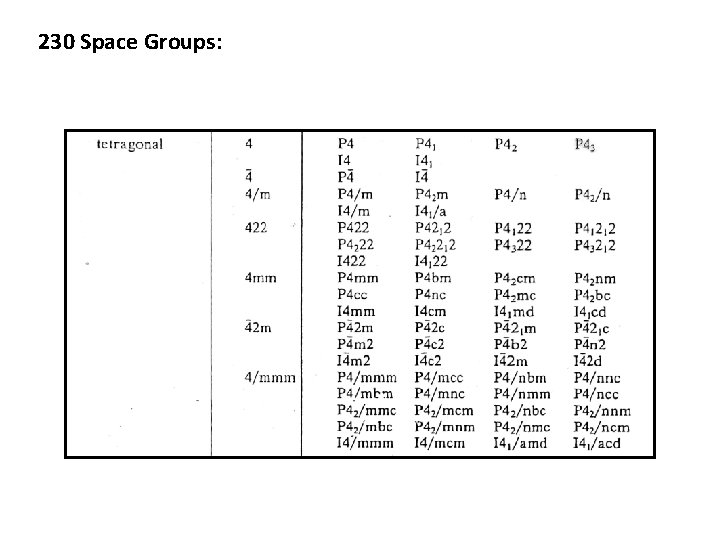
230 Space Groups:

230 Space Groups:

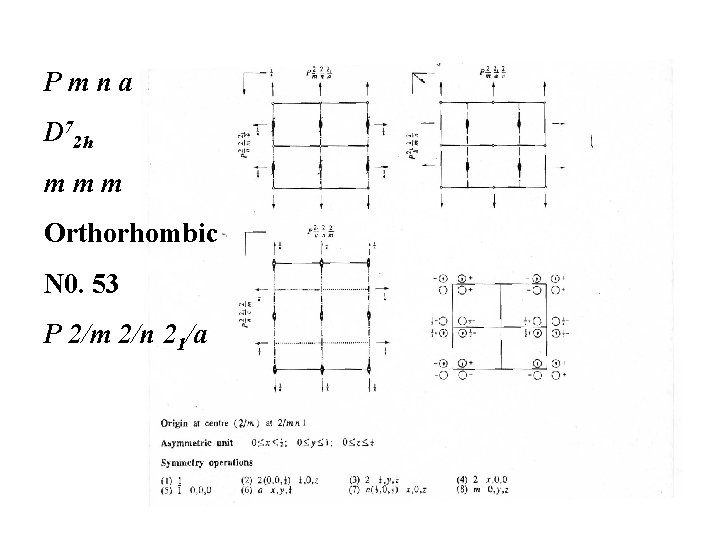
Pmna D 72 h mmm Orthorhombic N 0. 53 P 2/m 2/n 21/a

continued Pmna N 0. 53

P 42/m n m D 144 h 4/m m m Tetragonal N 0. 136 P 42/m 21/n 2/m