Cryptosystems Based on Discrete Logarithms 1 Outline 1

Cryptosystems Based on Discrete Logarithms 1

Outline • [1] Discrete Logarithm Problem • [2] Algorithms for Discrete Logarithm – – – A trivial algorithm Shanks’ algorithm (Baby-step Giant-step) Pollard’s algorithm Pohlig-Hellman algorithm Adleman’s algorithm (the index calculus method) • [3] Cryptosystems Based on Discrete Logarithm – Key distribution – Encryption – Digital signature 2

[1] Discrete Logarithm Problem • Let G be a finite multiplicative group (G, *). For an element α G having order n, define. <α> = {α i | i = 0, 1, 2, …, n-1} Then <α> is a subgroup of G, and <α> is cyclic of order n. • Discrete logarithm problem 3

Discrete Logarithm Problem • Example 1 G = Z*19 = { 1, 2, …, 18} n=18, generator g = 2 then log 214 = 7 log 26 = 14 4

Discrete Logarithm Problem • Example 2 In Z*11 = { 1, 2, …, 10} Let G= <3> ={1, 3, 9, 5, 4}, n=5, 3 is not a generator of Z*11 but a generator of G. log 35 = 3 5

Discrete Logarithm Problem • Example 3 G=GF*(23) with irreducible poly. p(x) = x 3 + x +1 G=Zp*/p(x) = { 1, x, x 2, 1+x 2, x+x 2, 1+x+x 2 } n=7, generator g = x then logx(x+1) = 3 logx(x 2+x+1) = 5 logx(x 2+1) = 6 6

Discrete Logarithm Problem • Example 4 Let p =105354628039501697530461658293395873194887 18149259134893426087342587178835751858673003 86287737705577937382925873762451990450430661 35085968269741025626827114728303489756321430 02371663691740666159071764725494700831131071 38189921280884003892629359 NB: p = 158(2800 + 25) + 1 and has 807 bits. • Find such that 7

[2] Algorithms for Discrete Logarithm • • • A trivial algorithm Shanks’ algorithm (Baby-step giant-step) Pollard rho discrete log algorithm Pohlig-Hellman algorithm The index calculus method 8

A trivial algorithm • Discrete Logarithm Problem in Zp* given generator α (i. e. <α>= Zp*) and β in Zp* , find a in Zp-1={0, 1, …, p-2} s. t. β = αa mod p • A trivial algorithm – Compute αi and test if β = αi – Time complexity O(p) 9

Shanks’ algorithm • Shanks’ algorithm (Baby-step giant-step) (1972) – Compute L 1 = {(i, αmi), i = 0, 1, …, m-1} L 2 = {(i, βα-i), i = 0, 1, …, m-1} – where m = ceiling((p-1) ½) Sort L 1 and L 2 with respect to the 2 nd coordinate. – Find the same 2 nd coordinate from L 1 and L 2, say, (q, αmq), (r, βα-r), to get αmq =βα-r. So β = αmq + r and a = mq+r. – Time complexity O(m log m) = O(p 1/2 log p) – Space complexity O(p 1/2) 10

Example 1 log 215 mod 19 =? G = Z*19 = { 1, 2, …, 18} α = 2, α-1 = 10, n = p-1 = 18, m = 5, αm = 13 β = 15 L 1: (i, αmi) (0, 1) (1, 13) (2, 17) (3, 12) (4, 4) L 2: (i, βα-i) (0, 15) (1, 17) (2, 18) (3, 9) (4, 14) log 215 mod 19 = 11 q=2 r=1 mq + r = 11 11

Example 2 log 3525 mod 809 =? G = Z*809 = { 1, 2, …, 808} = <3> α = 3, α-1 = 10, n = p-1 = 808, m = 29, αm = 99 β = 525 L 1: (i, αmi) (0, 1) (1, 99) (2, 93) (3, 308) (4, 559) (5, 329) (6, 211) (7, 664) (8, 207) (9, 268) (10, 644) (11, 654) (12, 26) L 2: (i, βα-i) (0, 525) (1, 175) (2, 328) (3, 379) (4, 396) (5, 132) (6, 44) (7, 554) (8, 724) (9, 511) (10, 440) (11, 686) (12, 768) 12

L 1: (i, αmi) (13, 147) (14, 800) (15, 727) (16, 781) (17, 464) (18, 632) (19, 275) (20, 528) (21, 496) (22, 564) (23, 15) (24, 676) (25, 586) (26, 575) (27, 295) (28, 81) L 2: (i, βα-i) (13, 256) (14, 355) (15, 388) (16, 399) (17, 133) (18, 314) (19, 644) (20, 754) (21, 521) (22, 713) (23, 777) (24, 259) (25, 356) (26, 658) (27, 489) (28, 163) q = 10, r = 19, so mq + r = 29*10+19 mod 808 = 309 and log 3525 mod 809 = 309 13

Pollard rho DL algorithm • Pollard rho discrete logarithm algorithm (1978) compute integers s and t such that – partition the group G into three roughly equal-sized set S 1 , S 2 and S 3. Let x 0 = 1 G and x 0 is not in S 2 14

where n = p-1 when G = Z*p 15

We should expect some integer , then this gives with If then compute and we have , so that If little work to do. . . (Omitted) such that 16

• Floyd’s cycle-finding algorithm: One starts with the pair (x 1, x 2), and iteratively computes (xi, x 2 i) from the previous (xi-1, x 2 i-2), until xm=x 2 m for some m. The expected running time of this method is O(n 1/2). 17

• Pollard’s rho algorithm for discrete logarithms – INPUT: a generator α of a cyclic group G of prime order n, and β is an element of G – OUTPUT: 1. Set x 0 1, a 0 0, b 0 0 2. For i = 1, 2, …. Do the following: 2. 1 Use xi-1, ai-1, bi-1 to compute xi, ai, bi Use x 2 i-2, a 2 i-2, b 2 i-2 to compute x 2 i, a 2 i, b 2 i 2. 2 if xi=x 2 i, then do the following set r bi – b 2 i if gcd(r, n) ≠ 1 then return ‘failure’ else return r-1(a 2 i-ai) mod n 18

• Example: α= 2 is a generator of the subgroup G of Z 383* of order n= 191. (in this case <α> = G ≠ Z 383* ) Suppose β = 228. Find log 2228. Solution: Partition G into 3 subsets, let 19

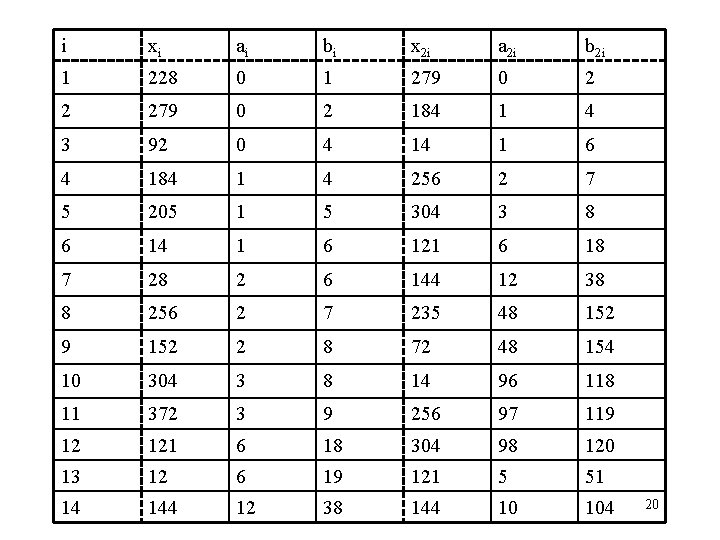
i xi ai bi x 2 i a 2 i b 2 i 1 228 0 1 279 0 2 2 279 0 2 184 1 4 3 92 0 4 14 1 6 4 184 1 4 256 2 7 5 205 1 5 304 3 8 6 14 1 6 121 6 18 7 28 2 6 144 12 38 8 256 2 7 235 48 152 9 152 2 8 72 48 154 10 304 3 8 14 96 118 11 372 3 9 256 97 119 12 121 6 18 304 98 120 13 12 6 19 121 5 51 14 144 12 38 144 10 104 20

• Solution (continued): From the table, we have x 14 = x 28 = 144. Finally compute r = a 14 -a 28 mod 191=125 r-1 = 125 -1 mod 191 = 136, and r-1(b 28 - b 14) mod 191 = 110. Hence, log 2228 = 110. 21

Pohlig-Hellman algorithm • Pohlig-Hellman algorithm (1978) If <α> is of order n and β in <α> then a = logαβ is determined (uniquely) mod n. Eg. If <α> = Zp* (i. e. α is a generator of Zp*), then n = p-1 Let The idea of Pohlig-Hellman algorithm is that we can compute a mod pici for each i, then we compute a mod n by CRT (Chinese remainder theorem). (see Text for details) 22

The index calculus method • The index calculus method (Suitable only for G=Zp*) 23

• Example log 59451 mod 10007=? Choose B={2, 3, 5, 7}. Of course log 55=1. Use lucky exponents 4063, 5136, and 9865 54063 mod 10007 = 42 = 2 * 3 * 7 55136 mod 10007 = 54 = 2 * 33 59865 mod 10007 = 189 = 33 * 7 And we have three congruences: log 52 + log 53 + log 57 = 4063 mod 10006 log 52 + 3 log 53 = 5136 mod 10006 3 log 53 + log 57 = 9865 mod 10006 24

There happens to be a unique solution modulo 10006 log 52=6578, log 53=6190, and log 57=1301 Choose random exponent s = 7736 and try to calculate βαs = 9451*57736 mod 10007 = 8400 Since 8400 = 24*3*52*7 factors over B, we obtain log 59451 = (4 log 52 + log 53 + 2 log 55 + log 57 – s) mod 10006 = (4*6578 + 6190 + 2*1 +1301 – 7736) mod 10006 = 6057 mod 10006 25

[3] Cryptosystems based on DL • Key Distribution – Diffie-Hellman, 1976 • Encryption – Massey-Omura cryptosystem, 1983 • Digital Signature – El. Gamal, 1985 26

Diffie-Hellman Key Exchange Algorithm • Global Public Elements – q : prime number – α: α< q and α is a primitive root of q • User A Key Generation – Select private XA : XA< q – Calculate public YA : YA= αXA mod q • User B Key Generation – Select private XB : XB< q – Calculate public YB : YB= αXB mod q • Generation of Secret Key by User A – K = (YB)XA mod q • Generation of Secret Key by User B – K = (YA)XB mod q 27

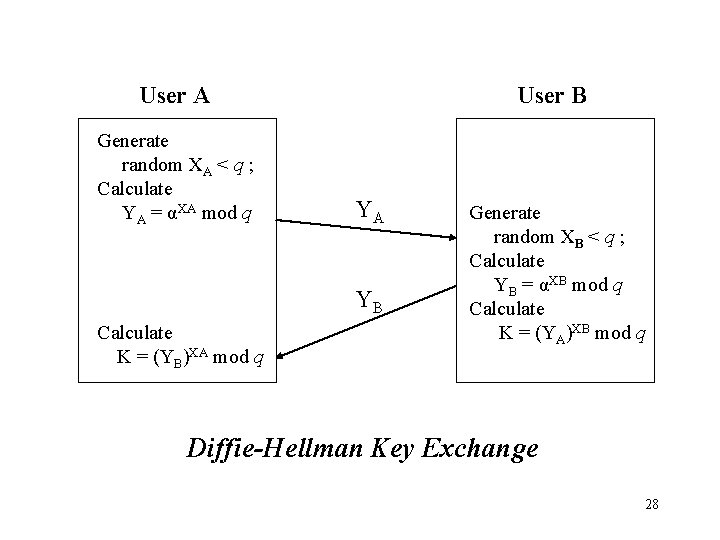
User A Generate random XA < q ; Calculate YA = αXA mod q User B YA YB Calculate K = (YB)XA mod q Generate random XB < q ; Calculate YB = αXB mod q Calculate K = (YA)XB mod q Diffie-Hellman Key Exchange 28

Massey-Omura for message transmission • Parameters – q : prime number – e : a random private integer • 0 < e < q and gcd ( e, q-1) = 1 – d : an inverse of e • d = e-1 mod q-1 , i. e. , de≡ 1 mod q-1 – M : a message to be encrypted and decrypted • User A wants to send a message M to User B – User A : e. A and d. A are both private – User B : e. B and d. B are both private 29

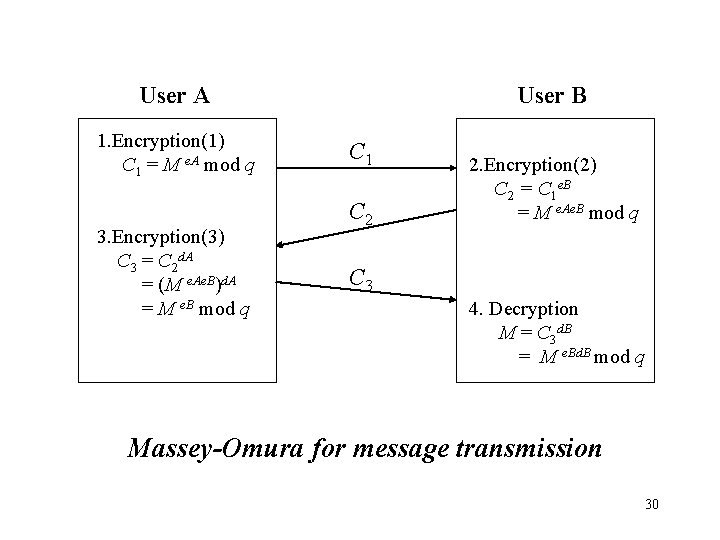
User A 1. Encryption(1) C 1 = M e. A mod q 3. Encryption(3) C 3 = C 2 d. A = (M e. Ae. B)d. A = M e. B mod q User B C 1 C 2 2. Encryption(2) C 2 = C 1 e. B = M e. Ae. B mod q C 3 4. Decryption M = C 3 d. B = M e. Bd. B mod q Massey-Omura for message transmission 30

El. Gamal encryption scheme • Parameters – – – – p : a large prime α: a generator in Zp* a : a private key, a [1, p-1] c : a public key , β = αa (mod p) m : a message, m [1, p-1] k : a random integer that is privately selected, k K = (p, α, a, β) : public key + private key [0, p-2] • Encryption e. K(m, k)=(y 1, y 2) where y 1 = αk mod p and y 2=mβk mod p • Decryption m = d. K(y 1, y 2) = y 2(y 1 a)-1 mod p 31

El. Gamal signature scheme • 1985 El. Gamal • Parameters – – – p : a large prime α: a generator in Zp* a : a private key, a [1, p-1] β : a public key , β = αa (mod p) m : a message to be signed , m [1, p-1] k : a random integer that is privately selected, k [0, p-2] • Signature – r = αk mod p, where gcd( k, p-1 ) = 1 – m = ks + ra mod (p-1) – ( m , (r, s) ) is sent to the verifier • Verification – αm = rsβ r mod p – The signature (r, s) is accepted when the equality holds true. 32