Cryptography Taehyung Kim HPC Lab POSTECH Goals To

Cryptography Taehyung Kim HPC Lab. POSTECH

Goals • To know – – – What is the cryptography? What is a key in cryptography system? What is a symmetric key system? What is a public key system? What is the base of the Public-key cryptography? • To exercise simple cryptography algorithms

Cryptography • Definition – The art of secret writing – Crypto(hidden) + graphy(writing) • Objective – To enable two people to communicate over an insecure channel in such a way that opponent cannot understand what is being said

Cryptography • The mostly used tool for securing information and services • Relies on ciphers: mathematical functions used for encryption and decryption of a message – Encryption – the process of disguising a message in such a way as to hide its substance – Ciphertext – an encrypted message – Decryption – the process of returning an ecrypted message back into plaintext

Ciphers • For some message M • Let’s denote – the encryption of that message into cipher text as Ek(M) = C – the decryption into plain text as Dk(C) = M • Notice, – Symmetric-key algorithm – Public-key algorithm Dk(Ek(M)) = M Dk 1(Ek 2(M))= M

Cryptosystem • Algorithm + Key • The reason for having a key to an algorithm – Difficult to devising new algorithms – Difficult to quickly explain a newly devised algorithm to the person with whom you’d like to start communication securely • A good cryptosystem – Perfectly OK to have everyone know the algorithm – Knowledge of the algorithm without the key does not help unmangle the information

Classical Cryptography • Transposition (permutation) cipher – Simple transposition • Substitution cipher – shift cipher – Polyalphabetic cipher

Simple Transposition • Grouping the plaintext into blocks of t characters • Applying to each block a single permutation on the numbers 1 through t • Encryption – C = E (M) = m (1) …m (t), (M=m 1…mt) • Decryption – M = D (C) = E -1(C) = c -1(1) …c -1(t), (C = c 1…ct)

Simple Transposition Example • T = 6, = (6 4 1 3 5 2) • M = CAESAR – m 1 = C, m 2 = A, m 3 = E, m 4 = S, m 5 = A, m 6 = R – C = m 6 m 4 m 1 m 3 m 5 m 2 = RSCEAA • Exercise – C = OPCYTRYPGAHR , M = ? -1 = (3 6 4 2 5 1) M = D (C) = D ({OPCYTR})D ({YPGAHR}) = CRYPTOGRAPHY

Shift Cipher • A kind of simple substitution ciphers • Example – M = CAESAR • m 1 = C, m 2 = A, m 3 = E, m 4 = S, m 5 = A, m 6 = R – Ci = ( mi + 3) % 26 • C = FDHVDU • General shift cipher – Ci = (a·mi + k) % 26

Polyalphabetic (Vigenere) cipher • Grouping the plaintext into blocks of n characters -> block size = 5 = n • Let E 1, E 2, …, En be distinct substitution ciphers. • To encrypt a plaintext message M, apply the Ei( i=1, 2, …, n) cyclically to the message characters • Encryption – C = E(M) = E 1(m 1)E 2(m 2)…En(mn)E 1(mn+1)…. (M=m 1…mt) • Decryption – M = D(C) = E 1 -1(c 1)E 2 -1(c 2)…En-1(cn)E 1 -1(cn+1)…(C = c 1…ct)

Polyalphabetic Cipher Example • Block size = 3 • E 1, E 2, E 3 are shift ciphers with Key = { 2, 16, 5} • M = CRYPTOGRAPHY ÞC = E 1(C)E 2(R)E 3(Y)E 1(P)E 2(T)E 3(O) E 1(G)E 2(R)E 3(A)E 1(P)E 2(H)E 3(Y) Þ = EHDRJTIHFRXD

Cryptanalysis of a substitution cipher • Letter-frequency in English can be broken into 5 groups: – e (0. 127 most common occurrence); – t, (0. 091), a (0. 082), o (0. 075), i (0. 070), n (0. 067), s (0. 063), h (0. 061), r (0. 060); – d (0. 043), l (0. 040) ; – c (0. 028), u (0. 028), m (0. 024), w (0. 023), f (0. 022), g (0. 020), y (0. 020), p (0. 019), b (0. 015); – v (0. 010), k (0. 008), j (0. 002), x (0. 001), q (0. 001), z (0. 001 least common)

Exercise • Decipher a given ciphertext – Key = { 5, 17, 4, 20 } – C = IVGCUYILFXMPJEGCUYILYVBN

Exercise • Decipher a given ciphertext. ( you first find the block size. Look at the letters applied same substitution cipher, and see which letter occurs most frequently And using letter frequency in English, decipher. ) CHREEVOAHMAERATBIAXXWTNXBEEOPHBSBQMQEQER BWRVXUOAKXAOSXXWEAHBWGJMMQMNKGRFVGXWT RZXWIAKLXFPSKAUTEMNDCMGTSXMXBTUIADNGMGP SRELXNJELXVRVPRTULHDNQWTWDTYGBPHXTFALJH ASVBFXNGLLCHRZBWELEKMSJIKNBHWRJGNMGJSGL XFEYPHAGNRBIEQJTAMRVLCRREMNDGLXRRIMGNSN RWCHRQHAEYEVTAQEBBIPEEWEVKAKOEWADREMXM TBHHCHRTKDNVRZCHRCLQOHPWQAIIWXNRMGWOIIF KEE

Public Key Cryptography • Problem with symmetric key algorithms – A secure method of telling your partner the key – A separate key for everyone you might communicate with • Public-Key algorithms use a public-key and private-key pair over a message
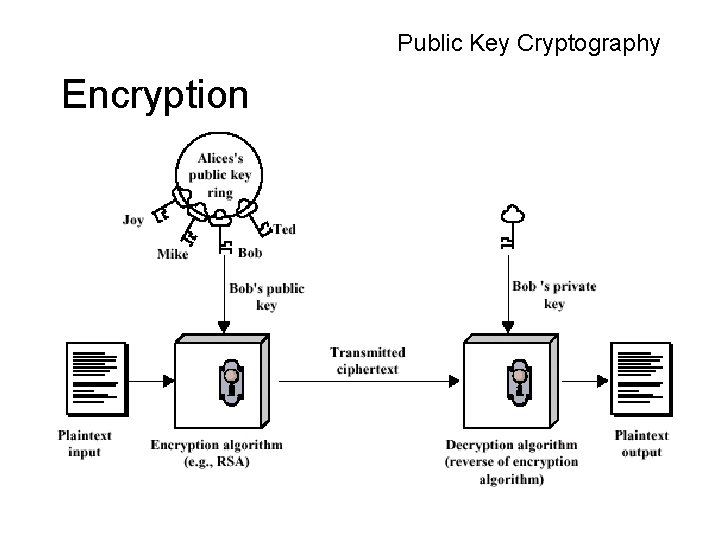
Public Key Cryptography Encryption
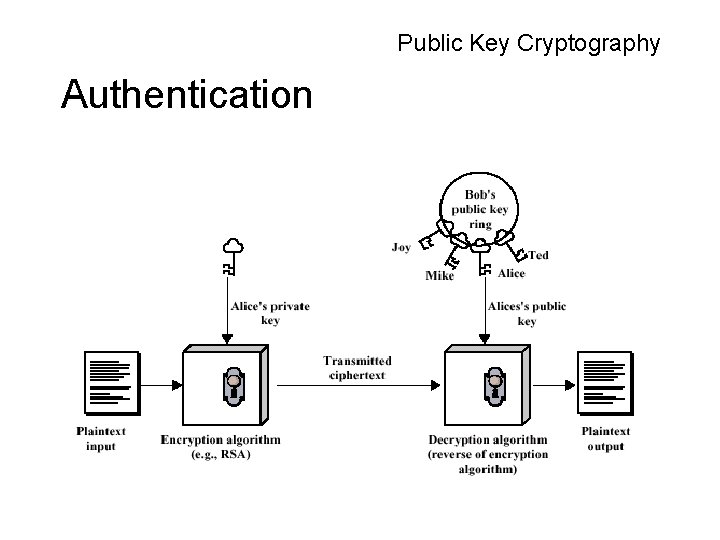
Public Key Cryptography Authentication

RSA Public-key encryption • Proposed by Rivest, Shamir, and Adleman in 1977 • Mostly widely used public-key cryptosystem • The security is based on the intractability of the integer factorization problem

RSA Public Key Cryptography Key Generation • Generate two large random primes p and q. • Compute n = pq and = (p-1)(q-1). • Select a random integer e, 1 < e < , such that gcd(e, ) = 1. • Compute the unique integer d, 1 < d < , such that ed 1 (mod ). Public key : (n, e) Private key : d

RSA Public Key Cryptography Encryption • Bob encrypts a message m for Alice – Obtain Alice’s public key (n, e) – Represent the message as an integer m in the interval [0, n-1] – Compute C Me (mod n) • Alice recovers plaintext m from c as follows: – M Cd (mod n)

RSA Public Key Cryptography Theorem: C Md (mod n) • Proof Cd (Me)d (mod n) Med (mod n) Mk +1 (mod n) MMk(p-1)(q-1) (mod n) M (mod n)

RSA Public Key Cryptography Example • • • p = 2357, q = 2251 n = pq = 6012707, = (p-1)(q-1) = 6007800 Choose e = 3674911, then d = 422191 Public key (n = 6012707, e = 3674911) Private key d = 422191 Plaintext m = 5234673 C = me mod n = 52346733674911 mod 6012707 = 3650502
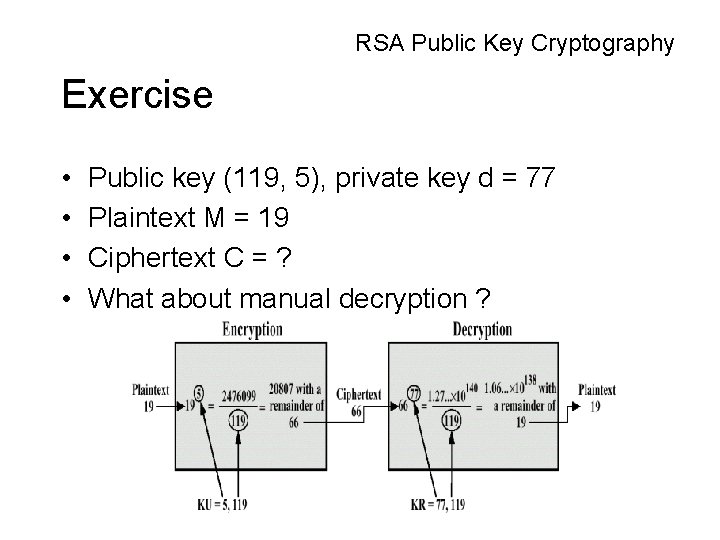
RSA Public Key Cryptography Exercise • • Public key (119, 5), private key d = 77 Plaintext M = 19 Ciphertext C = ? What about manual decryption ?

RSA Public Key Cryptography Exercise • Find five prime integer more than 1000 • Make a public key and a private key – Two primes, p and q, must be less than 1000 • Select a plaintext and cipher it using your public key • Decipher the other group’s ciphertext

Cryptography

How to determine a block size • Kasiski's method: 1. Find all repeated strings in ciphertext of length at least 3 2. Compute distances between them 3. Block size will be a common divisor of those numbers

Letter-frequency • e (0. 127 most common occurrence); • t, (0. 091), a (0. 082), o (0. 075), i (0. 070), n (0. 067), s (0. 063), h (0. 061), r (0. 060); • d (0. 043), l (0. 040) ; • c (0. 028), u (0. 028), m (0. 024), w (0. 023), f (0. 022), g (0. 020), y (0. 020), p (0. 019), b (0. 015); • v (0. 010), k (0. 008), j (0. 002), x (0. 001), q (0. 001), z (0. 001 least common)

Answer • • A: 7 B: 6 C: 6 D: 4 E: 1 F: 2 G: 0 H: 0 I: 1 J: 2 K: 1 L: 0 M: 2 N: 4 O: 0 P: 1 Q: 4 R: 3 S: 0 T: 2 U: 1 V: 1 W: 9 X: 5 Y: 0 Z: 0 • • A: 3 B: 1 C: 0 D: 3 E: 9 F: 2 G: 3 H: 5 I: 3 J: 0 K: 0 L: 0 M: 2 N: 6 O: 6 P: 1 Q: 0 R: 3 S: 7 T: 5 U: 1 V: 1 W: 1 X: 0 Y: 0 Z: 0 • • A: 5 B: 2 C: 1 D: 0 E: 2 F: 0 G: 4 H: 3 I: 3 J: 3 K: 0 L: 2 M: 0 N: 5 O: 1 P: 2 Q: 4 R: 13 S: 1 T: 2 U: 2 V: 4 W: 0 X: 1 Y: 2 Z: 0 • • A: 1 B: 1 C: 1 D: 0 E: 10 F: 0 G: 1 H: 3 I: 4 J: 2 K: 4 L: 4 M: 8 N: 0 O: 0 P: 3 Q: 2 R: 3 S: 1 T: 1 U: 0 V: 3 W: 3 X: 4 Y: 1 Z: 2 • • A: 3 B: 5 C: 0 D: 0 E: 2 F: 2 G: 7 H: 6 I: 0 J: 0 K: 4 L: 6 M: 5 N: 0 O: 0 P: 1 Q: 0 R: 2 S: 0 T: 4 U: 0 V: 1 W: 3 X: 10 Y: 0 Z: 1 • THEALMONDTREEWASINTENTATIVEBLOSSOMTHEDAYSWERELONGEROFTENENDINGWITHMAGN IFICENTEVENINGSOFCORRUGATEDPINKSKIESTHEHUNTINGSEASONWASOVERWITHHOUNDSAN DGUNSPUTAWAYFORSIXMONTHSTHEVINEYARDSWEREBUSYAGAINASTHEWELLORGANIZEDFAR MERSTREATEDTHEIRVINESANDTHEMORELACKADAISICALNEIGHBORSHURRIEDTODOTHEPRUNI NGTHEYSHOULDHAVEDONEINNOVEMCALORBUSINESSRIVALSE
- Slides: 29