Cryptography Lecture 5 Perfect indistinguishability Let Gen Enc

Cryptography Lecture 5

Perfect indistinguishability • Let =(Gen, Enc, Dec) be an encryption scheme with message space M, and let A be an adversary/algorithm • Define a randomized exp’t Priv. KA, : 1. A outputs m 0, m 1 M 2. k Gen, b {0, 1}, c Enck(mb) 3. b’ A(c) Challenge ciphertext Adversary A succeeds if b = b’, and we say the experiment evaluates to 1 in this case

Perfect indistinguishability • Easy to succeed with probability ½ … • Scheme is perfectly indistinguishable if for all attackers (algorithms) A, it holds that Pr[Priv. KA, = 1] = ½

Perfect indistinguishability • Claim: is perfectly indistinguishable is perfectly secret • I. e. , perfect indistinguishability is just an alternate definition of perfect secrecy

Computational secrecy? • Idea: relax perfect indistinguishability • Two approaches – Concrete security – Asymptotic security

Computational indistinguishability (concrete) • (t, )-indistinguishability: – Security may fail with probability ≤ – Restrict attention to attackers running in time ≤ t • Or, t CPU cycles

Computational indistinguishability (concrete version) • is (t, )-indistinguishable if for all attackers A running in time at most t, it holds that Pr[Priv. KA, = 1] ≤ ½ + • Note: ( , 0)-indistinguishable = perfect indistinguishability – Relax definition by taking t < and > 0

Concrete security • Parameters t, are what we ultimately care about in the real world • Does not lead to a clean theory. . . – Sensitive to exact computational model – can be (t, )-secure for many choices of t, • Would like to have schemes where users can adjust the achieved security as desired

Asymptotic security • Introduce security parameter n – For now, think of n as the key length – Chosen by honest parties when they generate/share key • Allows users to tailor the security level – Known by adversary • Measure running times of all parties, and the success probability of the adversary, as functions of n

Computational indistinguishability (asymptotic) • Computational indistinguishability: – Security may fail with probability negligible in n – Restrict attention to attackers running in time (at most) polynomial in n

Definitions • A function f: Z+ is polynomial if there exists c such that f(n) < nc • A function f: Z+ [0, 1] is negligible if for every polynomial p it holds that f(n) < 1/p(n) for large enough n – I. e. , decays faster than any inverse polynomial – Typical example: f(n) = poly(n)∙ 2 -cn

Why these specific choices? • Somewhat arbitrary • “Efficient” = “probabilistic polynomial-time (PPT)” borrowed from complexity theory • Convenient closure properties – Poly * poly = poly • A PPT algorithm making calls to PPT subroutines is PPT – Poly * negligible = negligible • Poly-many calls to subroutines that fail with negligible probability overall

(Re)defining encryption • A private-key encryption scheme is defined by three PPT algorithms (Gen, Enc, Dec): – Gen: takes as input 1 n; outputs k. (Assume |k|≥n. ) – Enc: takes as input a key k and message m {0, 1}*; outputs ciphertext c c Enck(m) – Dec: takes key k and ciphertext c as input; outputs a message m or “error”

Computational indistinguishability (asymptotic version) • Fix a scheme and some adversary A • Define a randomized exp’t Priv. KA, (n): 1. A(1 n) outputs m 0, m 1 {0, 1}* of equal length 2. k Gen(1 n), b {0, 1}, c Enck(mb) 3. b’ A(c) Adversary A succeeds if b = b’, and we say the experiment evaluates to 1 in this case

Computational indistinguishability (asymptotic version) • is computationally indistinguishable (aka EAV-secure) if for all PPT attackers A, there is a negligible function such that Pr[Priv. KA, (n) = 1] ≤ ½ + (n)

Example 1 • Consider a scheme where Gen(1 n) generates a uniform n-bit key, and the best attack is bruteforce search of the key space – So if A runs in time t(n), then Pr[Priv. KA, (n) = 1] < ½ + O(t(n)/2 n) • This scheme is EAV-secure! For any polynomial t, the function t(n)/2 n is negligible

Example 2 • Consider a scheme and a particular attacker A that runs for n 3 minutes and breaks the scheme with probability 240 2 -n – This does not contradict asymptotic security – What about real-world security (against this particular attacker)? • n=40: A breaks scheme with prob. 1 in 6 weeks • n=50: A breaks scheme with prob. 1/1000 in 3 months • n=500: A breaks scheme with prob. 2 -500 in 200 years

Example 3 • What happens when computers get faster? • E. g. , consider a scheme that takes time n 2 to run but time 2 n to break with prob. 1 • What if computers get 4 faster? – Honest users double n and can thus maintain the same running time – Time to break scheme is squared! • Time required to break the scheme increases

Encryption and plaintext length • In practice, we want encryption schemes that can encrypt arbitrary-length messages • Encryption does not hide the plaintext length (in general) – The definition takes this into account by requiring m 0, m 1 to have the same length • But beware that leaking plaintext length can often lead to problems in the real world! – Obvious examples… – Database searches – Encrypting compressed data

Computational secrecy • From now on, we will assume the computational setting by default – Usually, the asymptotic setting

Pseudorandomness

Pseudorandomness • Important building block for computationally secure encryption • Important concept in cryptography

What does “random” mean? • What does “uniform” mean? • Which of the following is a uniform string? – 01010101 – 001011100110 – 00000000 • If we generate a uniform 16 -bit string, each of the above occurs with probability 2 -16

What does “uniform” mean? • “Uniformity” is not a property of a string, but a property of a distribution • A distribution on n-bit strings is a function D: {0, 1}n [0, 1] such that x D(x) = 1 – The uniform distribution on n-bit strings, denoted Un, assigns probability 2 -n to every x {0, 1}n

What does “pseudorandom” mean? • Informal: cannot be distinguished from uniform (i. e. , random) • Which of the following is pseudorandom? – 01010101 – 001011100110 – 00000000 • Pseudorandomness is a property of a distribution, not a string

Pseudorandomness (take 1) • Fix some distribution D on n-bit strings – x D means “sample x according to D” • Historically, D was considered pseudorandom if it “passed a bunch of statistical tests” – Prx D[1 st bit of x is 1] ½ – Prx D[parity of x is 1] ½ – Prx D[Testi(x)=1] Prx Un[Testi(x)=1] for i = 1, …

Pseudorandomness (take 2) • This is not sufficient in an adversarial setting! – Who knows what statistical test an attacker will use? • Cryptographic def’n of pseudorandomness: – D is pseudorandom if it passes all efficient statistical tests

Pseudorandomness (concrete) • Let D be a distribution on p-bit strings • D is (t, )-pseudorandom if for all A running in time at most t, | Prx D[A(x)=1] - Prx Up[A(x)=1] | ≤

Pseudorandomness (asymptotic) • Security parameter n, polynomial p • Let Dn be a distribution over p(n)-bit strings • Pseudorandomness is a property of a sequence of distributions {Dn} = {D 1, D 2, … }

Pseudorandomness (asymptotic) • {Dn} is pseudorandom if for all probabilistic, polynomial-time distinguishers A, there is a negligible function such that | Prx Dn[A(x)=1] - Prx Up(n)[A(x)=1] | ≤ (n)

Pseudorandom generators (PRGs) • A PRG is an efficient, deterministic algorithm that expands a short, uniform seed into a longer, pseudorandom output – Useful whenever you have a “small” number of true random bits, and want lots of “randomlooking” bits

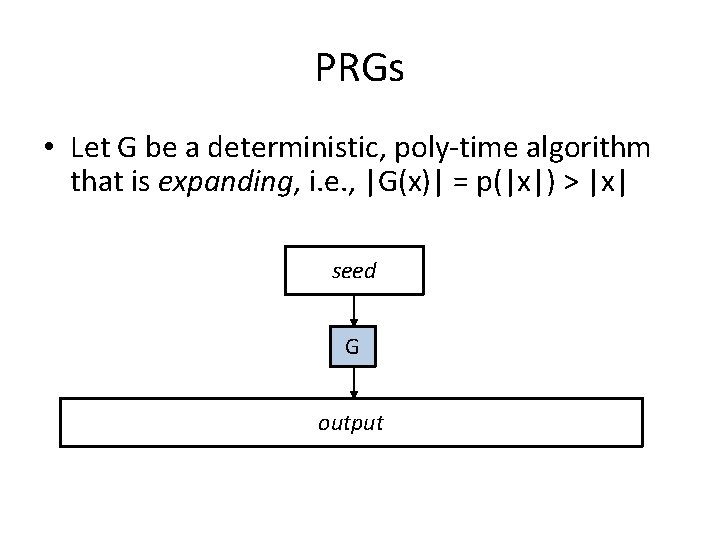
PRGs • Let G be a deterministic, poly-time algorithm that is expanding, i. e. , |G(x)| = p(|x|) > |x| seed G output