Cryptography in Constant Parallel Time Benny Applebaum Technion

Cryptography in Constant Parallel Time Benny Applebaum (Technion Princeton) Talk based on joint works with Yuval Ishai and Eyal Kushilevitz (FOCS 04, CCC 05, RANDOM 06, CRYPTO 07)

Talk Outline • Part 1: Crypto in NC 0 – Survey -The basic question - Main results - Main tool: randomized encoding of functions • Part 2: Crypto in CN 0 -The basic question - Main results - “Something” about the proof [AIK 07]

Part 1: Crypto in NC 0 Encryption Signature ZK-Proofs

Efficiency of Cryptographic Primitives • Q: What computational resources are needed for cryptography? • Can cryptographic primitives be computed by very simple functions? NC 03 Simple = each output bit depends on O(1) input bits = const. depth circuits with bounded fan-in = NC 0 • Currently the smallest creature in the complexity zoo NC 0

Cryptography in NC 0? • Longstanding open question Håstad 87 Impagliazzo Naor 89 Goldreich 00 Cryan Miltersen 01 Krause Lucks 01 Mossel Shpilka Trevisan 03 • Real-life motivation: super-fast cryptographic hardware • Tempting conjecture: [CM]: Yes crypto hardness “complex” function [G]: No

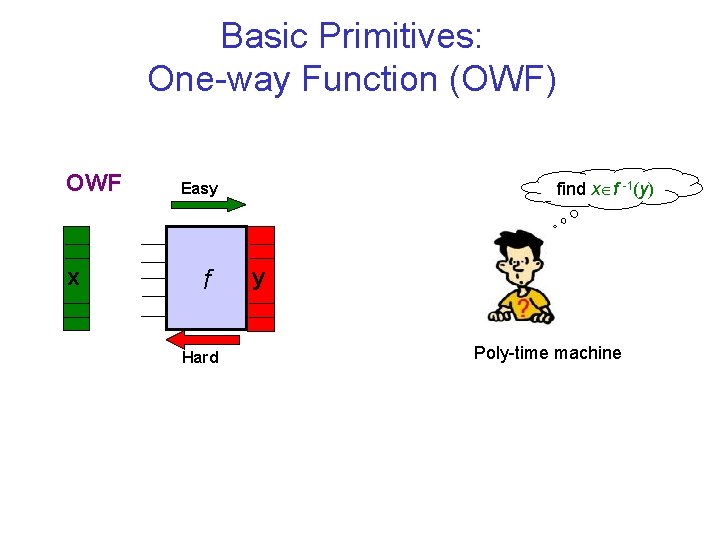
Basic Primitives: One-way Function (OWF) OWF x find x f -1(y) Easy f Hard y Poly-time machine

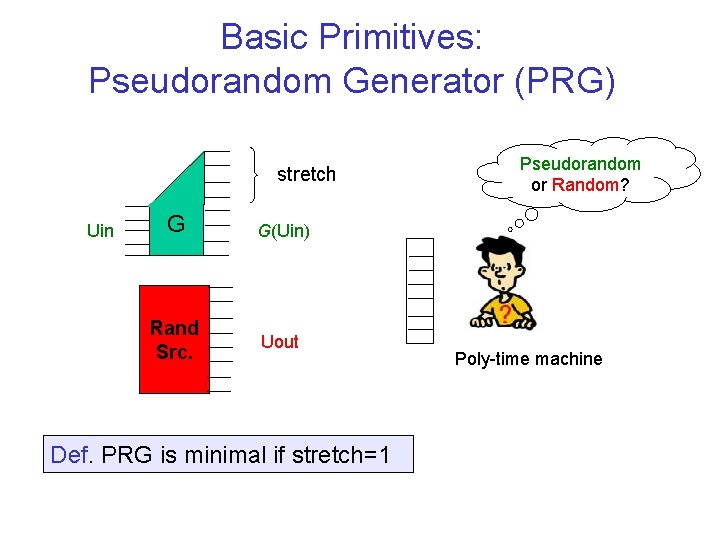
Basic Primitives: Pseudorandom Generator (PRG) stretch Uin G G(Uin) Rand Src. Uout Def. PRG is minimal if stretch=1 Pseudorandom or Random? Poly-time machine

Previous Work • Negative Positive results 1 from 0 [Goldreich – No PRG OWF in NC 00, Cryan Miltersen lattices… 01] 2 factoring, discrete-log, – No PRF PRG in with NC 1 large from factoring stretch in [Naor NC 03, Reingold NC 04 [CM 01, 97] Mossel. Shpilka. Trevisan 03] – PRG (sub-lin stretch) in AC 0 from subset sum [Impagliazzo Naor 89] • Permutation in NC 0 which is P-complete to invert [Håstad 87] • Function in NC 0 which is NP-complete to invert [Agrawal Allender Rudich 98] • Heuristic construction of OWF/PRG in NC 0 [Goldreich 00 MST 03 ] NC 1 AC 0 NC 0 factoring, discrete-log, lattices, … subset sum impossible low stretch NC 04 NC 03 NC 02 PRG / OWF open

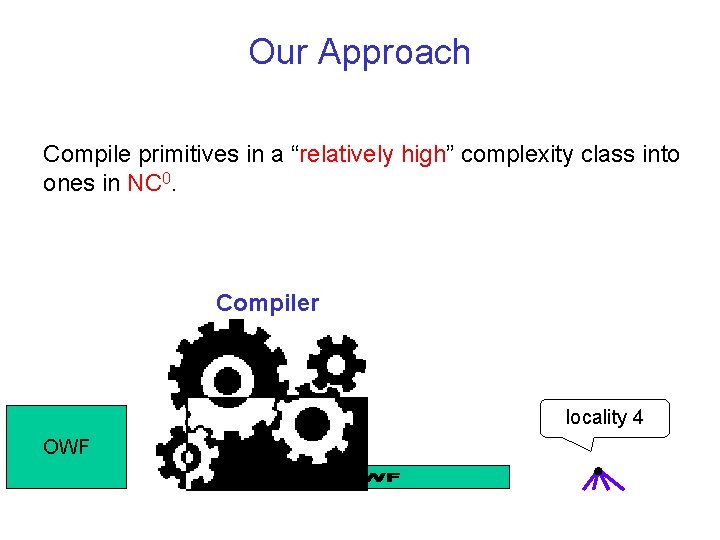
Our Approach Compile primitives in a “relatively high” complexity class into ones in NC 0. Compiler locality 4 OWF

Our Results

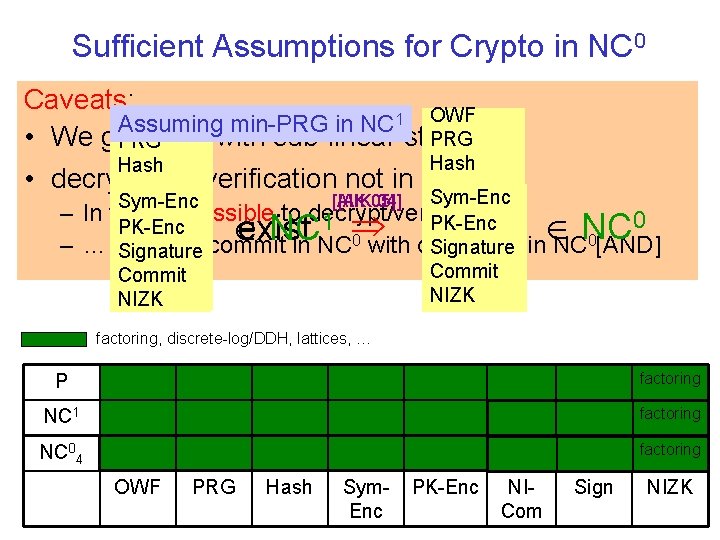
Sufficient Assumptions for Crypto in NC 0 Caveats: OWF Assuming min-PRG in NC 1 OWF PRG • We get PRG with sub-linear stretch PRG Hash • decryption / verification not in NC 0… – – Sym-Enc 0 [AIK 05] 04] [AIK Sym-Enc In fact, impossible to decrypt/verify in NC 1 PK-Enc … But: can commit in NC 0 with decommit Signature in Signature Commit NIZK 0 NCNC [AND] exist NC 0 factoring, discrete-log/DDH, lattices, … P factoring NC 1 factoring NC 04 factoring OWF PRG Hash Sym. Enc PK-Enc NICom Sign NIZK

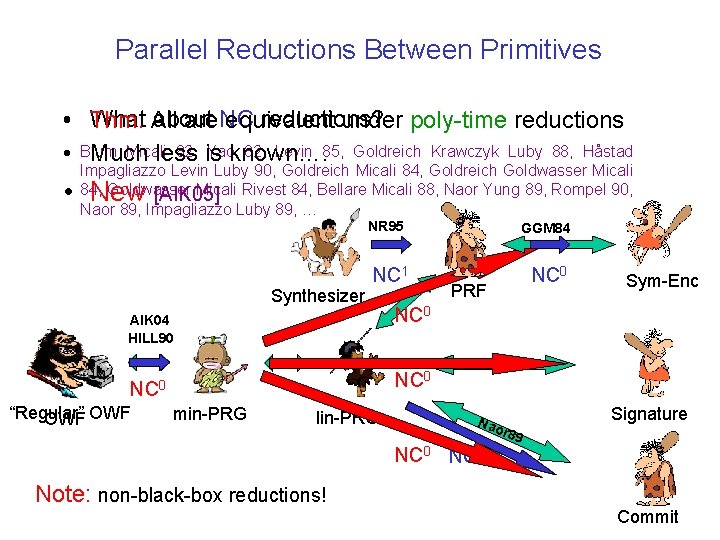
Parallel Reductions Between Primitives What All about reductions? • Thm. are. NC equivalent under poly-time reductions Micali 82, is Yaoknown…. 82, Levin 85, Goldreich Krawczyk Luby 88, Håstad • Blum Much less Impagliazzo Levin Luby 90, Goldreich Micali 84, Goldreich Goldwasser Micali 84, Goldwasser Micali Rivest 84, Bellare Micali 88, Naor Yung 89, Rompel 90, [AIK 05] Naor 89, Impagliazzo Luby 89, … • New NR 95 NC 1 Synthesizer AIK 04 HILL 90 NC 0 PRF Sym-Enc NC 0 NC 10 “Regular” OWF GGM 84 min-PRG lin-PRG Nao r 89 Signature NC 0 Note: non-black-box reductions! Commit

PRG with large stretch in NC 0 • Our techniques give a PRG with sub-linear stretch - E. g. , stretches n bits to n+n 0. 5 bits • Question: Are there PRGs in NC 0 with large stretch ? - E. g. , linear stretch, G: {0, 1}n {0, 1}2 n (LPRG) • Motivation: parallel stream ciphers • Related work: - No Super-Linear PRG in NC 03, NC 04 [CM 01, MST 03] - Heuristic Super-Linear PRG in NC 05 [MST 03]

PRG with large stretch in NC 0 • Question: Are there PRGs in NC 0 with large stretch ? • Thm. [AIK 06]: LPRG in NC 0 - from Algebraic assumption of [Alekhnovich 03] - (easily) implies Inapporximability of MAX 3 SAT (no PCP!) - unlikely to be constructed via “compiler”

Our Techniques

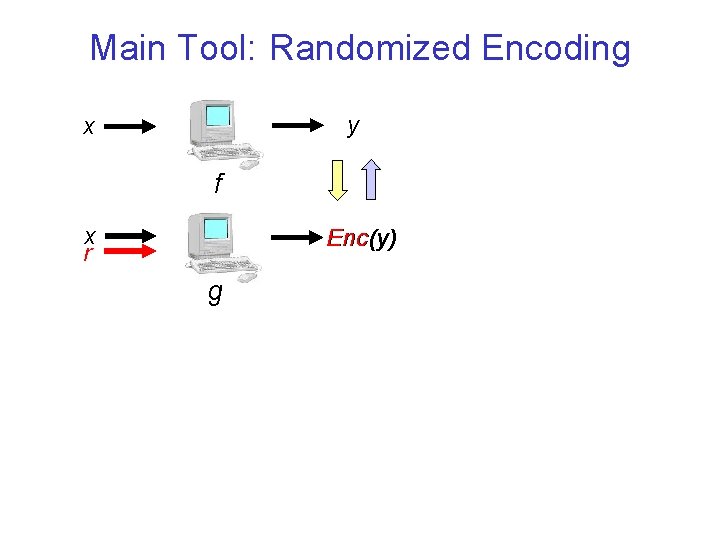
Main Tool: Randomized Encoding y x f x r Enc(y) g

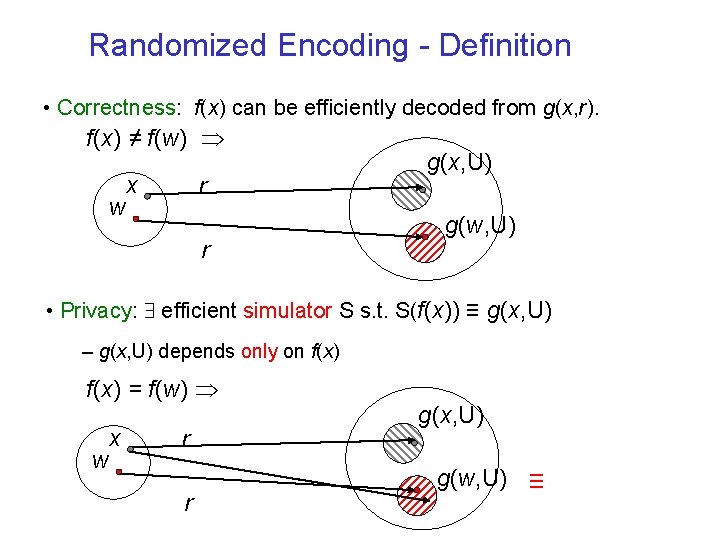
Randomized Encoding - Definition • Correctness: f(x) can be efficiently decoded from g(x, r). f(x) ≠ f(w) w x r r g(x, U) g(w, U) • Privacy: efficient simulator S s. t. S(f(x)) ≡ g(x, U) – g(x, U) depends only on f(x) = f(w) w x r r g(x, U) g(w, U) ≡

Randomized Encoding – Cont. • Explicitly introduced by Ishai and Kushilevitz [IK 00] – Algebraic framework of randomizing polynomials – Motivation: information-theoretic secure multiparty computation – Weaker versions implicit in secure computation (e. g. [Kil 88, FKN 94]) • g is a “randomized encoding” of f – Nontrivial relaxation of computing f • Want relaxation to be – Secure: g inherits security properties of f – Liberal: even “complex” f admit encodings g NC 0

Security of Randomized Encoding • Thm. [AIK 04]: preserves crypto hardness of most primitives – E. g. , OWF, OWP, PRG, Sym-Enc, PK-Enc, Sign, MAC, Hash, Com, ZK – Also works for information-theoretic primitives ( -biased gens, extractors, …) – Different primitives require different variants of randomized encoding • Paradigm for crypto w/low complexity: – Encode functions in complexity class HIGH by functions in LOW – Show that a primitive P can be implemented in HIGH – Conclude that P can be implemented in LOW

Part 2: Crypto in CN 0 [AIK 07]

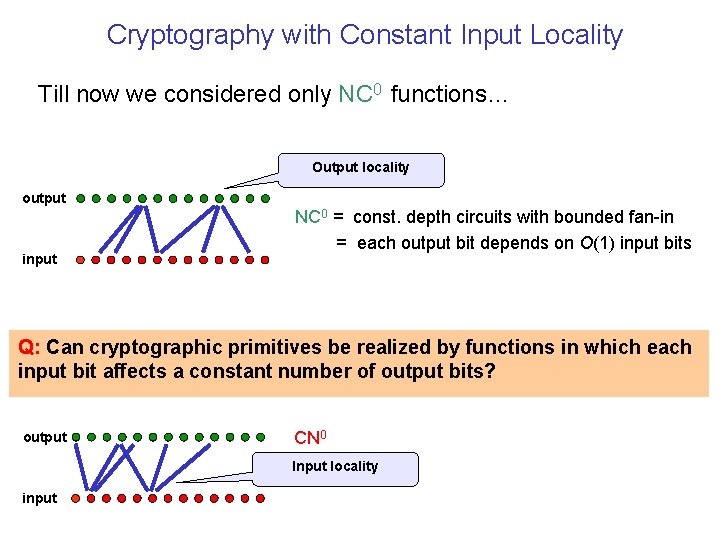
Cryptography with Constant Input Locality Till now we considered only NC 0 functions… Output locality output input NC 0 = const. depth circuits with bounded fan-in = each output bit depends on O(1) input bits Q: Can cryptographic primitives be realized by functions in which each input bit affects a constant number of output bits? output CN 0 Input locality input

Motivation I: Avalanche Property Confusion/Diffusion, Avalanche [Shannon 49, Feistel 73]: input-output dependencies of a block cipher should be “complex” “The important fact is that all output digits have potentially become very involved functions of all input digits” [Feistel 73] Easily justified in block ciphers (or pseudorandom functions/permutations). Is it also true for other primitives? output CN 0 Input locality input

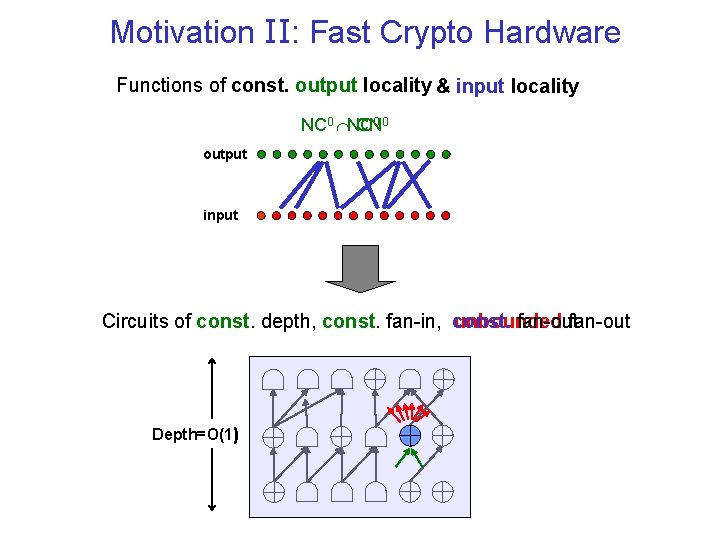
Motivation II: Fast Crypto Hardware Functions of const. output locality & input locality NC 0 NC CN 0 0 output input Circuits of const. depth, const. fan-in, const. unbounded fan-out Depth=O(1)

Motivation III: Complexity Theory Bounded-occurrence k-Constraint Satisfaction Problem – X 1 +X 3 X 5 =0 – X 2 X 3 X 4 =1. . . - X 2 +X 3 + X 4 =1 • Goal: • Fact: • List of constraints over n variables x 1, …, xn • Each constraint involves k=O(1) variables • Each variable appears in O(1) constraints Find a satisfying assignment Still Hard in many aspects: – Cook-Levin Theorem [C 71, L 73]: – – – NP-hard [C 71]: Still NP-hard PCP Theorem [ALMSS, AS 92]: NP-hard to approximate [PY 88]: Still NP-hard to approximate OWF in NC 0 [AIK 04]: “Cryptographically-hard” Still “Cryptographically-hard” ? OWF in NC 0 CN 0 YES

Previous Work Heuristic OWF in NC 0 CN 0 • [Mossel Shpilka Trevisan 03]0 Heuristic PRG in NC Crypto in CN under standard assumptions? • [AIK 04] Primitives in NC 0 from primitives in NC 1 • [Goldreich 00] – Primitives in NC 1 from standard assumptions (e. g. , factoring, DLOG, lattices) OWFs, PRGs, Encryption, Signatures, Hash… in NC 0 from factoring • [AIK 06] Linear PRG in NC 0 CN 0 from Assumption of [Alekhnovich 03] Factoring most prims NC 0 Rand linear code Mc. Eliece Alekhnovich’s assumption Heuristic construction PRG OWF PRG CN 0

Main Result A characterization of crypto tasks computable in CN 0 Possible in CN 0 NC 0 Impossible in CN 0 • One-Way Functions* • Message Authentication Codes • Pseudorandom Generators * • Signatures • Commitment Schemes* • Non-Malleable Encryption • Semantically-Secure Encryption (symmetric, public-key) (symmetric* , public-key **) * If hard to decode random binary linear code / learn parity w/noise ** If hard to break Mc. Eliece cryptosystem

Previous Work Heuristic OWF in NC 0 CN 0 • [Mossel Shpilka Trevisan 03]0 Heuristic PRG in NC Crypto in CN under standard assumptions? • [AIK 04] Primitives in NC 0 from primitives in NC 1 • [Goldreich 00] – Primitives in NC 1 from standard assumptions (e. g. , factoring, DLOG, lattices) OWFs, PRGs, Encryption, Signatures, Hash… in NC 0 from factoring • [AIK 06] Linear PRG in NC 0 CN 0 from Assumption of [Alekhnovich 03] Factoring Rand linear code OWF PRG Com PK Enc Mc. Eliece Alekhnovich’s assumption Heuristic construction NC 0 most prims PRG OWF PRG CN 0

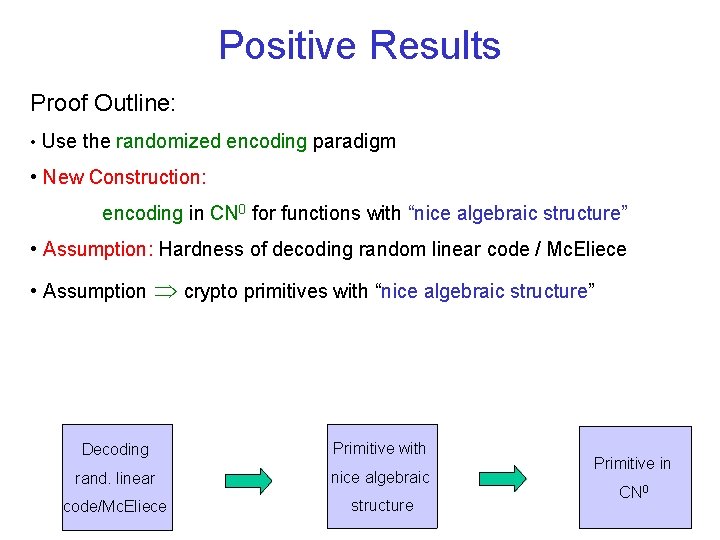
Positive Results Proof Outline: • Use the randomized encoding paradigm • New Construction: encoding in CN 0 for functions with “nice algebraic structure” • Assumption: Hardness of decoding random linear code / Mc. Eliece • Assumption crypto primitives with “nice algebraic structure” Decoding Primitive with rand. linear nice algebraic code/Mc. Eliece structure Primitive in CN 0

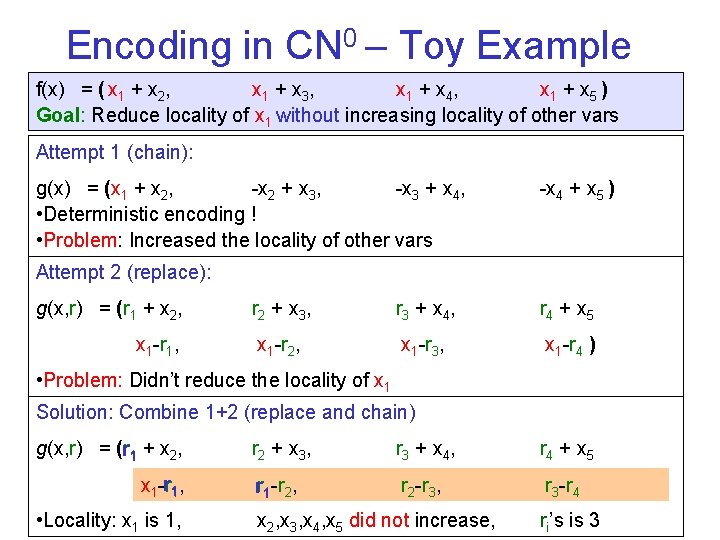
Encoding in CN 0 – Toy Example f(x) = ( x 1 + x 2, x 1 + x 3, x 1 + x 4, x 1 + x 5 ) Goal: Reduce locality of x 1 without increasing locality of other vars Attempt 1 (chain): g(x) = (x 1 + x 2, -x 2 + x 3, -x 3 + x 4, • Deterministic encoding ! • Problem: Increased the locality of other vars -x 4 + x 5 ) Attempt 2 (replace): g(x, r) = (r 1 + x 2, x 1 -r 1, r 2 + x 3 , r 3 + x 4 , r 4 + x 5 x 1 -r 2, x 1 -r 3, x 1 -r 4 ) • Problem: Didn’t reduce the locality of x 1 Solution: Combine 1+2 (replace and chain) g(x, r) = (rr 1 + x 2, x 1 -rr 1, • Locality: x 1 is 1, r 2 + x 3 , r 3 + x 4 , r 4 + x 5 xrr 11 -r -r 22, , rx 21 -r-r 33, , rx 31 -r-r 44 ) x 2, x 3, x 4, x 5 did not increase, ri’s is 3

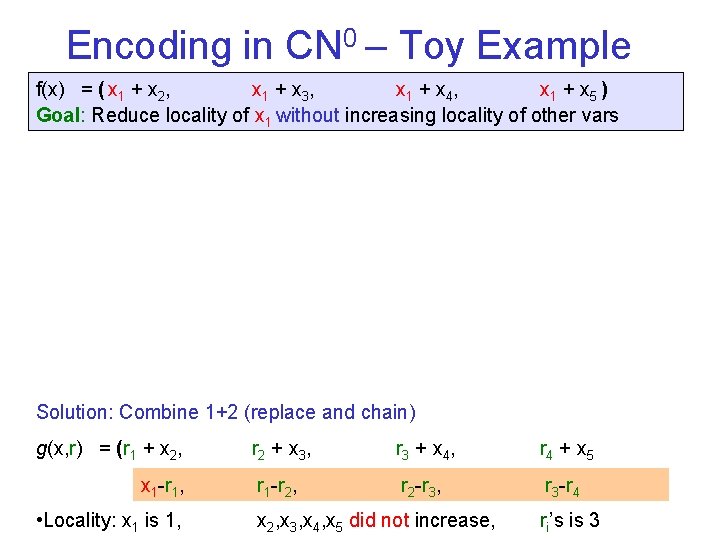
Encoding in CN 0 – Toy Example f(x) = ( x 1 + x 2, x 1 + x 3, x 1 + x 4, x 1 + x 5 ) Goal: Reduce locality of x 1 without increasing locality of other vars Solution: Combine 1+2 (replace and chain) g(x, r) = (r 1 + x 2, x 1 -r 1, • Locality: x 1 is 1, r 2 + x 3 , r 3 + x 4 , r 4 + x 5 r 1 -r 2, r 2 -r 3, r 3 -r 4 x 2, x 3, x 4, x 5 did not increase, ri’s is 3

Encoding in CN 0 – Toy Example f(x) = ( x 1 + x 2, x 1 + x 3, xx 11+x + x 44, x 1 + x 5 ) Goal: Reduce locality of x 1 without increasing locality of other vars Solution: Combine 1+2 (replace and chain) g(x, r) = (r 1 + x 2, x 1 -r 1, r 2 + x 3 , r 3 + x 4 , r 4 + x 5 r 1 -r 2, r 2 -r 3, r 3 -r 4 • Correctness: To decode, add the corresponding entries. • Privacy: g(x, r) distributed uniformly under correctness constraint. By iterating the basic gadget for every variable Corollary: every linear function can be encoded by function w/input locality 3

Encoding in CN 0 – Generalization • Suppose that f is given in some additive form. • f(x)= (x 1 x 2+x 2 x 3 x 5, x 1 x 2+x 2 x 4 x 5, x 1 x 2+x 1 x 3 x 4, x 1 x 2+x 2 x 5) • rank(xi)= # of distinct terms in which xi appears • Thm. f can be encoded by g such that: – input locality of xi is rank(xi) rank(x 1)= 2 – input locality of random inputs is at most 3. – output locality is not increased. Proof: Generalize previous • • Tightness: Some functions cannotconstruction. be encoded with locality < rank(xi) 0 (even w/non-efficient Some functions in CN • Corollary: If forcannot everybei, encoded rank(xi)= O(1) g is in CN 0 encoding). – Unlike NC 0 : “every f has (non-efficient) encoding in NC 0 “ [AIK 04] • [AIK 04] If also algebraic degree = O(1) g is in CN 0 NC 0

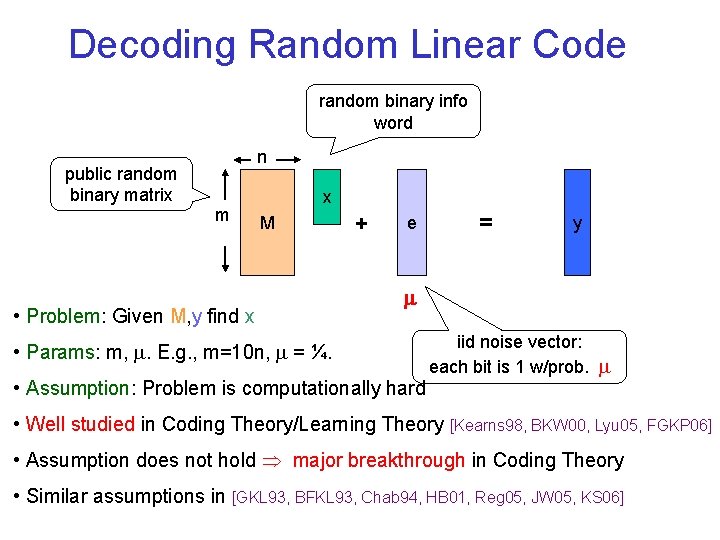
Decoding Random Linear Code random binary info word public random binary matrix n m x M • Problem: Given M, y find x + e = y • Params: m, . E. g. , m=10 n, = ¼. • Assumption: Problem is computationally hard iid noise vector: each bit is 1 w/prob. • Well studied in Coding Theory/Learning Theory [Kearns 98, BKW 00, Lyu 05, FGKP 06] • Assumption does not hold major breakthrough in Coding Theory • Similar assumptions in [GKL 93, BFKL 93, Chab 94, HB 01, Reg 05, JW 05, KS 06]

Decoding Random Linear Code ei= r 2 i-1 r 2 i n m x M + e = y • Problem has nice algebraic structure: linear function + some low-degree noise • Can be used to construct primitives with low rank and low degree - e. g. , OWF, PRG, Commitment

Conclusions • Cryptography in constant parallel time is possible • Randomized encodings (of various types) are useful for this problem (and others…, e. g. MPC) Future Directions: • Better encodings ? ? • Better implementations ? ? • Better (weaker) assumptions ? ? • More applications of randomized encoding ? ?

Thank You !