Cryptography Funny and serious stuff The language of

Cryptography Funny and serious stuff

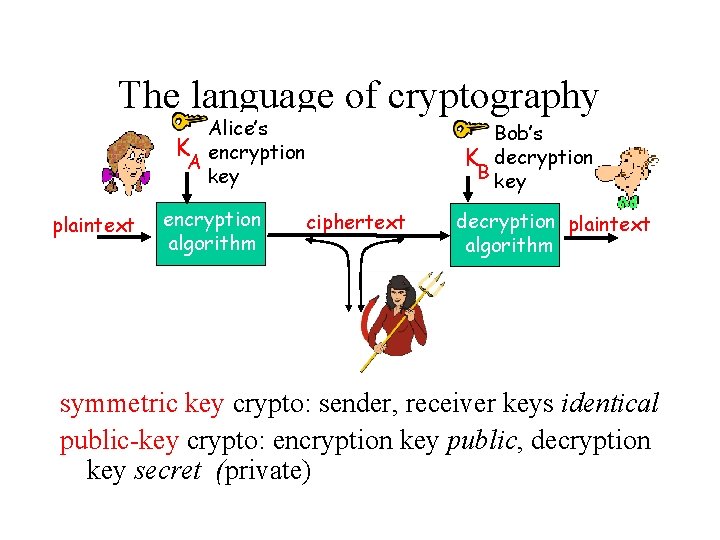
The language of cryptography Alice’s K encryption A key plaintext encryption algorithm Bob’s K decryption B key ciphertext decryption plaintext algorithm symmetric key crypto: sender, receiver keys identical public-key crypto: encryption key public, decryption key secret (private)

Symmetric key cryptography Substitution cipher: substituting one thing for anothere. g. Caesar cipher substituting every letter of a plaintext by a letter that is K letters later (allowing wrap around). For example if K = 3 than the letter “a” in plaintext becomes “d” in ciphertext. Value of K serves as the key. This cipher is pretty easy to break as there are only 25 possible key values.

Symmetric key cryptography Improvement over the Caesar cipher is monoalphabetic cipher: substitute one letter for another but without a specific pattern : plaintext: abcdefghijklmnopqrstuvwxyz ciphertext: mnbvcxzasdfghjklpoiuytrewq E. g. : Plaintext: bob. i love you. alice ciphertext: nkn. s gktc wky. mgsbc Q: How hard to break this simple cipher? : q brute force (how hard? ) q other?

Symmetric key cryptography • Polyalphabetic encryption – Using multiple monoalphabetic ciphers, with a specific monoalphabetic cipher to encode a letter in a specific position in the plaintext message. For example we may use two Caesar ciphers with k 1 =5 and k 2=19 in repeating pattern C 1, C 2, C 1, C 2 To break such a cipher it is necessary to know the keys and the pattern.

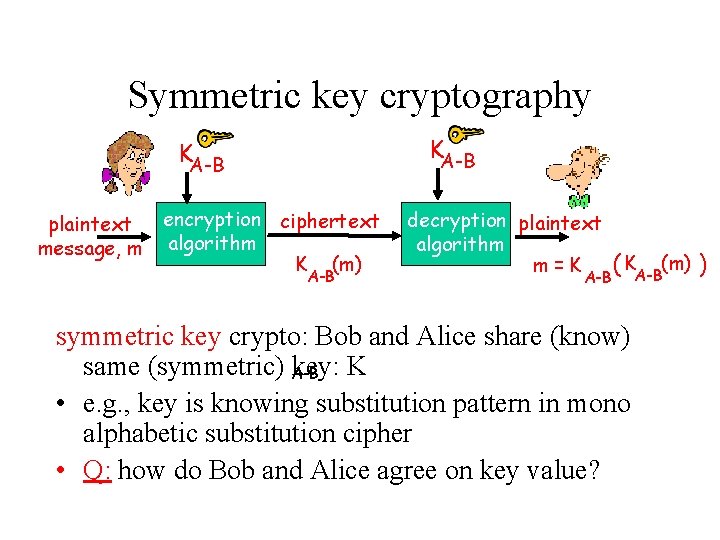
Symmetric key cryptography KA-B plaintext message, m encryption ciphertext algorithm K (m) A-B decryption plaintext algorithm m=K A-B ( KA-B(m) ) symmetric key crypto: Bob and Alice share (know) same (symmetric) A-B key: K • e. g. , key is knowing substitution pattern in mono alphabetic substitution cipher • Q: how do Bob and Alice agree on key value?

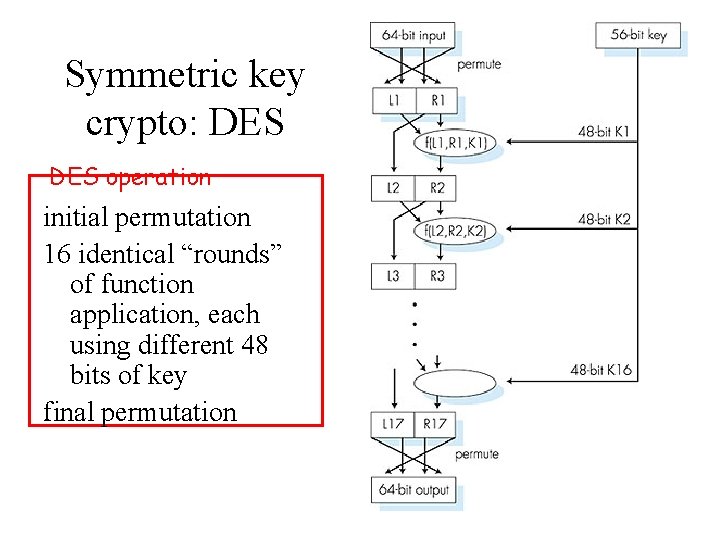
Symmetric key crypto: DES: Data Encryption Standard • US encryption standard [NIST 1993] • 56 -bit symmetric key, 64 -bit plaintext input • How secure is DES? – DES Challenge: 56 -bit-key-encrypted phrase (“Strong cryptography makes the world a safer place”) decrypted (brute force) in 4 months – no known “backdoor” decryption approach • making DES more secure: – use three keys sequentially (3 -DES) on each datum – use cipher-block chaining

Symmetric key crypto: DES operation initial permutation 16 identical “rounds” of function application, each using different 48 bits of key final permutation

Chapter 2 Symmetric Encryption Message Confidentiality

Outline • • • Symmetric Encryption Principles Symmetric Encryption Algorithms Cipher Block Modes of Operation Location of Encryption Devices Key Distribution

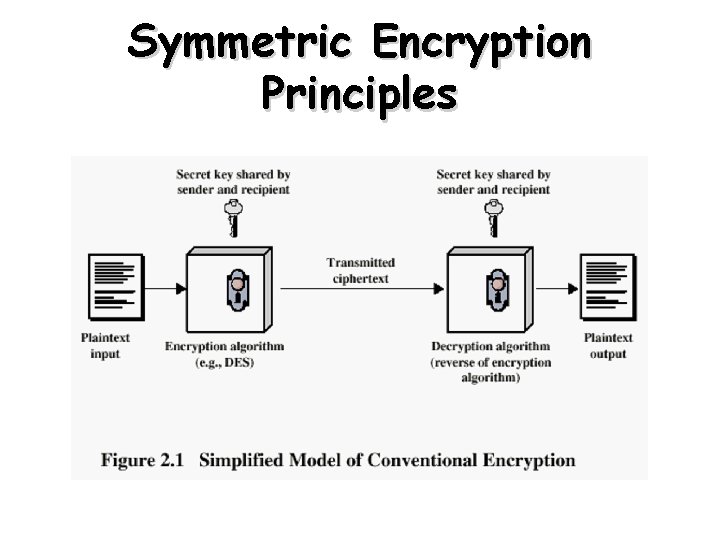
Symmetric Encryption Principles • An encryption scheme has five ingredients: – – – Plaintext Encryption algorithm Secret Key Ciphertext Decryption algorithm • Security depends on the secrecy of the key, not the secrecy of the algorithm

Symmetric Encryption Principles

Cryptography • Classified along three independent dimensions: – The type of operations used for transforming plaintext to ciphertext – The number of keys used • symmetric (single key) • asymmetric (two-keys, or public-key encryption) – The way in which the plaintext is processed

Cryptanalysis • Ciphertext only: – most difficult, – brute force approach of trying all possible keys, – the easiest to defend, • Ciphertext and plaintext pair: – known pattern in a file as well, – probable-word attack (e. g. placement of certain key words in the header of a file) – key can be deduced,

Cryptanalysis • Chosen plaintext: – analyst get the source system to insert into the system a message chosen by the analyst, – plaintext message chosen by cryptanalyst, together with its corresponding decrypted plaintext generated with the secret key,

Cryptanalysis • Chosen ciphertext: – purported ciphertext chosen by the analyst, together with its corresponding decrypted plaintext generated with the secret key

Computational security of an encryption • The cost of breaking the cipher exceeds the value of the encrypted information, • the time required to break the cipher exceeds the useful lifetime of the information

Average time required for exhaustive key search Key Size Number of Time required at (bits) Alternative Keys 106 Decryption/µs 32 232 = 4. 3 x 109 2. 15 milliseconds 56 256 = 7. 2 x 1016 10 hours 128 2128 = 3. 4 x 1038 5. 4 x 1018 years 168 2168 = 3. 7 x 1050 5. 9 x 1030 years

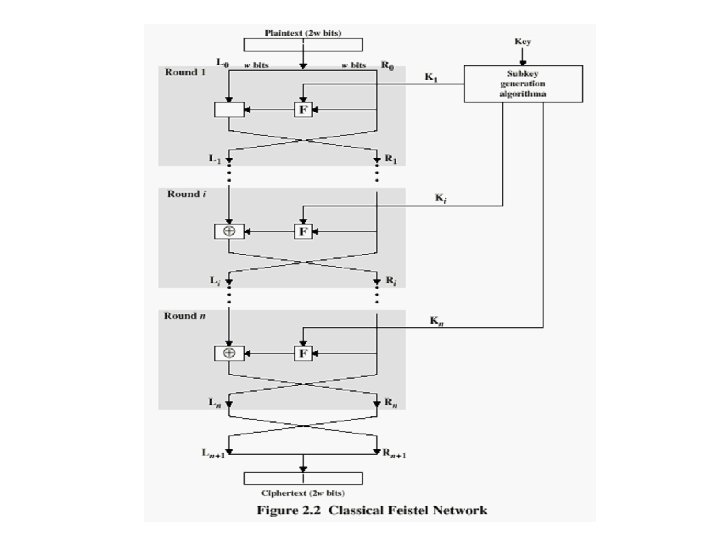
Feistel Cipher Structure • Virtually all conventional block encryption algorithms, including DES have a structure first described by Horst Feistel of IBM in 1973 • The realization of a Feistel Network depends on the choice of the following parameters and design features (see next slide):

Feistel Cipher Structure • Block size: larger block sizes mean greater security • Key Size: larger key size means greater security • Number of rounds: multiple rounds offer increasing security • Subkey generation algorithm: greater complexity will lead to greater difficulty of cryptanalysis. • Fast software encryption/decryption: the speed of execution of the algorithm becomes a concern

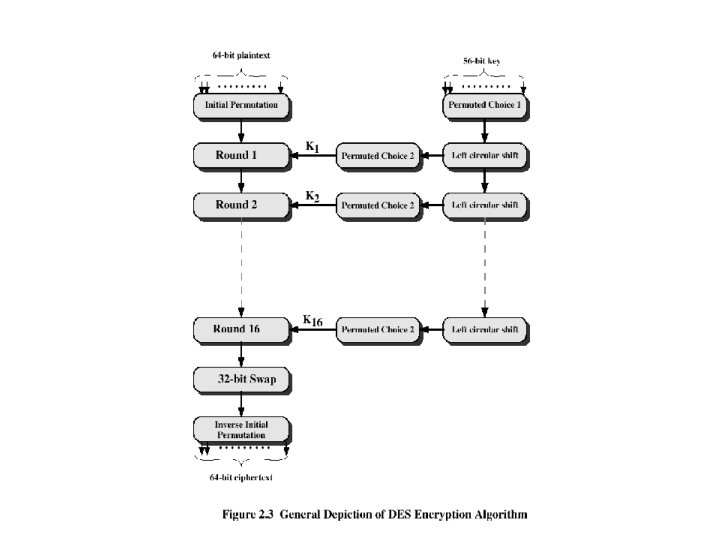
Symmetric Encryption Algorithms • Data Encryption Standard (DES) – The most widely used encryption scheme – The algorithm is referred to as the Data Encryption Algorithm (DEA) – DES is a block cipher – The plaintext is processed in 64 -bit blocks – The key is 56 -bits in length

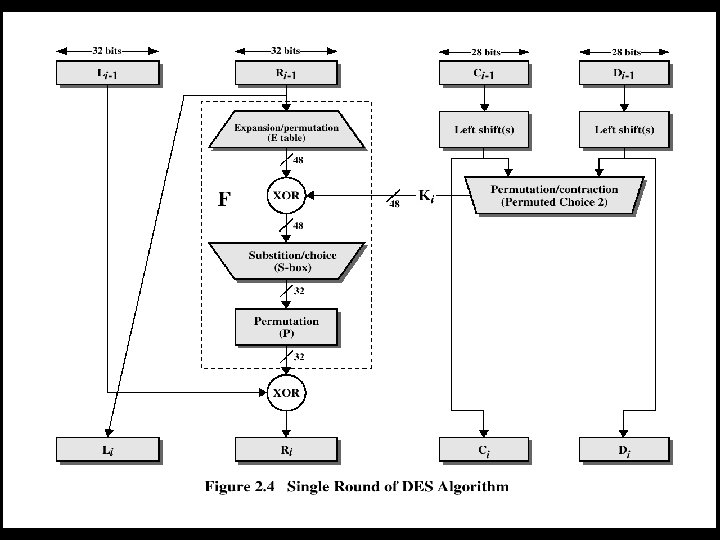
DES • The overall processing at each iteration: – Li = Ri-1 – Ri = Li-1 F(Ri-1, Ki) • Concerns about: – The algorithm and the key length (56 -bits)

Time to break a code (106 decryptions/µs)

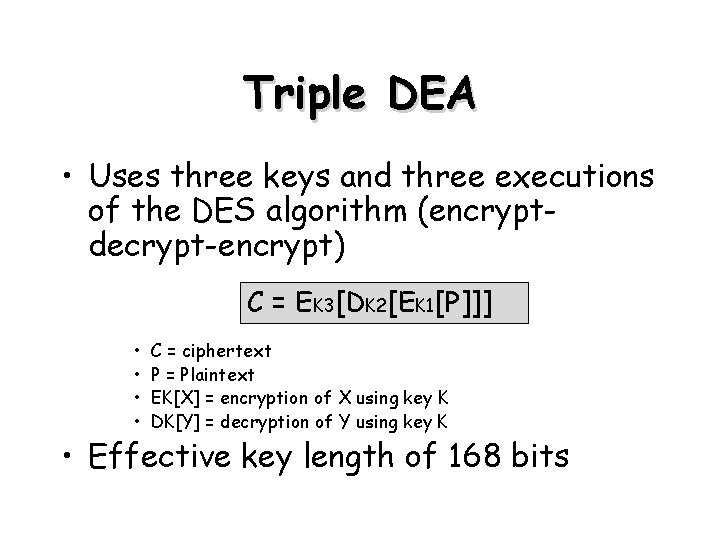
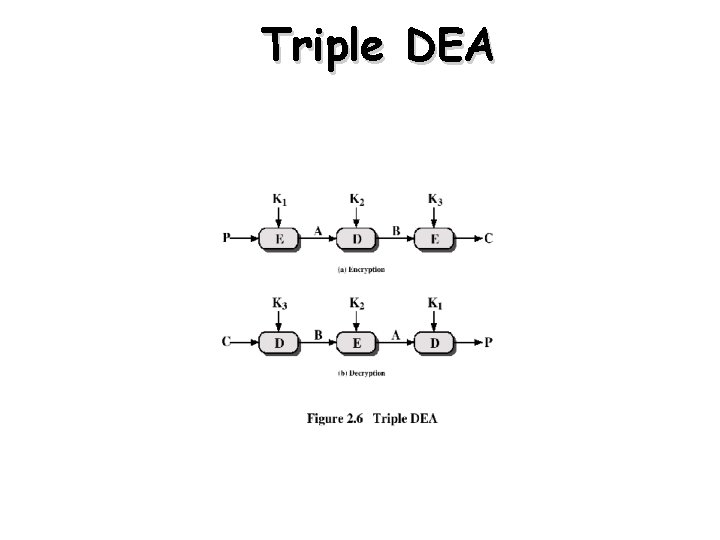
Triple DEA • Uses three keys and three executions of the DES algorithm (encryptdecrypt-encrypt) C = EK 3[DK 2[EK 1[P]]] • • C = ciphertext P = Plaintext EK[X] = encryption of X using key K DK[Y] = decryption of Y using key K • Effective key length of 168 bits

Triple DEA

AES: Advanced Encryption Standard • new (Nov. 2001) symmetric-key NIST standard, replacing DES • processes data in 128 bit blocks • 128, 192, or 256 bit keys • brute force decryption (try each key) taking 1 sec on DES, takes 149 trillion years for AES

Origins • clear a replacement for DES was needed – have theoretical attacks that can break it – have demonstrated exhaustive key search attacks • • • can use Triple-DES – but slow with small blocks US NIST issued call for ciphers in 1997 15 candidates accepted in Jun 98 5 were short-listed in Aug-99 Rijndael was selected as the AES in Oct-2000 issued as FIPS PUB 197 standard in Nov-2001

AES Requirements • • private key symmetric block cipher 128 -bit data, 128/192/256 -bit keys stronger & faster than Triple-DES active life of 20 -30 years (+ archival use) provide full specification & design details both C & Java implementations NIST have released all submissions & unclassified analyses

AES Evaluation Criteria • initial criteria: – security – effort to practically cryptanalyse – cost – computational – algorithm & implementation characteristics • final criteria – – general security software & hardware implementation ease implementation attacks flexibility (in en/decrypt, keying, other factors)

AES Shortlist • after testing and evaluation, shortlist in Aug-99: – – – MARS (IBM) - complex, fast, high security margin RC 6 (USA) - v. simple, v. fast, low security margin Rijndael (Belgium) - clean, fast, good security margin Serpent (Euro) - slow, clean, v. high security margin Twofish (USA) - complex, v. fast, high security margin • then subject to further analysis & comment • saw contrast between algorithms with – few complex rounds verses many simple rounds – which refined existing ciphers verses new proposals

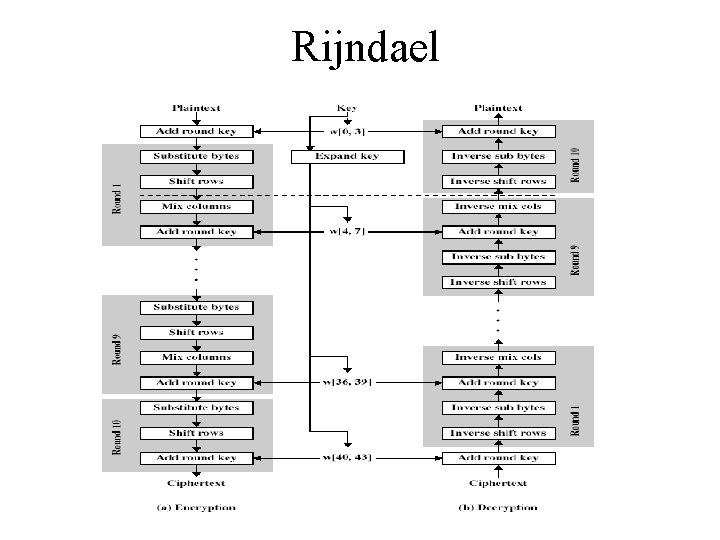
The AES Cipher - Rijndael • designed by Rijmen-Daemen in Belgium • has 128/192/256 bit keys, 128 bit data • an iterative rather than feistel cipher – treats data in 4 groups of 4 bytes – operates an entire block in every round • designed to be: – resistant against known attacks – speed and code compactness on many CPUs – design simplicity

Rijndael • processes data as 4 groups of 4 bytes (state) • has 9/11/13 rounds in which state undergoes: – – byte substitution (1 S-box used on every byte) shift rows (permute bytes between groups/columns) mix columns (subs using matrix multiply of groups) add round key (XOR state with key material) • initial XOR key material & incomplete last round • all operations can be combined into XOR and table lookups - hence very fast & efficient

Rijndael

Byte Substitution • a simple substitution of each byte • uses one table of 16 x 16 bytes containing a permutation of all 256 8 -bit values • each byte of state is replaced by byte in row (left 4 -bits) & column (right 4 -bits) – eg. byte {95} is replaced by row 9 col 5 byte – which is the value {2 A} • S-box is constructed using a defined transformation of the values in GF(28) • designed to be resistant to all known attacks

Shift Rows • a circular byte shift in each row – 1 st row is unchanged – 2 nd row does 1 byte circular shift to left – 3 rd row does 2 byte circular shift to left – 4 th row does 3 byte circular shift to left • decrypt does shifts to right • since state is processed by columns, this step permutes bytes between the columns

Mix Columns • each column is processed separately • each byte is replaced by a value dependent on all 4 bytes in the column • effectively a matrix multiplication in GF(28) using prime poly m(x) =x 8+x 4+x 3+x+1

Add Round Key • XOR state with 128 -bits of the round key • again processed by column (though effectively a series of byte operations) • inverse for decryption is identical since XOR is own inverse, just with correct round key • designed to be as simple as possible

AES Round

AES Key Expansion • takes 128 -bit (16 -byte) key and expands into array of 44/52/60 32 -bit words • start by copying key into first 4 words • then loop creating words that depend on values in previous & 4 places back – in 3 of 4 cases just XOR these together – every 4 th has S-box + rotate + XOR constant of previous before XOR together • designed to resist known attacks

AES Decryption • AES decryption is not identical to encryption since steps done in reverse • but can define an equivalent inverse cipher with steps as for encryption – but using inverses of each step – with a different key schedule • works since result is unchanged when – swap byte substitution & shift rows – swap mix columns & add (tweaked) round key

Implementation Aspects • can efficiently implement on 8 -bit CPU – byte substitution works on bytes using a table of 256 entries – shift rows is simple byte shifting – add round key works on byte XORs – mix columns requires matrix multiply in GF(28) which works on byte values, can be simplified to use a table lookup

Implementation Aspects • can efficiently implement on 32 -bit CPU – redefine steps to use 32 -bit words – can pre-compute 4 tables of 256 -words – then each column in each round can be computed using 4 table lookups + 4 XORs – at a cost of 16 Kb to store tables • designers believe this very efficient implementation was a key factor in its selection as the AES cipher

Other Symmetric Block Ciphers • International Data Encryption Algorithm (IDEA) – 128 -bit key – Used in PGP • Blowfish – Easy to implement – High execution speed – Runs in less than 5 K of memory

Other Symmetric Block Ciphers • RC 5 – Suitable for hardware and software – Fast, simple – Adaptable to processors of different word lengths – Variable number of rounds – Variable-length key – Low memory requirement – High security – Data-dependent rotations • Cast-128 – Key size from 40 to 128 bits – The round function differs from round to round