Cryptography Basics Objectives v v v Explain general

Cryptography Basics

Objectives v v v Explain general cryptography concepts Explain basic hashing concepts. Basic encryption concepts. Explain and implement protocols Explain core concepts of public key cryptography

Cryptography v Cryptography – science of encrypting information. v “scrambles” data so only authorized parties “unscramble” and read data using two methods can v. Can substitute – change one letter with a different letter v. Can transpose – scramble the order of letters, without actually changing one for another. v The best cryptosystems both substitute and transpose.

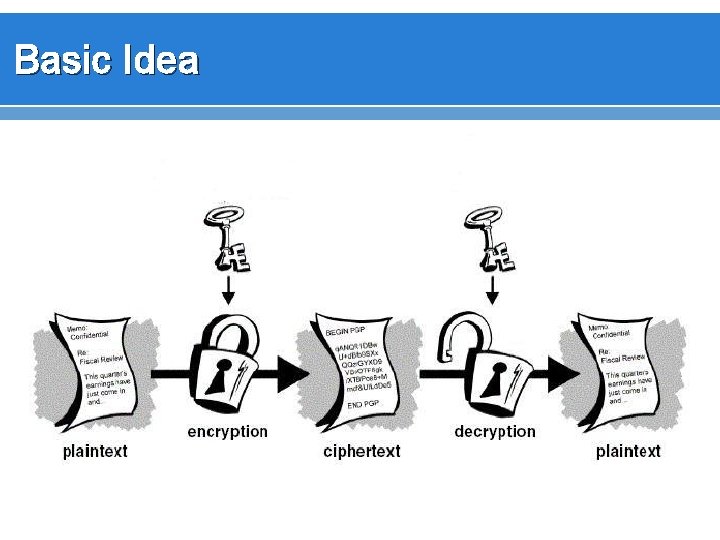
Basic Idea

Cryptographic Terminology v v v Cryptography - a method of storing and transmitting data in a form only intended for authorized parties to read or process. Cryptanalysis - science of studying, breaking, and reverse engineering algorithms and keys. Encryption – the method of transforming data (plaintext) into an unreadable format. Plain text – the format (usually readable) of data before being encrypted Cipher text – the “Scrambled” format of data after being encrypted

Cryptographic Terminology v v v Decryption – the method of turning cipher text back into plain text Encryption algorithm – a set or rules or procedures that dictates how to encrypt and decrypt data. Also called an encryption “cipher” Key – (crypto variable) a values used in the encryption process to encrypt and decrypt

Cryptographic Terminology v Key space – the range of possible values used to construct keys v example: vif a key can be 4 digits (0 -9) vkey space = 10, 000 (0000 – 9999) vif it can be 6 digits vkey space = 1, 000 (000, 000 – 999, 999) v v Key Clustering – Instance when two different keys generate the same cipher text from the same plaintext Work factor – estimated time and resources to break a cryptosystem

Cryptography History v Romans used a shift cipher called a “CEASAR” cipher. Shift Ciphers simply shift characters in an alphabet.

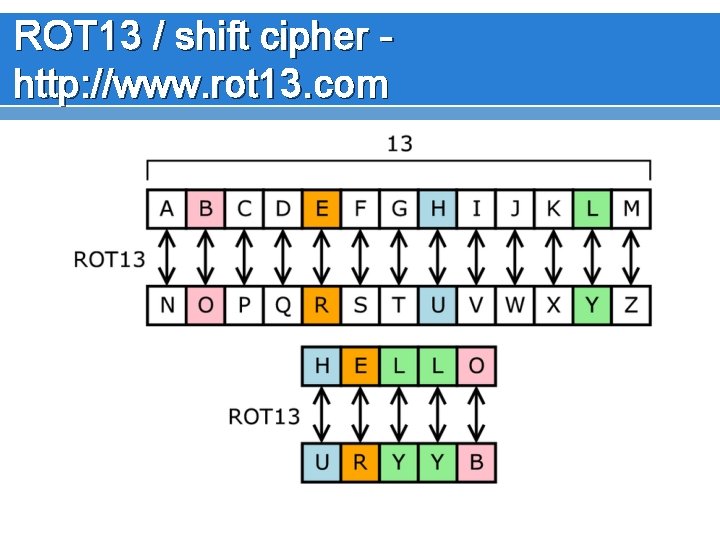
ROT 13 / shift cipher http: //www. rot 13. com

Transposition Cipher v Jumbles up the ordering of characters in a message. The Spartans of Greece used a form of this called the “Scytale” Cipher.

Transposition Cipher

Scytale

Steganography v v v Hiding one message in another “Meet the mini me that ate later. ” “Meet me later. ”

Vigenere Cipher v v v The Vigenère cipher is named for Blaise de Vigenère, although Giovan Battista Bellaso had invented the cipher earlier. Vigenère did invent a stronger autokey cipher. Vigenère cipher is a method of encrypting alphabetic text by using a series of different Caesar ciphers based on the letters of a keyword. It is a simple form of polyalphabetic substitution. This cipher is well known because while it is easy to understand implement, it often appears to beginners to be unbreakable.

Vigenere Table (tabula recta)

Vigenere Cipher v v v For example, suppose that the plaintext to be encrypted is: ATTACKATDAWN The person sending the message chooses a keyword and repeats it until it matches the length of the plaintext, for example, the keyword "LEMON": LEMONLE The first letter of the plaintext, A, is enciphered using the alphabet in row L, which is the first letter of the key. This is done by looking at the letter in row L and column A of the Vigenère square, namely L. The rest of the plaintext is enciphered in a similar fashion. Plaintext: ATTACKATDAWN Key: LEMONLE Ciphertext: LXFOPVEFRNHR

Encryption Modes – Block v Take the message and break it up into fixed sized blocks, encrypt each block using the given key.

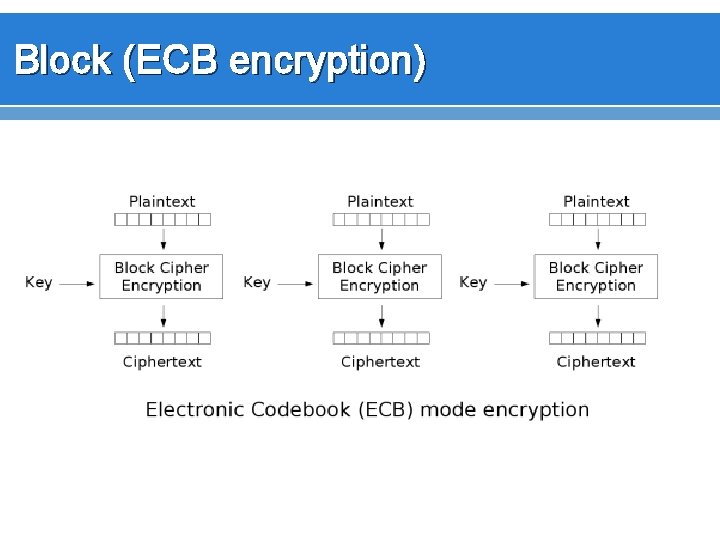
Block (ECB encryption)

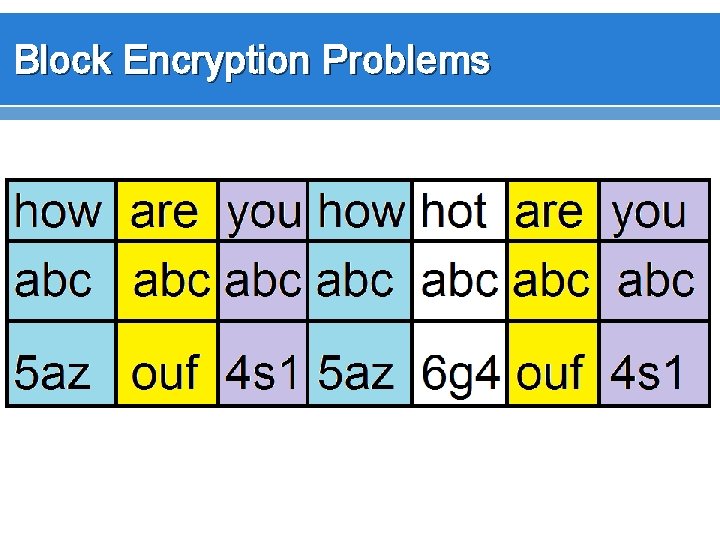
Block Encryption Problems

Solving Block Encryption Problems v v Often with block encryption, we include a value in addition to the key that changes for each block, so we don’t get repetitive cipher text blocks. This is called Cipher Block Chaining (see next slide) Initialization Vectors are used with the first block in CBC

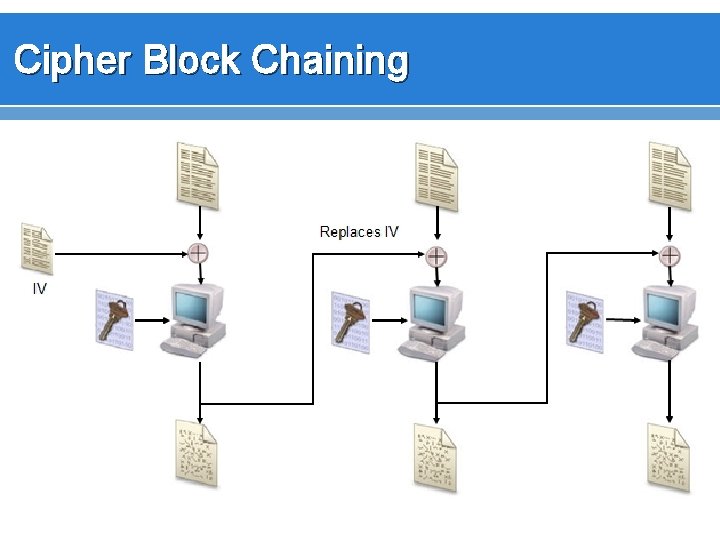
Cipher Block Chaining

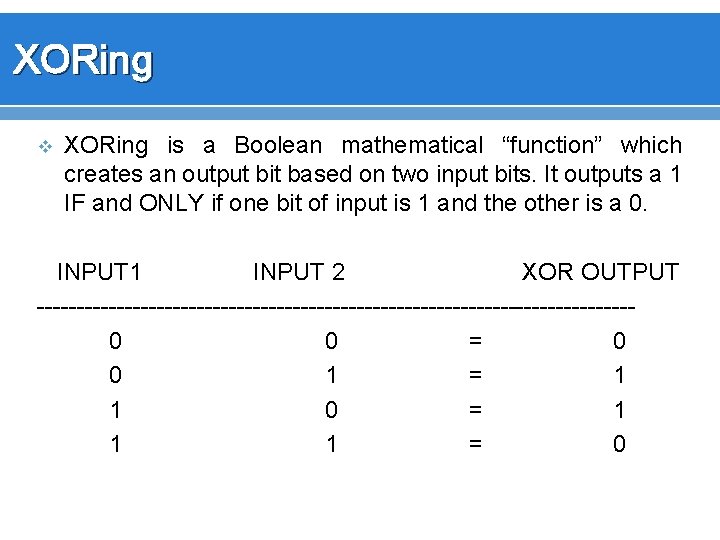
XORing v XORing is a Boolean mathematical “function” which creates an output bit based on two input bits. It outputs a 1 IF and ONLY if one bit of input is 1 and the other is a 0. INPUT 1 INPUT 2 XOR OUTPUT -------------------------------------0 0 = 0 0 1 = 1 1 0 = 1 1 1 = 0

Stream Encryption v v The “key” is used as a key stream generator, which creates a series of bits each are is mathematically combined with the bit stream of plaintext to produce cipher text. This is done for small pieces of information, or information not in blocks. Keyboard input Morse code Any input that arrives one bit or byte at a time

Stream Encryption Plain Text Bit 0 1 1 0 1 XOR v Cipher text = 0 Keystream Bit 1 1 0 1 1 = Output Bit 0

Stream Encryption Plain Text Bit 0 1 1 0 v Keystream Bit XOR Cipher text = 0 1 1 1 0 1 Output Bit = 1

Stream Encryption Plain Text Bit 0 1 1 Keystream Bit XOR Cipher text = 0 1 1 0 Output Bit = 1

Stream Encryption Plain Text Bit 0 1 Keystream Bit XOR Cipher text = 0 1 1 Output Bit = 0

Stream Encryption Plain Text Bit 0 Keystream Bit XOR Cipher text = 0 1 1 Output Bit = 1

One Time Pad v v v 1011 – plain text 0101 – pad ------ XOR 1110 – cipher text In a one time pad you use a different key/pad each time you send a message

One Time Pad v v v A “perfect cryptosystem” Unbreakable if implemented properly The key is a series of bits (0 and 1) The plain text is converted to bits The message is XORed with the pad/key to generated the cipher text (more)

One Time Pad considerations v v v The pad must be used only one time The pad must be shared by both sides. The pad must be as long as the message The pad must be securely distributed The pad must be used up of truly random values

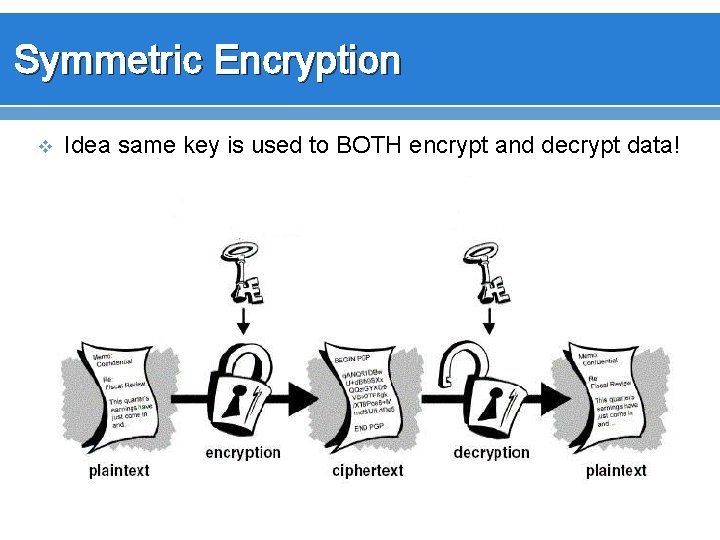
Symmetric Encryption v Idea same key is used to BOTH encrypt and decrypt data!

Symmetric Encryption v Called Symmetric or “Private Key encryption” v Must securely distribute keys to both parties. v v Chicken in the egg situation with networks Anyone with the key can either encrypt or decrypt Very Fast to encrypt or decrypt Key Management is the big issue

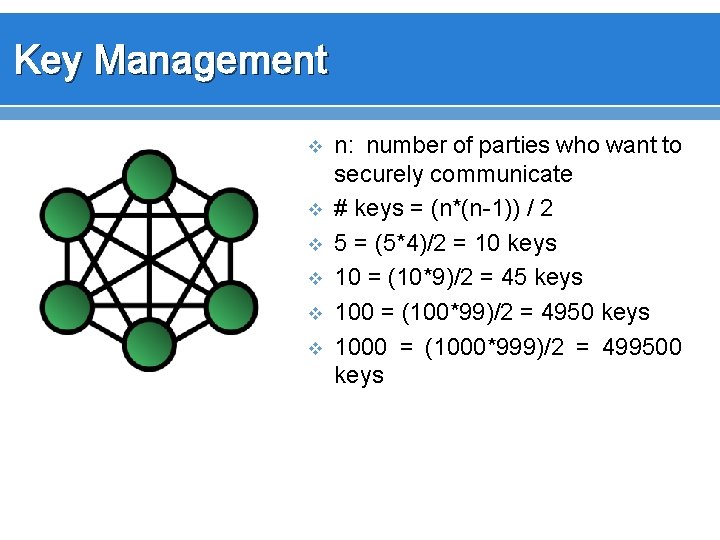
Key Management v v v n: number of parties who want to securely communicate # keys = (n*(n-1)) / 2 5 = (5*4)/2 = 10 keys 10 = (10*9)/2 = 45 keys 100 = (100*99)/2 = 4950 keys 1000 = (1000*999)/2 = 499500 keys

Symmetric Algorithms – DES v v v v Data Encryption Standard Developed from at NIST request for an encryption standard Chosen algorithm was called “Lucifer” from IBM Block Cipher Fixed sized blocks of 64 bits Key size 64 bits, effective size is 56 bits 16 rounds of substitution and transposition DES is no longer considered strong enough, can be broken easily with distributed computing.

Triple DES v v v Nothing but DES 3 times 3 DES – EEE 3 3 DES – EDE 3 3 DES – EEE 2 3 DES – EDE 2 Since it’s 3 x DES, 48 rounds of substitution and transposition.

AES v v v Developed as a replacement to DES Actual algorithm is called “Rinjdael” Block cipher 128 bit blocks Key sizes of 128, 192, 256 Rounds depend on key size v 9: for 128 keys v 11: for 192 keys v 13: for 256 bit keys

RC 5 v v Block cipher Block size 32, 64, 128 Key Size up to 2048 bits Rounds up to 255, minimum of 12 recommended

RC 6 v v Block cipher based on RC 5 Same attributes as RC 5 Developed to be a AES candidate Faster that RC 5

RC 4 v v Stream cipher – what was that again? Was proprietary, but released on Internet in 1994, “ARC 4” is the “open version of RC 4” Key length 8 – 2048 bits Used in SSL and WEP communication

Blowfish v v v Block cipher 64 bit blocks Keys 32 - 448 bits 16 rounds is the “full version” Free algorithm

IDEA v v v v International Data Encryption Algorithm Proposed AES candidate Block cipher 64 bit blocks 128 bit keys Not free, Patent expires soon though Used in PGP

Symmetric v v v That’s Symmetric Encryption Understand the concept (shared keys) Understand it’s strengths (fast for bulk encryption and decryption) Understand it’s weaknesses (key management, nonrepudiation) Understand the different algorithm “properties” on the slides.

Enter Non-Repudiation v v Non-Repudiation – being able to definitively prove someone said or wrote something. Proves they actually sent a message Proves the message was not altered How do we provide non-repudiation? We’ll see soon after we talk about hashes, and asymmetric encryption.

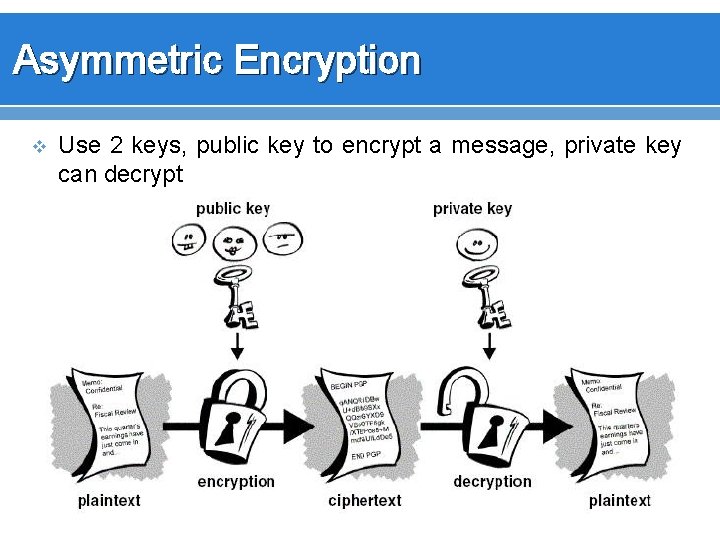
Asymmetric Encryption v Use 2 keys, public key to encrypt a message, private key can decrypt

Asymmetric Encryption v v v v Called Public key encryption Requires 2 related keys Public key – given to anyone Private key – kept secret Public key is used to encrypt message Private key is used to decrypt message Private key is used to sign messages Public key is used to validate signed messages

Asymmetric Encryption v v v v Key exchange is simple! Asymmetric Encryption is SLOW, not suitable for encrypting large amounts of data What is a problem with Asymmetric Encryption and key exchange? (Mi. M) Can be used to “digitally sign” a message (in a few slides) Provides integrity Provides non-repudiation Can anyone see a use to Asymmetric encryption already? * (very important)

Diffie-Hellman v v The original Asymmetric algorithm Used with SSL, VPNs, ssh Used ONLY for key exchange Generates session keys for secure SYMETRIC encryption communications

Asymmetric Algorithms – RSA v v Can be 100 times slower than DES Can be used for encryption, key exchange and digital signatures Security based on difficulty of factoring large numbers. Was patented, has expired

El-Gamal v v v Encryption or digital signatures Free Can be used for encryption, key exchange and digital signatures Slow Based on / extended Diffie-Hellman

ECC - Elliptic Curve Cryptography v v v Encryption, key exchange or digital signatures Security based on analyzing elliptic curves in finite fields Does not require much computing overhead as such used in devices with low resources (PDAs, Cell phones etc)*

Asymmetric Overview v v v Uses 2 keys, one for encryption, one for decryption This mitigates the key management, key distribution problem (kind of…) Is VERY slow (orders of magnitude slower) Can provide integrity and proof of sender (non-repudiation) Often used in a hybrid system (along with private key encryption) v Encrypt symmetric keys using asymmetric algorithms v Actually do large scale encryption with these asymmetric keys!

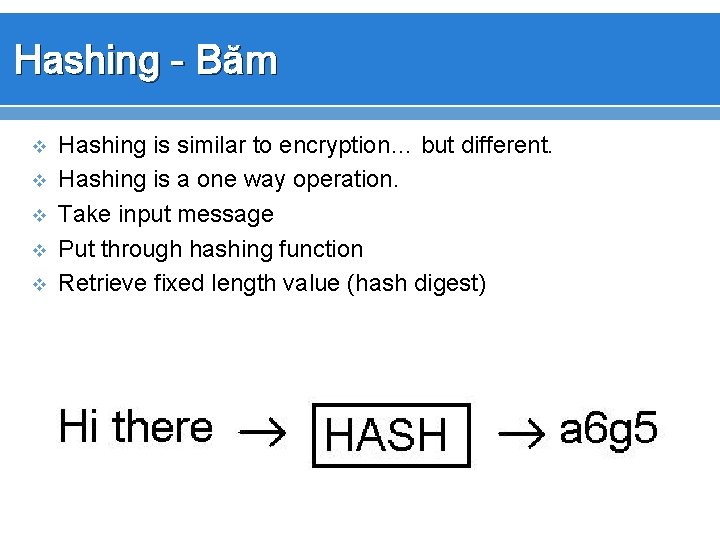
Hashing - Băm v v v Hashing is similar to encryption… but different. Hashing is a one way operation. Take input message Put through hashing function Retrieve fixed length value (hash digest)

Hashing v Try for yourself at http: //www. fileformat. info/tool/hash. htm

Hashes v v Once hashed, no way to get back the original message Hash digests are fixed, so multiple messages theoretically could produce the same hash digest (collision)

Hashes v v Hashing can provide integrity (assuming no Mi. M (next slide)) Hashes can be combined with a private key to provide protection against Mi. M attacks (visualization in a few slides next slide) The more bits in the digest, generally the more secure (less change for collision…generally) One Example of a hash that you are probably familiar with is called a “CRC”

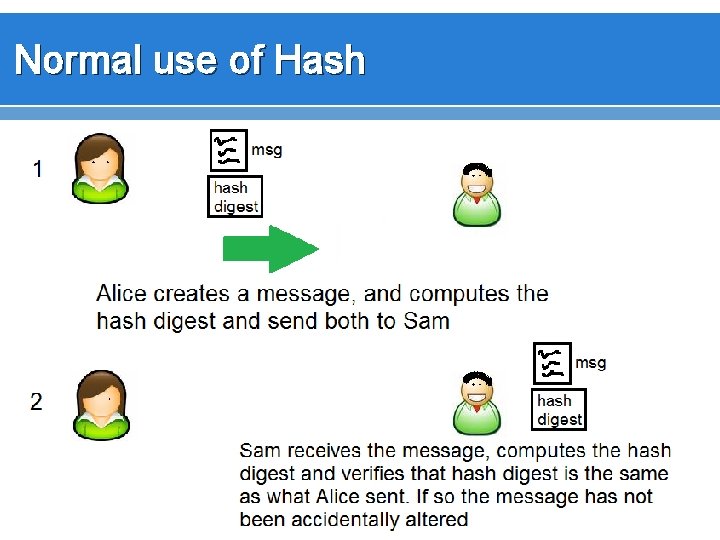
Normal use of Hash

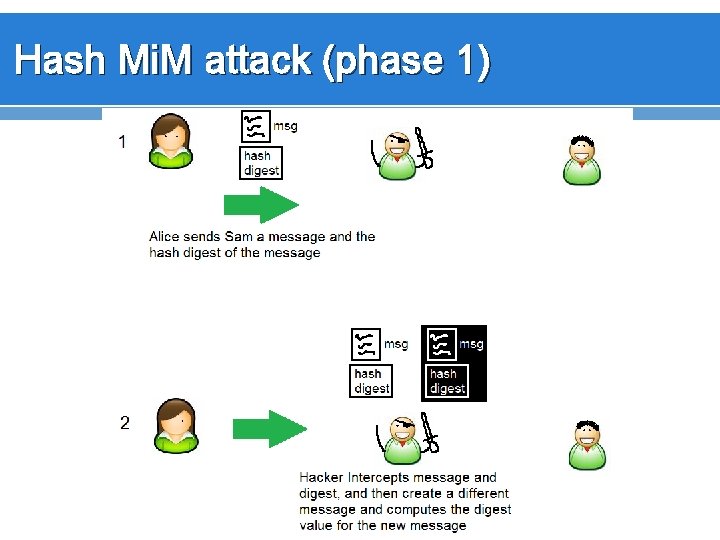
Hash Mi. M attack (phase 1)

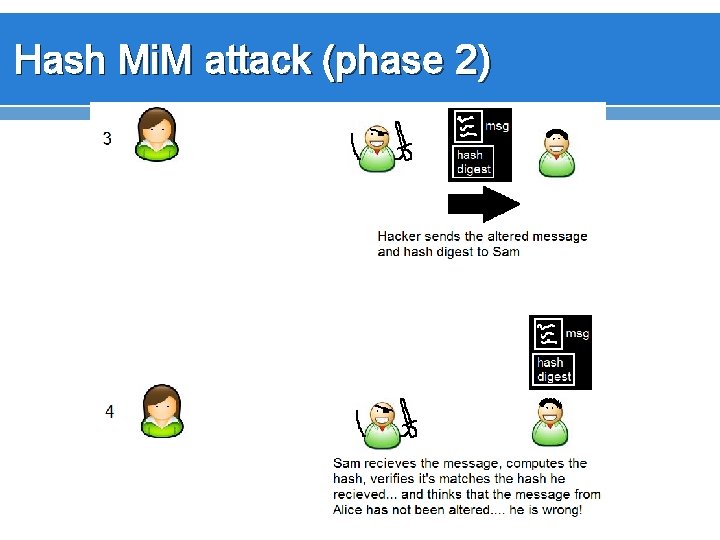
Hash Mi. M attack (phase 2)

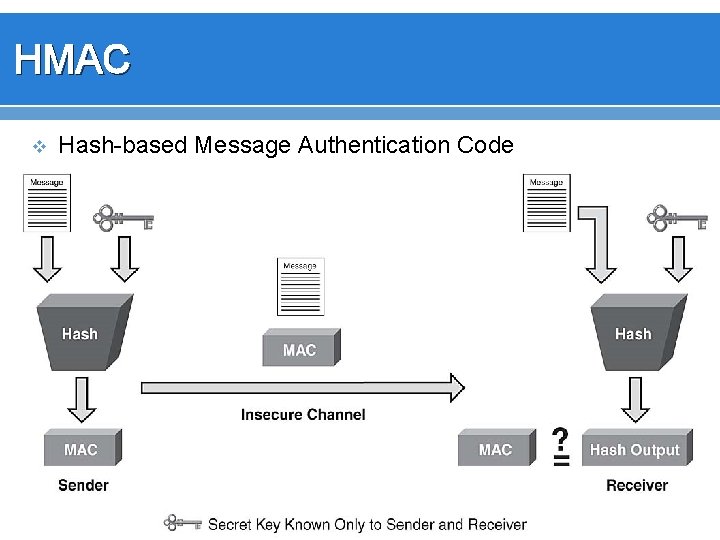
HMAC v Hash-based Message Authentication Code

HMAC function hmac (key, message) if (length(key) > blocksize) then key = hash(key) // keys longer than blocksize are shortened end if if (length(key) < blocksize) then key = key ∥ zeroes(blocksize - length(key)) // keys shorter than blocksize are zero-padded end if o_key_pad = [0 x 5 c * blocksize] ⊕ key // Where blocksize is that of the underlying hash function i_key_pad = [0 x 36 * blocksize] ⊕ key // Where ⊕ is exclusive or (XOR) return hash(o_key_pad ∥ hash(i_key_pad ∥ message)) // Where ∥ is concatenation end function

Hash algorithms – SHA v v v Secure Hash Algorithm Designed/Published by NIST and NSA Designed for use in the DSS Modeled after MD 4 SHA-1 (SHA-160) – 160 bit digest v 512 bit blocks v SHA-256 – 256 bit digest v 512 bit blocks v SHA-384 – 384 bit digest v 1024 bit blocks v SHA-512 – 512 bit digest v 1024 bit blocks

MD 2 v v Developed by Ronald Rivest (of RC and RSA fame) Optimized to run on 8 bit computers 128 bit digest 128 bit blocks

MD 4 v v v Optimized for 32 bit computers 128 bit digest Collisions can be found in under 1 minute on a PC ; (

MD 5 v v v v Similar to MD 4, but more secure Slower and more secure 128 bit digest 512 bit blocks Was part of the NTLM authentication protocol Collisions in 8 hours on a PC Moving away from, to SHA

Hash overview v Know what a hash is v Concept v Fixed length digest v What is a hash used for v Know what a collision is v Know it’s susceptible to Mi. M v Know what HMAC is, and what it tries to accomplish v v Be familiar with MDx, and SHA-x Understand that SHA is considered the best algorithm

Digital Signatures

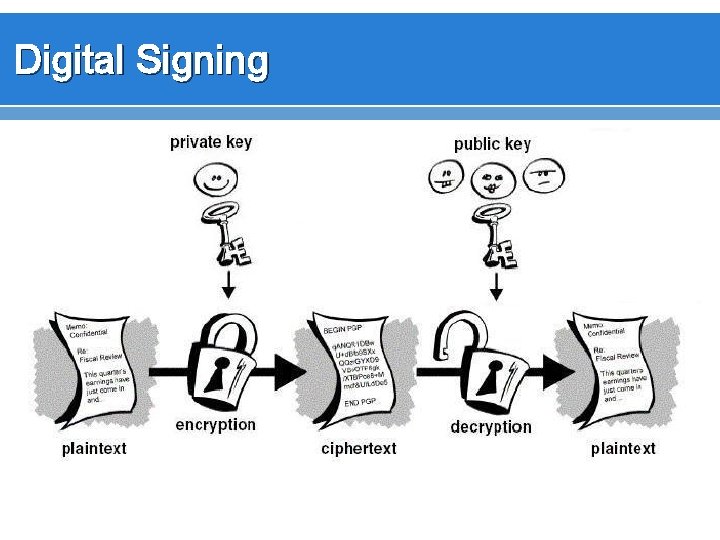
Digital Signing

Digital Signing v Generally when I digital sign something. . I don’t encrypt the whole message. Instead v Run message through hash algorithm, generated message digest v Sign the “message digest” v Send both the original message and the encrypted message digest

Digital Signing v Provides v Integrity v Non repudiation v NOT confidentiality

Digital Signing