Cryptography and Network Security Principles and Practice Eighth

Cryptography and Network Security: Principles and Practice Eighth Edition Chapter 6 Advanced Encryption Standard Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Learning Objectives • Present an overview of the general structure of Advanced Encryption Standard (AES). • Understand the four transformations used in AES. • Explain the AES key expansion algorithm. • Understand the use of polynomials with coefficients in GF(28). Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Finite Field Arithmetic (1 of 2) • In the Advanced Encryption Standard (A E S) all operations are performed on 8 -bit bytes • The arithmetic operations of addition, multiplication, and division are performed over the finite field G F(28) • A field is a set in which we can do addition, subtraction, multiplication, and division without leaving the set • Division is defined with the following rule: – a /b = a (b− 1 ) • An example of a finite field (one with a finite number of elements) is the set Zp consisting of all the integers {0, 1, . . , p − 1}, where p is a prime number and in which arithmetic is carried out modulo p Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Finite Field Arithmetic (2 of 2) • If one of the operations used in the algorithm is division, then we need to work in arithmetic defined over a field – Division requires that each nonzero element have a multiplicative inverse • For convenience and for implementation efficiency we would like to work with integers that fit exactly into a given number of bits with no wasted bit patterns – Integers in the range 0 through 2 n – 1, which fit into an n-bit word • The set of such integers, Z 2 n, using modular arithmetic, is not a field – For example, the integer 2 has no multiplicative inverse in Z 2 n, that is, there is no integer b, such that 2 b mod 2 n = 1 • A finite field containing 2 n elements is referred to as G F(2 n) – Every polynomial in G F(2 n) can be represented by an n-bit number Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

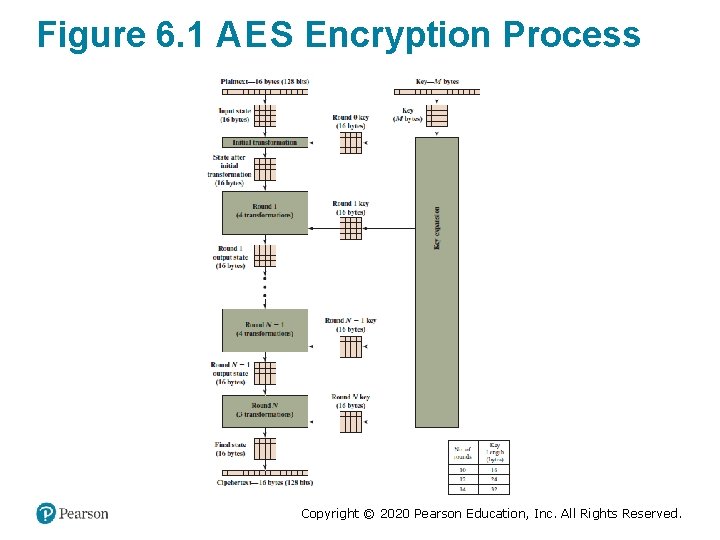
Figure 6. 1 A E S Encryption Process Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

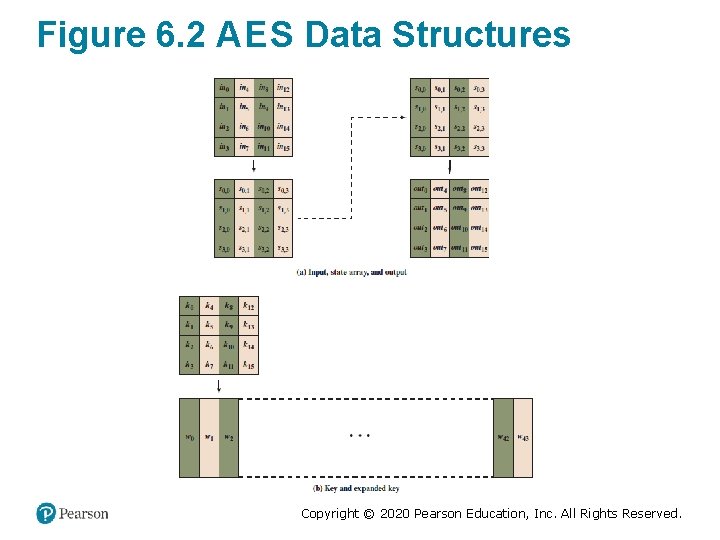
Figure 6. 2 A E S Data Structures Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

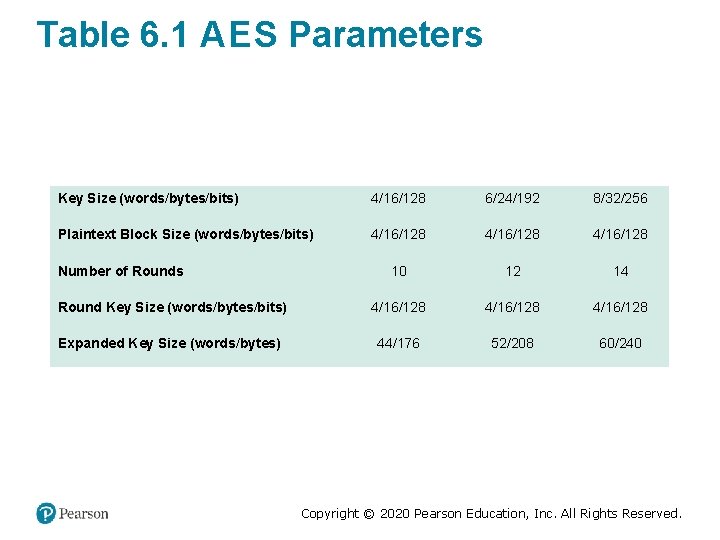
Table 6. 1 A E S Parameters Key Size (words/bytes/bits) 4/16/128 6/24/192 8/32/256 Plaintext Block Size (words/bytes/bits) 4/16/128 10 12 14 Round Key Size (words/bytes/bits) 4/16/128 Expanded Key Size (words/bytes) 44/176 52/208 60/240 Number of Rounds Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

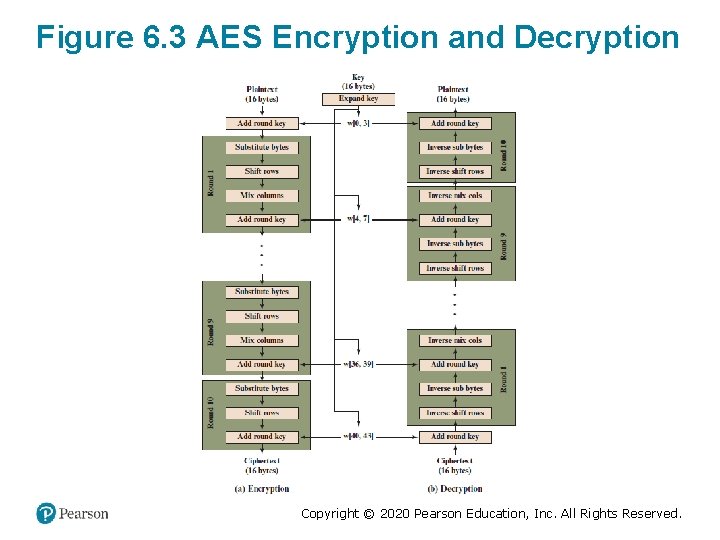
Figure 6. 3 AES Encryption and Decryption Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

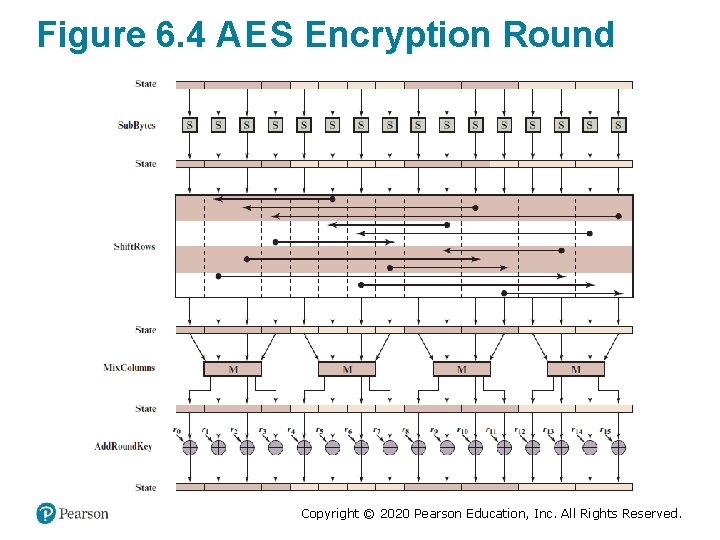
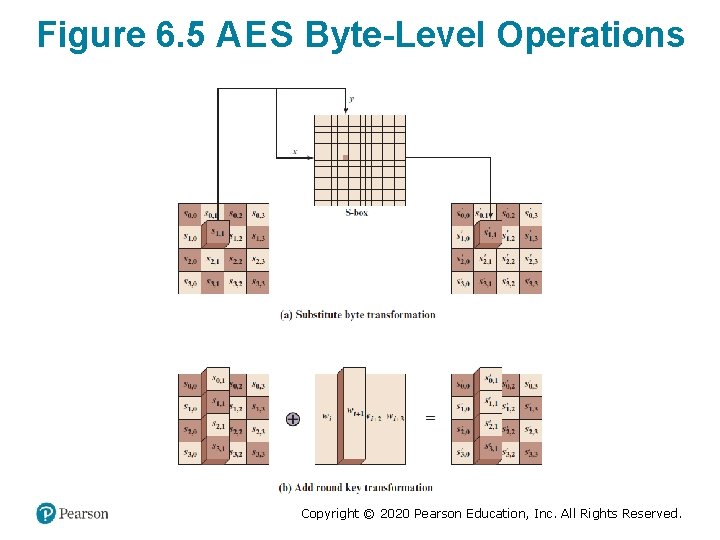
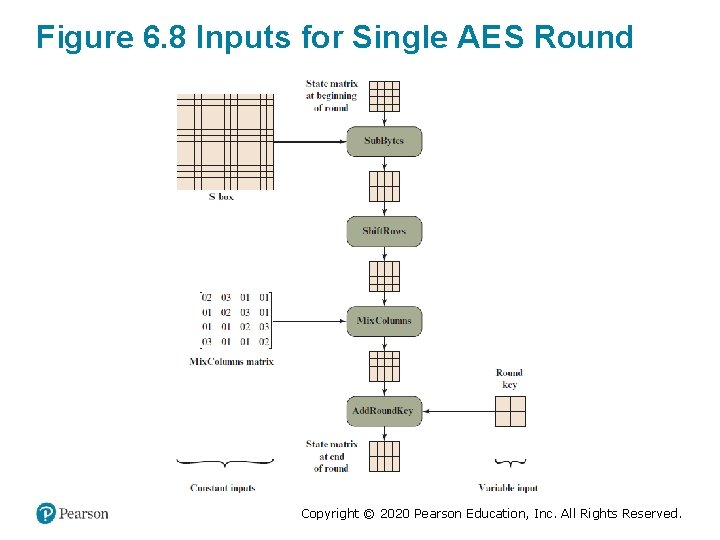
Detailed Structure (1 of 2) • Processes the entire data block as a single matrix during each round using substitutions and permutation • The key that is provided as input is expanded into an array of forty-four 32 -bit words, w[i] • Four different stages are used: – Substitute bytes – uses an S-box to perform a byte-bybyte substitution of the block – Shift. Rows – a simple permutation – Mix. Columns – a substitution that makes use of arithmetic over GF(28) – Add. Round. Key – a simple bitwise X O R of the current block with a portion of the expanded key Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Detailed Structure (2 of 2) • The cipher begins and ends with an Add. Round. Key stage • Can view the cipher as alternating operations of X O R encryption (Add. Round. Key) of a block, followed by scrambling of the block (the other three stages), followed by X O R encryption, and so on • Each stage is easily reversible • The decryption algorithm makes use of the expanded key in reverse order, however the decryption algorithm is not identical to the encryption algorithm • State is the same for both encryption and decryption • Final round of both encryption and decryption consists of only three stages Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Figure 6. 4 A E S Encryption Round Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Figure 6. 5 A E S Byte-Level Operations Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

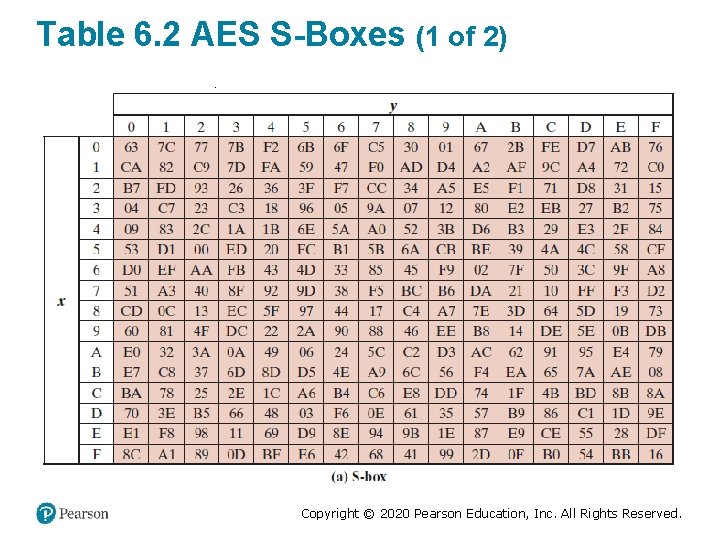
Table 6. 2 AES S-Boxes (1 of 2) Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

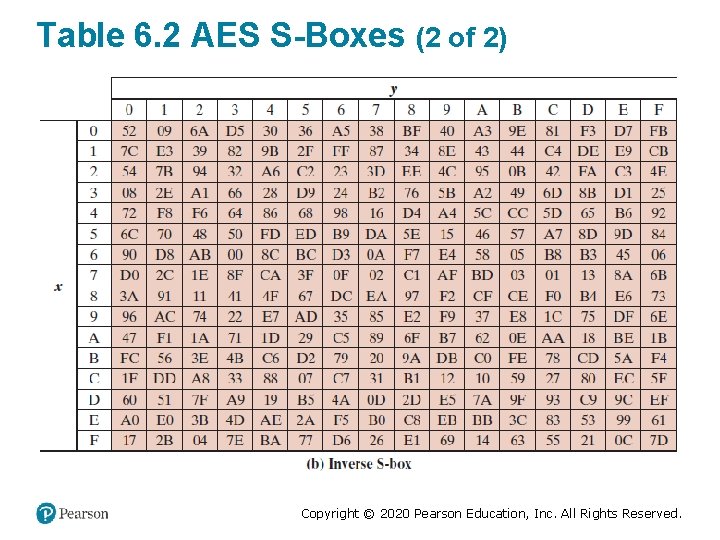
Table 6. 2 AES S-Boxes (2 of 2) Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

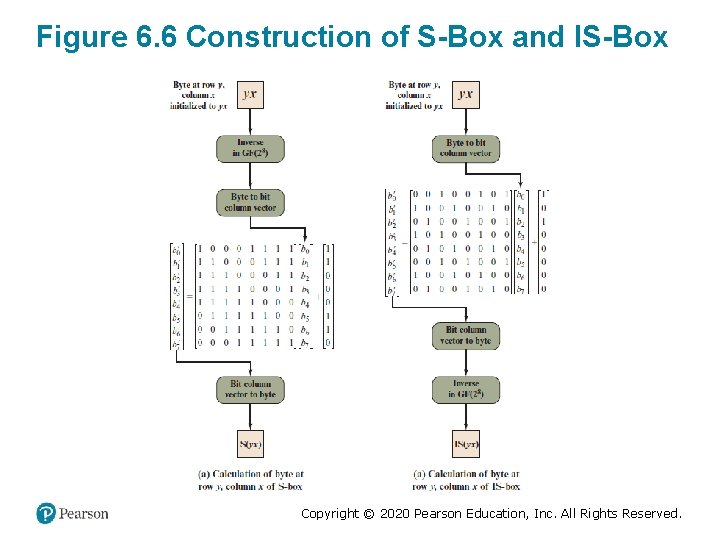
Figure 6. 6 Construction of S-Box and IS-Box Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

S-Box Rationale • The S-box is designed to be resistant to known cryptanalytic attacks • The Rijndael developers sought a design that has a low correlation between input bits and output bits and the property that the output is not a linear mathematical function of the input • The nonlinearity is due to the use of the multiplicative inverse Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

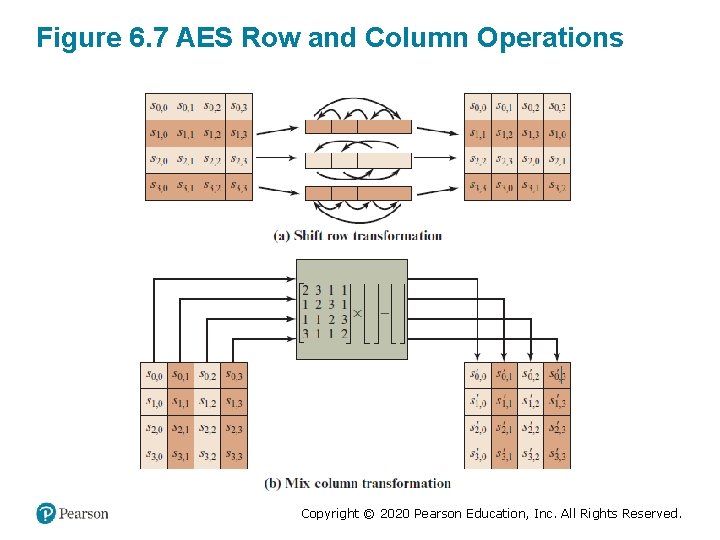
Figure 6. 7 AES Row and Column Operations Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Shift Row Rationale • More substantial than it may first appear • The State, as well as the cipher input and output, is treated as an array of four 4 -byte columns • On encryption, the first 4 bytes of the plaintext are copied to the first column of State, and so on • The round key is applied to State column by column – Thus, a row shift moves an individual byte from one column to another, which is a linear distance of a multiple of 4 bytes • Transformation ensures that the 4 bytes of one column are spread out to four different columns Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Mix Columns Rationale • Coefficients of a matrix based on a linear code with maximal distance between code words ensures a good mixing among the bytes of each column • The mix column transformation combined with the shift row transformation ensures that after a few rounds all output bits depend on all input bits Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Add. Round. Key Transformation • The 128 bits of State are • Rationale: bitwise XORed with the 128 – Is as simple as possible bits of the round key and affects every bit of • Operation is viewed as a State columnwise operation – The complexity of the between the 4 bytes of a round key expansion State column and one word plus the complexity of of the round key the other stages of AE S – Can also be viewed as ensure security a byte-level operation Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Figure 6. 8 Inputs for Single AES Round Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

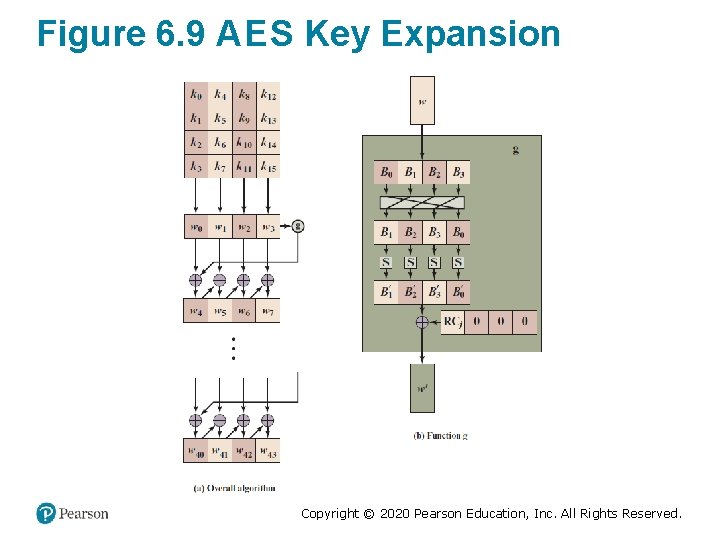
A E S Key Expansion • Takes as input a four-word (16 byte) key and produces a linear array of 44 words (176) bytes – This is sufficient to provide a four-word round key for the initial Add. Round. Key stage and each of the 10 rounds of the cipher • Key is copied into the first four words of the expanded key – The remainder of the expanded key is filled in four words at a time • Each added word w[i] depends on the immediately preceding word, w[i – 1], and the word four positions back, w[i – 4] – In three out of four cases a simple XOR is used – For a word whose position in the w array is a multiple of 4, a more complex function is used Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Figure 6. 9 A E S Key Expansion Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Key Expansion Rationale (1 of 2) • The Rijndael developers designed the expansion key algorithm to be resistant to known cryptanalytic attacks • Inclusion of a round-dependent round constant eliminates the symmetry between the ways in which round keys are generated in different rounds Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Key Expansion Rationale (2 of 2) • The specific criteria that were used are: – Knowledge of a part of the cipher key or round key does not enable calculation of many other round-key bits – An invertible transformation – Speed on a wide range of processors – Usage of round constants to eliminate symmetries – Diffusion of cipher key differences into the round keys – Enough nonlinearity to prohibit the full determination of round key differences from cipher key differences only – Simplicity of description Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

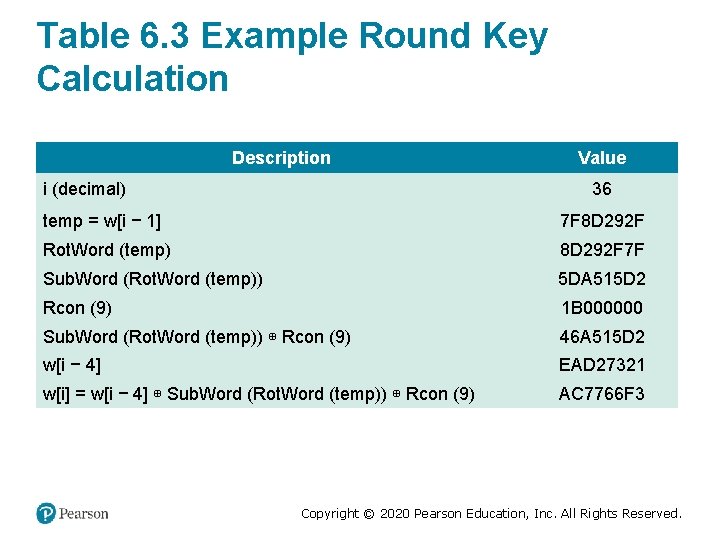
Table 6. 3 Example Round Key Calculation Description i (decimal) Value 36 temp = w[i − 1] 7 F 8 D 292 F Rot. Word (temp) 8 D 292 F 7 F Sub. Word (Rot. Word (temp)) 5 DA 515 D 2 Rcon (9) 1 B 000000 Sub. Word (Rot. Word (temp)) ⊕ Rcon (9) 46 A 515 D 2 w[i − 4] EAD 27321 w[i] = w[i − 4] ⊕ Sub. Word (Rot. Word (temp)) ⊕ Rcon (9) AC 7766 F 3 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Table 6. 4 Key Expansion for A E S Example (1 of 3) Key Words Auxiliary Function w 0 = 0 f 15 71 c 9 w 1 = 47 d 9 e 8 59 w 2 = 0 c b 7 ad d 6 w 3 = af 7 f 67 98 Rot. Word (w 3) = 7 f 67 98 af = x 1 Sub. Word (x 1) = d 2 85 46 79 = y 1 Rcon (1) = 01 00 00 00 y 1 ⊕ Rcon (1) = d 3 85 46 79 = z 1 w 4 = w 0 ⊕ z 1 = dc 90 37 b 0 w 5 = w 4 ⊕ w 1 = 9 b 49 df e 9 w 6 = w 5 ⊕ w 2 = 97 fe 72 3 f w 7 = w 6 ⊕ w 3 = 38 81 15 a 7 Rot. Word (w 7) = 81 15 a 7 38 = x 2 Sub. Word (x 2) = 0 c 59 5 c 07 = y 2 Rcon (2) = 02 00 00 00 y 2 ⊕ Rcon (2) = 0 e 59 5 c 07 = z 2 w 8 = w 4 ⊕ z 2 = d 2 c 9 6 b b 7 w 9 = w 8 ⊕ w 5 = 49 80 b 4 5 e w 10 = w 9 ⊕ w 6 = de 7 e c 6 61 w 11 = w 10 ⊕ w 7 = e 6 ff d 3 c 6 Rot. Word (w 11) = ff d 3 c 6 e 6 = x 3 Sub. Word (x 3) = 16 66 b 4 83 = y 3 Rcon (3) = 04 00 00 00 y 3 ⊕ Rcon (3) = 12 66 b 4 8 e = z 3 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Table 6. 4 Key Expansion for A E S Example (2 of 3) Key Words Auxiliary Function w 12 = w 8 ⊕ z 3 = c 0 af df 39 w 13 = w 12 ⊕ w 9 = 89 2 f 6 b 67 w 14 = w 13 ⊕ w 10 = 57 51 ad 06 w 15 = w 14 ⊕ w 11 = b 1 ae 7 e c 0 Rot. Word (w 15) = ae 7 e c 0 b 1 = x 4 Sub. Word (x 4) = e 4 f 3 ba c 8 = y 4 Rcon (4) = 08 00 00 00 y 4 ⊕ Rcon (4) = ec f 3 ba c 8 = 4 w 16 = w 12 ⊕ z 4 = 2 c 5 c 65 f 1 w 17 = w 16 ⊕ w 13 = a 5 73 0 e 96 w 18 = w 17 ⊕ w 14 = f 2 22 a 3 90 w 19 = w 18 ⊕ w 15 = 43 8 c dd 50 Rot. Word (w 19) = 8 c dd 50 43 = x 5 Sub. Word (x 5) = 64 c 1 53 1 a = y 5 Rcon(5) = 10 00 00 00 y 5 ⊕ Rcon (5) = 74 c 1 53 1 a = z 5 w 20 = w 16 ⊕ z 5 = 58 9 d 36 eb w 21 = w 20 ⊕ w 17 = fd ee 38 7 d w 22 = w 21 ⊕ w 18 = 0 f cc 9 b ed w 23 = w 22 ⊕ w 19 = 4 c 40 46 bd Rot. Word (w 23) = 40 46 bd 4 c = x 6 Sub. Word (x 6) = 09 5 a 7 a 29 = y 6 Rcon(6) = 20 00 00 00 y 6 ⊕ Rcon(6) = 29 5 a 7 a 29 = z 6 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

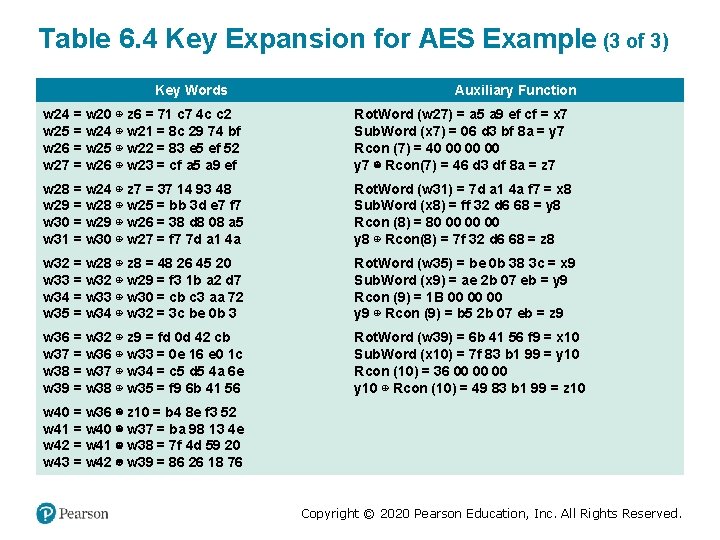
Table 6. 4 Key Expansion for AES Example (3 of 3) Key Words Auxiliary Function w 24 = w 20 ⊕ z 6 = 71 c 7 4 c c 2 w 25 = w 24 ⊕ w 21 = 8 c 29 74 bf w 26 = w 25 ⊕ w 22 = 83 e 5 ef 52 w 27 = w 26 ⊕ w 23 = cf a 5 a 9 ef Rot. Word (w 27) = a 5 a 9 ef cf = x 7 Sub. Word (x 7) = 06 d 3 bf 8 a = y 7 Rcon (7) = 40 00 00 00 y 7 ⊕ Rcon(7) = 46 d 3 df 8 a = z 7 w 28 = w 24 ⊕ z 7 = 37 14 93 48 w 29 = w 28 ⊕ w 25 = bb 3 d e 7 f 7 w 30 = w 29 ⊕ w 26 = 38 d 8 08 a 5 w 31 = w 30 ⊕ w 27 = f 7 7 d a 1 4 a Rot. Word (w 31) = 7 d a 1 4 a f 7 = x 8 Sub. Word (x 8) = ff 32 d 6 68 = y 8 Rcon (8) = 80 00 00 00 y 8 ⊕ Rcon(8) = 7 f 32 d 6 68 = z 8 w 32 = w 28 ⊕ z 8 = 48 26 45 20 w 33 = w 32 ⊕ w 29 = f 3 1 b a 2 d 7 w 34 = w 33 ⊕ w 30 = cb c 3 aa 72 w 35 = w 34 ⊕ w 32 = 3 c be 0 b 3 Rot. Word (w 35) = be 0 b 38 3 c = x 9 Sub. Word (x 9) = ae 2 b 07 eb = y 9 Rcon (9) = 1 B 00 00 00 y 9 ⊕ Rcon (9) = b 5 2 b 07 eb = z 9 w 36 = w 32 ⊕ z 9 = fd 0 d 42 cb w 37 = w 36 ⊕ w 33 = 0 e 16 e 0 1 c w 38 = w 37 ⊕ w 34 = c 5 d 5 4 a 6 e w 39 = w 38 ⊕ w 35 = f 9 6 b 41 56 Rot. Word (w 39) = 6 b 41 56 f 9 = x 10 Sub. Word (x 10) = 7 f 83 b 1 99 = y 10 Rcon (10) = 36 00 00 00 y 10 ⊕ Rcon (10) = 49 83 b 1 99 = z 10 w 40 = w 36 ⊕ z 10 = b 4 8 e f 3 52 w 41 = w 40 ⊕ w 37 = ba 98 13 4 e w 42 = w 41 ⊕ w 38 = 7 f 4 d 59 20 w 43 = w 42 ⊕ w 39 = 86 26 18 76 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

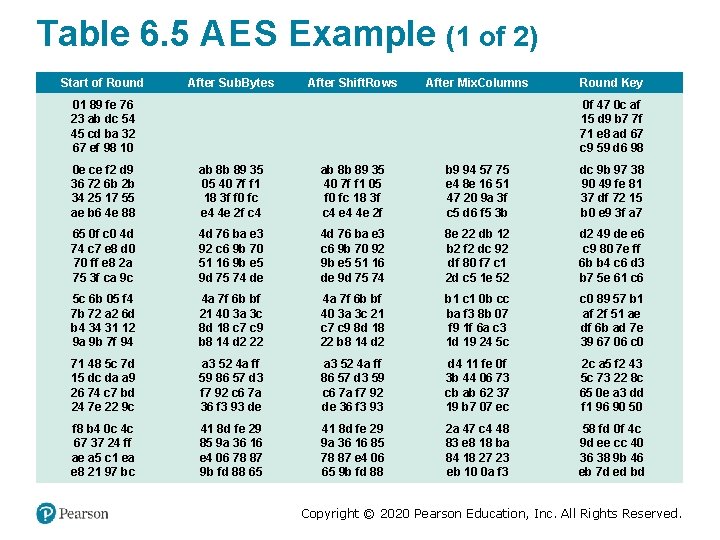
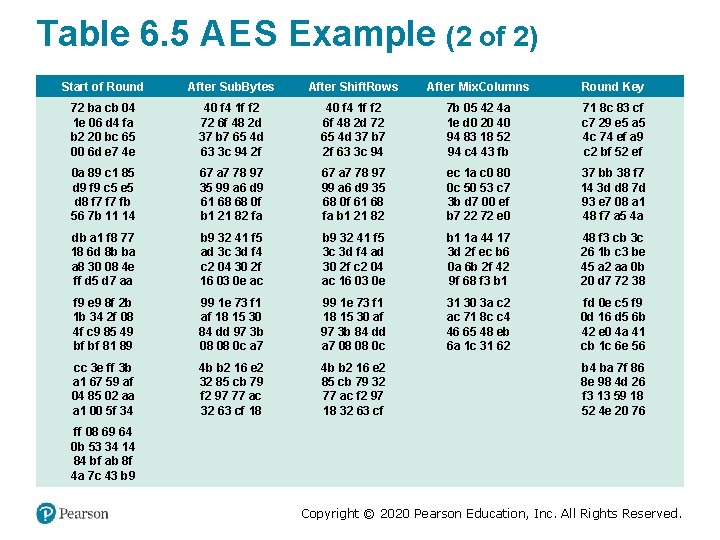
Table 6. 5 A E S Example (1 of 2) Start of Round After Sub. Bytes After Shift. Rows After Mix. Columns 01 89 fe 76 23 ab dc 54 45 cd ba 32 67 ef 98 10 Round Key 0 f 47 0 c af 15 d 9 b 7 7 f 71 e 8 ad 67 c 9 59 d 6 98 0 e ce f 2 d 9 36 72 6 b 2 b 34 25 17 55 ae b 6 4 e 88 ab 8 b 89 35 05 40 7 f f 1 18 3 f f 0 fc e 4 4 e 2 f c 4 ab 8 b 89 35 40 7 f f 1 05 f 0 fc 18 3 f c 4 e 4 4 e 2 f b 9 94 57 75 e 4 8 e 16 51 47 20 9 a 3 f c 5 d 6 f 5 3 b dc 9 b 97 38 90 49 fe 81 37 df 72 15 b 0 e 9 3 f a 7 65 0 f c 0 4 d 74 c 7 e 8 d 0 70 ff e 8 2 a 75 3 f ca 9 c 4 d 76 ba e 3 92 c 6 9 b 70 51 16 9 b e 5 9 d 75 74 de 4 d 76 ba e 3 c 6 9 b 70 92 9 b e 5 51 16 de 9 d 75 74 8 e 22 db 12 b 2 f 2 dc 92 df 80 f 7 c 1 2 d c 5 1 e 52 d 2 49 de e 6 c 9 80 7 e ff 6 b b 4 c 6 d 3 b 7 5 e 61 c 6 5 c 6 b 05 f 4 7 b 72 a 2 6 d b 4 34 31 12 9 a 9 b 7 f 94 4 a 7 f 6 b bf 21 40 3 a 3 c 8 d 18 c 7 c 9 b 8 14 d 2 22 4 a 7 f 6 b bf 40 3 a 3 c 21 c 7 c 9 8 d 18 22 b 8 14 d 2 b 1 c 1 0 b cc ba f 3 8 b 07 f 9 1 f 6 a c 3 1 d 19 24 5 c c 0 89 57 b 1 af 2 f 51 ae df 6 b ad 7 e 39 67 06 c 0 71 48 5 c 7 d 15 dc da a 9 26 74 c 7 bd 24 7 e 22 9 c a 3 52 4 a ff 59 86 57 d 3 f 7 92 c 6 7 a 36 f 3 93 de a 3 52 4 a ff 86 57 d 3 59 c 6 7 a f 7 92 de 36 f 3 93 d 4 11 fe 0 f 3 b 44 06 73 cb ab 62 37 19 b 7 07 ec 2 c a 5 f 2 43 5 c 73 22 8 c 65 0 e a 3 dd f 1 96 90 50 f 8 b 4 0 c 4 c 67 37 24 ff ae a 5 c 1 ea e 8 21 97 bc 41 8 d fe 29 85 9 a 36 16 e 4 06 78 87 9 b fd 88 65 41 8 d fe 29 9 a 36 16 85 78 87 e 4 06 65 9 b fd 88 2 a 47 c 4 48 83 e 8 18 ba 84 18 27 23 eb 10 0 a f 3 58 fd 0 f 4 c 9 d ee cc 40 36 38 9 b 46 eb 7 d ed bd Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Table 6. 5 A E S Example (2 of 2) Start of Round After Sub. Bytes After Shift. Rows After Mix. Columns Round Key 72 ba cb 04 1 e 06 d 4 fa b 2 20 bc 65 00 6 d e 7 4 e 40 f 4 1 f f 2 72 6 f 48 2 d 37 b 7 65 4 d 63 3 c 94 2 f 40 f 4 1 f f 2 6 f 48 2 d 72 65 4 d 37 b 7 2 f 63 3 c 94 7 b 05 42 4 a 1 e d 0 20 40 94 83 18 52 94 c 4 43 fb 71 8 c 83 cf c 7 29 e 5 a 5 4 c 74 ef a 9 c 2 bf 52 ef 0 a 89 c 1 85 d 9 f 9 c 5 e 5 d 8 f 7 fb 56 7 b 11 14 67 a 7 78 97 35 99 a 6 d 9 61 68 68 0 f b 1 21 82 fa 67 a 7 78 97 99 a 6 d 9 35 68 0 f 61 68 fa b 1 21 82 ec 1 a c 0 80 0 c 50 53 c 7 3 b d 7 00 ef b 7 22 72 e 0 37 bb 38 f 7 14 3 d d 8 7 d 93 e 7 08 a 1 48 f 7 a 5 4 a db a 1 f 8 77 18 6 d 8 b ba a 8 30 08 4 e ff d 5 d 7 aa b 9 32 41 f 5 ad 3 c 3 d f 4 c 2 04 30 2 f 16 03 0 e ac b 9 32 41 f 5 3 c 3 d f 4 ad 30 2 f c 2 04 ac 16 03 0 e b 1 1 a 44 17 3 d 2 f ec b 6 0 a 6 b 2 f 42 9 f 68 f 3 b 1 48 f 3 cb 3 c 26 1 b c 3 be 45 a 2 aa 0 b 20 d 7 72 38 f 9 e 9 8 f 2 b 1 b 34 2 f 08 4 f c 9 85 49 bf bf 81 89 99 1 e 73 f 1 af 18 15 30 84 dd 97 3 b 08 08 0 c a 7 99 1 e 73 f 1 18 15 30 af 97 3 b 84 dd a 7 08 08 0 c 31 30 3 a c 2 ac 71 8 c c 4 46 65 48 eb 6 a 1 c 31 62 fd 0 e c 5 f 9 0 d 16 d 5 6 b 42 e 0 4 a 41 cb 1 c 6 e 56 cc 3 e ff 3 b a 1 67 59 af 04 85 02 aa a 1 00 5 f 34 4 b b 2 16 e 2 32 85 cb 79 f 2 97 77 ac 32 63 cf 18 4 b b 2 16 e 2 85 cb 79 32 77 ac f 2 97 18 32 63 cf b 4 ba 7 f 86 8 e 98 4 d 26 f 3 13 59 18 52 4 e 20 76 ff 08 69 64 0 b 53 34 14 84 bf ab 8 f 4 a 7 c 43 b 9 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

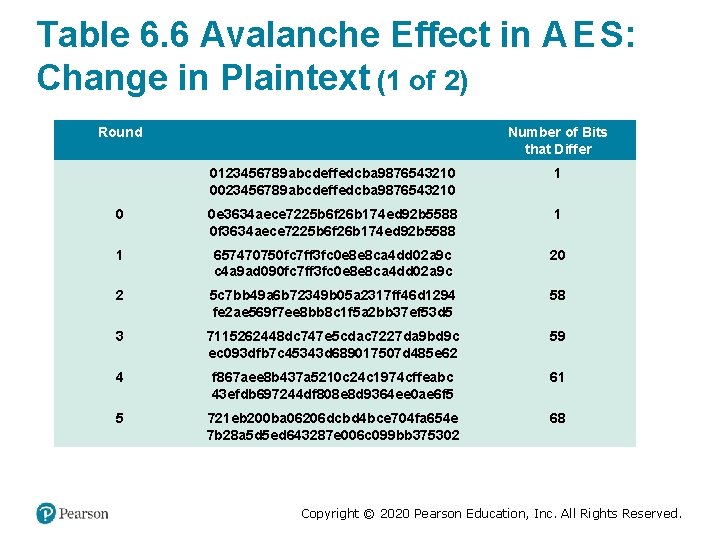
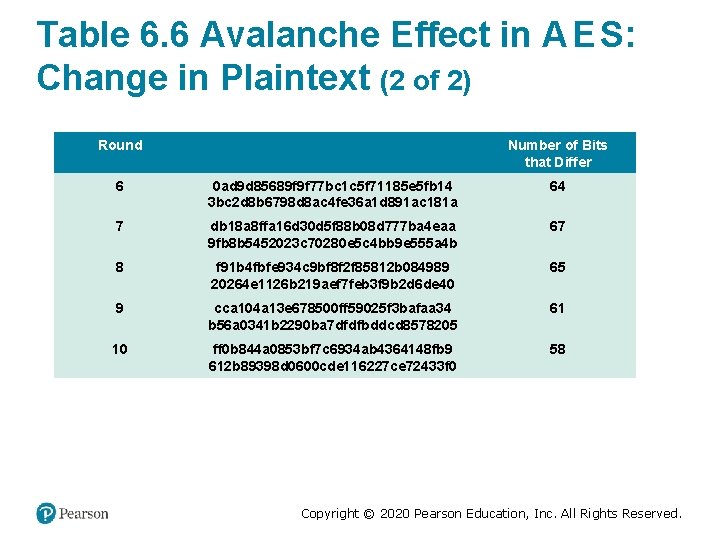
Table 6. 6 Avalanche Effect in A E S: Change in Plaintext (1 of 2) Round Number of Bits that Differ 0123456789 abcdeffedcba 9876543210 0023456789 abcdeffedcba 9876543210 1 0 0 e 3634 aece 7225 b 6 f 26 b 174 ed 92 b 5588 0 f 3634 aece 7225 b 6 f 26 b 174 ed 92 b 5588 1 1 657470750 fc 7 ff 3 fc 0 e 8 e 8 ca 4 dd 02 a 9 c c 4 a 9 ad 090 fc 7 ff 3 fc 0 e 8 e 8 ca 4 dd 02 a 9 c 20 2 5 c 7 bb 49 a 6 b 72349 b 05 a 2317 ff 46 d 1294 fe 2 ae 569 f 7 ee 8 bb 8 c 1 f 5 a 2 bb 37 ef 53 d 5 58 3 7115262448 dc 747 e 5 cdac 7227 da 9 bd 9 c ec 093 dfb 7 c 45343 d 689017507 d 485 e 62 59 4 f 867 aee 8 b 437 a 5210 c 24 c 1974 cffeabc 43 efdb 697244 df 808 e 8 d 9364 ee 0 ae 6 f 5 61 5 721 eb 200 ba 06206 dcbd 4 bce 704 fa 654 e 7 b 28 a 5 d 5 ed 643287 e 006 c 099 bb 375302 68 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Table 6. 6 Avalanche Effect in A E S: Change in Plaintext (2 of 2) Round Number of Bits that Differ 6 0 ad 9 d 85689 f 9 f 77 bc 1 c 5 f 71185 e 5 fb 14 3 bc 2 d 8 b 6798 d 8 ac 4 fe 36 a 1 d 891 ac 181 a 64 7 db 18 a 8 ffa 16 d 30 d 5 f 88 b 08 d 777 ba 4 eaa 9 fb 8 b 5452023 c 70280 e 5 c 4 bb 9 e 555 a 4 b 67 8 f 91 b 4 fbfe 934 c 9 bf 8 f 2 f 85812 b 084989 20264 e 1126 b 219 aef 7 feb 3 f 9 b 2 d 6 de 40 65 9 cca 104 a 13 e 678500 ff 59025 f 3 bafaa 34 b 56 a 0341 b 2290 ba 7 dfdfbddcd 8578205 61 10 ff 0 b 844 a 0853 bf 7 c 6934 ab 4364148 fb 9 612 b 89398 d 0600 cde 116227 ce 72433 f 0 58 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

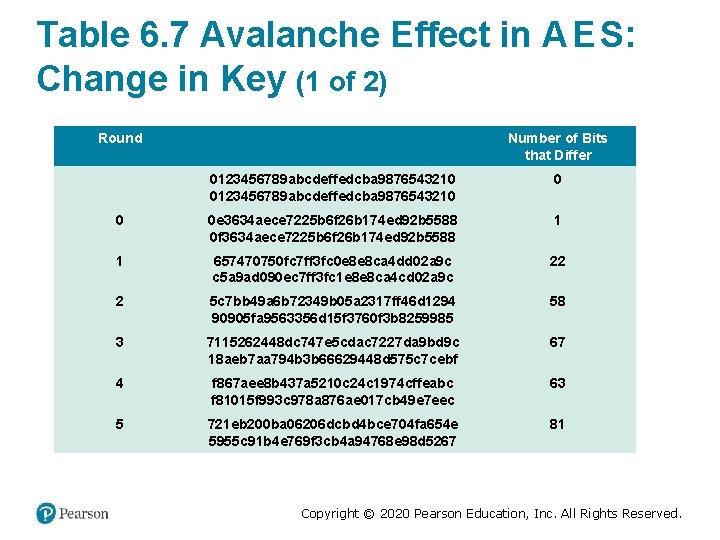
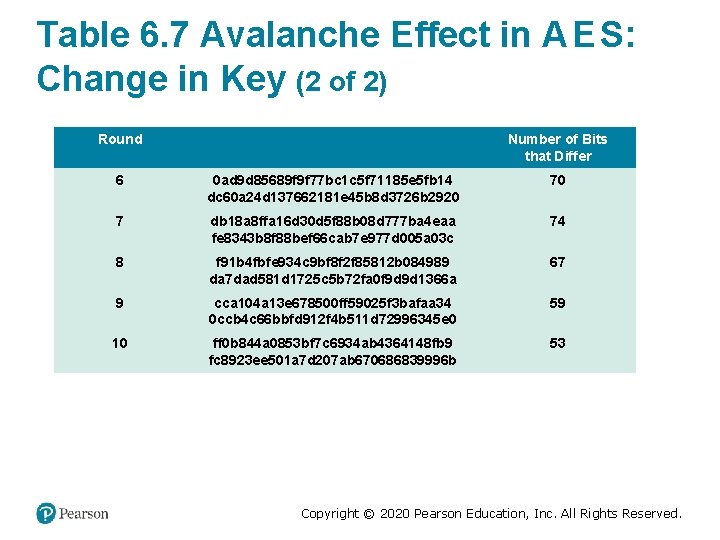
Table 6. 7 Avalanche Effect in A E S: Change in Key (1 of 2) Round Number of Bits that Differ 0123456789 abcdeffedcba 9876543210 0 0 0 e 3634 aece 7225 b 6 f 26 b 174 ed 92 b 5588 0 f 3634 aece 7225 b 6 f 26 b 174 ed 92 b 5588 1 1 657470750 fc 7 ff 3 fc 0 e 8 e 8 ca 4 dd 02 a 9 c c 5 a 9 ad 090 ec 7 ff 3 fc 1 e 8 e 8 ca 4 cd 02 a 9 c 22 2 5 c 7 bb 49 a 6 b 72349 b 05 a 2317 ff 46 d 1294 90905 fa 9563356 d 15 f 3760 f 3 b 8259985 58 3 7115262448 dc 747 e 5 cdac 7227 da 9 bd 9 c 18 aeb 7 aa 794 b 3 b 66629448 d 575 c 7 cebf 67 4 f 867 aee 8 b 437 a 5210 c 24 c 1974 cffeabc f 81015 f 993 c 978 a 876 ae 017 cb 49 e 7 eec 63 5 721 eb 200 ba 06206 dcbd 4 bce 704 fa 654 e 5955 c 91 b 4 e 769 f 3 cb 4 a 94768 e 98 d 5267 81 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Table 6. 7 Avalanche Effect in A E S: Change in Key (2 of 2) Round Number of Bits that Differ 6 0 ad 9 d 85689 f 9 f 77 bc 1 c 5 f 71185 e 5 fb 14 dc 60 a 24 d 137662181 e 45 b 8 d 3726 b 2920 70 7 db 18 a 8 ffa 16 d 30 d 5 f 88 b 08 d 777 ba 4 eaa fe 8343 b 8 f 88 bef 66 cab 7 e 977 d 005 a 03 c 74 8 f 91 b 4 fbfe 934 c 9 bf 8 f 2 f 85812 b 084989 da 7 dad 581 d 1725 c 5 b 72 fa 0 f 9 d 9 d 1366 a 67 9 cca 104 a 13 e 678500 ff 59025 f 3 bafaa 34 0 ccb 4 c 66 bbfd 912 f 4 b 511 d 72996345 e 0 59 10 ff 0 b 844 a 0853 bf 7 c 6934 ab 4364148 fb 9 fc 8923 ee 501 a 7 d 207 ab 670686839996 b 53 Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

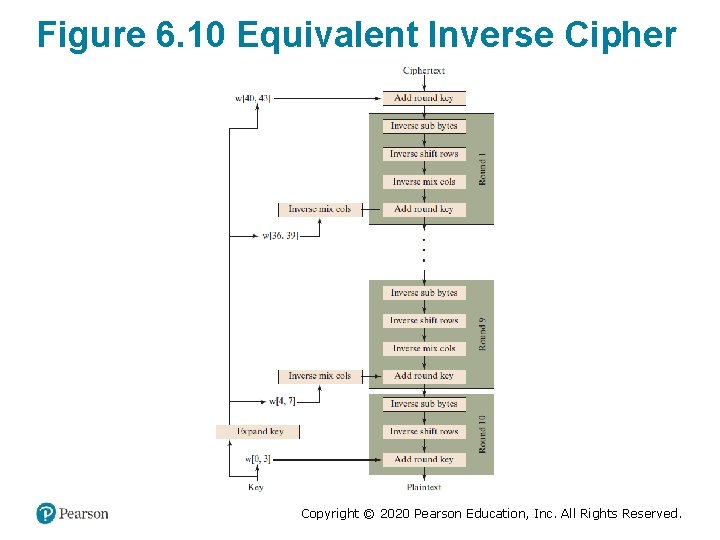
A E S Implementation • A E S decryption cipher is not identical to the encryption cipher – The sequence of transformations differs although the form of the key schedules is the same – Has the disadvantage that two separate software or firmware modules are needed for applications that require both encryption and decryption • Two separate changes are needed to bring the decryption structure in line with the encryption structure • The first two stages of the decryption round need to be interchanged • The second two stages of the decryption round need to be interchanged Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Interchanging Inv. Shift. Rows and Inv Sub. Bytes • Inv. Shift. Rows affects the sequence of bytes in State but does not alter byte contents and does not depend on byte contents to perform its transformation • Inv. Sub. Bytes affects the contents of bytes in State but does not alter byte sequence and does not depend on byte sequence to perform its transformation Thus, these two operations commute and can be interchanged Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Interchanging Add. Round. Key and Inv. Mix. Columns • The transformations Add. Round. Key and Inv. Mix. Columns do not alter the sequence of bytes in State • If we view the key as a sequence of words, then both Add. Round. Key and Inv. Mix. Columns operate on State one column at a time • These two operations are linear with respect to the column input Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Figure 6. 10 Equivalent Inverse Cipher Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Implementation Aspects (1 of 2) • AES can be implemented very efficiently on an 8 -bit processor • Add. Round. Key is a bytewise XOR operation • Shift. Rows is a simple byte-shifting operation • Sub. Bytes operates at the byte level and only requires a table of 256 bytes • Mix. Columns requires matrix multiplication in the field GF(28), which means that all operations are carried out on bytes Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Implementation Aspects (2 of 2) • Can efficiently implement on a 32 -bit processor – Redefine steps to use 32 -bit words – Can precompute 4 tables of 256 -words – Then each column in each round can be computed using 4 table lookups + 4 XORs – At a cost of 4 Kb to store tables • Designers believe this very efficient implementation was a key factor in its selection as the AES cipher Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Summary • Present an overview of the general structure of Advanced Encryption Standard (AES) • Understand the four transformations used in AES • Explain the AES key expansion algorithm • Understand the use of polynomials with coefficients in GF(28) Copyright © 2020 Pearson Education, Inc. All Rights Reserved.

Copyright This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching their courses and assessing student learning. Dissemination or sale of any part of this work (including on the World Wide Web) will destroy the integrity of the work and is not permitted. The work and materials from it should never be made available to students except by instructors using the accompanying text in their classes. All recipients of this work are expected to abide by these restrictions and to honor the intended pedagogical purposes and the needs of other instructors who rely on these materials. Copyright © 2020 Pearson Education, Inc. All Rights Reserved.