Cryptography and Network Security M Sakalli Source Third

Cryptography and Network Security M. Sakalli Source: Third Edition by William Stallings And Modified Lecture Slides of Lawrie Brown

Sun-Tsu’s Chinese Remainder Thr Ø States that when the moduli of a system of linear congruencies are pairwise prime, there is a unique solution of the system modulo, the product of the moduli. Ø ax = b (mod m). The 1 st Century CE (Common Era, ~400 AD), the Chinese mathematician Sun Tsu Suan-Ching asking the following problem: “There are certain things whose number is unknown. When divided by 3, the remainder is 2; when divided by 5, the remainder is 3; and when divided by 7, the remainder is 2. What will be the number of things? ” Discrete Math Kenneth H Rosen, page 186. Ø x = 2 mod(3) Ø x = 3 mod(5) Ø x = 2 mod(7) Let m 1, m 2, …, mn be (pairwise) relatively prime numbers. Then the system: Ø x = a 1 mod (m 1) = a 2 mod (m 2) = …. = an mod (mn) Ø Has a unique solution modulo Ø M = m 1 m 2 … mn. The CRT says that only one number of x mod(3 x 5 x 7) satisfies all eqns. x = 23 (mod 105), . x = 23 = 7*3 + 2 = 2 (mod 3), x = 23 = 4*5 + 3 = 3 (mod 5), x = 23 = 3*7 + 2 = 2 (mod 7)

How to construct the solution in mod(M) 23 mod(105) = 23 + 105 n { …, -292, -187, -82, 23, 128, 233, 338, …} Therefore, all these congruent numbers are solutions of Sun-Tsu’s three equations. • • i. ii. i. M = (πk=1: n mi) = m 1 m 2 … mn all mk’s have to be pairwise relatively prime. For each equation of x= ak mod(mk) calculate Mk =M/mk; all mi except for mk. yk inverse of Mk from Mk yk=1 mod(mk)=(Mkmod(mk)) yk x = 2 mod (3) (5*7) y 1 = 1 mod(3) y 1 =2. x = 3 mod (5) (3*7) y 2 = 1 mod(5) y 2 =1 x = 2 mod (7) (3*5) y 3 = 1 mod(7) y 3 =1 x = Σ(ai. Miyi) = (a 1 M 1 y 1 + a 2 M 2 y 2 + a 3 M 3 y 3) = 233 = 23 mod(105)

Why does this work? (without going into detail) Suppose the solution x and “mod” it by m 1: M 1 y 1 is equal to a 1, since M 1 y 1 = 1 mod (m 1). M 2 y 2, M 3 y 3 , …, every other term is zero mod(m 1), since MK is a multiple of m 1. x = a 1 M 1 y 1 + a 2 M 2 y 2 + … + an. Mnyn. = 2 (5*7) 2 + 3 (3*7) 1 + 2 (3*5) 1 But would be true for any of the mk. Therefore, x satisfies all of the equations. One of the most useful results of number theory is in speeding up some operations in the RSA public-key scheme, since it allows to perform calculations modulo factors, and then combine the answers to get the actual result. Since the computational cost is proportional to size, such manipulating is faster than working in the full size modulus, ie when M is 150 digits or more. However it is necessary to know beforehand the factorization of M. operations in n-tuples. See worked examples in Stallings section 8. 4.

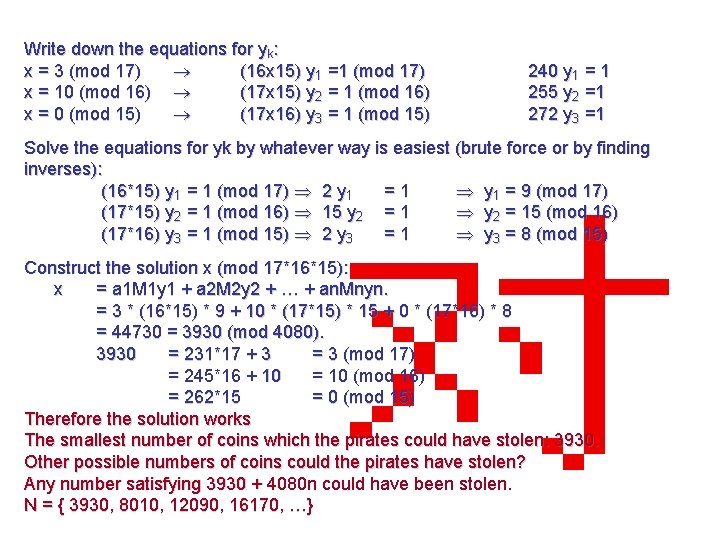
Ancient Chinese Pirates: A band of 17 pirates stole a sack of gold coins. When they tried to divide the fortune into equal portions, 3 coins remained. In the ensuing brawl over who should get the extra coins, one pirate was killed. The wealth was redistributed, but this time an equal division left 10 coins. Again an argument developed in which another pirate was killed, but now the fortune could be evenly distributed. What was the least number of coins which could have been stolen? What are all possible numbers of coins which could have been stolen? If x is the number of coins, it has to satisfy the following modular equations: x = 3 mod (17) x = 10 mod (16) x = 0 mod (15) These numbers are relatively prime, so the Chinese Remainder Theorem says there IS a solution mod 17*16*15 = 4080. It might have been possible there that there is NO SOLUTION.

Write down the equations for yk: x = 3 (mod 17) (16 x 15) y 1 =1 (mod 17) x = 10 (mod 16) (17 x 15) y 2 = 1 (mod 16) x = 0 (mod 15) (17 x 16) y 3 = 1 (mod 15) 240 y 1 = 1 255 y 2 =1 272 y 3 =1 Solve the equations for yk by whatever way is easiest (brute force or by finding inverses): (16*15) y 1 = 1 (mod 17) 2 y 1 =1 y 1 = 9 (mod 17) (17*15) y 2 = 1 (mod 16) 15 y 2 = 15 (mod 16) (17*16) y 3 = 1 (mod 15) 2 y 3 =1 y 3 = 8 (mod 15) Construct the solution x (mod 17*16*15): x = a 1 M 1 y 1 + a 2 M 2 y 2 + … + an. Mnyn. = 3 * (16*15) * 9 + 10 * (17*15) * 15 + 0 * (17*16) * 8 = 44730 = 3930 (mod 4080). 3930 = 231*17 + 3 = 3 (mod 17) = 245*16 + 10 = 10 (mod 16) = 262*15 = 0 (mod 15) Therefore the solution works The smallest number of coins which the pirates could have stolen: 3930. Other possible numbers of coins could the pirates have stolen? Any number satisfying 3930 + 4080 n could have been stolen. N = { 3930, 8010, 12090, 16170, …}

• Pairs representing nonnegative integers less than 12, when represented with ordered pairs, first remainder of mod(3), and the second remainder of mod(4), 0={0, 0}, 1={1, 1}, 2={ }. . 3={0, 3} 4={1, 0}, …………. … 11={2, 3} • By CRT, n-tuples on a processor will run quicker, ie, every nonnegative integer less than 100; using moduli of pairwise relatively prime integers: 99, 98, 97, 95. . Any integer < 89403930 can be represented uniquely. Suppose two numbers 123684 (33, 8, 9, 89) and 413456 (32, 92, 42, 16). . Find remainder (congruencies) for each module and (proceed with an operation) sum in each tuple and merge the results to reach the final sum as 537140. . Unique nonnegative solution. • Particular good (applicable) choices of moduli with large integers are of the form 2 k -1, (binary), k a positive integer. Binary operations, the second reason is that gcd(2 a -1, 2 b -1) =2 gcd(a, b) -1, (proof of which is in page 112 104 Number Theory Problems, source in our webpage)

Systems of Linear Modular Equations: a 1 x = b 1 (mod m 1) a 2 x = b 2 (mod m 2) …. anx = bn (mod mn) Solve each equation aix = bi (mod mi) individually. a 1 x = b 1 (mod m 1) x = c 1 (mod m 1) a 2 x = b 1 (mod m 2) x = c 2 (mod m 2) …. …. anx = b 1 n (mod mn) x = cn (mod mn) Solve the following set of simultaneous congruences: i) x = 5 (mod 6) iii) 2 x = 1 (mod 5) x = 4 (mod 11) 3 x = 9 (mod 6) x = 3 (mod 17) 4 x = 1 (mod 7) 5 x = 9 (mod 11) ii) x = 5 (mod 11) x = 14 (mod 29) x = 15 (mod 21) Question iii is a bit harder. How badly do you want an A+?

Homeworks: Answer Brahmagupta’s question: (7 th century AD) An old woman goes to market and a horse steps on her basket and crashes the eggs. The rider offers to pay for the damages and asks her how many eggs she had brought. She does not remember the exact number, but when she had taken them out two at a time, there was one egg left. The same happened when she picked them out three, four, five, and six at a time, but when she took them seven at a time they came out even. What is the smallest number of eggs she could have had? What other possible number of eggs could she have? [Hint: x = 1 (mod 2, 3, 4, 5, 6), x = 0 (mod 7). ]

Pseudoprimes • Suppose integers larger than 235, in our computers. . Moduli of 235 -1, 234 -1, 233 -1, 231 -1, 229 -1, 223 -1 are pairwise prime, giving in the possibility working with the integers (not exceeding) 2184. • An integer n is prime when not divisible by any prime smaller than sqrt(n). ie 101, easy. . But inefficient. • Chinese mathematicians: believed that p is prime whenever congruence of 2 p-1 = mod(p) holds but couldn’t show for composite numbers. • Fermat shows that the congruence holds when n is prime. Fermat’s Little theorem, if p is prime and a is an integer not divisible with p, then ap-1 = 1 mod(p), besides for every integer a, ap = a mod(p). • The corollary, if 2 n-1 = 1 mod(n), n is always prime, is not always correct. • Composite positive integers for which 2 n-1 = 1 mod(n) holds are pseudoprime numbers, for example for n=341=11*31, n is pseudoprime to base 2.

• Definition: for n, a>0 integers, and if n is composite such that an-1 = 1 mod(n), then n is a pseudoprime to a. • So if n satisfies, 2 n-1 = 1 mod(n), n is either prime or pseudoprime to the base 2, performing similar tests for the other bases coprime to n. • More than 40*106 prime numbers <1010 -1, but only 14884 pseudoprime numbers to the base 2. • Not easy to distinguish, due to the other composite numbers that pass all the tests with bases; gcd(b, n)=1. • Composite integer numbers n satisfying both bn-1 = 1 mod(n) and gcd(b, n), are Carmichael numbers. (6 k + 1)(12 k + 1)(18 k + 1), where k is prime, not proved for large numbers. Example 561=3*11*17, if gcd(b, 561) = 1; then gcd(b, 3) = gcd(b, 11) = gcd(b, 17) = 1; 561 passes fermat’s little thr, b 3 -1 = 1 mod(3), b 11 -1 = 1 mod(11), = b 17 -1 = 1 mod(17) • b 560 = b(2)280 = 1 mod(3), b 560 = b(10)56 = 1 mod(11), b 560 = b(16)35 = 1 mod(17) • b 560 = 1 mod(561), for every b with gcd(b, 561) = 1. there are many infinite number of carmichael numbers.

Magicicada Species: Wikipedia. New Lease of Life for Prime Numbers Two discoveries in the last 30 years. One is amusing, the other important in the business world. Periodic cicadas - a type of insect found in North America - hibernate for many years, lying dormant in the ground. After a long period, they emerge to begin a new life. It has been found that there are two distinct types of Cicada, those that remain dormant for 13 years and those that choose to sleep for 17 years. It is no coincidence that these two numbers are primes! This is explained in the Guide entry on cicadas.

Euler Totient Function Φ(n) • coprimes to n form a group • reduced set of residues is those numbers (residues) which are relatively prime to n – eg for n=10, complete set of residues is – {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} reduced set of residues is {1, 3, 7, 9} • to compute Φ(n): exclude every fold of its primes. . and count excluded ones. . Theorem 1. If p is prime then Φ(p) = p – 1. – – for p (p prime) ø(p) = p-1 for p. q (p, q prime) ø(p. q) = ø(q)=(p-1)(q-1) Theorem 2. If gcd(n, m) = 1, then Φ(nm) = Φ(n) · Φ(m). • Examples: Φ(3) and Φ(5) above. • Relatively prime, so theorem claims that Φ(15) = Φ(3) · Φ(5) = 2 · 4 = 8, which is correct.

Euler Totient Function Φ(n) • Proof: Consider the # of integers that are not relatively prime in {0…(pq-1)} {p, 2 p, . . . , (q-1)p}, and {q, 2 q, . . . , (p-1)q}, therefore Φ(p. q) = p. q-(p-1)-(q-1)-1 = p. q-p-q+1 = (p-1)(q-1) • eg. – Φ(37) = 36 – Φ(21) = (3– 1)×(7– 1) = 2× 6 = 12 Theorem 3. If p is prime and n ≥ 1, then Φ(pn) = pn – pn-1. • Examples: Consider p = 3 and n = 2. Integers relatively prime to 9: {1, 2, 4, 5, 7, 8}<9. • Φ(52) = 20, inspect: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Theorem 4 (Euler's Theorem). For any integer n > 1, if gcd(a, n) = 1, then aΦ(n) ≡ aΦ(n)mod N ≡ 1 (mod n). . • Examples: For n = 10, Φ(10) = 4. gcd(a, n) = 1: • a = 1: 14 = 1 • a = 3: 34 = 81 • a = 7: 74 = 2401 all of these are ≡ 1 (mod 10) • a = 9: 94 = 6561 • a = 17: 174 = 83521 • a = 57: 574 = 10556001 • n=11, a=2, ø(11)=10 210=1024=1 mod(11) Theorem 5 (Fermat's Theorem). If p is prime and gcd(a, p) = 1, then ap-1 ≡ 1 (mod p). • From Euler's Theorem by applying Theorems 1 and 4. • Example: p = 5 and a = 6, which is relatively prime to 5. 65 -1 ≡ 1 (mod 5) = 1296.

Theorem 6. For any n > 1, if gcd(a, n) = 1, then the equation ax ≡ 1 (mod n) has a unique solution, modulo n. From the gcd identity, there is a linear combination of a and n such that 1 = ax + ny. Since n divides ny evenly, ax mod n must be 1. • Example: • 3· 0 ≡ 0 mod 5 • 3· 1 ≡ 3 mod 5 • 3· 2 ≡ 1 mod 5 (for a = 3, n = 5, the solution is x = 2) • 3· 3 ≡ 4 mod 5 • 3· 4 ≡ 2 mod 5 Theorem 7. From CRT, if gcd(p, q) = 1, then for all integers x and a, x ≡ a (mod p) and x ≡ a (mod q) if and only if x ≡ a mod(pq). This is a corollary of the Chinese Remainder Theorem. • Example: gcd(3, 5) = 1 • 32 ≡ 2 mod 15 • 32 ≡ 2 mod 3 • 32 ≡ 2 mod 5

• Factoring a number n: n=a b c • Relatively hard when compared to multiplying the factors together to generate the number • Prime factorisation of a number n – eg. 91=7 13; 3600=24 32 52 • two numbers are relatively prime to each other if. . • Conversely; gcd the common least powers of prime factorizations. – 300=21 31 52 18=21 32 hence GCD(18, 300)=21 31 50=6 • Fermat’s Little Theorem: ap-1 = 1 mod p = 1 where p is prime and naturally gcd(a, p)=1

The RSA Algorithm • • Rivest, Shamir, Adleman, MIT, 1978 Reference: From Cormen et al at end of handout] 1. Select two large primes p and q such that p ≠ q. Typical values might be integers with 200 digits. RSA currently recommends a module of at least 768 bits long. 2. Compute N = pq. 3. Select an exponent odd integer Ke relatively prime to Φ(N) = (p – 1)(q – 1), where Φ(N) is kept private. (Theorem 2 and 1). Finding p and q, probabilistic primality test. However this can not be done for 400 digits in a reasonable time. 4. Find Kd such that Ke*Kd ≡ 1 (mod Φ(N)). Theorem 6: a solution for Kd exists and that given Ke and Φ(N), it is uniquely defined. (Euclid's Algorithm), Kd and Ke are multiplicative inverses in modulo Φ(N), since their product modulo Φ(N) is 1. Note that Kd is easy to compute only if one knows the value of Φ(N) which is essentially the same as knowing the values of P and Q. 5. Publish Ke and N as the public key. 6. Keep secret Kd, which along with N, is the private key.

The RSA Algorithm Finally: Ke (made public) and Kd(kept private), • If PT is a numeric encoding of a block of plaintext, the cipher text is CT = PTKe mod N. • PT = CTKd mod N. = (PT(Ke))Kd mod N. • P = 5, Q=11. N = P*Q = 55 • Message length encoded < log(N)= 5 the length of message. A larger message, break it is into blocks. • Φ(N) = (P-1)*(Q-1) = 40. • Ke, relatively prime, gcd(Ke, Φ(N)): Ke=13 • Kd, such that Kd * Ke =1 mod(Φ(N)): Kd=37

The RSA Algorithm • Multiplying P by Q is easy: the number of operations depends on the number of bits in P and Q. • For example, multiplying two 384 -bit numbers takes approximately 3842 = 147, 456 bit operations • If one knows only N, factoring P and Q is hard: in essence, the # of operations depends on the value of N. The simplest method for factoring a 768 -bit number takes about 2384 3. 94 *10115 trial divisions, 285 3. 87 1025 trial divisions, 241 219, 000, 000 trial divisions • A quick factoring algorithm of large number M hasn’t been done yet. And also the absence or impossibility of such an algorithm not proven yet. • Peter Shor has devised a very fast factoring algorithm for a quantum computer, if anyone manages to build one. • ***Prove that MKe. Kd mod(N) = M mod(N). In other words Pub(Priv(M)) = Priv(Pub(M)) = M. • It turns out that there are feasible attacks on RSA. To guarantee security, a very large modulus must be used and some preprocessing of the message should be done.

Euler’s theorem • For every a and n relatively prime, aΦ(n) =1 mod(n). • For example, n=10, a=3, or n=11, a=21 • For n prime, Φ(n) = n-1; from Fermat’s thr a(n-1) = 1 mod(n) a(n) = n mod(n). • It holds for any integer n, relatively prime numbers R={x 1, …, xΦ(n)} to n, a R, S=a{x 1 mod(n), …, xΦ(n) mod(n)} = {ax 1, …, a xΦ(n)}, any of axi must be relatively prime to n, and less then n, since R and a are both prime to n. • There are no duplicates in S and πi=1: Φ(n) axi mod(n) aΦ(n) πi=1: Φ(n) xi aΦ(n) =1 mod(n) = = πi=1: Φ(n) xi, … πi=1: Φ(n) xi mod(n) aΦ(n)+1 =a mod(n).

Euler’s theorem • Corollary, n=pq, both primes, and 0<m<n, mΦ(n)+1 = m(p-1)(q-1)+1 =m mod(n) holds. If gcd(m, n) =1, by virtue of Euler’s thr it holds. Suppose gcd(m, n) not one, then n= pq, gcd(m, n)=1, means that, neither p nor q divides m. If m=c 1 p, (or m=c 2 q, where c is integer and c>0) then m and n cannot be relative therefore gcd(m, n) =not 1. • If gcd(m, q)=1, from Euler’s thr mΦ(q) = 1 mod(q), [mΦ(q)]Φ(p) = 1 mod(q) mΦ(n) = 1 +kq mΦ(n)+1 = m + kcpq = m + kcn mΦ(n)+1 = m mod(n) • Or an alternative way, mkΦ(n)+1 =[[mΦ(n) ]k m ]mod(n)= [1 k m] mod(q) =m mod(n)

Primality Testing • traditionally sieve using trial division – ie. divide by all numbers (primes) in turn less than the square root of the number – only works for small numbers • Miller Rabin Algorithm based on Fermat’s Theorem a(n-1) =1 mod(n) = 1 if n is prime. • Consider an odd number n>2, then n-1 is even number, therefore equal to 2 kq with k>0, q must be odd. Keep dividing n-1 by 2, k divisions, you’ve got the q, determine a number 1<a<n-1, compute 2 kq power of the number a, and check the equality to n-1 (line 5), or to 1 (line 3): • TEST (n) is: 1. Find integers k, q, k > 0, q odd, so that (n– 1)=2 kq; 2. Select a random integer a, 1<a<n– 1; 3. if aq mod n = 1 then return (“maybe prime"); 4. for j = 0 to k – 1 do j 5. if (a 2 q mod n = n-1) then return(" maybe prime ") 6. return ("composite")

Primality Testing If n is prime there is a smallest value of j, 0 j k, such that (a)^(2 jq)mod(n) = 1. For j=0, For 1 j k, aq-1 = 0, or n|(aq-1). a^(2 jq)mod(n) = 1 (a^(2(j-1)q)mod(n)-1)*(a^(2(j-1)q)mod(n)+1) = 1 n divides either side, by assumption j is the smallest such that n does not divide (a^(2(j-1)q)mod(n)-1), therefore n|(a^(2(j-1)q)mod(n)-1). Or equivalently a^(2(j-1)q)mod(n)=(-1)mod(n)=n-1; line 5.

Probabilistic Considerations • Millar-Rabin test returns inconclusive for (n-1)/4 < ¼ • if Miller-Rabin returns “composite” the number is definitely not prime otherwise is a prime or a pseudo-prime chance it detects a pseudo-prime is < ¼ • Therefore if test returns inclusive t times in succession. . then probability n is prime is 1 -4 -t… • Prime distribution: Considering distribution of the primes, “prime number theorem states that the primes near n are spaced on the average one every ln(n) integers”, so the is on the order of ln(n), even integers and fold of 5 are rejected. . So, 0. 4 ln(n), for example if the order of prime number is 2200, 0. 4 ln(n)=55 trials. Closely located ones, 1. 000. 061, 1. 000. 063 are primes.

Probabilistic Considerations of Millar-Rabin • n=29, 2 kq=28= 22 7, k=2; • a=10; – j=0, 107 mod(29)=17, neither 28, nor 1. . – j=1, (107)2 mod(29)=28, inconclusive, may be pr. . • a=2, – j=0, 27 mod(29)=12, – j=1, 214 mod(29)=28, inc. . • For all a’s this will give inconclusive, so n is a prime. . • • n=13*17=221, 2 kq=220= 22 55, k=2; a=5; – j=0, 555 mod(221)=112. . – j=1, (555)2 mod(221)=168, n returns composite. . • But if a would have been chosen as 21, – j=0, 217 mod(221)=200. . – j=1, 2114 mod(221)=220, returns inclusive, which points 221 as prime. . • In fact of the 220 integers, 1, 21, 47, 174, 200, 220 return inc. .

Primitive Roots

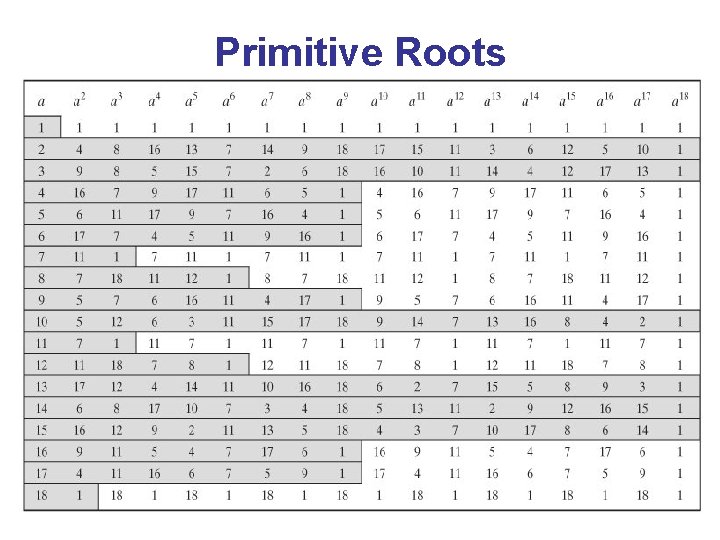
Primitive Roots • From Euler’s theorem have aø(n)mod n=1 • consider ammod n=1, and (a, n) relative prime GCD(a, n)=1 – at least one positive m<n satisfying ammod n=1, for example m = ø(n) or may be smaller, this is called the order of a (mod n). . – once powers reach m, cycle will repeat • if smallest is m= ø(n) then corresponding a is called a primitive root • To check if a number x is primitive root, it suffices to check xm=1 mod p, *** – the order of any x coprime to p has to be a divisor of (p − 1) since xp 1=1 mod p, *** following words are not clear yet to me too but the statement written is valid** --- if n is not a primitive root, then there exists a strict positive divisor m of p-1, such that p-1, xm=1 mod p, so there the statement we made suffices. . --- • if p is prime, then successive powers of a "generate" the group mod p

Primitive Roots • Example: from previous table, p=19, p-1 = 2. 32, divisors 1, 2, 3, 6, 9, 18, check a=10, 102=5, 103=12, 103=5, 106=11, 109=18, 1018=1 mod(19), so the smallest power of x, such that xm=1 mod p is 18, hence ordp(a) = ord 19(10)=18. • Check if the rule applies to a=5, 53=11, 59=1, . . Then will recycle the numbers periodically since 1018= 1 mod(19).

Primitive Roots • Similarly, you can do the rest of the homework by yourselves. The complete list of primitive roots is: – – – – mod 3 : 2 mod 5 : 2, 3 mod 7 : 3, 5 mod 11 : 2, 6, 7, 8 mod 13 : 2, 6, 7, 11 mod 17 : 3, 5, 6, 7, 10, 11, 12 mod 19 : 2, 3, 10, 13, 14, 15 • Once you have found '(p − 1) many primitive roots mod p, you are done, because mod p there are exactly '(p − 1) distinct primitive roots. • CHECK THIS.

Discrete Logarithms or Indices • Input: p - prime number, a- primitive root of p, b - a residue mod p. • Goal: Find k such that ak = b( mod p). (In other words, find the position of y in the large list of {a, a 2, . . . , aq-1}. • 14 is a primitive root of 19. • The powers of 14 (mod 19) are in order: 14 6 8 17 10 7 3 4 18 5 13 11 2 9 12 16 15 1 • For example L 14(5) = 10 mod 19, because 1410 = 5( mod 19). • the inverse problem to exponentiation is to find the discrete logarithm of a number modulo p • • • that is to find x where ax = b mod p written as x=loga b mod p or x=inda, p(b) if a is a primitive root then always exists, otherwise may not – x = log 3 4 mod 13 (x st 3 x = 4 mod 13) has no answer – x = log 2 3 mod 13 = 4 by trying successive powers • whilst exponentiation is relatively easy, finding discrete logarithms is generally a hard problem

Diffie-Hellman, 1976, Section 10. 2 of Stallings • • Based on the difficulty of computing discrete logarithms of large numbers. No known successful attack strategies. • • Two numbers public: a prime p, a primitive root q of P. User A chooses a random integer XA < q and computes YA = q. Xamod(p) for secret A (known only to itself) and similarly user B chooses XB < q and computes YB = q. Xbmod(p). . • Each exchanges YA and YB, while XA, XB remains private • Parties A and B compute K = YBXamod(p) and K= YAXbmod(p), respectively, • K= (YB)Xa mod p = (q. Xb)Xa mod p = (q. Xa)Xb mod p = (YA)Xb mod p • Attacking the secret key of user A for example will require opponent to calculate XA= indb, p(YA)= dlogb, p(YA)or the other way around. • Example p= 353 and a primitive root of 353, q = 3. Suppose A and B choose XA=97, XA= 233. • YA = 397 mod(353) = 40, YB = 3233 mod(353) = 248 • K= 160. . Attacker must 3 Xamod(353) = 40 or 3 Xbmod(353)=248. .

• RSA is more convenient because there is no need to distribute keys. • DES is within two orders of magnitude faster. • A viable combination is to distribute the secret keys using RSA, and then, for the bulk data to use DES. • Similar combination is implemented in the Pretty Good Privacy (PGP) method. • A number of public-key ciphers are based on the use of an abelian group. For example, Diffie-Hellman key exchange involves multiplying pairs of nonzero integers modulo a prime number p. Keys are generated by exponentiation over the group, with exponentiation defined as repeated multiplication.

Elliptic Curves Chapter 10. 3 and 10. 4. . • The same level of security but shorter key are possible. • An equation in two variables. For cryptography, the variables and coefficients are restricted to elements in a finite field, which results in the definition of a finite abelian group. • Elliptic curves are not ellipses. They are so named because described by cubic equations, similar to the circumference of an ellipse. In general, cubic equations for elliptic curves take the form of y 2 + axy + by = x 3 + cx 2 + dx + e. . • Limiting attention (Stallings) to y 2 = y 3 + ax + b is sufficient. y = sqrt(y 3 + ax + b)

El Gamal public-key cryptosystem • • • Secure against CT only attacks. Each party (say Bob) chooses the following parameters. p, large prime number, q- primitive root of p, made public. a random a {2, 3, . . . , p − 1}, private ¯= qa(mod p), made public. • Encrypting: Choose a random k {1, 3, . . . , p − 1} (a). Suppose message is a number x < p. • Epublic−k(x) = {qk(mod p), x · ¯k( mod p)}. • Two numbers, the first one hides k, and the second one the message. • • • Decrypting: Dprivate−k(y 1, y 2) = y 2 · (y 1 a)-1(mod p) y 2 · (y 1 a)-1 = x · ¯k(qak)-1 = x · (qak)-1(mod p) = x Check example next slight.

El Gamal public-key cryptosystem • Example: – p = 43, q=3 primitive root of p, Alice’s choice of secret key is a=7, – ¯ = qa( mod p) = 37( mod 43) = 37, – Bob picks a random key k=26, and his message x=14, y 1= 326 = 15 mod(43), y 2= 3726 14 = 31 mod(43), – CT= {15, 43} large prime number, q- primitive root of p, made public. • Alice: 31 · (157)-1 = 14( mod 43). • El Gamal encryption is randomized, depends on random k. So the same x has many encryptions.

• • Authentication Server Based on the fact that there exists a trustworthy authentication server. The authentication server provides a secure way for pair of processes to obtain secret keys. Needham & Schroeder suggested two mechanisms to construct such a server: – Authentication with secret keys. – Authentication with public keys. • Kerberos is based on the secret-key method. • • • Secret Key Authentication A, B : the processes. S : the server N : a nonce K : a key. Only the server knows K and K • • • A S: A, B, Na S A: {Na, B, Kab, {Kab, A, timestamp}Kb}Ka A B: {Kab, A, timestamp}Kb B A: {Nb}Kab A B: {Nb-1}Kab

• Digital Signatures • Enable to verify that a message was originally produced by the signatory. • Enable to verify that a message content was not subsequently altered. • Handwritten signatures cannot entirely provide that. • Hard to detect forged signatures. • Hard to prevent alteration of the document. • Digital Signature with Public Key • For each message we add a signature which is constructed as follows: – Compute a digest function of the message (like hash function) to reduce length. – Encrypt the result using our private key. • The receiver – Deciphers the signature using our public key. – Computes the digest function on the document. – Compares the two to validate the document.