Cryptographic Program Obfuscation Craig Gentry IBM T J

Cryptographic Program Obfuscation Craig Gentry IBM T. J. Watson Research Center March 2017 Spring School on Lattice-Based Crypto, Oxford

Code Obfuscation Make programs “unintelligible” while maintaining their functionality Example from Wikipedia: @P=split//, ". URRUUc 8 R"; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p", "u$p"}=(P, P); pipe"r$p", "u$p"; ++$p; ($q*=2)+ =$f=!fork; map{$P=$P[$f^ord ($p{$_})&6]; $p{$_}=/ ^$P/ix? $P: close$_}keys%p}p; p; p; map{$p{$_}=~/^[P. ]/&& close$_}%p; wait until$? ; map{/^r/&&<$_>}%p; $_=$d[$q]; sleep rand(2)if/S/; print Why do it? How to define “unintelligible”? Can we achieve it?

Why Obfuscation? Hiding secrets in software Plaintext strutpatent. com AES encryption Ciphertext

Why Obfuscation? Hiding secrets in software Plaintext @P=split//, ". URRUUc 8 R"; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p", "u$p"}=(P, P); pipe"r$p", "u$p"; ++$p; ($q *=2)+=$f=!fork; map{$P=$P[$f^ord ($p{$_})&6]; $p{$_}=/ ^$P/ix? $P: close$_}keys%p}p; p; p; map{$p{$_} =~/^[P. ]/&& close$_}%p; wait until$? ; map{/^r/&&<$_>}%p; $_=$d[$q]; sleep rand(2)if/S/; print Ciphertext AES encryption Public-key encryption

Why Obfuscation? Hiding secrets in software Credentials Verify credentials Output data Data Put software components together

Why Obfuscation? Hiding secrets in software Credentials @P=split//, ". URRUUc 8 R"; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p", "u$p"}=(P, P); pipe"r$p", "u$p"; ++$p; ($q *=2)+=$f=!fork; map{$P=$P[$f^ord ($p{$_})&6]; $p{$_}=/ ^$P/ix? $P: close$_}keys%p}p; p; p; map{$p{$_} =~/^[P. ]/&& close$_}%p; wait until$? ; map{/^r/&&<$_>}%p; $_=$d[$q]; sleep rand(2)if/S/; print Data Put software components together … inseparably. Digital rights management (DRM)

Why Obfuscation? Hiding secrets in software http: //www. arco-iris. com/George/images/game_of_go. jpg Game of Go Next move Uploading my expertise to the web

Why Obfuscation? Hiding secrets in software Game of Go @P=split//, ". URRUUc 8 R"; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p", "u$p"}=(P, P); pipe"r$p", "u$p"; ++$p; ($q*=2)+= $f=!fork; map{$P=$P[$f^ord ($p{$_})&6]; $p{$_}=/ ^$P/ix? $P: close$_}keys%p}p; p; p; map{$p{$_}=~/^[P. ]/&& close$_}%p; wait until$? ; map{/^r/&&<$_>}%p; $_=$d[$q]; sleep rand(2)if/S/; print Next move Uploading my expertise to the web without revealing my strategies

Why Obfuscation? Hiding secrets in software What I see What I say My brain

Why Obfuscation? Hiding secrets in software What I see @P=split//, ". URRUUc 8 R"; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p", "u$p"}=(P, P); pipe"r$p", "u$p"; ++$p; ($q *=2)+=$f=!fork; map{$P=$P[$f^ord ($p{$_})&6]; $p{$_}=/ ^$P/ix? $P: close$_}keys%p}p; p; p; map{$p{$_} =~/^[P. ]/&& close$_}%p; wait until$? ; map{/^r/&&<$_>}%p; $_=$d[$q]; sleep rand(2)if/S/; print What I say My brain… made digital… securely!!!

Defining Obfuscation An obfuscator makes a program “unintelligible” while preserving its functionality. For all circuits (functions) C in some class C, obfuscator O is: Functionality preserving: O(C)(x) = C(x) for all inputs x Efficient: O(C)’s running time is polynomial in C’s “Unintelligible”: O(C) hard to analyze/reverse-engineer. Minimal requirement: One-wayness: Hard to recover C from O(C) Maximal requirement: O(C) is like a “black box” that evaluates C

Strong Black Box Obfuscation A natural formal interpretation For any efficient adversary A, there’s a simulator S, such that for any circuit C: A(O(C)) ≈C. I. SC(1|C|) What it means: A learns no more from O(C) than S does from oracle access to C. This definition is impossible to meet! If C is “unlearnable” (like a pseudorandom function), S cannot efficiently output a circuit C’ equivalent to C. A definitely learns something that S doesn’t.

Even Weak Black Box Obfuscation is Impossible! There are circuit families C that are unobfuscatable. Shh, hang on. I can hear something.

Indistinguishability Obfuscation (i. O) For any efficient adversary A, for any equal-length circuits C 1, C 2 that compute the same function: |Pr [A(O(C 1))=1] - Pr [A(O(C 2))=1]| is negligible. What it means: If two circuits compute same function, adversary cannot distinguish which was obfuscated. Also defined by Barak et al.

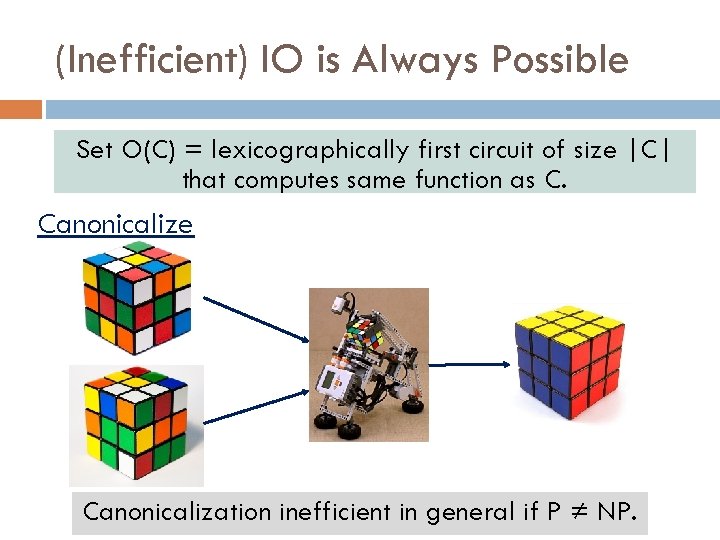
(Inefficient) IO is Always Possible Set O(C) = lexicographically first circuit of size |C| that computes same function as C. Canonicalize Canonicalization inefficient in general if P ≠ NP.

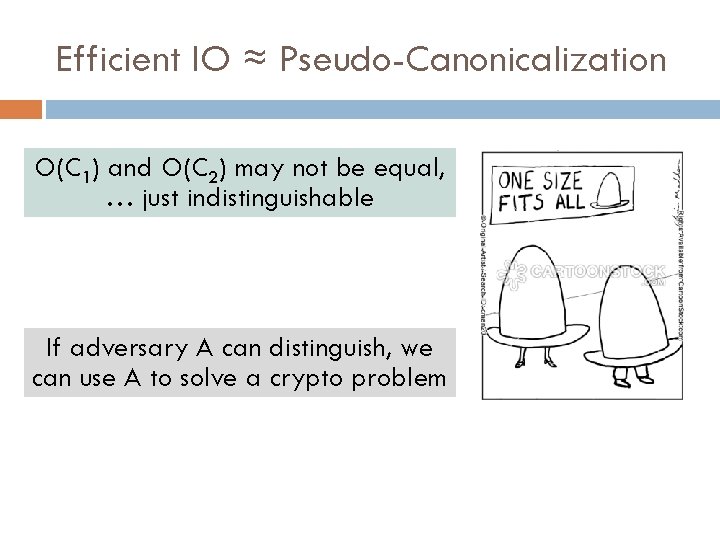
Efficient IO ≈ Pseudo-Canonicalization O(C 1) and O(C 2) may not be equal, … just indistinguishable If adversary A can distinguish, we can use A to solve a crypto problem

Limitation of IO Only promises to pseudo-canonicalize C Does not (necessarily) promise to hide C’s secrets

But IO is “Best-Possible” Obfuscation An indistinguishability obfuscator is “as good" as any other obfuscator that exists. [GR 07]

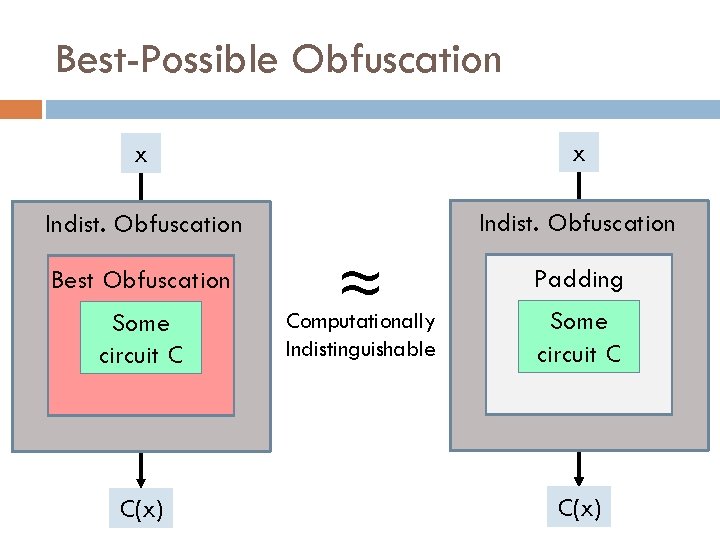
Best-Possible Obfuscation x x Indist. Obfuscation Best Obfuscation Some circuit C C(x) ≈ Computationally Indistinguishable Padding Some circuit C C(x)

Many Applications of IO OWFs+i. O → public key enc. [DH 76, GGHRSW 13, SW 13] Witness encryption: Encrypt x so only someone with proof of Riemann Hypothesis can decrypt [GGSW 13] Functional encryption: Noninteractive access control system where Dec(Key. Y, Enc(x)) → F(X, Y) [GGHRSW 13] Many more …

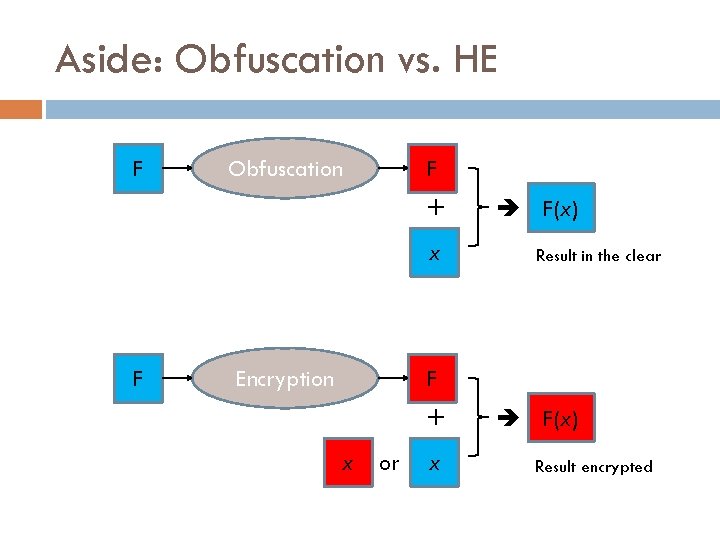
Aside: Obfuscation vs. HE F Obfuscation F + x F Encryption F(x) Result in the clear F + x or x F(x) Result encrypted

GGHRSW Obfuscation Construction Two Steps: Obfuscate NC 1 Circuits Uses branching programs (a la Barrington and Kilian) Encodes permutation matrices using “multilinear maps” Bootstrap obfuscation of NC 1 to obfuscation of P Simple provable transformation Uses FHE and statistically sound NIZKs

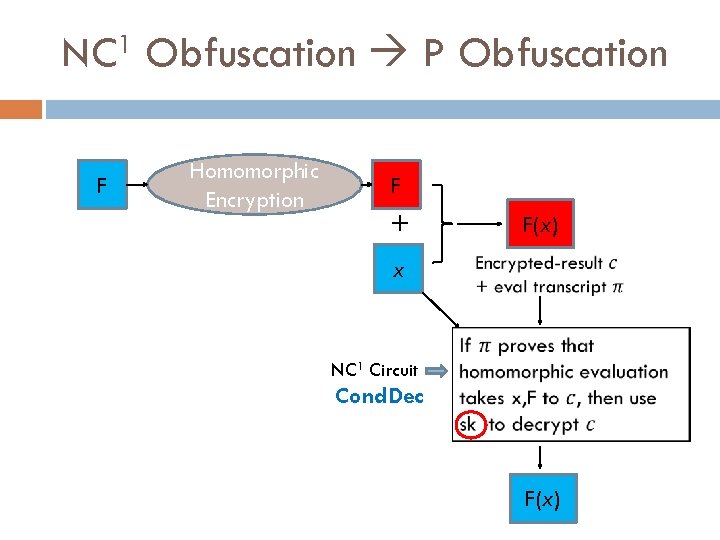
NC 1 Obfuscation P Obfuscation F Homomorphic Encryption F + F(x) x NC 1 Circuit Cond. Dec F(x)

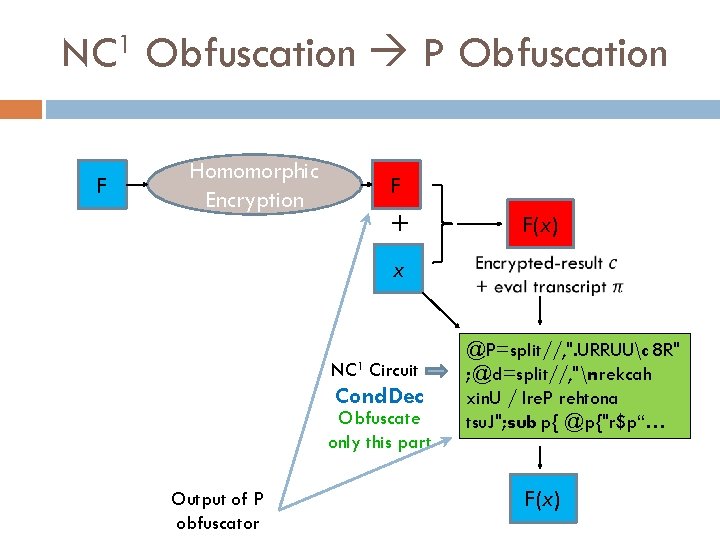
NC 1 Obfuscation P Obfuscation F Homomorphic Encryption F + x NC 1 Circuit Cond. Dec Obfuscate only this part Output of P obfuscator F(x) @P=split//, ". URRUUc 8 R" ; @d=split//, "nrekcah xin. U / lre. P rehtona tsu. J"; sub p{ @p{"r$p“… F(x)

Conditional Decryption with i. O We have i. O, not “perfect” obfuscation But we can adapt the Cond. Dec approach We use two HE secret keys

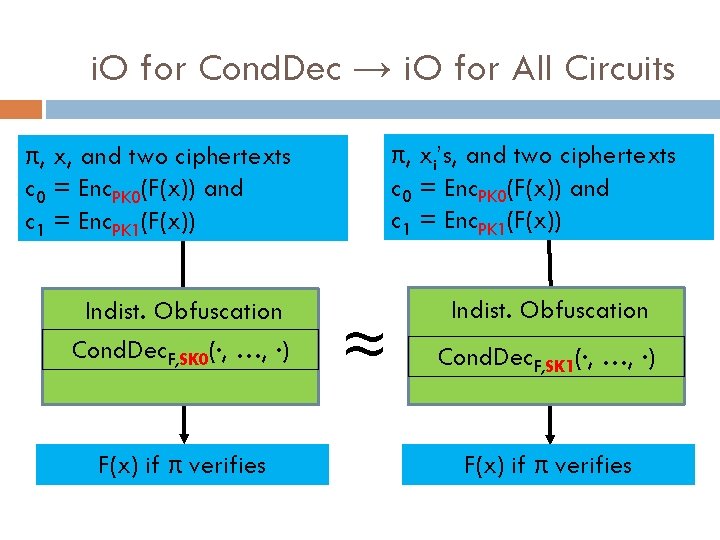
i. O for Cond. Dec → i. O for All Circuits π, xi’s, and two ciphertexts c 0 = Enc. PK 0(F(x)) and c 1 = Enc. PK 1(F(x)) π, x, and two ciphertexts c 0 = Enc. PK 0(F(x)) and c 1 = Enc. PK 1(F(x)) Indist. Obfuscation Cond. Dec. F, SK 0(·, …, ·) F(x) if π verifies ≈ Indist. Obfuscation Cond. Dec. F, SK 1(·, …, ·) F(x) if π verifies

Analysis of Two-Key Technique 1 st program has secret SK 0 inside (but not SK 1). 2 nd program has secret SK 1 inside (but not SK 0). But programs are indistinguishable So, neither program “leaks” either secret. Two-key trick is very handy in i. O context. Similar to Naor-Yung ’ 90 technique to get encryption with chosen ciphertext security

i. O for NC 1 Construction Complicated… Also, not very efficient… Also, security is iffy… Main ingredient: Cryptographic multilinear maps

Multilinear Map Schemes

What is a cryptographic mmap? An FHE scheme that leaks. Zero test: Anyone can distinguish when 0 is encrypted.

Why would you do that? FHE is awesome (of course): I give the cloud encrypted program E(P) For (possibly encrypted) x, cloud can compute E(P(x)) I can decrypt to recover P(x) Cloud learns nothing about P, or even P(x) But it has a shortcoming… What if I want the cloud to learn P(x) (but still not P)? So that the cloud can take some action if P(x) = 1. Cryptographic mmaps can be positioned to “leak” a ‘ 0’ precisely when some condition is satisfied.

Mmaps from Homomorphic NTRU [GGH 13] NTRU ctext that encrypts m at “level d” has form e/s d. e is small, e = m mod p s is the secret key To decrypt, multiply by sd and reduce mod p. Given level-d encodings c 1 = e 1/sd and c 2 = e 2/sd, how do we test whether they encode the same m? If they encode same thing, then e 1 -e 2 = 0 mod p. Moreover, (e 1 -e 2)/p is a “small” polynomial.

Adding a Zero/Equality Test to NTRU Zero-Testing parameter: z = h∙sd/p for “medium-size” h (e. g. |h| ≈ q 3/4) z(c 1 -c 2) = h(e 1 -e 2)/p If c 1, c 2 encode same thing, |h(e 1 -e 2)/p| is “medium-sized” Otherwise, denominator p hopefully makes result look random mod q (when p is a polynomial, not a scalar).

Aren’t Mmap Schemes Broken? Yes and no. Key agreement: Broken! All attempts to get multipartite key agreement “naturally” from mmaps are broken. Obfuscation: Not broken! Since obfuscation is all-powerful, you can even get multipartite KA from it “unnaturally”.

Two “Modes” of Using MMAPS The Mathematics of Modern Cryptography Private Encoding vs. Public Encoding requires trapdoor Modeled as “Multilinear Jigsaw Puzzles” [GGHRSW 13] Sufficient for many/most obfuscation schemes Largely untouched by known attacks Encoding/re-randomization is available to anyone Via public encoding of zero Needed for key-agreement, some hardness assumptions Current mmaps are broken when used in this mode

The Future of Obfuscation and MMaps A bumpy ride… My guess: Variants of current obfuscation schemes will remain unbroken. But we need better schemes: More practical Reducible to nice computational assumptions Ideally, noise-free!

Thank You! Questions? E D M T I I RE P X E ?