Cryptographic Primitives Implemented Efficiently Correctly and Securely Nik

Cryptographic Primitives Implemented Efficiently, Correctly and Securely Nik Swamy, OPLSS 2021 Thanks to Jonathan Protzenko and Chris Hawblitzel for these slides. Errors are mine

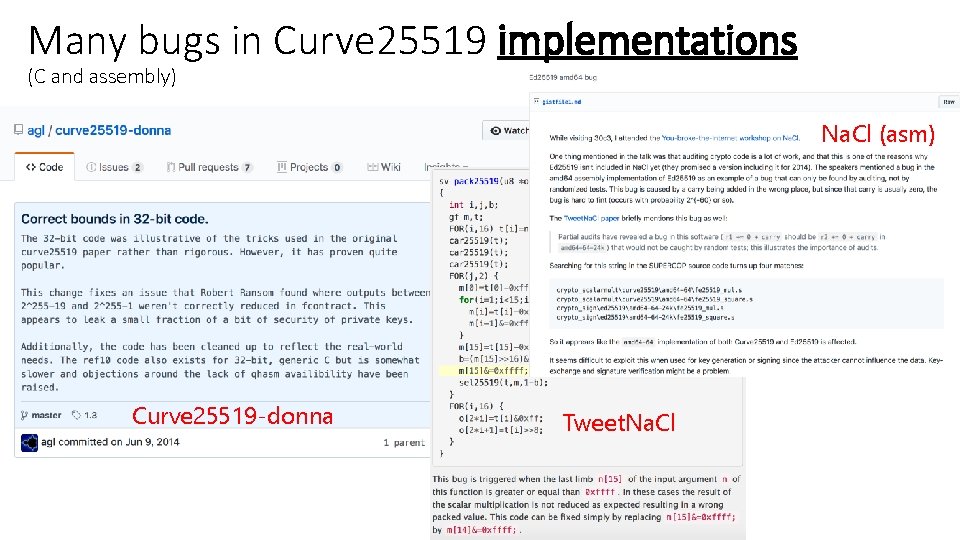
Many bugs in Curve 25519 implementations (C and assembly) Na. Cl (asm) Curve 25519 -donna Tweet. Na. Cl

3 Bugs in Open. SSL implementation of Poly 1305 Low* 4

Implementation bug in AES-GCM

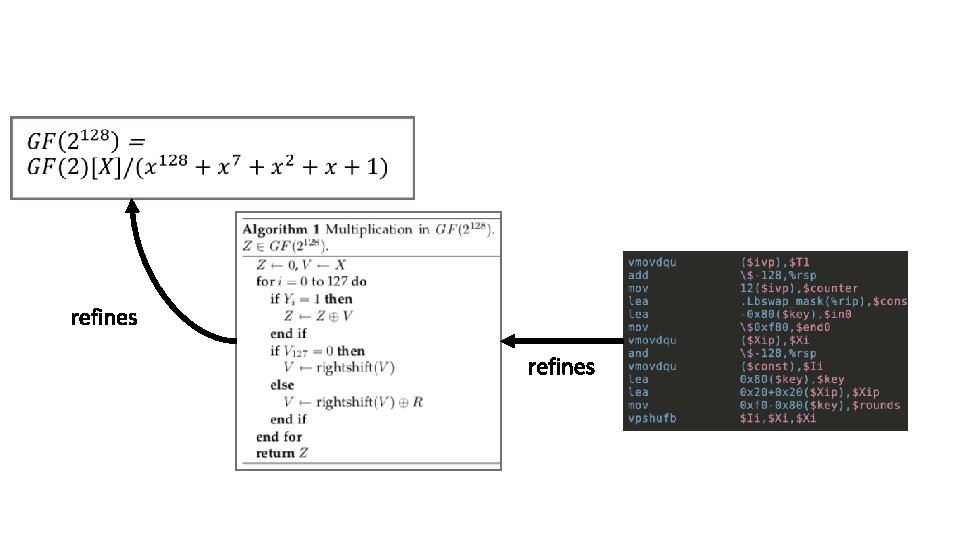
AES-GCM “the math”

Distilling the math for implementors “the algorithm”

Writing the actual code “the reality”

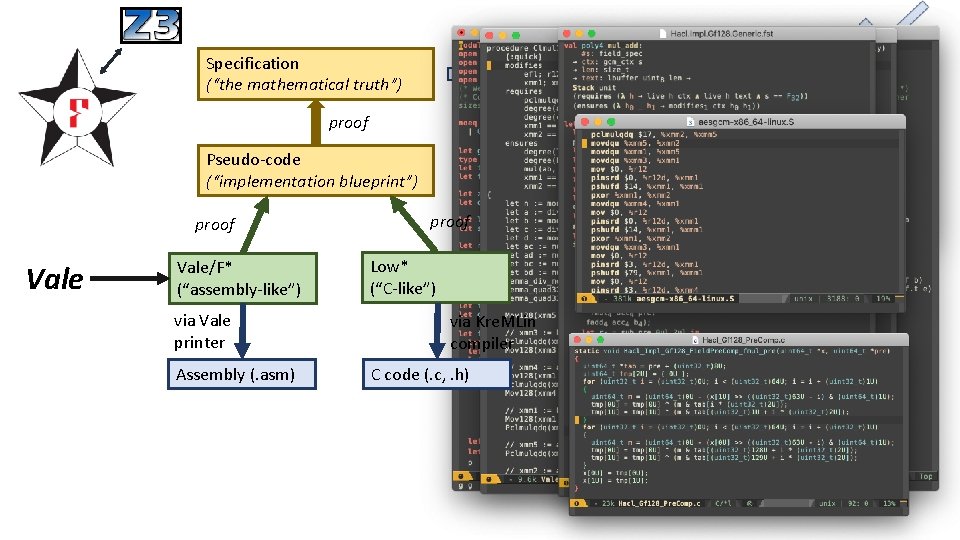
Verified Assembly Language in Vale / F*

Specification (“the mathematical truth”) via ocaml proof Pseudo-code (“implementation blueprint”) proof Vale/F* (“assembly-like”) via Vale printer Assembly (. asm) proof Low* (“C-like”) via Kre. MLin compiler C code (. c, . h) spec-test. exe (“testable specification”)

What do we verify? Memory- and type-safety. Mitigates buffer overruns, dangling pointers, code injections. No undefined behavior. Our fast implementations behave precisely as our simpler specifications. Access to secrets, including crypto keys and private app data is restricted according to design. Each application can do custom proofs beyond functional correctness and safety: - non malleability (parsers) - crypto games (TLS) - security reduction (Merkle Trees) - etc.

We have a fast verified AES-GCM

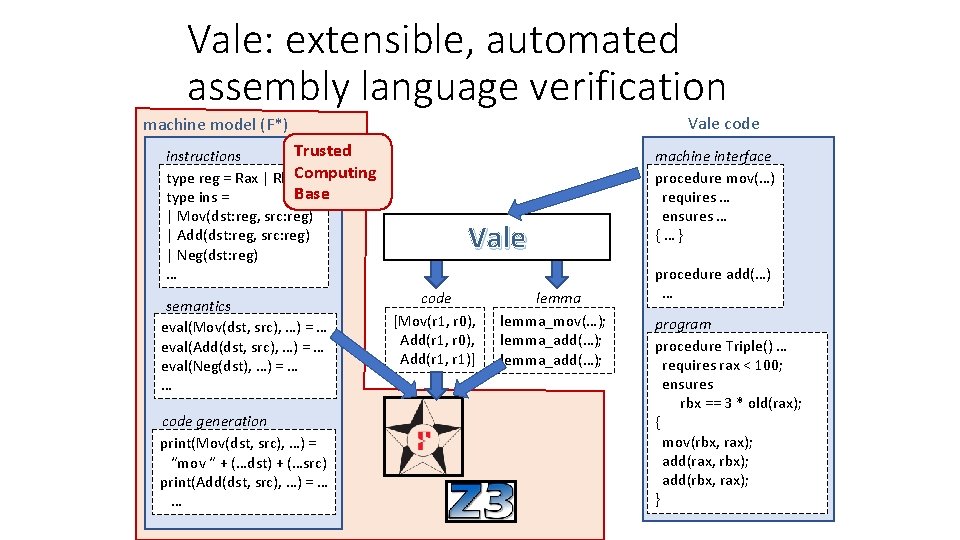
Vale: extensible, automated assembly language verification Vale code machine model (F*) Trusted instructions Computing type reg = Rax | Rbx|. . . Base type ins = | Mov(dst: reg, src: reg) | Add(dst: reg, src: reg) | Neg(dst: reg) … semantics eval(Mov(dst, src), …) = … eval(Add(dst, src), …) = … eval(Neg(dst), …) = … … code generation print(Mov(dst, src), …) = “mov “ + (…dst) + (…src) print(Add(dst, src), …) = … … Vale code [Mov(r 1, r 0), Add(r 1, r 1)] lemma_mov(…); lemma_add(…); machine interface procedure mov(…) requires … ensures … {…} procedure add(…) … program procedure Triple() … requires rax < 100; ensures rbx == 3 * old(rax); { mov(rbx, rax); add(rax, rbx); add(rbx, rax); }

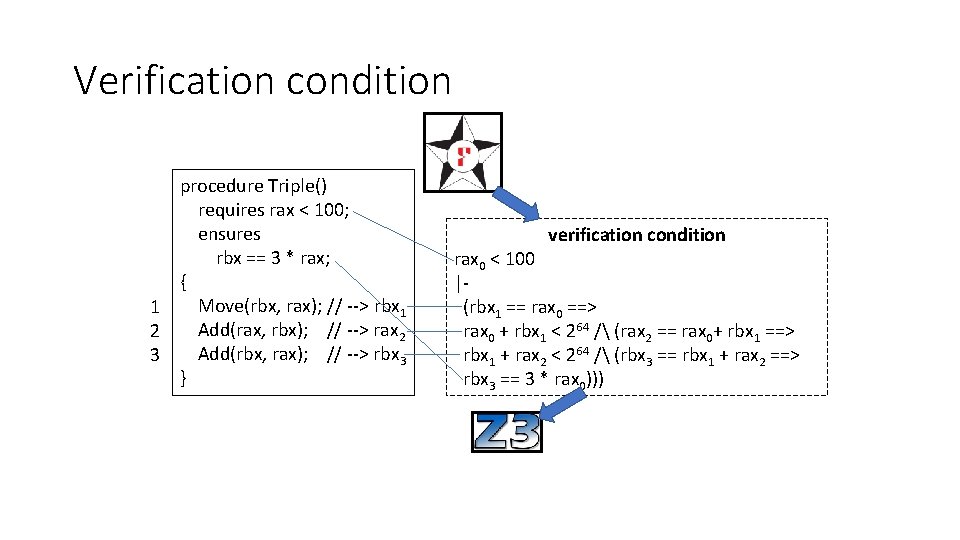
Verification condition procedure Triple() requires rax < 100; ensures rbx == 3 * rax; { Move(rbx, rax); // --> rbx 1 1 Add(rax, rbx); // --> rax 2 2 Add(rbx, rax); // --> rbx 3 3 } verification condition rax 0 < 100 |(rbx 1 == rax 0 ==> rax 0 + rbx 1 < 264 / (rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 / (rbx 3 == rbx 1 + rax 2 ==> rbx 3 == 3 * rax 0)))

Demo • Verification condition generation for Vale

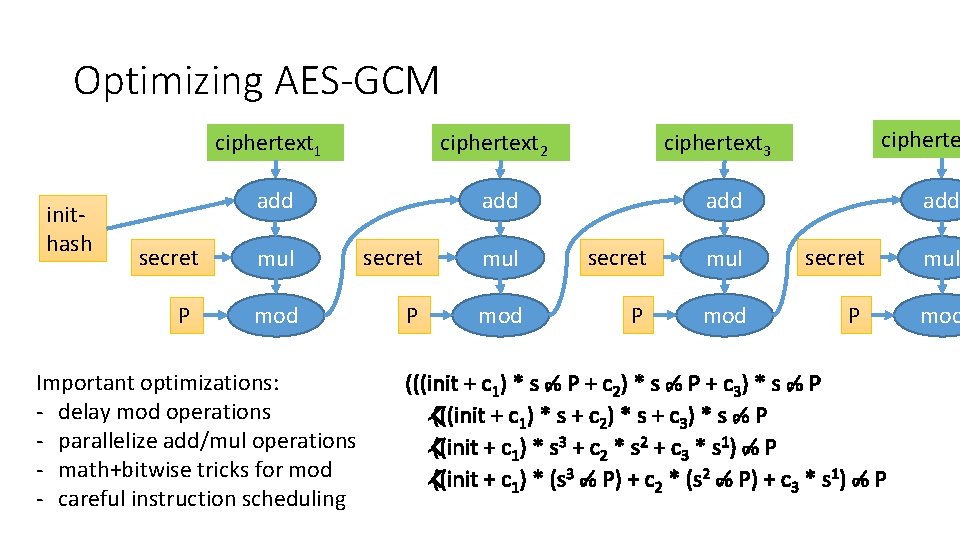
Optimizing AES-GCM inithash secret P ciphertext 1 ciphertext 2 ciphertext 3 add add cipherte add mul secret mul mod P mod Important optimizations: - delay mod operations - parallelize add/mul operations - math+bitwise tricks for mod - careful instruction scheduling

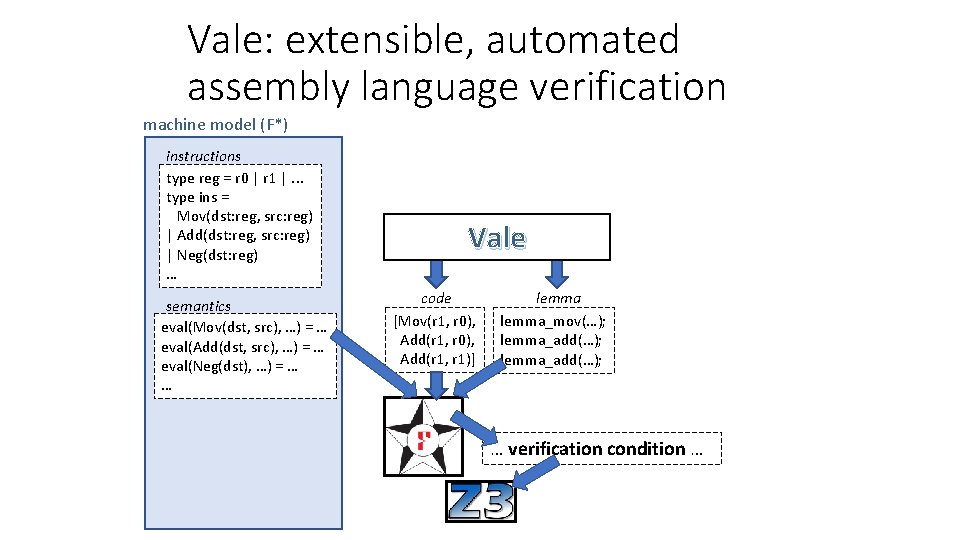
Vale: extensible, automated assembly language verification machine model (F*) instructions type reg = r 0 | r 1 |. . . type ins = Mov(dst: reg, src: reg) | Add(dst: reg, src: reg) | Neg(dst: reg) … semantics eval(Mov(dst, src), …) = … eval(Add(dst, src), …) = … eval(Neg(dst), …) = … … Vale code [Mov(r 1, r 0), Add(r 1, r 1)] lemma_mov(…); lemma_add(…); … verification condition …

Ugh! Default SMT query looks awful! verification condition we want: ……………. (rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 …………………. verification condition we get: … (forall (ghost_result_0: (state * fuel)). (let (s 3, fc 3) = ghost_result_0 in eval_code (Ins (Add 64 (OReg (Rax)) (OReg (Rbx)))) fc 3 s 2 == Some s 3 / eval_operand (OReg Rax) s 3 == eval_operand (OReg Rax) s 2 + eval_operand (OReg Rbx) s 2 / s 3 == update_state (OReg Rax). r s 3 s 2) ==> lemma_Add s 2 (OReg Rax) (OReg Rbx) == ghost_result_0 ==> (forall (s 3: state) (fc 3: fuel). lemma_Add s 2 (OReg Rax) (OReg Rbx) == Mktuple 2 s 3 fc 3 ==> Cons? codes_Triple. tl / (forall (any_result 0: list code). codes_Triple. tl == any_result 0 ==> (forall (any_result 1: list code). codes_Triple. tl == any_result 1 ==> OReg? (OReg Rbx) / eval_operand (OReg Rbx) s 3 + eval_operand (OReg Rax) s 3 < 264. . .

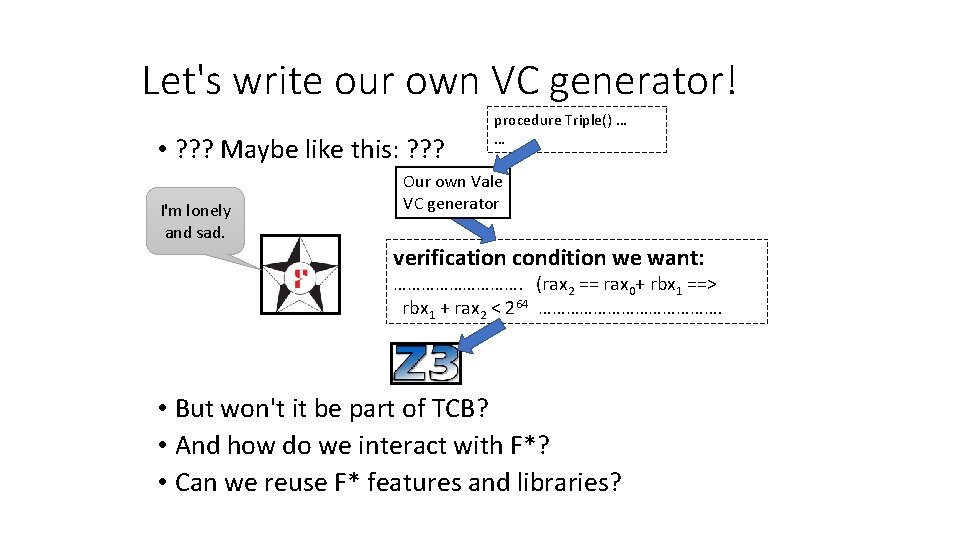
Let's write our own VC generator! • ? ? ? Maybe like this: ? ? ? I'm lonely and sad. procedure Triple() … … Our own Vale VC generator verification condition we want: ……………. (rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 …………………. • But won't it be part of TCB? • And how do we interact with F*? • Can we reuse F* features and libraries?

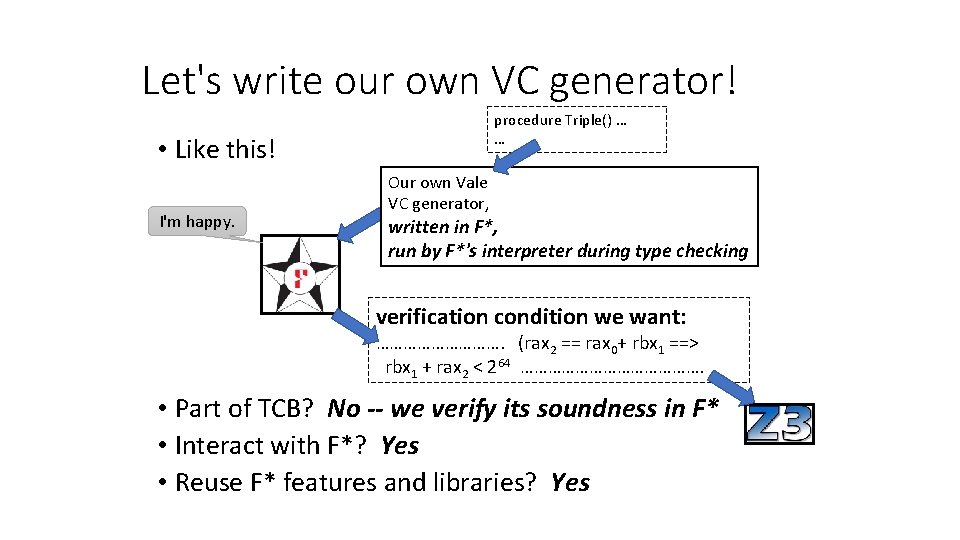
Let's write our own VC generator! procedure Triple() … … • Like this! I'm happy. Our own Vale VC generator, written in F*, run by F*'s interpreter during type checking verification condition we want: ……………. (rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 …………………. • Part of TCB? No -- we verify its soundness in F* • Interact with F*? Yes • Reuse F* features and libraries? Yes

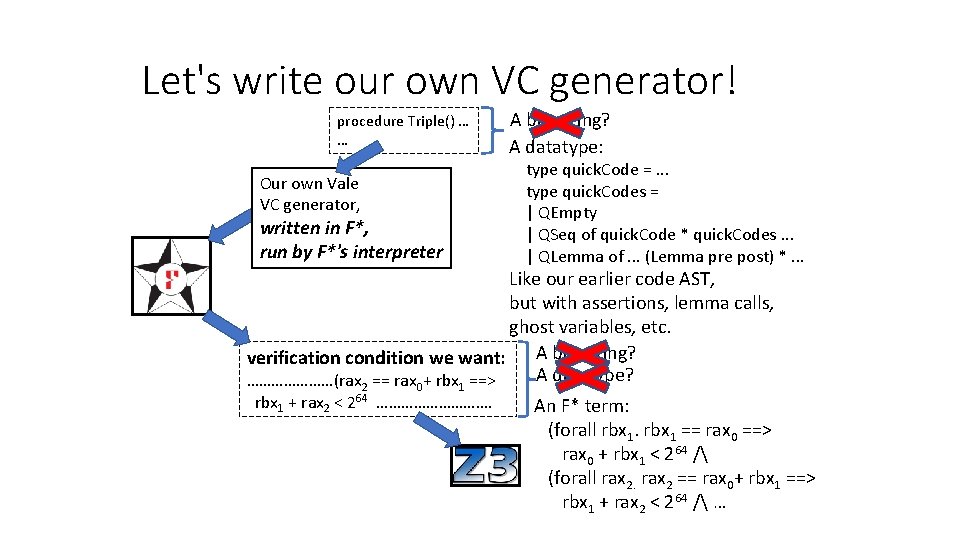
Let's write our own VC generator! procedure Triple() … … Our own Vale VC generator, written in F*, run by F*'s interpreter A big string? A datatype: type quick. Code =. . . type quick. Codes = | QEmpty | QSeq of quick. Code * quick. Codes. . . | QLemma of. . . (Lemma pre post) *. . . Like our earlier code AST, but with assertions, lemma calls, ghost variables, etc. A big string? verification condition we want: A datatype? …………………(rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 ……………. An F* term: (forall rbx 1 == rax 0 ==> rax 0 + rbx 1 < 264 / (forall rax 2 == rax 0+ rbx 1 ==> rbx 1 + rax 2 < 264 / …