Cryptanalysis of Short Exponent RSA with Primes Sharing

Cryptanalysis of Short Exponent RSA with Primes Sharing Least Significant Bits Hung-Min Sun, Mu-En Wu Department of Computer Science, National Tsing Hua University, Taiwan Ron Steinfeld Centre for Advanced Computing - Algorithms and Cryptography, Department of Computing, Macquarie University, Australia Jian Guo, Huaxiong Wang School of Physical and Mathematical Science, Nanyang Technological University, Singapore Date: 2008/12/02

Outline l LSBS RSA l Lattice Reduction Technique l Zhao-Qi Attack l Our Improvement l Comparison and Experiment l Conclusion and Future Work

LSBS-RSA l An RSA system with modulus primes sharing a large number of least significant bits (LSBs). l l Ex: 512 bit p and 512 bit q share 64 LSBs p: 1010100111100…. . … 011 q: 111010101010…. . … 011 Why use LSBS-RSA? l l Benefit: Improve the efficiency of a server aided RSA signature (SASG) However, how about the security consideration?

Notation l Notation (α, β, γ) l α: |p – q| = r．2(1/2 - α)n for some odd integer r. l l β: d = Nβ γ: e = Nγ p: q: (1/2 - α)n

A property of LSBS-RSA If p: q: Then, the part p + q: a a } Unknown, but the same will appear and 2 a LSBs of p + q is known. 2 a bits Known

Lattice Reduction Technique

Lattice Attack Using lattice reduction technique we can solve the modular multivariate equation l Using lattice to l l l find the small root of modular polynomials EX: f(x, y) = ax +by +c mod Z with root (x 0, y 0, z 0), where x 0<X, y 0<Y, z 0<Z. We may regard f as the coefficient vector (a, b, c) and construct the other polynomials fi with the same small root (x 0, y 0, z 0). Using lattice reduction technique to find the polynomial without modulo and then find out the small root (x 0, y 0, z 0).

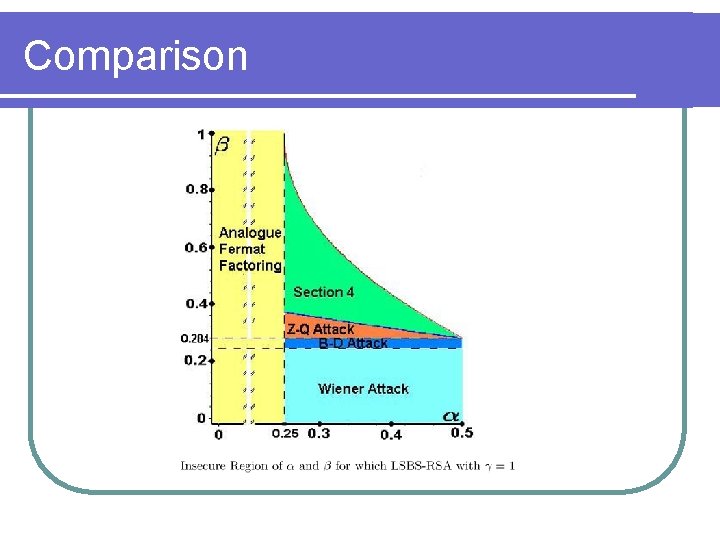
Lattice reduction technique Boneh and Durfee first use this technique to prove that RSA with d<N 0. 292 is insecure. l Zhao and Qi extended their attack to LSBS-RSA and got the following result: l l Applying α=1/2 yields the same result of Boneh and Durfee’s attack.

The Zhao-Qi Attack ed = k[(N+1)-(p+q)]+1 l ed = k[(N+1)-2 q- r．2(1/2 - α) )]+1 l l Let A=N+1, a= 2(1/2 - α) Let x 0=k, y 0=q, and z 0=r Then, (x 0, y 0, z 0) is a root of l l f(x, y, z)=x(A-2 y-az)+1 (mod e) with the bounds |x 0|<X=Nγ+β-1 |y 0|<Y=N 1/2 |z 0|<X=Nα

Our Improvement l f(x, y, z)=x(A-2 y-az)+1 (mod e) with the bounds l l l |x 0|<X=Nγ+β-1 |y 0|<Y=N 1/2 |z 0|<X=Nα ed = k[(N+1)-(p+q)]+1 l f*(x, y, z)=x(B-by)+1 (mod e) l l l where B = N+1 -φ0, b=2(1 -2α)n Consider f(x, y, z)=xy+B’x+C’ (mod e) l After multiplying B-1 to f*

Our Improvement l Consider l Then, the polynomials construct the coefficient matrix

The case m=3, t=1

Conti. . l We have to set det(Mx)．det(My) <emw, where w is the dimension of the matrix. l Note thatdet(Mx)<emw implies the result of the Wiener attack.

l det(Mx)．det(My) <emw implies our result:

Comparison

Experiment

Conclusion and Future work We extend the Boneh-Durfee attack to the general case by considering the prime sharing LSBs. l How about the case of prime sharing LSBs and MSBs simultaneously l In order to enhance the efficiency of the operation, how to design LSBS-RSA with short public exponent and private exponent? l

l Thanks l for your attention!! Any question please contact to mn@is. cs. nthu. edu. tw