Cryptanalysis Kyle Johnson Cryptology Comprised of both Cryptography

Cryptanalysis Kyle Johnson

Cryptology �Comprised of both Cryptography and Cryptanalysis �Cryptography - which is the practice and study of techniques for secure communication in the presence of third parties �Cryptanalysis - which is the art of defeating cryptographic security systems, and gaining access to the contents of encrypted messages or obtaining the key itself.

History • Fialka Cipher machine • Used by the Soviet in the cold war era. • Uses 10 rotors each with 30 contacts and also makes use of a punch card mechanism. http: //en. wikipedia. org/wiki/File: FIALKA-rotors-in-machine. jpg

Cryptanalysis Tools Scytale(rhymes with Italy) Ancient Greek device used to implement a cipher. Vigenere square used for the Vigenere Cipher. http: //www. braingle. com/brainteasers/codes/images/scytale. gif http: //en. wikipedia. org/wiki/File: Vigen%C 3%A 8 re_square_shading. svg

Classical Ciphers �Term given by William Friedman in 1920 �First recorded explanation in the 9 th century by Al. Kindi �A manuscript �Blaise de Vigenere used a repeating key cipher

Significance in History �Mary, Queen of Scots �World War I, Zimmerman Telegram �World War II, German Enigma Machine

Cryptanalysis Results (Breaks) �Total Break �Global deduction �Instance (local) deduction �Information Deduction �Distinguishing algorithm

Types of Attacks �Ciphertext-only �Known-plaintext �Chosen-Ciphertext

Ciphertext-only �Also known as the known-ciphertext attack �Attacker only has a set of Ciphertexts �Successful, plaintext or key obtained �Used in Frequency Analysis

Known-plaintext �Attacker has both the plaintext and ciphertext. �Goal: get the key �WWII: German Enigma Machine �Length, patterns, frequency

Known-Plaintext Example � Plaintext: “THIS IS AN EXAMPLE OF A CIPHER” � Ciphertext: “XLMW MW ER IBEQTPI SJ E GMTLIV” � Try Caesar Cipher: word length pattern noticed. � Shift-1 Plaintext: “UIJT JT BO FYBNQMF PG B DJQIFS” � Ciphertext: “XLMW MW ER IBEQTPI SJ E GMTLIV” � Not the same. Repeat for all possible shifts(25 times) � Shift -4 Plaintext: “XLMW MW ER IBEQTPI SJ E GMTLIV” � Ciphertext: “XLMW MW ER IBEQTPI SJ E GMTLIV” � Same! � Caesar cipher: key is shift of 4.

Chosen-Plaintext �Choose Plaintext to get random ciphertext �Goal: Weaken the security, get key �Plaintext injections �Types of chosen-plaintext �Batch chosen-plaintext �Adaptive chosen-plaintext

Batch Chosen-plaintext Attack �Chooses all of the plaintexts before they are encrypted �This is the means of an unqualified use of this type of attack on encrypted data.

Adaptive Chosen-plaintext Attack �Attacker will make a series of interactive queries �Choosing subsequent plaintexts based on the information from the previous encryptions

Chosen Ciphertext �Choose ciphertext, decrypt unknown key �Enter multiple ciphertexts �May be both adaptive and non-adaptive �Types of chosen-ciphertext �Lunchtime Attack �Adaptive chosen ciphertext

Lunchtime Attack �Also known as the midnight or indifferent attack �Attacker makes adaptive chosen-ciphertext queries up to a certain point �Can attack computer while user at lunch.

Adaptive chosen-ciphertext �Attack in which ciphertexts may be chosen adaptively and after a challenge ciphertext is given to the attacker �Ciphertext can’t be used itself �Stronger attack than lunchtime but few practical attacks are of this form

Tests and Analysis �Frequency Analysis �Index of Coincidence �Kasiski Test

Frequency Analysis �Frequency of letters �Used to solve classical ciphers �Substitution �Caesar �Natural Langauge properties and patterns

Example of Frequency Analysis �Consider this ciphertext : � “XZJZ WI RN ZDCQLSZ MO R OJZKGZNYB RNRSBIWI”

Example of Frequency Analysis � “XZJZ WI RN ZDCQLSZ MO R OJZKGZNYB RNRSBIWI” � A: 0 � B: 2 � C: 1 � So on down the alphabet…

Example of Frequency Analysis � “XZJZ WI RN ZDCQLSZ MO R OJZKGZNYB RNRSBIWI” Frequency 8 6 4 Freq. 2 0 A B C D E F G H I J K L MNO P Q R S T U VWX Y Z

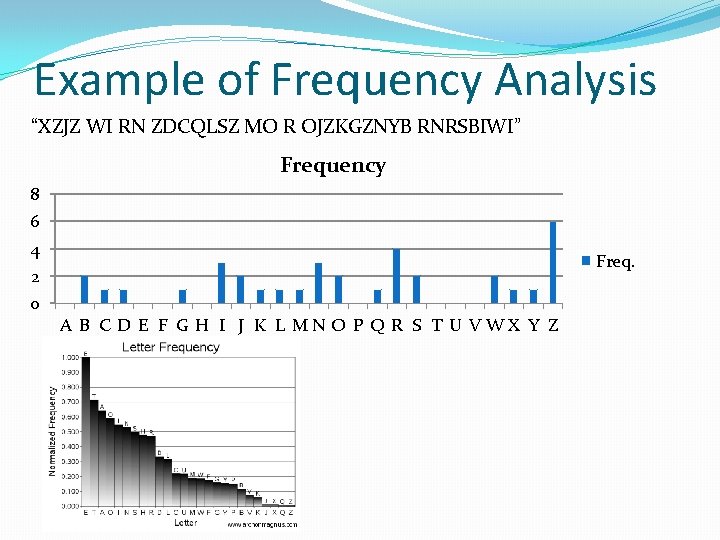
Example of Frequency Analysis “XZJZ WI RN ZDCQLSZ MO R OJZKGZNYB RNRSBIWI” Frequency 8 6 4 Freq. 2 0 A B C D E F G H I J K L MN O P Q R S T U VWX Y Z

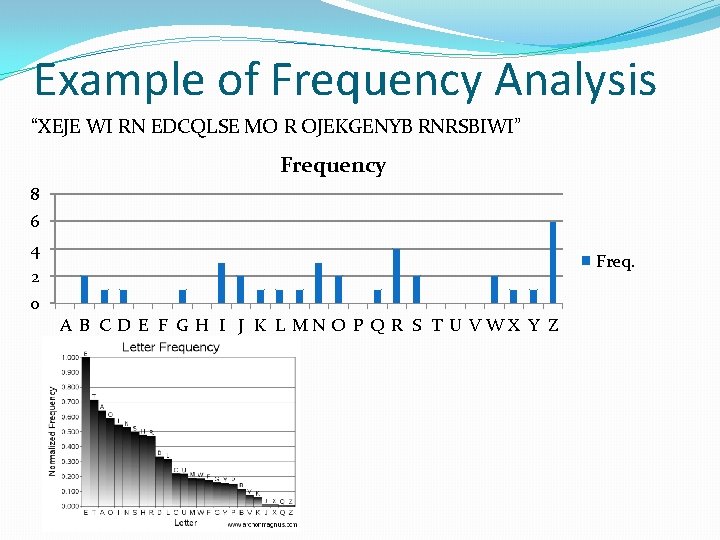
Example of Frequency Analysis “XEJE WI RN EDCQLSE MO R OJEKGENYB RNRSBIWI” Frequency 8 6 4 Freq. 2 0 A B C D E F G H I J K L MN O P Q R S T U VWX Y Z

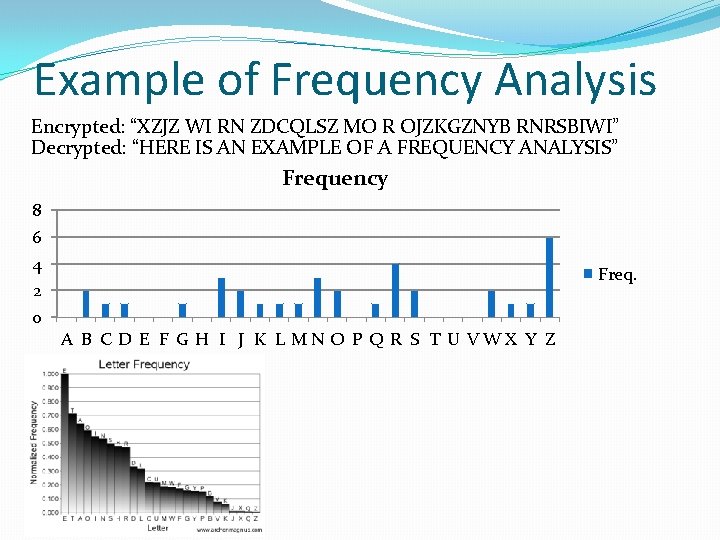
Example of Frequency Analysis Encrypted: “XZJZ WI RN ZDCQLSZ MO R OJZKGZNYB RNRSBIWI” Decrypted: “HERE IS AN EXAMPLE OF A FREQUENCY ANALYSIS” Frequency 8 6 4 2 0 Freq. A B C D E F G H I J K L MN O P Q R S T U VWX Y Z

Kasiski Test �Method of attacking polyalphabetic substitution ciphers �Deduce length of Keyword �‘m’ number of rows �Identical Segments of Ciphertext, length >= 3

Kasiski Test � Consider the following text: � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDD KOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQ KYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRLSV SKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMVGKMITZ HFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWXC VYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLA CNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTK HJVNPIST

Kasiski Test � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDD KOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQ KYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRLSV SKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMVGKMITZ HFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWXC VYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLA CNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTK HJVNPIST � Trigram HJV

Kasiski Test � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDD KOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQ KYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRLSV SKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMVGKMITZ HFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWXC VYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLA CNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTK HJVNPIST � Trigram HJV : differences (δ) = 18, 138, 54, 12

Kasiski Test � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDD KOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQ KYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRLSV SKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMVGKMITZ HFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWXC VYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLA CNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTK HJVNPIST � Trigram HJV : differences (δ) = 18, 138, 54, 12 � Greatest common denominator: m = 6 , length of the keyword is 6.

Index of Coincidence �Comparing 2 partials of same ciphertext �Ciphertext coincidences same in Plain Text �Used to help solve Vigenere cipher. �Check if two texts are in the same language, dialect

Index of Coincidence � Consider the text from the Kasiski Test: � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDDKOTFMBPVGEGL TGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQKYVXCHKFTPONCQQRHJVAJUW ETMCMSPKQDYHJVDAHCTRLSVSKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAH KJRJUMVGKMITZHFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWX CVYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLACNVRWBBIREP BBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTKHJVNPIST � And the length of the keyword m = 6

Index of Coincidence � KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUDDKOTFMBPVGEGL TGCKQRACQCWDNAWCRXIZAKFTLEWRPTYCQKYVXCHKFTPONCQQRHJVAJUW ETMCMSPKQDYHJVDAHCTRLSVSKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAH KJRJUMVGKMITZHFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFSPEZQNRWX CVYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHIFFSQESVYCLACNVRWBBIREP BBVFEXOSCDYGZWPFDTKFQIYCWHJVLNHIQIBTKHJVNPIST � And the length of the keyword m = 6 � Index of coincidence requires one to break the ciphertext up into the m number of rows. Each with as similar number of letters as possible.

Index of Coincidence �

Smaller example: Io. C �

Smaller example: Io. C �

Index of Coincidence �For English text the index of coincidences is approximately. o 66 �The index of coincidence for the previous example: � m = 1: 0. 041 � m = 2: 0. 038, 0. 047 � m = 3: 0. 056, 0. 048 � m = 4: 0. 037, 0. 042, 0. 037, 0. 050 � m = 5: 0. 043, 0. 031, 0. 035, 0. 043 � m = 6: 0. 063, 0. 084, 0. 049, 0. 065, 0. 042, 0. 071 � m = 7: 0. 031, 0. 044, 0. 043, 0. 038, 0. 044, 0. 041 �Since the values are closest to. 066 where m = 6 it is the appropriate choice for the keyword length.

Other attacks �Brute-Force Attack �Boomerang Attack �Linear cryptanalysis

Attack runtimes �

Today’s Cryptanalysis �The NSA has developed, due to an enormous breakthrough, the ability to cryptanalyze unfathomably complex encryption systems �This includes those developed by other governments but as well as average computer users in the US �The NSA is known for its mathematical breakthroughs in cryptanalysis especially differential cryptanalysis

Questions?