Cruising the Hypothesis Space Information Geometry with pictures

Cruising the Hypothesis Space: Information Geometry ( with pictures ) By SUNY at Albany Carlos C. Rodriguez Dept. of Mathematics The University at Albany carlos@math. albany. edu

• One Geometry? • Infinity

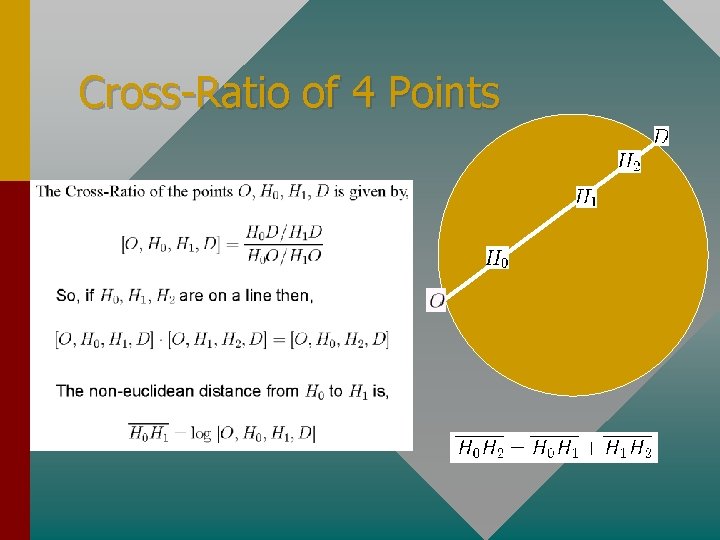
Cross-Ratio of 4 Points

Klein’s Erlanger Programme

The Theorem Between Theories and Things • Data, D (facts or things) • Hypothesis, H (theories) • Prior info, O (the rest)

Likelihood Ratio is a Cross-Ratio!

Information Geometry ? Omega. albany. edu: 8008/

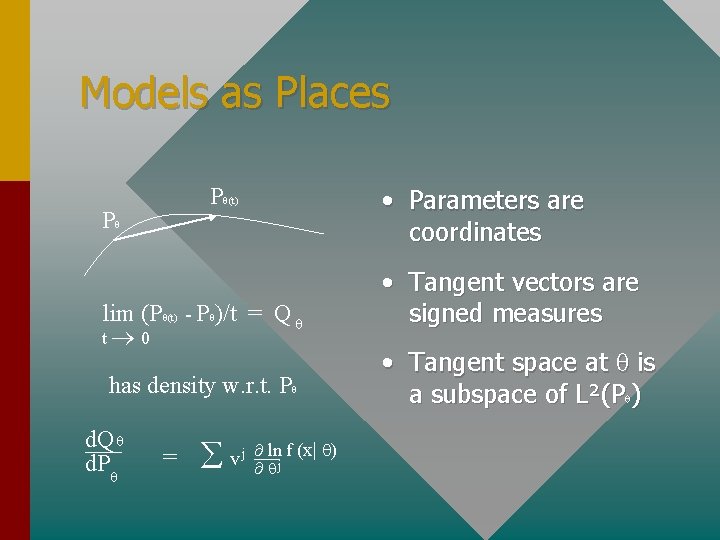
Models as Places P (t) P lim (P (t) - P )/t = Q t® 0 has density w. r. t. P d. Q d. P = å v j ¶¶¾ln j f (x| ) • Parameters are coordinates • Tangent vectors are signed measures • Tangent space at is a subspace of L²(P )

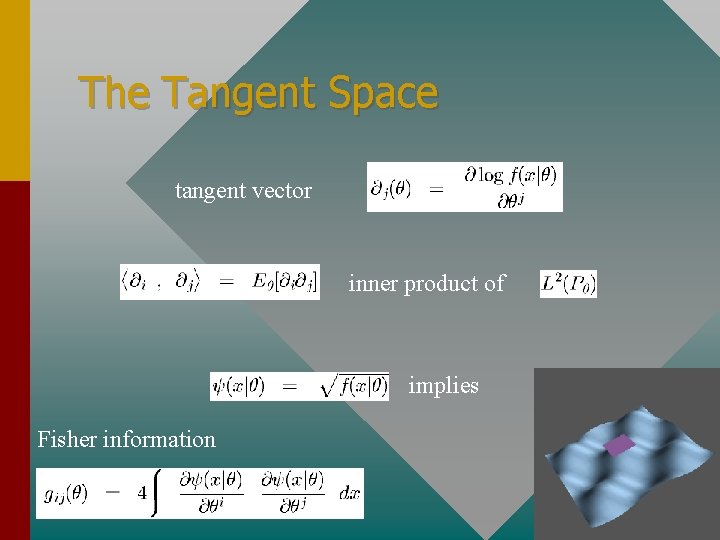
The Tangent Space tangent vector inner product of implies Fisher information

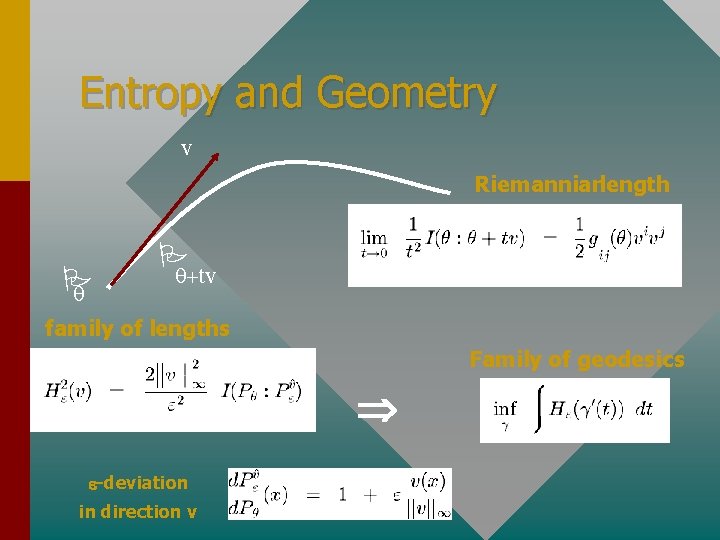
Entropy and Geometry v Riemannianlength +tv family of lengths Family of geodesics Þ e-deviation in direction v

Entropy and Ignorance • Let • Then • produces the family of entropicpriors • volume element Jeffreysprior

Entropy and Time

Radially Symmetric Distributions • ¥ dimensional manifold • location parameter • scale parameter s • shape parameter y • For fix y • curvature -1/J(y)

Uncertain Spinning Space Let e be radially symmetric about 0 and let i be the pseudo-scalar of 3 -space. Then y = + ie Represents a location + an uncertain degree of orientation or spinning with direction and magnitude given by i is a constant of magnitude 1. • E(y) = i commutes with everything. i is an oriented unit volume. i ²= -1 • E(y²) = ² - s² e

Spacetime as the Hypothesis Space of Radially Symmetric Distributions • Time is a consequence of uncertain space. • Space is ¥ dim and only on the average appears as 4 dim spacetime • Spin is a property of space so all fundamental particles must have spin

Curvature and Information Mass-Energy curves spacetime Prior information curves hypothesis spaces

In Closing. . . • Hypothesis spaces are cruisable. • Evidence is accumulating that statistical inference may include GR. And, there is a lot to be done: • The role of curvature in statistics. • A new approach to Quantum Gravity. SUNY at Albany