Crossover Trials Design and Analysis Peter T Donnan

Crossover Trials: Design and Analysis Peter T. Donnan Professor of Epidemiology and Biostatistics

Objectives of session • Understand what is meant by a • • • crossover trial design Understand the correlated nature of data Able to implement crossover analysis with continuous outcome in SPSS and SAS Interpret the output

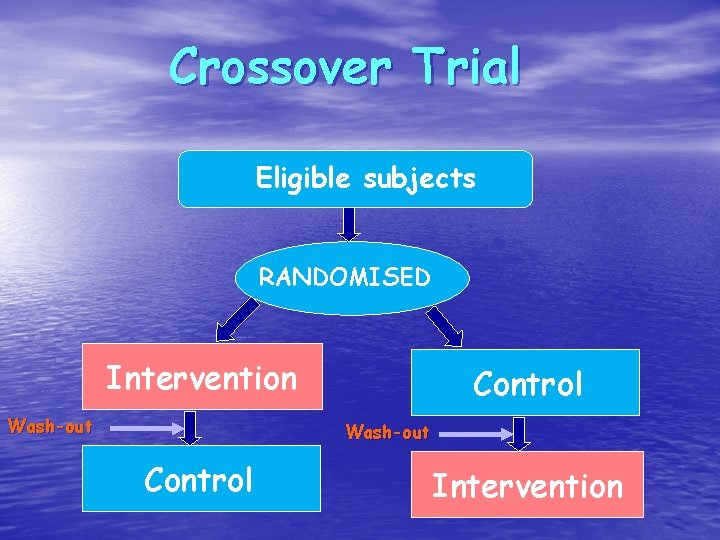
Crossover designs • In this design each patient receives ALL treatments • Comparison of treatments is withinpatient comparison • Removes all fixed within-patient factors e. g. gender • Essentially a matched design

Randomisation • Order of receipt is randomised • With 2 -period, 2 -treatments – AB or BA • With 3 -preriod, 3 -treatments – • ABC, ACB, BAC, BCA, CAB, CBA • Note above are balanced in the sense that every patient gets every treatment • Requires a wash-out period between treatments – to prevent CARRY-OVER

Crossover Trial Eligible subjects RANDOMISED Intervention Wash-out Control Intervention

Efficiency of Crossover design • To estimate efficiency we can compare the variances • For a similar parallel trial design: • Total number M = 2 N / (1 – rho) • Where M is the total size of the parallel trial and N is the number of subjects in the crossover design and rho is the correlation between measurements in Period I and II between a random subject • So a similar parallel trial design requires AT LEAST TWICE as many subjects

Strengths and Weaknesses of crossover design • Within patient characteristics remain same since matched analysis • Smaller sample size needed compared with parallel design - Very efficient design • Not suitable for intervention that ‘cures’ condition • Used for treatments of symptoms / control in chronic conditions; pain, asthma, COPD, diabetes, MS, hypertension, etc. • Fails if carry-over effect from previous period Senn S. (1993) Crossover trials in clinical research. Chichester, John Wiley

Simple Analysis Simple analysis makes use of the within-patient comparison: • Paired t-test for continuous outcomes • Mc. Nemar’s Chi-squared test for categorical data

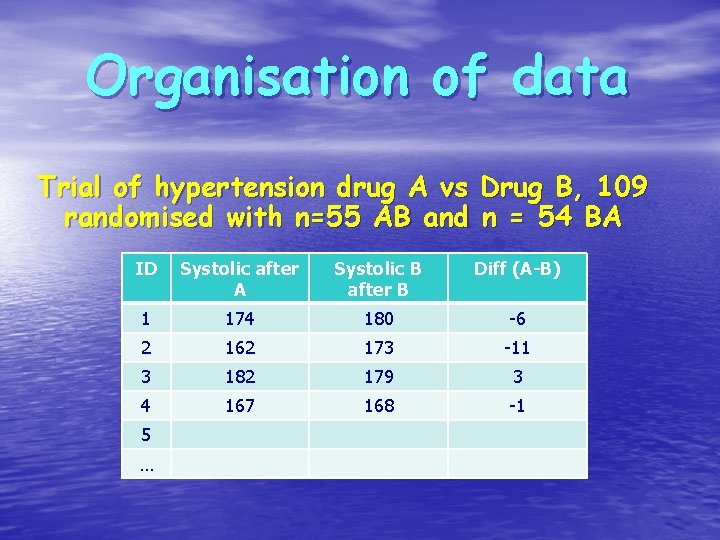
Organisation of data Trial of hypertension drug A vs Drug B, 109 randomised with n=55 AB and n = 54 BA ID Systolic after A Systolic B after B Diff (A-B) 1 174 180 -6 2 162 173 -11 3 182 179 3 4 167 168 -1 5 …

Paired t-test Trial of hypertension drug A vs Drug B, 109 randomised with n=55 AB and n = 54 BA t = Mean difference / Se (differences) = 3. 94 / 1. 67 = 2. 36 So with 108 df , p = 0. 02 • So a statistically significant effect with drug A generally lower BP • Analysis assumes no PERIOD effect and • No CARRY-OVER effect

Paired t-test In SPSS: Analyze Compare Means Paired-Samples t-test Then select two columns with the BP measurements for each drug

Examining the assumptions We can test for a PERIOD x TREATMENT interaction i. e. Does the effect of the drug vary depending on whether it is given in the first period compared to the second period? Common reason is CARRY-OVER Test for interaction is independent ttest for continuous outcome

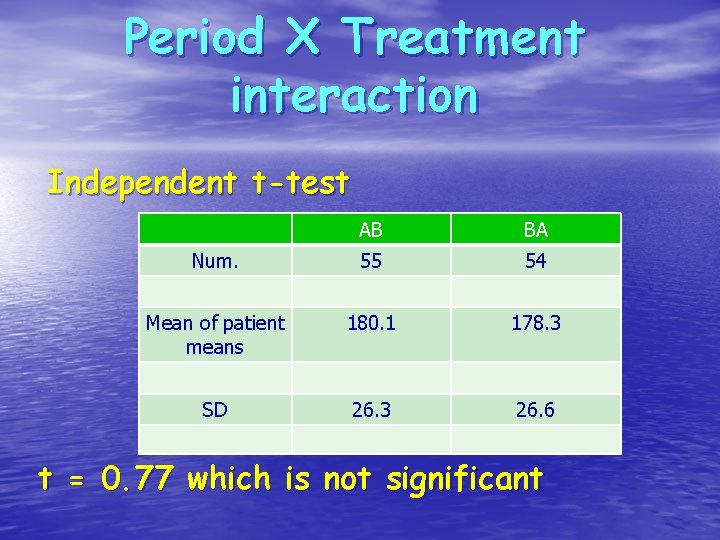
Period X Treatment interaction Independent t-test AB BA Num. 55 54 Mean of patient means 180. 1 178. 3 SD 26. 3 26. 6 t = 0. 77 which is not significant

Period X Treatment interaction Unfortunately the test is not very powerful and carry-over may not be detected with small sample size even if present (Solution: design study to be powerful enough!) If detected then the simple treatment analysis could be BIASED as the effect depends on which period the patients got which drug Then only use comparison in FIRST period for treatment effect (Grizzle two-step analysis).

Grizzle Two-stage analysis not recommended Senn (1994) says: • Two-step approach does not remove potential bias and carry-over test is usually underpowered • Test on period 1 is also underpowered • Best approach is to make sure there is NO carry-over with an efficient washout! • FDA recommend Washout ≥ 3 x halflife of drug

Senn’s advice Senn (1994) offers this advice: …my advice to the trialist is under no circumstances must the two-stage procedure be used. ”

Senn’s proposed analysis Make use of the two baseline measures in a two period design so we have four measurements ID Order Baseline BP (1=AB, A after A B after B 2=BA) Diff Baseline (A–B) Diff Outcome (A-B) 1 1 172 174 180 -8 -6 2 2 160 162 176 173 -4 -11 3 2 182 178 179 2 3 4 1 170 167 180 168 -10 -1 ….

Senn’s proposed analysis Use Generalised Linear Models (GLM) Fit simple SAS model as below: proc glm; class ORDER; model OUTCOME = ORDER BASELINE; Estimate ‘TREATMENT’ intercept 1; run; Intercept value is the TREATMENT effect and p-value Baseline can be removed to assess the effect of baseline in results

Senn’s proposed analysis Generalized Linear Models (GLM) include both continuous and categorical data and can be fitted in SPSS Analyze Generalized Linear Model etc… n. b. SPSS offers Generalized Estimating Equations (GEE) for binary outcomes

Other pitfalls • Patient drop-out in the first period can mean • • • there are fewer in the second period and potentially with different characteristics Analysis of only complete data or ‘Per Protocol’ is likely to be BIASED and breaks the Intention-To-Treat (ITT) principle Consider Multiple Imputation but assumes data is Missing-At-Random (MAR) Alternatively use Mixed Models (also assumes MAR)

Summary • • • Design is powerful and efficient Eliminates within-patient confounding Opportunity for head-to-head trials Problem of carry-over effect; test often underpowered Drop-outs break ITT principle and per protocol analysis could bias results

References Senn S. (2002) Crossover trials in clinical research. Chichester, John Wiley Mills JM, Chan A-W, Wu P, Vail A, Guyatt GH, Altman DG. Design, analysis and presentation of crossover trials. BMC Trials 2009; 10: 27 Schouten H and Kester A. A simple analysis of a simp[le crossover trial with a dichotomous outcome measure. Statist Med 2010; 29: 193 -198 Senn S. The AB/BA crossover: past, present and future? Statistical Methods in Medical Research 1994; 3: 303 -324.

Thank you for listening!