Cross Entropy The cross entropy for two distributions

Cross Entropy • The cross entropy for two distributions p and q over the same discrete probability space is defined as follows: H(p, q) = - x p(x) log(q(x)) not really a distance, because it is not symmetric

H(t, c) = - x t(x) log(q(c))

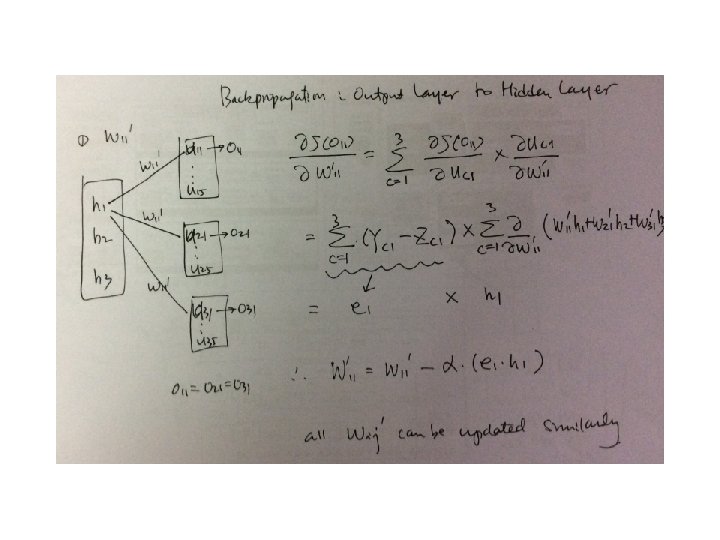
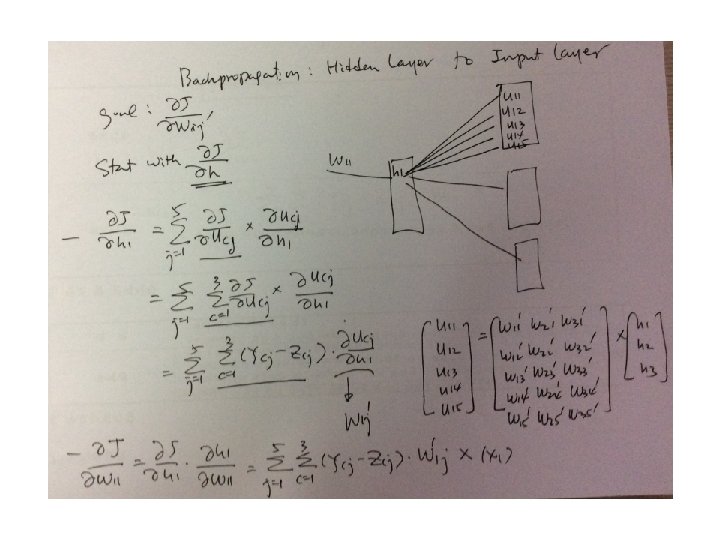
Gradient • Gradient with respect to the input of a softmax function when cross entropy loss is used.

Word 2 vec gradients shape(V) = shape(U) = |V| X d shape(x) = shape(y) = d X 1

Quiz 1. Derive the gradient of cross entropy 2. Derive the gradient of word 2 vec model with respect to a predictied word vector vc. 3. Derive the gradient for the output word vector uw.

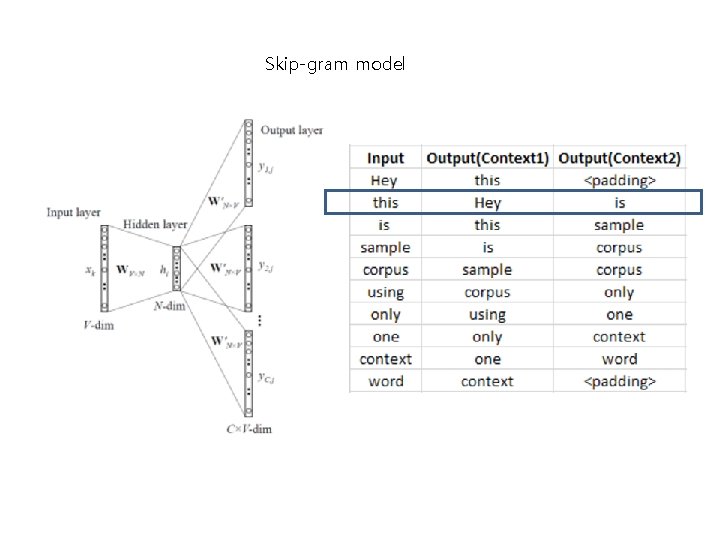
Skip-gram model

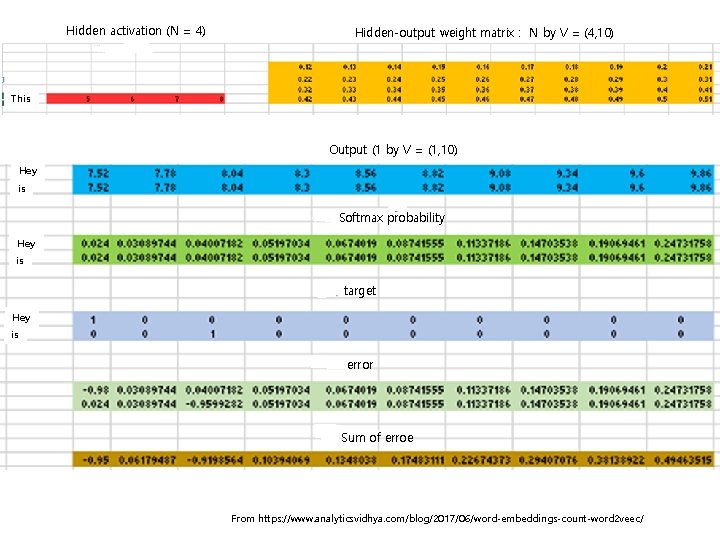
Hidden activation (N = 4) Hidden-output weight matrix : N by V = (4, 10) This Output (1 by V = (1, 10) Hey is Softmax probability Hey is target Hey is error Sum of erroe From https: //www. analyticsvidhya. com/blog/2017/06/word-embeddings-count-word 2 veec/

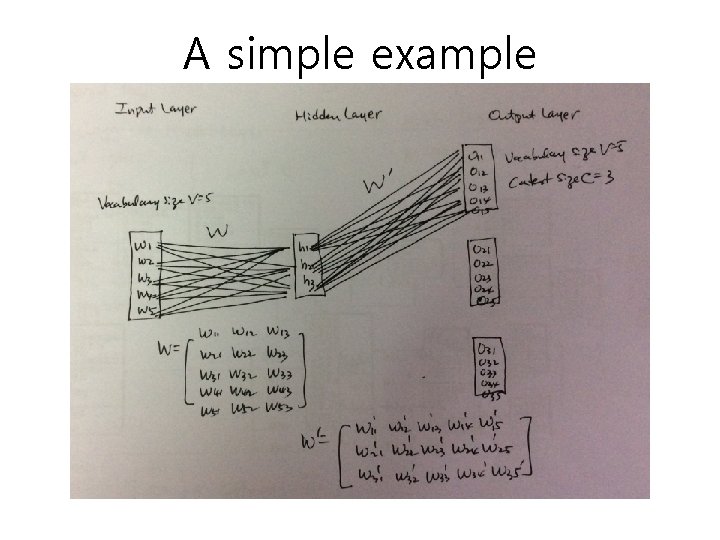
A simple example

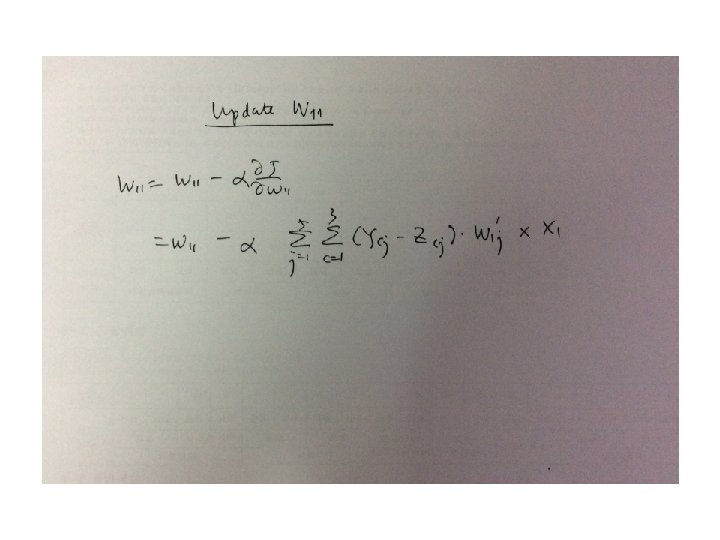
Negative sampling idea • Predicting the next word with cross-entropy requires normalization steps by means of softmax function, which is very costly • A key idea – a good model should be able to differentiate data from noise by means of logistic regression. • The idea is to convert a multinomial classification problem (as it is the problem of predicting the next word) to a binary classification problem. – That is, instead of using softmax to estimate a true probability distribution of the output word, a binary logistic regression (binary classification) is used instead. From https: //stats. stackexchange. com/questions/244616/how-sampling-works-in-word 2 vec-can-someone-please-make-me-understand-nce-and-ne

• Negative sampling: – Try to distinguish between words that do and words that do not occur in the context of the input word – Classification task – 1 positive example (from the ground truth) – k negative examples (from a random noise distribution

Negative sampling idea • Idea – For each training sample, the enhanced (optimized) classifier is fed a true pair (a center word another word that appears in its context) and a number of kk randomly corrupted pairs (consisting of the center word and a randomly chosen word from the vocabulary). – By learning to distinguish the true pairs from corrupted ones, the classifier will ultimately learn the word vectors. • This is important: instead of predicting the next word (the "standard" training technique), the optimized classifier simply predicts whether a pair of words is good or bad. From https: //stats. stackexchange. com/questions/244616/how-sampling-works-in-word 2 vec-can-someone-please-make-me-understand-nce-and-ne

From : http: //web. stanford. edu/class/cs 224 n/lectures/cs 224 n-2017 -lecture 3. pdf

Skip-Grams with Negative Sampling (SGNS) Marco saw a furry little wampimuk hiding in the tree. words wampimuk … contexts furry little hiding in … “word 2 vec Explained…” 27

Skip-Grams with Negative Sampling (SGNS) • “word 2 vec Explained…” 28 Goldberg & Levy, ar. Xiv

Skip-Grams with Negative Sampling (SGNS) • • “word 2 vec Explained…” 29 Goldberg & Levy, ar. Xiv

Skip-Grams with Negative Sampling (SGNS) • 30

Unigram model From : http: //www. phontron. com/slides/nlp-programming-en-01 -unigramlm. pdf Unigram model Bigram model

• Each word is given a weight equal to it’s frequency (word count) raised to the 3/4 power. The probability for a selecting a word is just it’s weight divided by the sum of weights for all words. • The decision to raise the frequency to the 3/4 power appears to be empirical; in their paper they say it outperformed other functions. • Why 3/4? – – – Here’s an example that might help gain some intuition: is: 0. 9^^(3/4) = 0. 92 Constitution: 0. 09^^(3/4) = 0. 16 bombastic: 0. 01^^(3/4) = 0. 032 "Bombastic" is now 3 x more likely to be sampled while "is" only went up marginally.

Hierarchical softmax • The idea is to decompose the softmax layer into a binary tree – with the words of the vocabulary at its leaves – the probability of a word given a context can be decomposed into probabilities of choosing the correct child at each node along the path from the root node to that leaf. – This reduces the number of necessary updates from a linear to a logarithmic term in the vocabulary size.

Soft. Max Word Input Output King [0. 2, 0. 9, 0. 1] [0. 5, 0. 4, 0. 5] Queen [0. 2, 0. 8, 0. 2] [0. 4, 0. 5] Apple [0. 9, 0. 5, 0. 8] [0. 3, 0. 9, 0. 1] [0. 9, 0. 4, 0. 9] Distributed Representations of Words and. Orange Phrases and their Compositionality. Mikolov at al. , 2013 [0. 1, 0. 7, 0. 2]

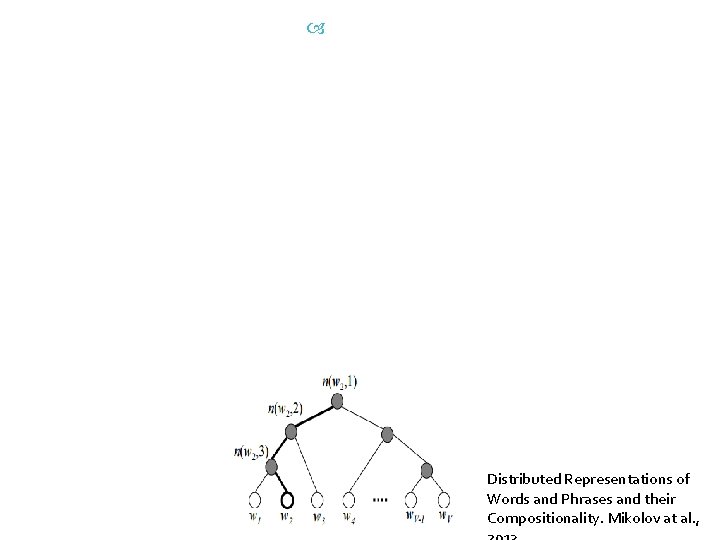
Distributed Representations of Words and Phrases and their Compositionality. Mikolov at al. ,

The T words are represented as leaves, and form a full binary tree along with T – 1 internal nodes. Hierarchic al Soft. Max Each word has a single vector representation vw and each internal node n is represented by a vector vn. The path from the root to a leaf is used to estimate the probability of the word represented by this leaf It can be shown that the word 2 vecof Parameter Learning Explained, probabilities all leaves sum up to. Xin

Hierarchic al Soft. Max Distributed Representations of Words and Phra their Compositionality. Mikolov at al. , 2013