Cronnelly Warmup Warmup Warmup Step 1 Order Numbers

Cronnelly

Warm-up

Warm-up
Warm-up

Step 1 – Order Numbers 1. Order the set of numbers from least to greatest

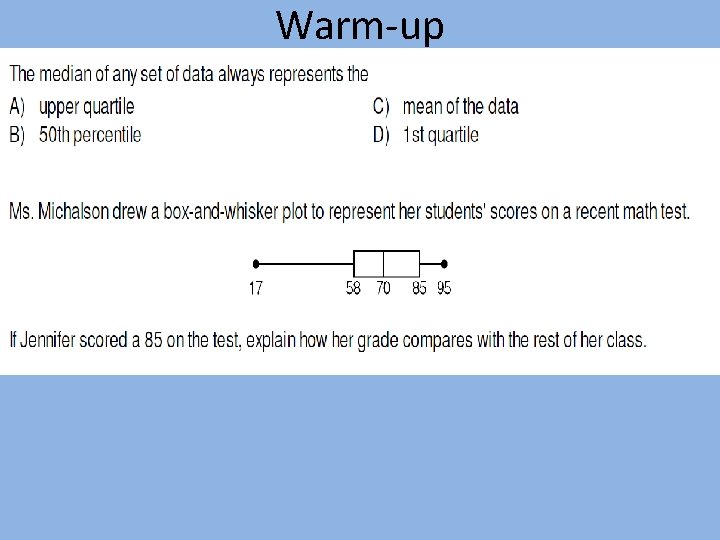
Step 2 – Find the Median 2. Find the median. The median is the middle number. If the data has two middle numbers, find the mean of the two numbers. What is the median?
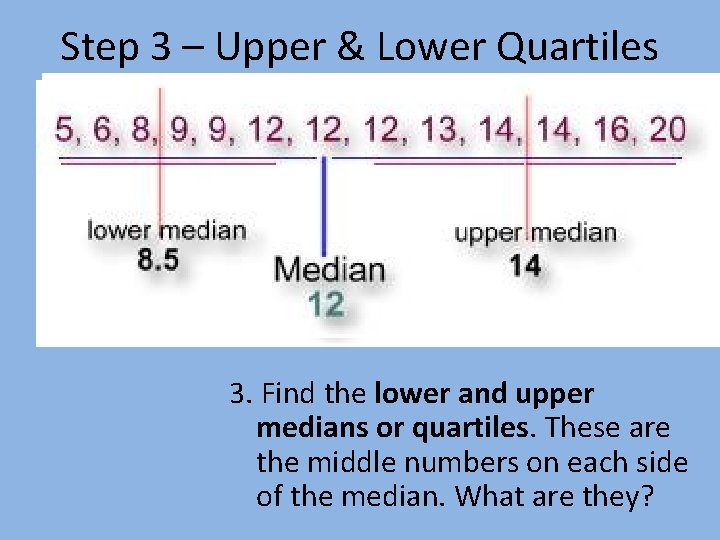
Step 3 – Upper & Lower Quartiles 3. Find the lower and upper medians or quartiles. These are the middle numbers on each side of the median. What are they?
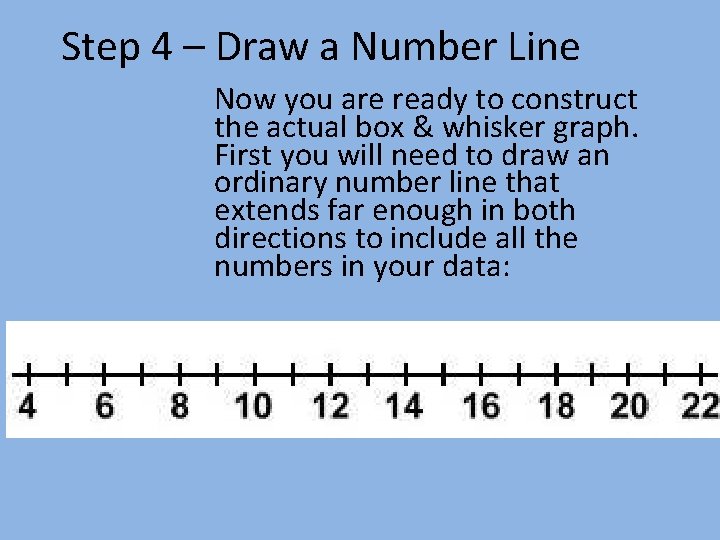
Step 4 – Draw a Number Line Now you are ready to construct the actual box & whisker graph. First you will need to draw an ordinary number line that extends far enough in both directions to include all the numbers in your data:
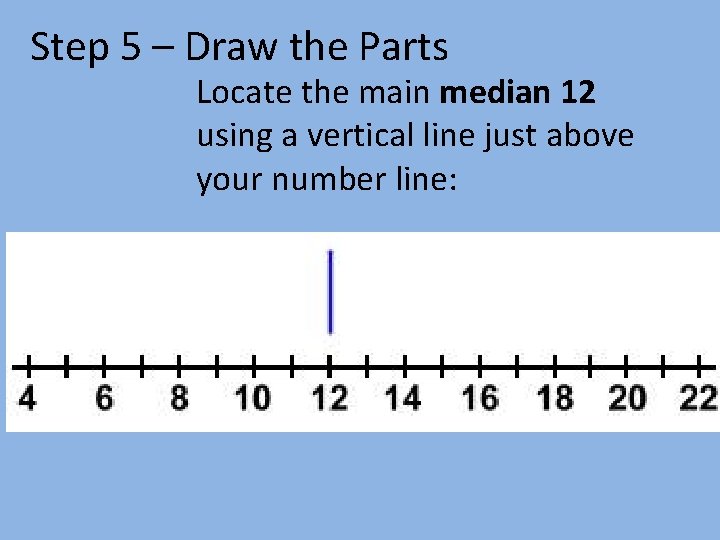
Step 5 – Draw the Parts Locate the main median 12 using a vertical line just above your number line:
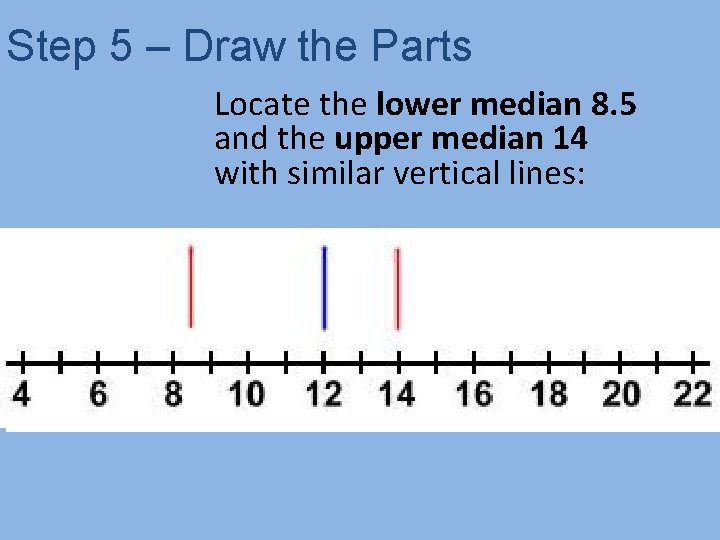
Step 5 – Draw the Parts Locate the lower median 8. 5 and the upper median 14 with similar vertical lines:
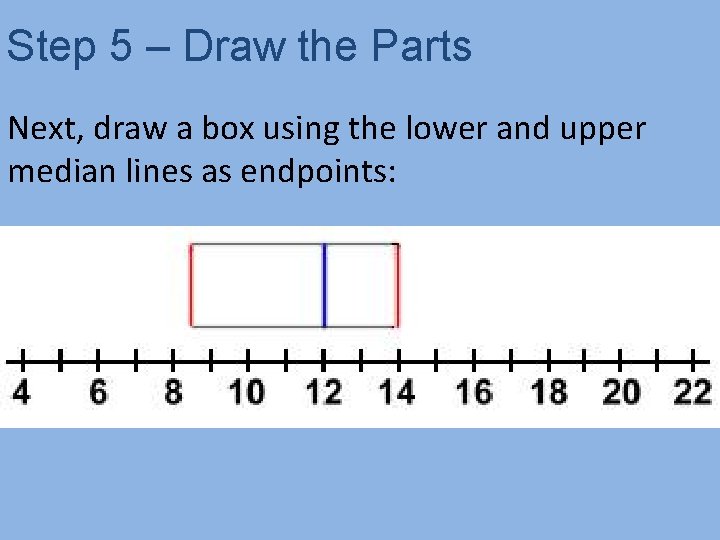
Step 5 – Draw the Parts Next, draw a box using the lower and upper median lines as endpoints:
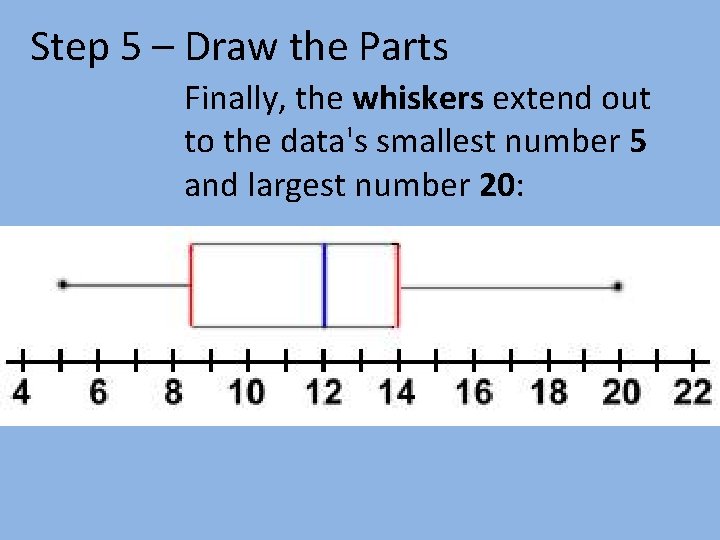
Step 5 – Draw the Parts Finally, the whiskers extend out to the data's smallest number 5 and largest number 20:
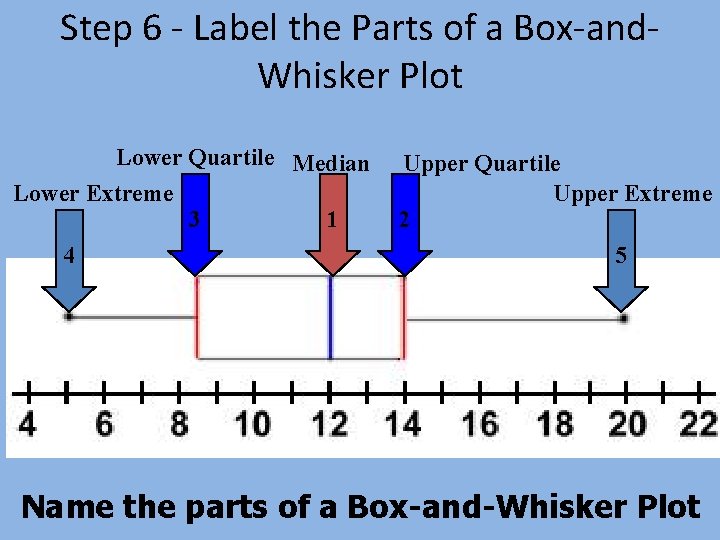
Step 6 - Label the Parts of a Box-and. Whisker Plot Lower Quartile Median Lower Extreme 3 1 4 Upper Quartile Upper Extreme 2 5 Name the parts of a Box-and-Whisker Plot

Even Numbered Data Sets If the data set has an even number of pieces of data, we find the mean of the two middle numbers to find the median of the set 2, 4, 5, 6, 7, 8, 9, 11, 19, 20 7 + 8 = 15 15 divided by 2 = 7. 5 The median is 7. 5

Even Numbered Data Sets • The median splits the data set in half. [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] • From here we can then find the upper and lower quartiles as well as the upper and lower extremes.

Lower Quartile • The lower quartile is the median of the bottom half of the data (to the left of the median). [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] Lower Quartile for this data = 5

Upper Quartile • The upper quartile is the median of the top half of the data (to the right of the median). [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] The upper quartile for this data set = 11

Interquartile Range To find the interquartile range, subtract the lower quartile from the upper quartile. Upper Quartile – Lower Quartile = _____ [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] 11 – 5 =6 The interquartile range for this data = 6

Lower Extreme • The lower extreme is the lowest number in the data set. [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] The lower extreme for this data set = 2

Upper Extreme • The upper extreme is the highest number in the data set. [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] The upper extreme for this data set = 20

Range • The range of the data can be found by subtracting the lower extreme from the upper extreme. [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] 20 – 2 = 18 The range for this data set = 18
![Even Numbered Data Sets [ 2, 4, 5, 6, 7] 7. 5 [8, 9, Even Numbered Data Sets [ 2, 4, 5, 6, 7] 7. 5 [8, 9,](http://slidetodoc.com/presentation_image_h/1b1b4894ebca23486ce8975abc201265/image-23.jpg)
Even Numbered Data Sets [ 2, 4, 5, 6, 7] 7. 5 [8, 9, 11, 19, 20] • • • Median = 7. 5 Lower Quartile = 5 Upper Quartile = 11 Upper Extreme = 20 Lower Extreme = 2

Sample Problem • Use the following data set to create a 5 number summary • 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

Sample Problem • What is the median? 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 The median is the mean of 6 and 7 The median is 6. 5

Sample Problem • Remember, the median splits the data set in half [1, 2, 3, 4, 5, 6] 6. 5 [7, 8, 9, 10, 11, 12]
![Sample Problem • What are the quartiles? [1, 2, 3, 4, 5, 6] 6. Sample Problem • What are the quartiles? [1, 2, 3, 4, 5, 6] 6.](http://slidetodoc.com/presentation_image_h/1b1b4894ebca23486ce8975abc201265/image-27.jpg)
Sample Problem • What are the quartiles? [1, 2, 3, 4, 5, 6] 6. 5 [7, 8, 9, 10, 11, 12] • Lower Quartile = 3. 5 • Upper Quartile = 9. 5

Sample Problem • What is the upper extreme? • What is the lower extreme? [1, 2, 3, 4, 5, 6] 6. 5 [7, 8, 9, 10, 11, 12] • Upper Extreme = 12 • Lower Extreme = 1

Sample Problem • • • What is the 5 number summary? Median = 6. 5 Lower Quartile = 3. 5 Upper Quartile = 9. 5 Upper Extreme = 12 Lower Extreme = 1

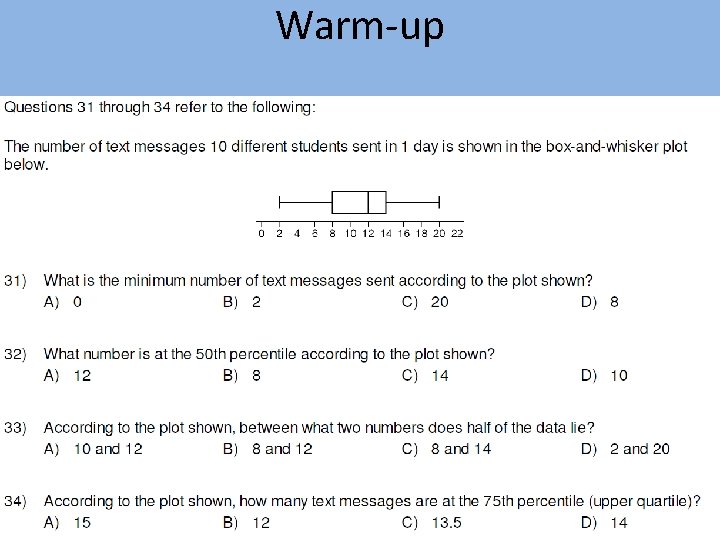
worksheet Finding the median, quartiles and inter-quartile range. Example 1: Find the median and quartiles for the data below. 12, 6, 4, 9, 8, 5, 9, 8, 10 Example 2: Find the median and quartiles for the data below. 6, 3, 9, 8, 4, 10, 8, 4, 15, 8, 10

worksheet Finding the median, quartiles and inter-quartile range. Example 3: Find the median and quartiles for the data below. 177, 185, 132, 147, 164, 158, 181, 173, 169, 152, 139, 141, 189 Example 4: Find the median and quartiles for the data below. 49, 21, 32, 51, 26, 37, 53, 29, 39, 57, 61, 63
worksheet Box Plots 1 2 4 3 4 5 5 6 6 7 7 8 8 9 9 10 11 12 12 13 14 15 3 130 140 4 0 150 10 160 20 30 170 40 180 50 cm 60 190
- Slides: 32