Critical slowing down as an indicator of transitions

Critical slowing down as an indicator of transitions in two-species models Ryan Chisholm Smithsonian Tropical Research Institute Workshop on Critical Transitions in Complex Systems 21 March 2012 Imperial College London

Acknowledgements • Elise Filotas, Centre for Forest Research at the University of Quebec in Montreal • Simon Levin, Princeton University, Department of Ecology and Evolutionary Biology • Helene Muller-Landau, Smithsonian Tropical Research Institute • Santa Fe Institute, Complex Systems Summer School 2007: NSF Grant No. 0200500

Question When is critical slowing down likely to be a useful leading indicator of a critical transition in ecological models?

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

Smithsonian Tropical Research Institute • “…dedicated to understanding biological diversity” • What determines patterns of diversity? • What factors regulate ecosystem function? • How will tropical forests respond to climate change and other anthropogenic disturbances?

Smithsonian Tropical Research Institute Panama

Smithsonian Tropical Research Institute 50 ha plot

Smithsonian Tropical Research Institute 1500 ha 2551 mm yr-1 rainfall 381 bird species 102 mammal species (nearly half are bats) • ~100 species of amphibians and reptiles • 1316 plant species • • Green iguana (Iguana iguana) Pentagonia macrophylla Keel-billed Toucan (Ramphastos sulfuratus) Jaguar (Panthera onca) Photo: Christian Ziegler

Smithsonian Tropical Research Institute Photo: Marcos Guerra, STRI Photo: Leonor Alvarez sciencedaily. com

Center for Tropical Forest Science

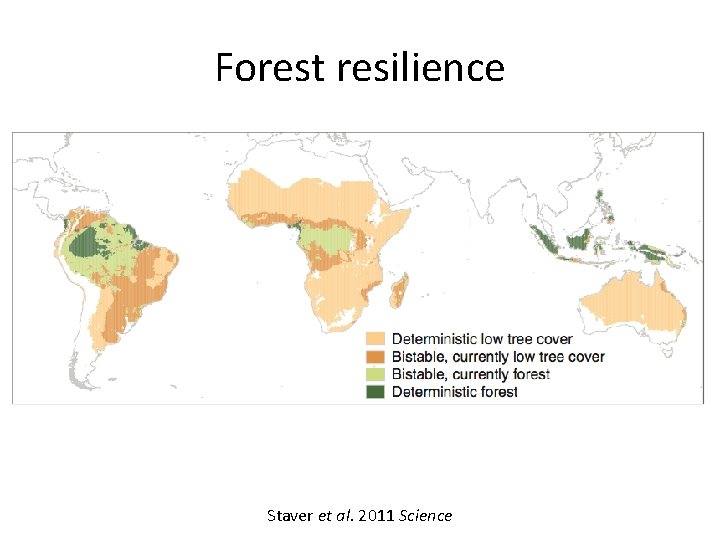
Forest resilience Staver et al. 2011 Science

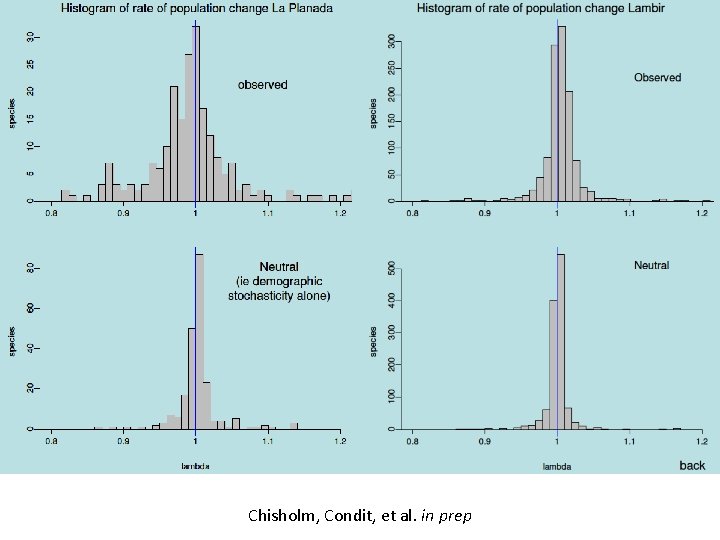
Chisholm, Condit, et al. in prep

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

Transitions in complex systems • • • Eutrophication of shallow lakes Sahara desertification Climate change Shifts in public opinion Forest-savannah transitions Scheffer et al. 2009 Nature, Scheffer 2009 Critical Transitions in Nature and Society

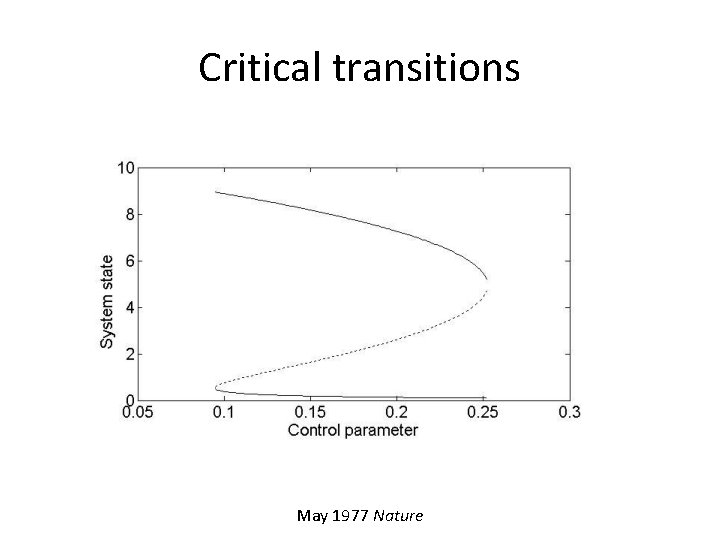
Critical transitions May 1977 Nature

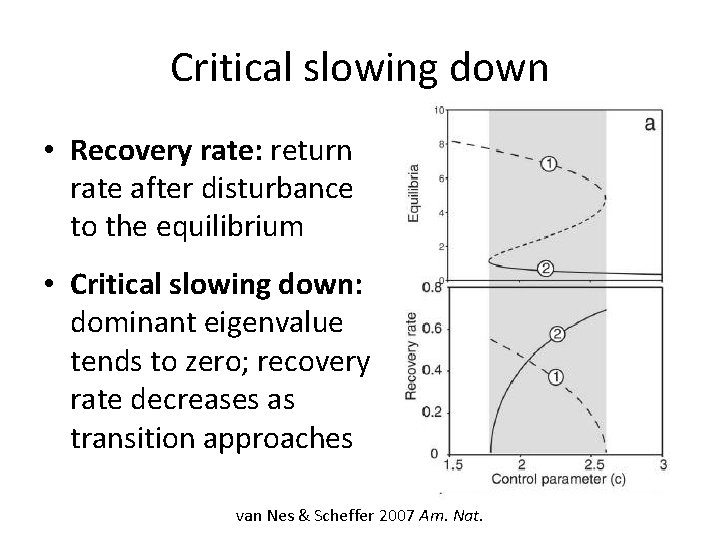
Detecting impending transitions • Decreasing return rate • Rising variance • Rising autocorrelation => All arise from critical slowing down Carpenter & Brock 2006 Ecol. Lett. , van Nes & Scheffer 2007 Am. Nat. , Scheffer et al. 2009 Nature

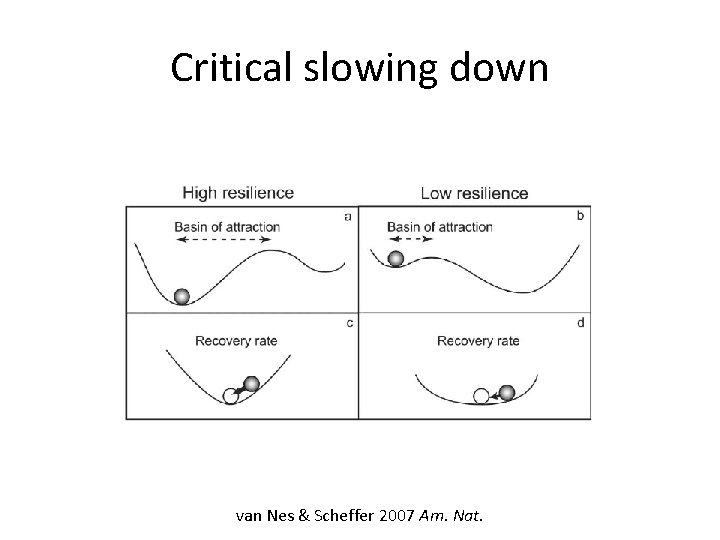
Critical slowing down • Recovery rate: return rate after disturbance to the equilibrium • Critical slowing down: dominant eigenvalue tends to zero; recovery rate decreases as transition approaches van Nes & Scheffer 2007 Am. Nat.

Critical slowing down van Nes & Scheffer 2007 Am. Nat.

Critical slowing down van Nes & Scheffer 2007 Am. Nat.

Question When is critical slowing down likely to be a useful leading indicator of a critical transition in ecological models? What is the length/duration of the warning period?

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

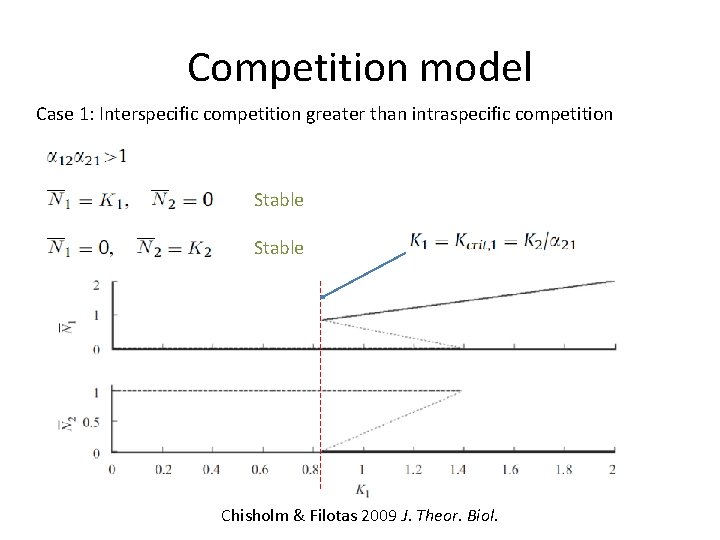
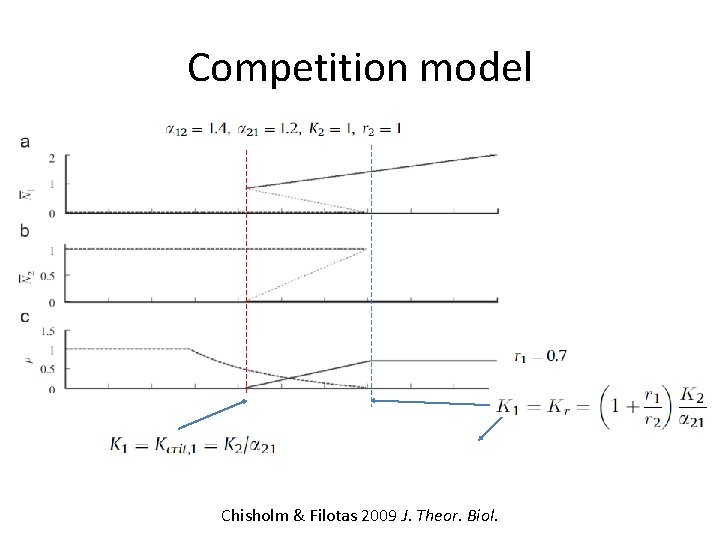
Competition model Ni = abundance of species i Ki = carrying capacity of species i ri = intrinsic rate of increase of species i αij = competitive impact of species j on species i Equilibria: Lotka 1925, 1956 Elements of Physical Biology; Chisholm & Filotas 2009 J. Theor. Biol.

Competition model Case 1: Interspecific competition greater than intraspecific competition Stable Unstable Chisholm & Filotas 2009 J. Theor. Biol.

Question When is critical slowing down likely to be a useful leading indicator of a critical transition in ecological models? What is the length/duration of the warning period?

Competition model Ni = abundance of species i Ki = abundance of species i ri = intrinsic rate of increase of species i αij = competitive impact of species j on species i Recovery rate: When species 1 dominates, recovery rate begins to decline at: Chisholm & Filotas 2009 J. Theor. Biol.

Competition model Chisholm & Filotas 2009 J. Theor. Biol.

Competition model Ni = abundance of species i Ki = abundance of species i ri = intrinsic rate of increase of species i αij = competitive impact of species j on species i Recovery rate begins to decline at: More warning of transition if the dynamics of the rare species are slow relative to those of the dominant species Chisholm & Filotas 2009 J. Theor. Biol.

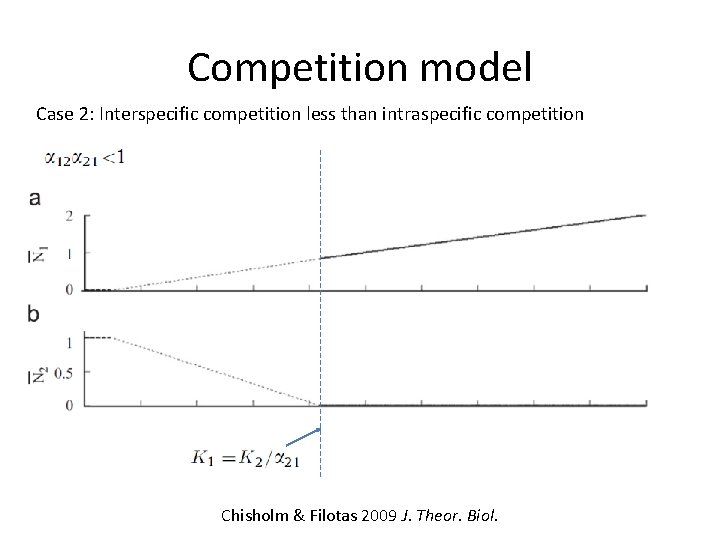
Competition model Case 2: Interspecific competition less than intraspecific competition Stable Unstable Stable Chisholm & Filotas 2009 J. Theor. Biol.

Competition model Case 2: Interspecific competition less than intraspecific competition More warning of transition if the dynamics of the rare species are slow relative to those of the dominant species Chisholm & Filotas 2009 J. Theor. Biol.

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

Predator-prey model V = prey abundance P = predator abundance Rosenzweig 1971 Science

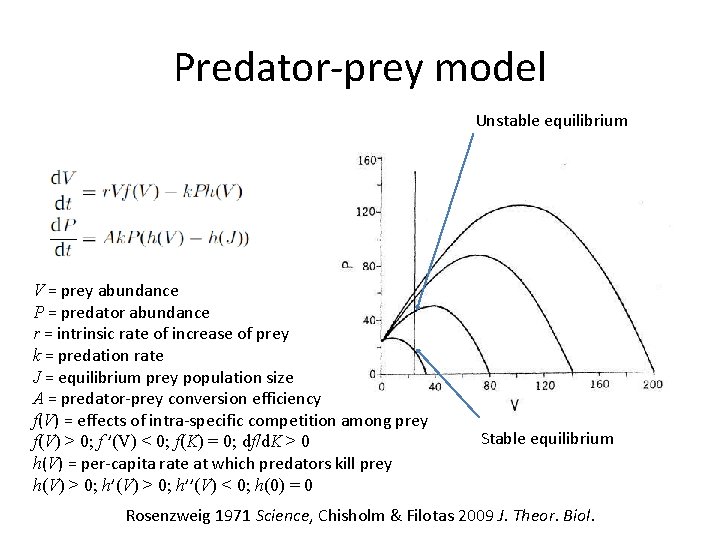
Predator-prey model h(V) V = prey abundance P = predator abundance r = intrinsic rate of increase of prey k = predation rate J = equilibrium prey population size A = predator-prey conversion efficiency K = carrying capacity of prey f(V) = effects of intra-specific competition among prey f(V) > 0; f ’(V) < 0; f(K) = 0; df/d. K > 0 h(V) = per-capita rate at which predators kill prey h(V) > 0; h’’(V) < 0; h(0) = 0 f(V) V Rosenzweig 1971 Science, Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Equilibria: Unstable Stable for K ≤ J V = prey abundance P = predator abundance r = intrinsic rate of increase of prey k = predation rate J = equilibrium prey population size A = predator-prey conversion efficiency K = carrying capacity of prey f(V) = effects of intra-specific competition among prey f(V) > 0; f ’(V) < 0; f(K) = 0; df/d. K > 0 h(V) = per-capita rate at which predators kill prey h(V) > 0; h’’(V) < 0; h(0) = 0 Exists for K ≥ J Stable for J ≤ Kcrit Rosenzweig 1971 Science, Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Predator isocline V = prey abundance P = predator abundance r = intrinsic rate of increase of prey k = predation rate J = equilibrium prey population size A = predator-prey conversion efficiency f(V) = effects of intra-specific competition among prey f(V) > 0; f ’(V) < 0; f(K) = 0; df/d. K > 0 h(V) = per-capita rate at which predators kill prey h(V) > 0; h’’(V) < 0; h(0) = 0 Prey isoclines Rosenzweig 1971 Science, Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Unstable equilibrium V = prey abundance P = predator abundance r = intrinsic rate of increase of prey k = predation rate J = equilibrium prey population size A = predator-prey conversion efficiency f(V) = effects of intra-specific competition among prey f(V) > 0; f ’(V) < 0; f(K) = 0; df/d. K > 0 h(V) = per-capita rate at which predators kill prey h(V) > 0; h’’(V) < 0; h(0) = 0 Stable equilibrium Rosenzweig 1971 Science, Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Scheffer 1998 The Ecology of Shallow Lakes

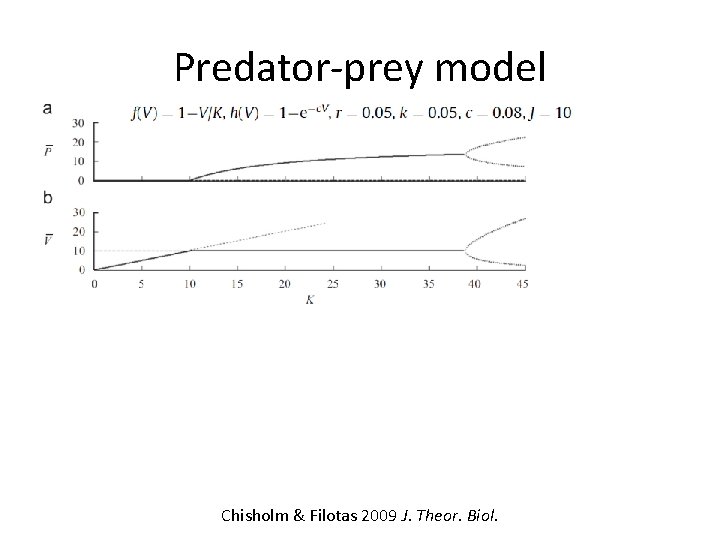
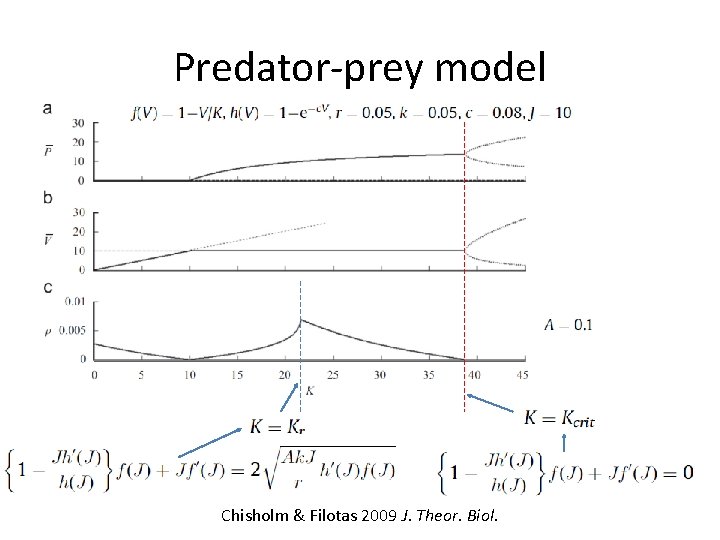
Predator-prey model Hopf bifurcation occurs when K = Kcrit : Critical slowing down begins when K = Kr :

Predator-prey model Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Chisholm & Filotas 2009 J. Theor. Biol.

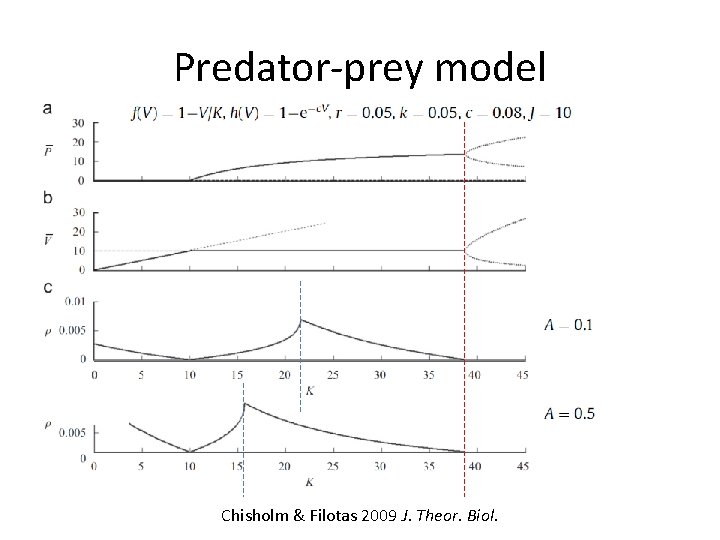
Predator-prey model Kr and Kcrit converge as: More warning of transition when: • Predator-prey conversion efficiency (A) is high • Predation rate (k) is high • Prey growth rate (r) is low Þ Prey controlled by predators rather than intrinsic density dependence Þ Increases tendency for oscillations Þ Larger K makes oscillations larger and hence rates of return slower Chisholm & Filotas 2009 J. Theor. Biol.

Predator-prey model Chisholm & Filotas 2009 J. Theor. Biol.

Multi-species models van Nes & Scheffer 2007 Am. Nat.

Multi-species models Expect that multi-species models will exhibit longer warning periods of transitions induced by changes in resource abundance when: • Dynamics of rare species are slow relative to those of the dominant species • Prey species are controlled by predation rather than intrinsic density dependence Chisholm & Filotas 2009 J. Theor. Biol.

Outline • • • Smithsonian Tropical Research Institute Background: critical slowing down Competition model Predator-prey model Grasslands model Future work

Practical utility of critical slowing down Chisholm & Filotas 2009 J. Theor. Biol. “…even if an increase in variance or AR 1 is detected, it provides no indication of how close to a regime shift the ecosystem is…” Biggs et al. 2008 PNAS

Western Basalt Plains Grasslands

Western Basalt Plains Grasslands

Western Basalt Plains Grasslands Williams et al. 2005 J. Ecol. ; Williams et al. 2006 Ecology

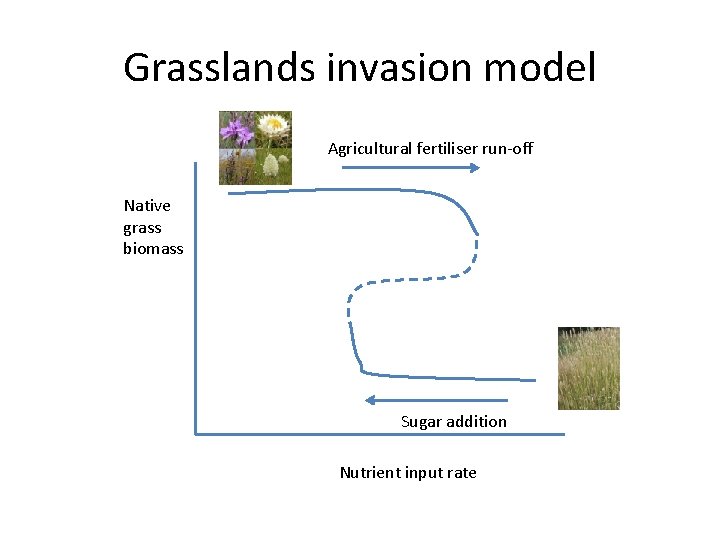
Grasslands invasion model Agricultural fertiliser run-off Native grass biomass Sugar addition Nutrient input rate

Grasslands invasion model A = plant-available N pool Bi = biomass of species i ωi = N-use efficiency of species i νi = N-use efficiency of species i μi = N-use efficiency of species i αij = light competition coefficients I = abiotic N-input flux K = soil leaching rate of plant-available N δ = proportion of N in litterfall lost from the system Parameterized so that species 2 (invader) has a higher uptake rate and higher turnover rate. Chisholm & Levin in prep. ; Menge et al. 2008 PNAS

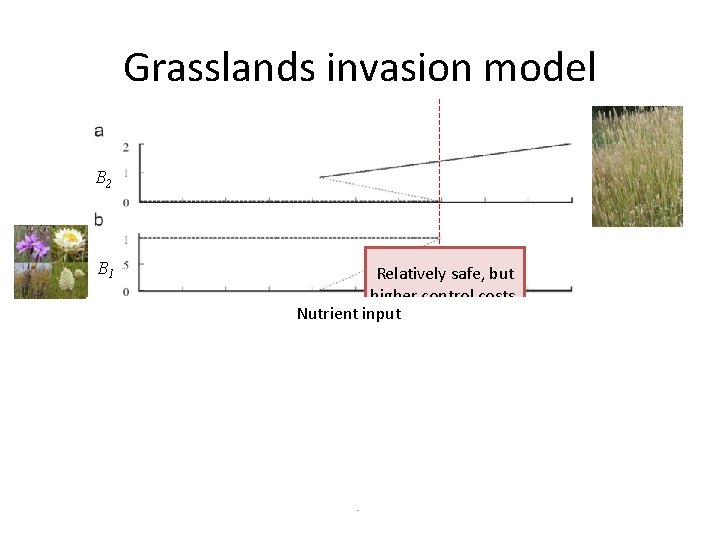
Grasslands invasion model B 2 B 1 Relatively safe, but higher control costs. Nutrient input Riskier, but lower control costs.

Conclusions & Future work Critical slowing down provides an earlier indicator of transitions in two-species models where: • Dynamics of rare species are slow relative to those of the dominant species • Prey species are controlled by predation rather than intrinsic density dependence But utility of early/late indicators depends on socio-economic considerations