Critical graphs and facets of the stable set

Critical graphs and facets of the stable set polytope László Lipták László Lovász The Fields Institute Microsoft Research University of Toronto One Microsoft Way, Toronto, Ontario, Canada lliptak@fields. utoronto. ca Redmond, WA 98052 lovasz@microsoft. com
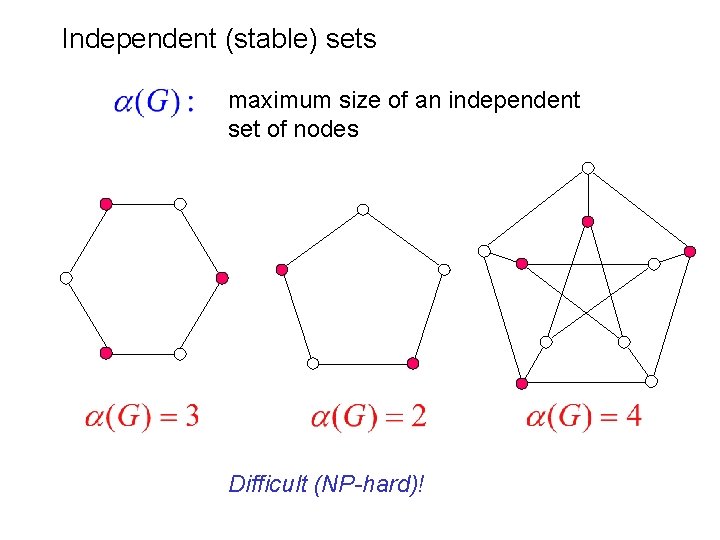
Independent (stable) sets maximum size of an independent set of nodes Difficult (NP-hard)!
![α-critical graphs [no isolated nodes; connected] α-critical graphs [no isolated nodes; connected]](http://slidetodoc.com/presentation_image_h/8bdcd306060c52d8ecdfb1cbc31ec2a9/image-3.jpg)
α-critical graphs [no isolated nodes; connected]
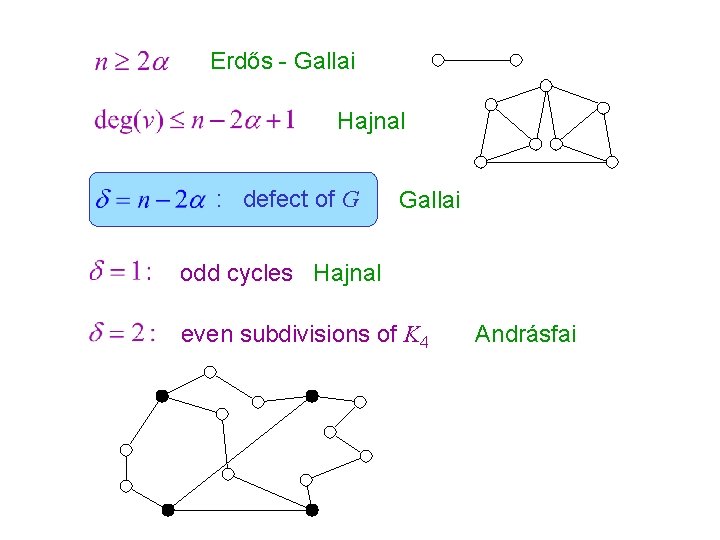
Erdős - Gallai Hajnal : defect of G Gallai odd cycles Hajnal even subdivisions of K 4 Andrásfai
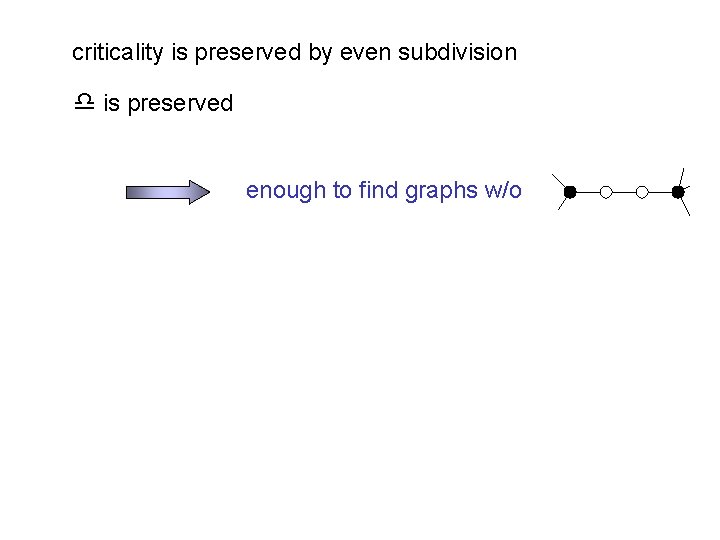
criticality is preserved by even subdivision d is preserved enough to find graphs w/o
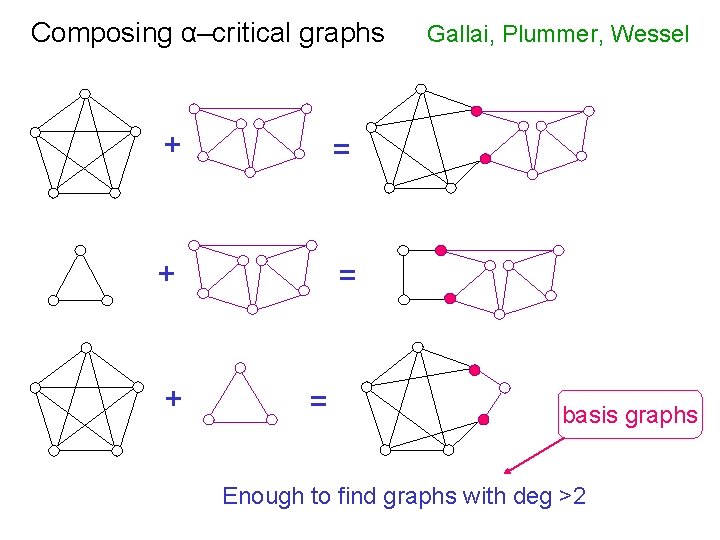
Composing α–critical graphs + = + = Gallai, Plummer, Wessel basis graphs Enough to find graphs with deg >2
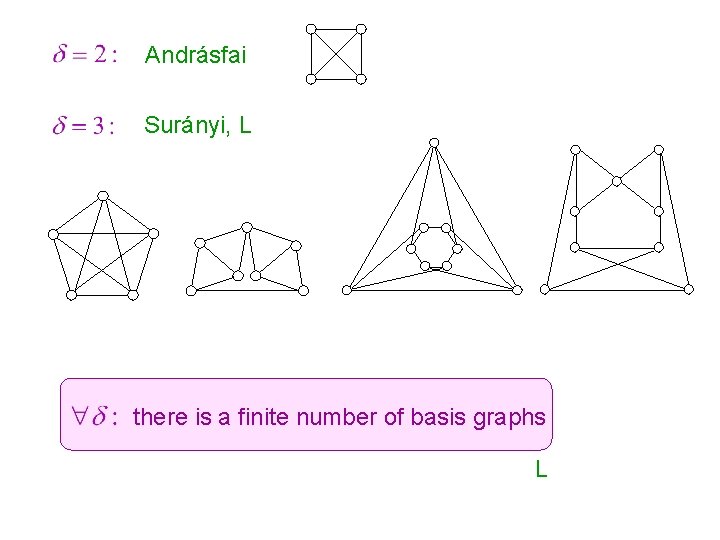
Andrásfai Surányi, L there is a finite number of basis graphs L
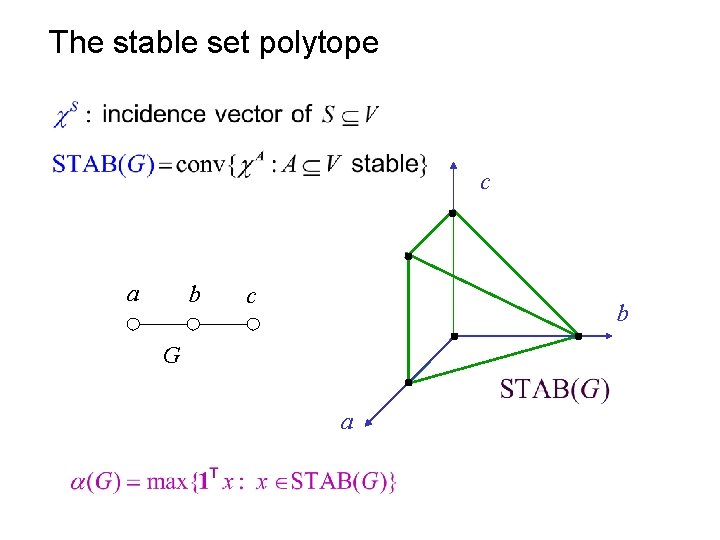
The stable set polytope c a b c b G a
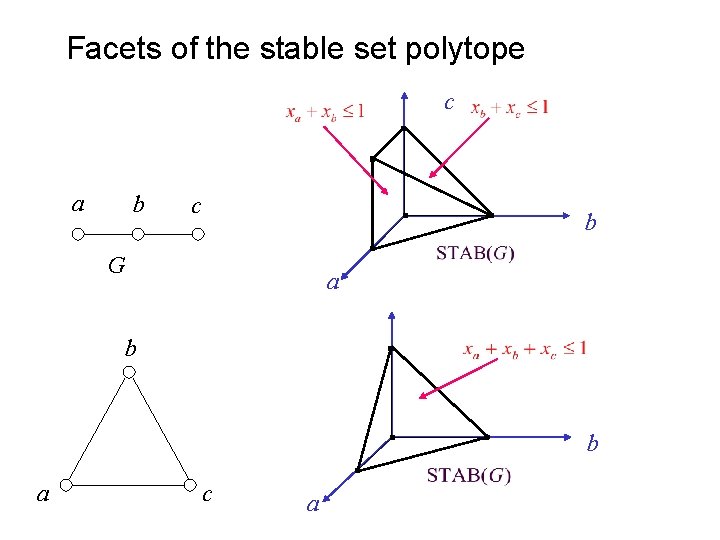
Facets of the stable set polytope c a b c b G a b b a c a
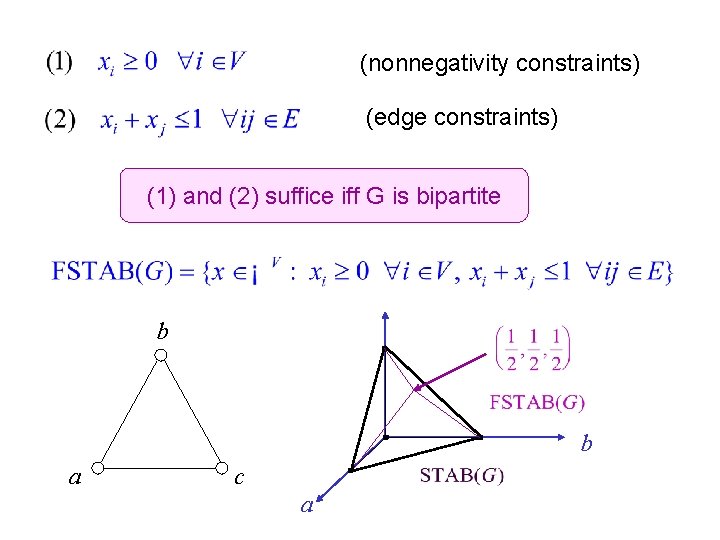
(nonnegativity constraints) (edge constraints) (1) and (2) suffice iff G is bipartite b b a c a

(clique constraints) (1) and (3) suffice iff G is perfect Fulkerson-Chvátal (odd hole constraints) (rank constraints) G -critical rank constraint for U=V is a facet Chvátal View facets as generalizations of -critical graphs

nontrivial facet of STAB(G): vertex of this facet: stable set integrality gap of this facet: defect of facet non-trivial L-Schrijver
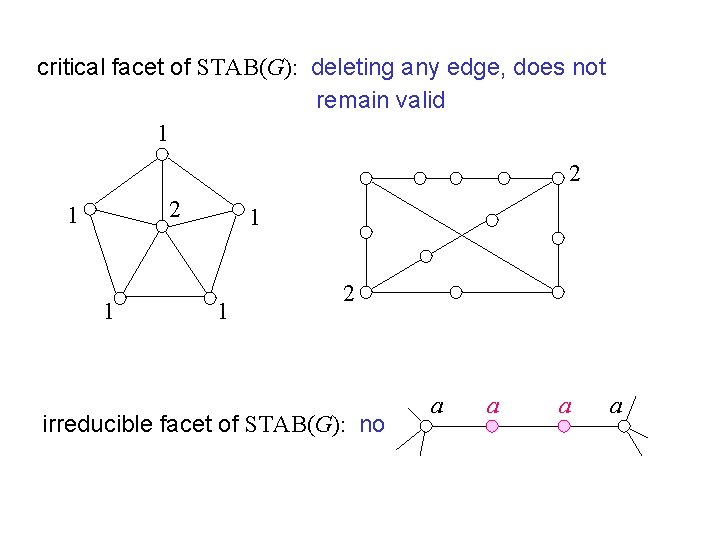
critical facet of STAB(G): deleting any edge, does not remain valid 1 2 2 1 1 2 irreducible facet of STAB(G): no a a
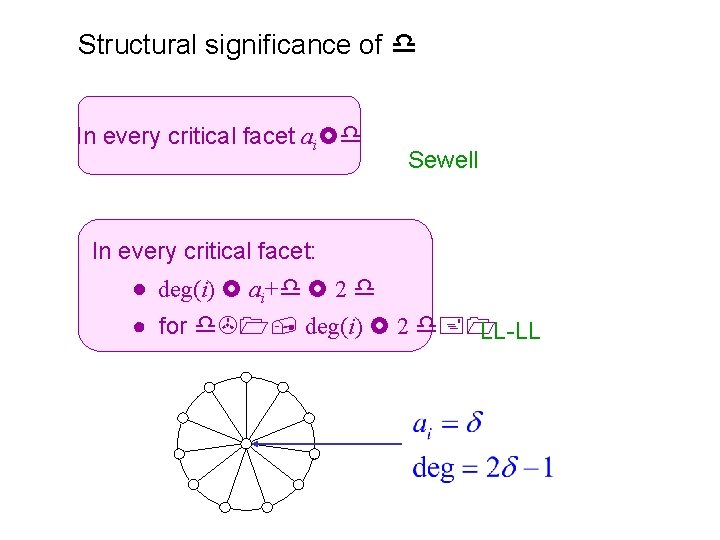
Structural significance of d In every critical facet ai d Sewell In every critical facet: ● deg(i) ai+d 2 d ● for d>1, deg(i) 2 d+1 LL-LL
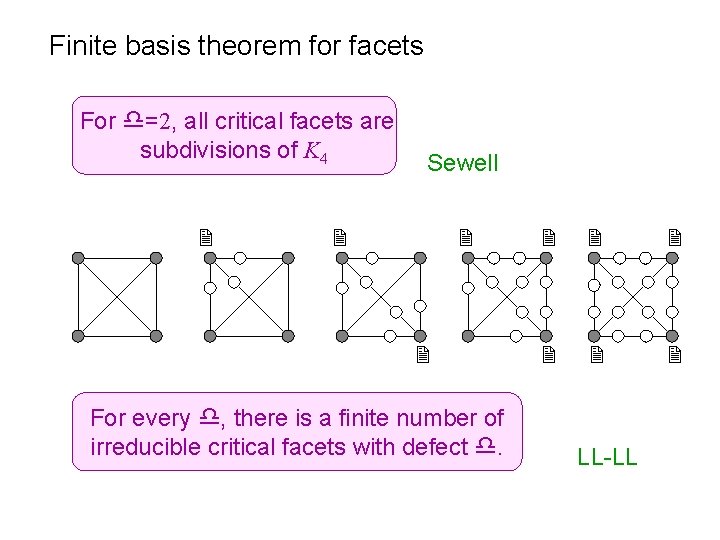
Finite basis theorem for facets For d=2, all critical facets are subdivisions of K 4 2 Sewell 2 2 2 For every d, there is a finite number of irreducible critical facets with defect d. 2 2 2 LL-LL

Deriving facets trivial constraints (edge constraints)
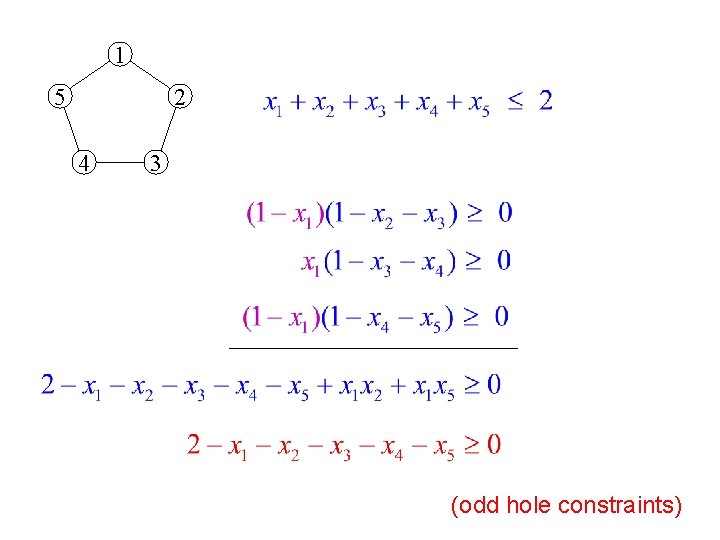
1 5 2 4 3 (odd hole constraints)
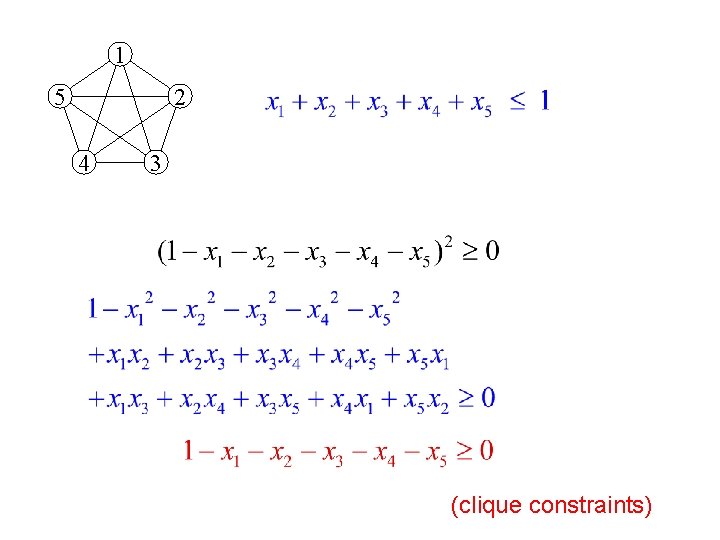
1 5 2 4 3 (clique constraints)
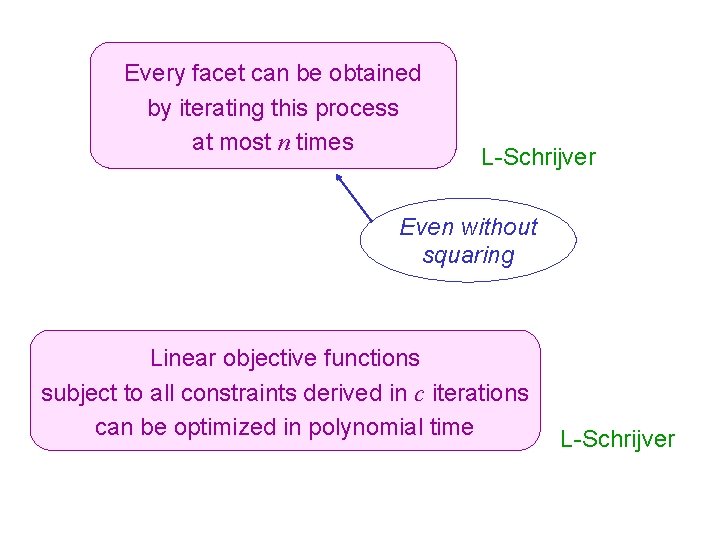
Every facet can be obtained by iterating this process at most n times L-Schrijver Even without squaring Linear objective functions subject to all constraints derived in c iterations can be optimized in polynomial time L-Schrijver

Which facets can be derived in c iterations? rank of facet: smallest c r: rank of d : defect of L-Schrijver

odd hole contraints ? The average degree of a critical facet with rank r is <2 r. Lipták
- Slides: 21