Critical dynamics on a large human Open Connectome

Critical dynamics on a large human Open Connectome network Géza Ódor MTA-MFA Complex Systems, Budapest Michael Gastner Yale-Nus college, Singapore Variability and heterogeneities of neural networks are important and make brain more efficient (see : Neuron 92 (2016) 53054 ) Theoretical research and experiments suggest that the brain operates at or near a critical state between sustained activity and an inactive phase, exhibiting optimal computational properties (see: PRL 110, 178101 (2013)) Criticality is affected by heterogeneities in spreading models in case of finite topological dimensions (see: PRL. 105 (2010) 128701. ) What is the topological dimension of available connectome graphs ? Are they small world-like ? Are they scale-free ? Critical dynamics ?

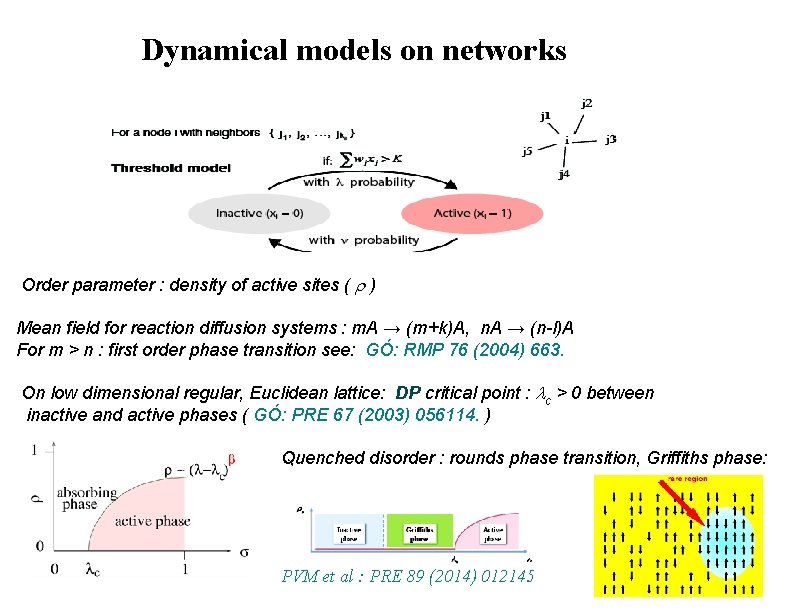
Dynamical models on networks Order parameter : density of active sites ( ) Mean field for reaction diffusion systems : m. A → (m+k)A, n. A → (n-l)A For m > n : first order phase transition see: GÓ: RMP 76 (2004) 663. On low dimensional regular, Euclidean lattice: DP critical point : c > 0 between inactive and active phases ( GÓ: PRE 67 (2003) 056114. ) Quenched disorder : rounds phase transition, Griffiths phase: PVM et al : PRE 89 (2014) 012145

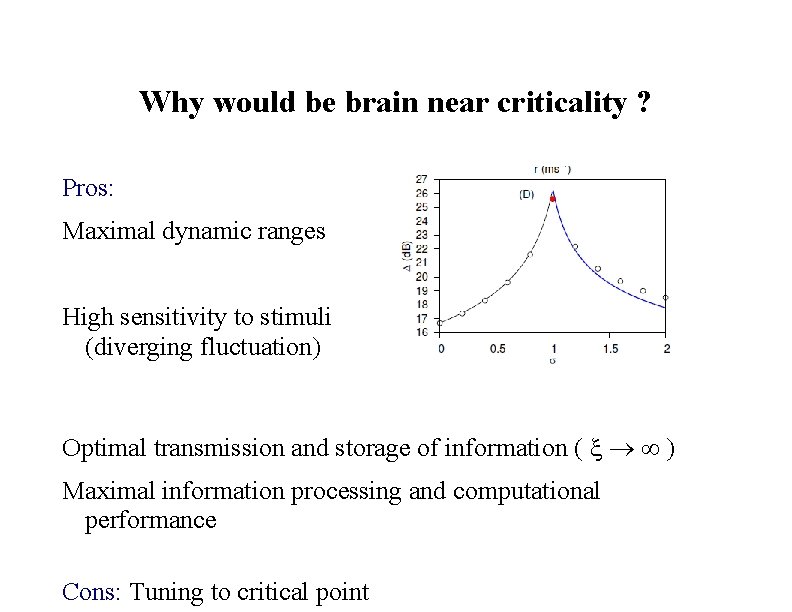
Why would be brain near criticality ? Pros: Maximal dynamic ranges High sensitivity to stimuli (diverging fluctuation) Optimal transmission and storage of information ( Maximal information processing and computational performance Cons: Tuning to critical point

What do we know about neuron networks ? Very little. The largest precisely explored structural networks contains 302 neurons (C. Elegans) Connectomes, obtained by approximative methods like diffusion MRI contain < 106 nodes (voxels) Unknown faithfulness, intensive research to automate image processing

Freely downloadable images and graphs of humans and animals

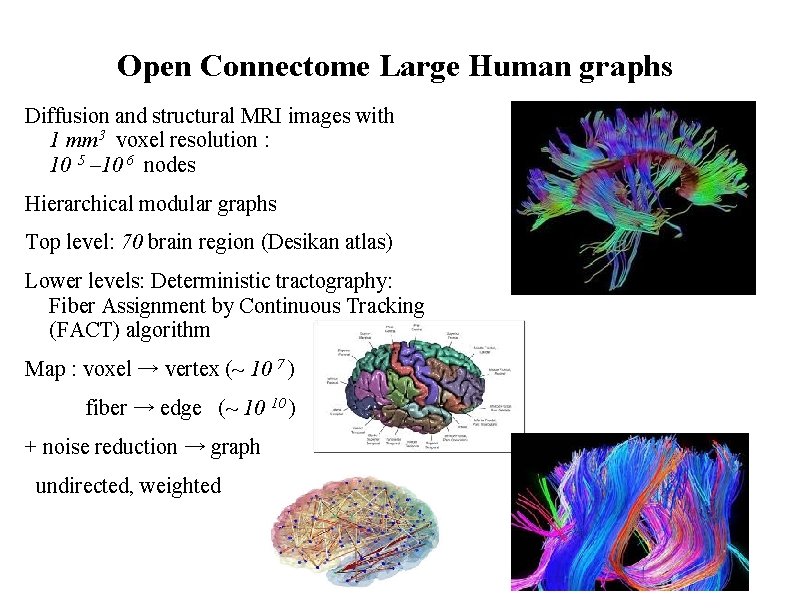
Open Connectome Large Human graphs Diffusion and structural MRI images with 1 mm 3 voxel resolution : 10 5 – 10 6 nodes Hierarchical modular graphs Top level: 70 brain region (Desikan atlas) Lower levels: Deterministic tractography: Fiber Assignment by Continuous Tracking (FACT) algorithm Map : voxel → vertex (~ 10 7 ) fiber → edge (~ 10 10 ) + noise reduction → graph undirected, weighted

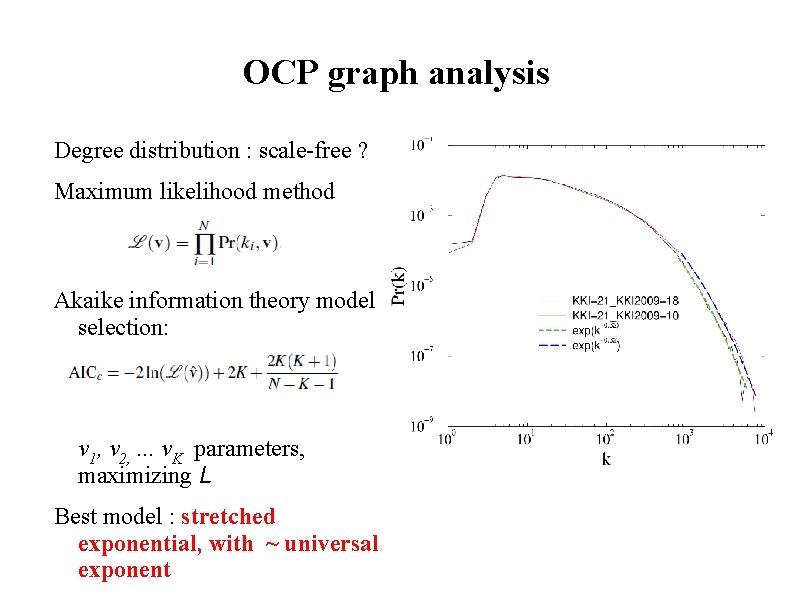
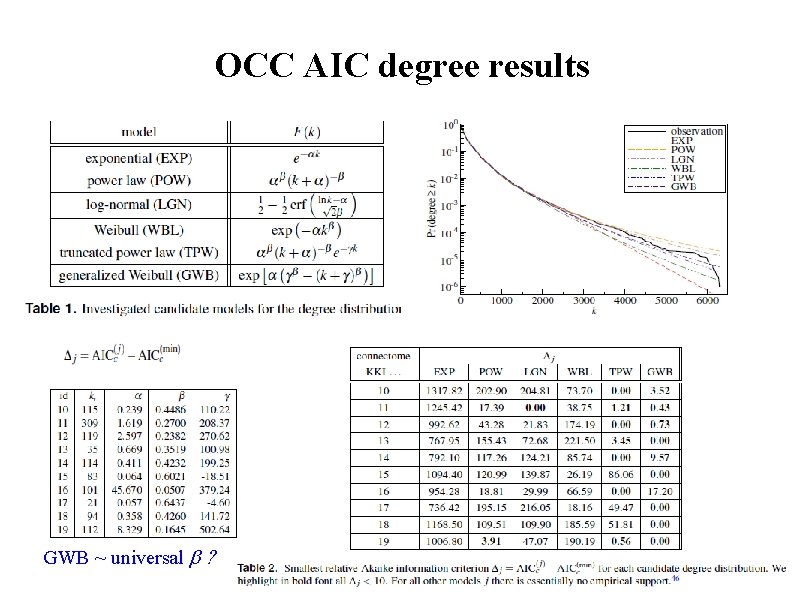
OCP graph analysis Degree distribution : scale-free ? Maximum likelihood method Akaike information theory model selection: v 1, v 2, . . . v. K parameters, maximizing L Best model : stretched exponential, with ~ universal exponent

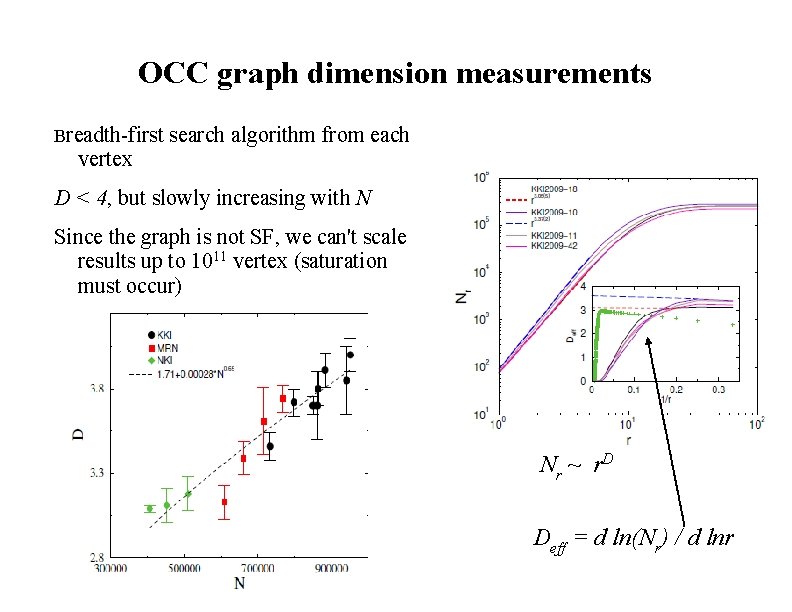
OCC graph dimension measurements Breadth-first search algorithm from each vertex D < 4, but slowly increasing with N Since the graph is not SF, we can't scale results up to 1011 vertex (saturation must occur) N r ~ r. D Deff = d ln(Nr) / d lnr

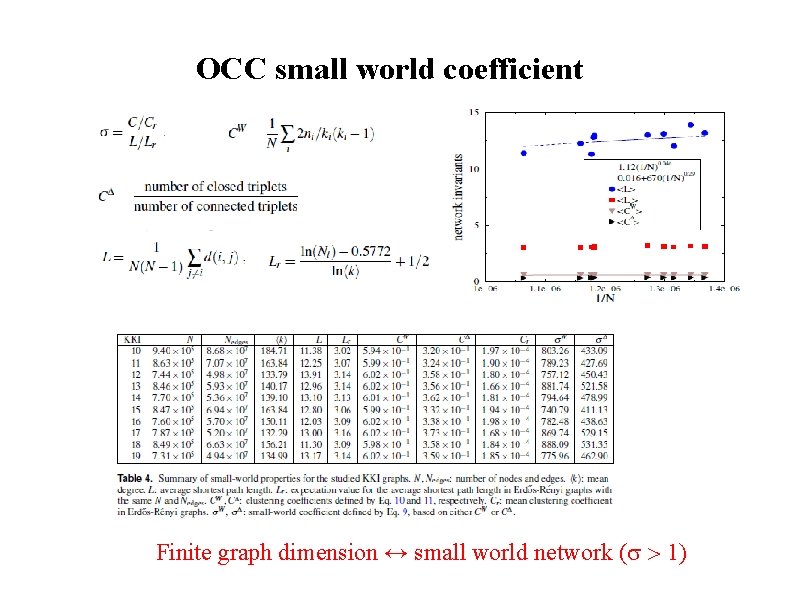
OCC small world coefficient Finite graph dimension ↔ small world network ( 1)

Further details in :

Threshold model simulations on an OCP graph KKI-18 graph: 836733 vertex, 8 x 107 weighted, undirected edges Cluster spreading simulations from randomly selected active nodes Survival probability: Does not show critical region, but discontinuous phase transition → Inherent disorder of KKI-18 can't round the phase transition, No Griffiths Phase, Hub effects! Relative Threshold model : incoming weights normalized by the sum : to model homogeneous sensitivity of nodes Inhibiton: randomly selected weights are flipped to negative (quenched)

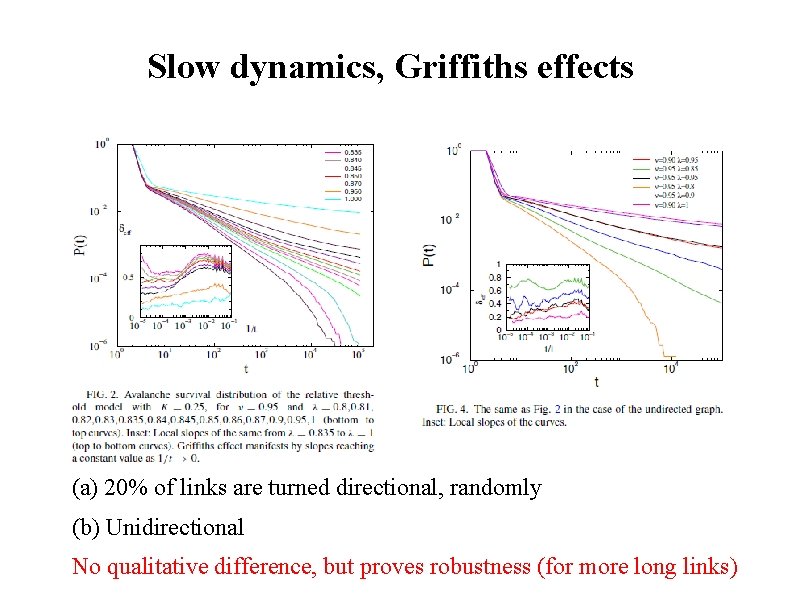
Slow dynamics, Griffiths effects (a) 20% of links are turned directional, randomly (b) Unidirectional No qualitative difference, but proves robustness (for more long links)

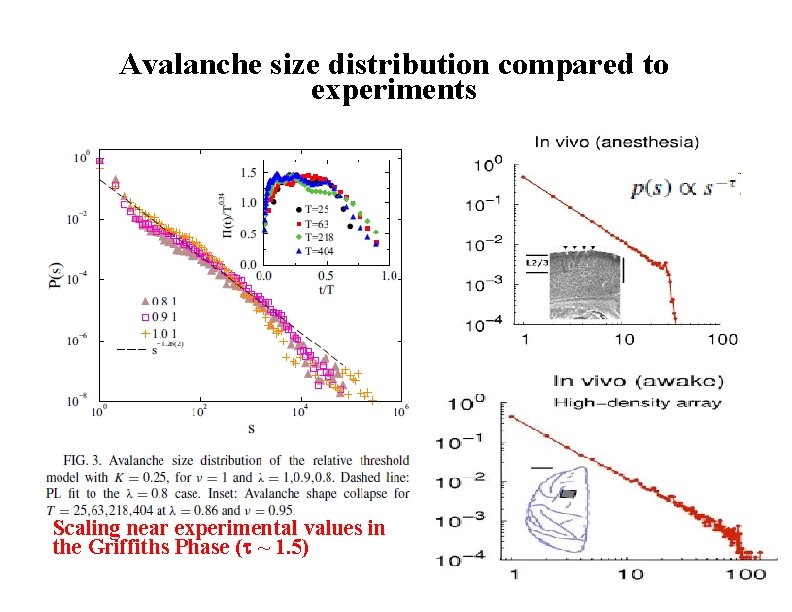
Avalanche size distribution compared to experiments Scaling near experimental values in the Griffiths Phase ( ~ 1. 5)

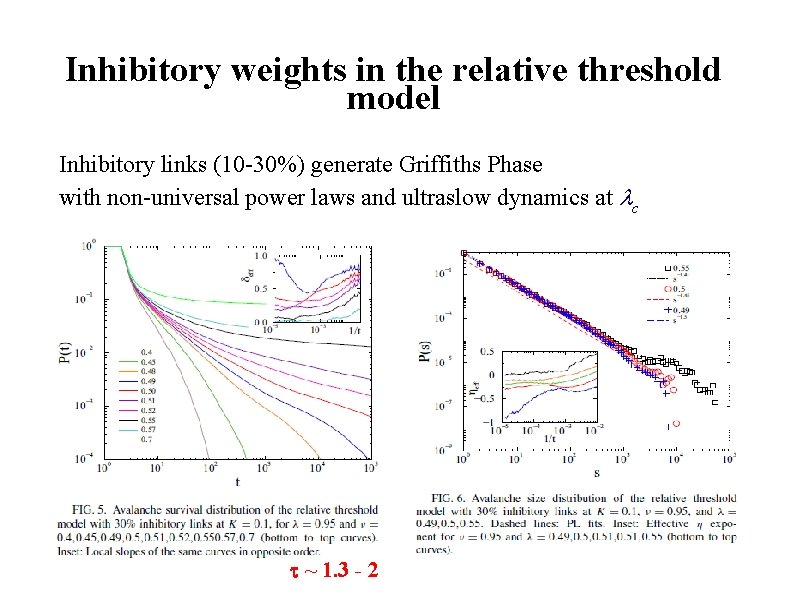
Inhibitory weights in the relative threshold model Inhibitory links (10 -30%) generate Griffiths Phase with non-universal power laws and ultraslow dynamics at c ~ 1. 3 - 2

Conclusions Heterogeneity effects are considered on large OCP connectomes using extremely large size simulations This enables us to distinguish from finite size rounding effects Small world networks ↔ Finite dimension → GP phase ? Large OCP graphs show ~ degree distribution universality In the threshold model hubs do not allow criticality and GP In the relative threshold model rare region effects are enhanced GP occurs with scaling exponents ~ experiments sub-critically ! Insensitivity to 20% link (mainly short) directed removal, robustness Quenched random inhibitory links do not fragment graph but cause GP effects and dynamical scaling sub-critically without SOC Power-laws in a single representative network (no sample avaraging) thanks to modular structure GÓ: PHYSICAL REVIEW E 94, 062411 (2016) Hungarian OTKA support

Biological parameters of neocortex

Firing of a group of neurons: biology vs model x 1 w 1: synaptic strength wn xn

Két kapcsolódó neuron

OCC AIC degree results GWB ~ universal

Rare Region theory for quench disordered CP Fixed (quenched) disorder/impurity „dirty critical point” changes the local birth rate c c Locally active, but arbitrarily large GP Rare Regions „clean critical point” in the inactive phase due to the inhomogeneities c Act. c Probability of RR of size LR: Abs. w(LR ) ~ exp (-c LR ) contribute to the density: (t) ~ ∫ d. LR LR w( LR ) exp [ -t / ( LR )] For c : conventional (exponentially fast) decay At c the characteristic time scales as: LR ) ~ LR Z ln (t) ~ t d / ( d + Z) For c 0 < < c : ��� (t) ~ t - c / b At c : b may diverge saddle point analysis: LR ) ~ exp(b LR ): stretched exponential Griffiths Phase continuously changing exponents (t) ~ ln(t Infinite randomness fixed point scaling GP: Dynamical (scaling) criticality + susceptibility diverges