critical Casimir forces and anomalous wetting Sbastien Balibar

critical Casimir forces and anomalous wetting Sébastien Balibar and Ryosuke Ishiguro Laboratoire de Physique Statistique de l ’Ecole Normale Supérieure, associé au CNRS et aux Universités Paris 6 & 7 Paris, France for references and files, go to http: //www. lps. ens. fr/~balibar/ Stat. Phys Bangalore, july 2004

abstract a critical introduction to and discussion of the "critical Casimir effect" "critical point wetting", i. e. wetting near a critical point 4 experiments: Garcia and Chan (Cornell, 1999) Ueno et al. (Kyoto, 2000) Ueno et al. (Paris, 2003) Ishiguro and Balibar (Paris, 2004)

the "critical Casimir effect" 2 plates confined fluctuations L the standard Casimir effect : confinement of the fluctuations of the electromagnetic field the two electrodes attract each other the critical Casimir effect (Fisher and de Gennes, 1978): near a critical point, confinement of the fluctuations of the order parameter a singular contribution to the free energy E ~ k. BT /L 2 a force between the two plates FCas = - d. E/d. L ~ 2 k. BT /L 3

the universal scaling functions Q and q Further work (Nightingale and J. Indekeu 1985, M. Krech and S. Dietrich 1991 -92) shows that E = k. BT/L 2 Q (L/x) where the "universal scaling function" Q depends on the bulk correlation function x ~ t -n which diverges near the critical temperature Tc. At Tc , i. e. t = 0, Q(0 = D , the "Casimir amplitude". a similar scaling function is introduced for the force FCas = k. BT/L 3 q (L/x)

Universality the scaling functions only depend on - the dimension of space - the dimension of the order parameter - the type of boundary conditions : - periodic or antiperiodic - Dirichlet - von Neumann the 5 different values D = Q (Tc) have been calculated, but not Q at any T nor with any boundary conditions for example Dirichlet-Dirichlet below Tc

the sign of the force attractive if symmetric boundary conditions (q < 0) repulsive if antisymmetric (q > 0) the Casimir amplitude D = Q (L/x = 0) ~ 0. 2 to 0. 3 for periodic boundary conditions proportional to the dimension N of the order parameter 10 times smaller if the order parameter vanishes at the wall (Dirichlet-Dirichlet) twice as large if tri-critical instead of critical

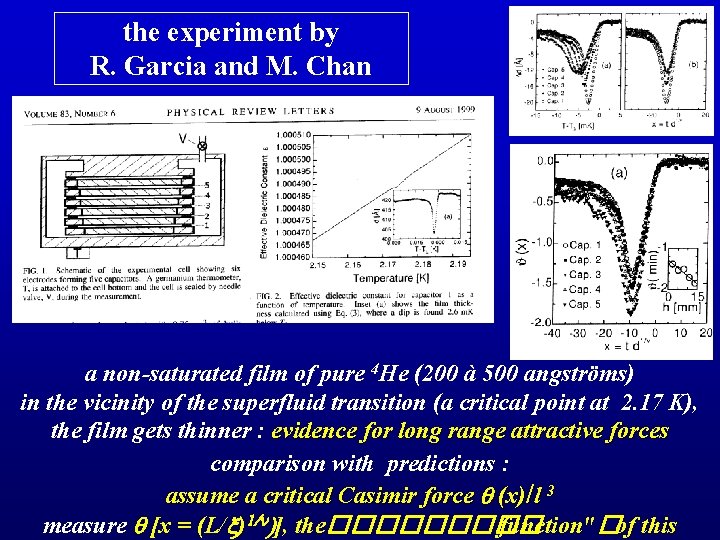
the experiment by R. Garcia and M. Chan a non-saturated film of pure 4 He (200 à 500 angströms) in the vicinity of the superfluid transition (a critical point at 2. 17 K), the film gets thinner : evidence for long range attractive forces comparison with predictions : assume a critical Casimir force q (x)/l 3 measure q [x = (L/x)1/n ], the����� function"�of this

comparison with theory above Tc : agreement with Krech and Dietrich [Phys. Rev. A 46, 1886 (1992)] below Tc : no theory the magnitude of the experimental q depends on L (not universal ? ? ) it is also surprisingly large (1. 5 to 2, no theoretical result larger than ~ 0. 5) far below Tc: a finite value of q ? confinement of Godstone modes (Ajdari et al. 1991, Ziherl et al. 2000, Kardar et al. 1991 -2004, Dantchev and Krech 2004)

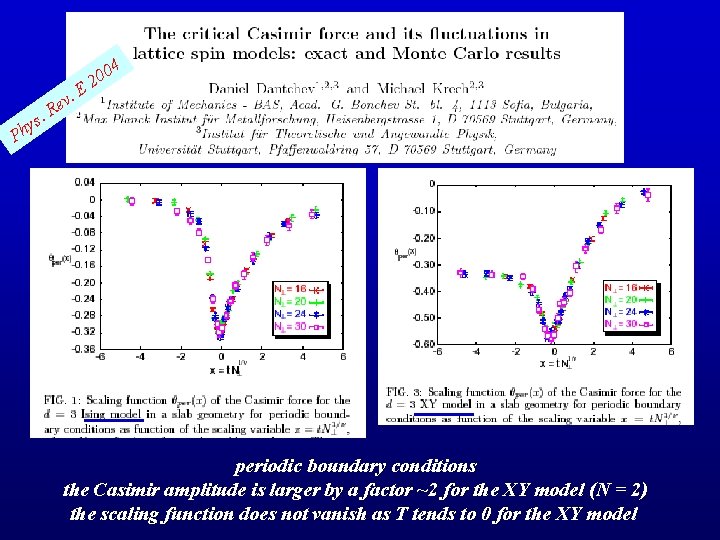
04 s. y h v. e R 0 2 E P periodic boundary conditions the Casimir amplitude is larger by a factor ~2 for the XY model (N = 2) the scaling function does not vanish as T tends to 0 for the XY model

the magnitude of the effect of Godstone modes for Dirichlet-Dirichlet boundary conditions, Kardar and Golestanian (Rev. Mod. Phys. 1999) predict a very small amplitude q ~ - 0. 05 Garcia's measurement : q ~ - 0. 3 in agreement with Dantchev (but with periodic boundary conditions) at the 2004 APS march meeting, R. Zandi, J. Rudnick and M. Kardar invoke the surface fluctuations of the film which would enhance the Goldstone mode contribution, but the sign of this last effect is somewhat controversial. In fact the situation is not settled: better experiments, and calculations with the right boundary conditions are needed

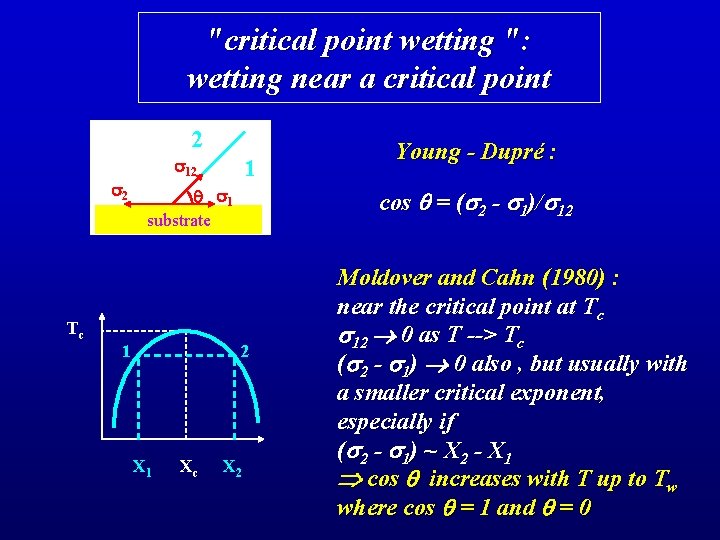
"critical point wetting ": wetting near a critical point 2 s 2 Tc s 12 1 q s 1 substrate 1 Xc cos q = (s 2 - s 1)/s 12 2 X 1 Young - Dupré : X 2 Moldover and Cahn (1980) : near the critical point at Tc s 12 0 as T --> Tc (s 2 - s 1) 0 also , but usually with a smaller critical exponent, especially if (s 2 - s 1) ~ X 2 - X 1 cos q increases with T up to Tw where cos q = 1 and q = 0

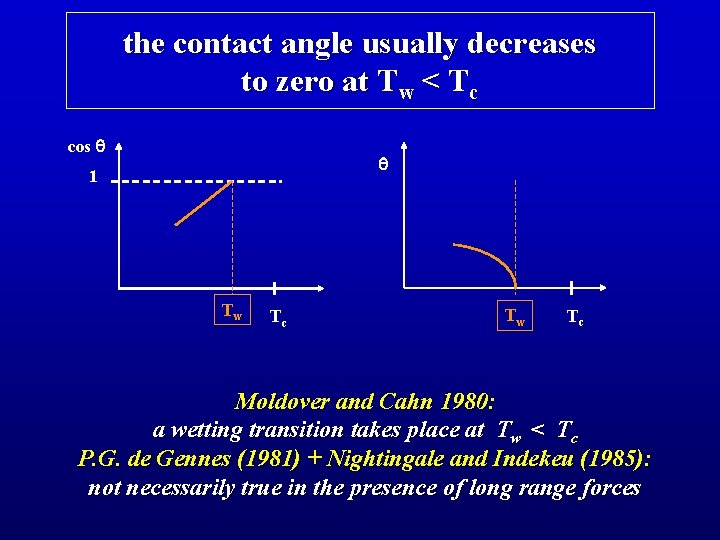
the contact angle usually decreases to zero at Tw < Tc cos q q 1 Tw Tc Moldover and Cahn 1980: a wetting transition takes place at Tw < Tc P. G. de Gennes (1981) + Nightingale and Indekeu (1985): not necessarily true in the presence of long range forces

a possible exception to critical point wetting the example of helium 3 - helium 4 liquid mixtures T normal superfluid 0. 87 K tri-critical point a tri-critical point: superfluidity + phase separation at Tt = 0. 87 K 0 0. 675 3 He concentration 1

a 4 He-rich superfluid film Romagnan, Laheurte and Sornette (1978 - 86): van der Waals attractive field a 4 He-rich film grows on the substrate 4 He-rich normal T superfluid Teq superfluid film leq tri-critical point substrate leq ~ (T - Teq)-1/3 up to 60 Angstöms two possibilities: - van der Waals only, leq tends to a macroscopic value: complete wetting (q = 0) - vd. W + an attractive force (Casimir), leq saturates at some mesoscopic value: partial wetting (q ≠ 0) 0 1 3 He concentration superfluid film 4 He-rich bulk phase q substrate leq

an approximate calculation the contact angle q is obtained from the "disjoining pressure" P (l) (see Ueno, Balibar et al. PRL 90, 116102, 2003 and Ross, Bonn and Meunier, Nature 1999): 3 contributions to P (l) from long range forces: van der Waals (repulsive on the film surface) Casimir (attractive) Q (l/x) < 0 is the scaling function which can be estimated from Garcia and Chan the entropic or "Helfrich" repulsion due to the limitation of the fluctuations of the film surface

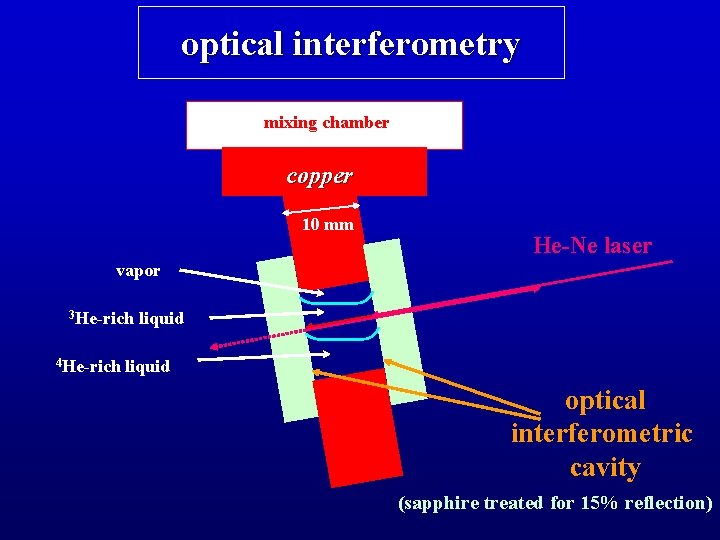
optical interferometry mixing chamber copper 10 mm He-Ne laser vapor 3 He-rich 4 He-rich liquid optical interferometric cavity (sapphire treated for 15% reflection)

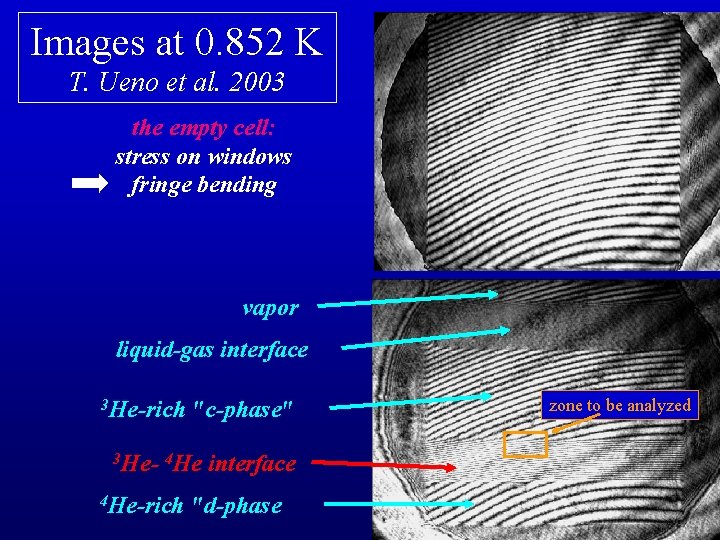
Images at 0. 852 K T. Ueno et al. 2003 the empty cell: stress on windows fringe bending vapor liquid-gas interface 3 He-rich "c-phase" 3 He- 4 He interface 4 He-rich "d-phase zone to be analyzed

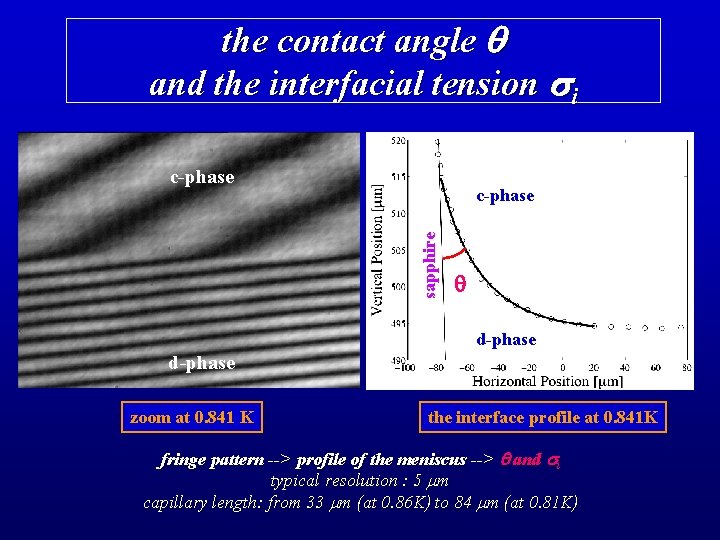
the contact angle q and the interfacial tension si c-phase sapphire c-phase q d-phase zoom at 0. 841 K the interface profile at 0. 841 K fringe pattern --> profile of the meniscus --> q and si typical resolution : 5 mm capillary length: from 33 mm (at 0. 86 K) to 84 mm (at 0. 81 K)

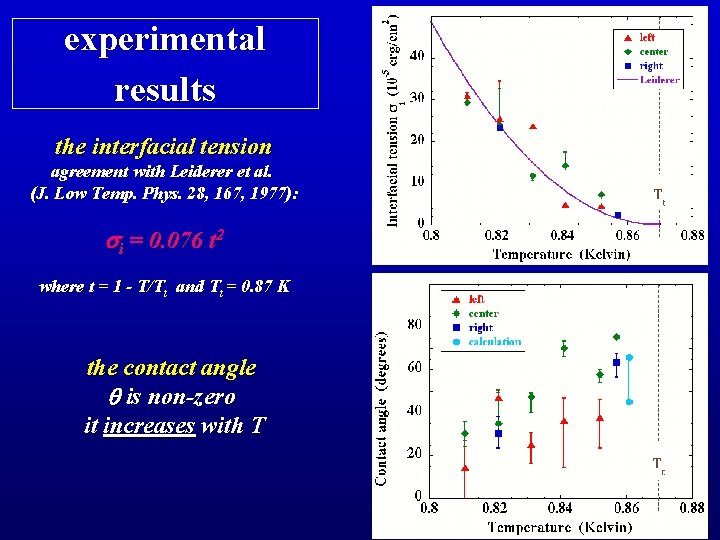
experimental results the interfacial tension agreement with Leiderer et al. (J. Low Temp. Phys. 28, 167, 1977): si = 0. 076 t 2 where t = 1 - T/Tt and Tt = 0. 87 K the contact angle q is non-zero it increases with T

the disjoining pressure at 0. 86 K (i. e. t = 10 -2) the equilibrium thickness of the superfluid film: leq = 400 Å ~ about 4 x , where P (l) = 0

the calculated contact angle q at T = 0. 86 K, i. e. t = 1 - T/Tt = 10 -2 leq = 400 Å , 4 times the correlation length x By integrating the disjoining pressure from leq to infinity, we find q = 45 ° near a tri-critical point, the Casimir amplitude should be larger by a factor 2 this would lead to q = 66 °, in even better agreement with our experiment At lower temperature (away from Tt ): si and van der Waals are larger, Casimir is smaller, so that q should also be smaller the contact angle increases with T, as found experimentally

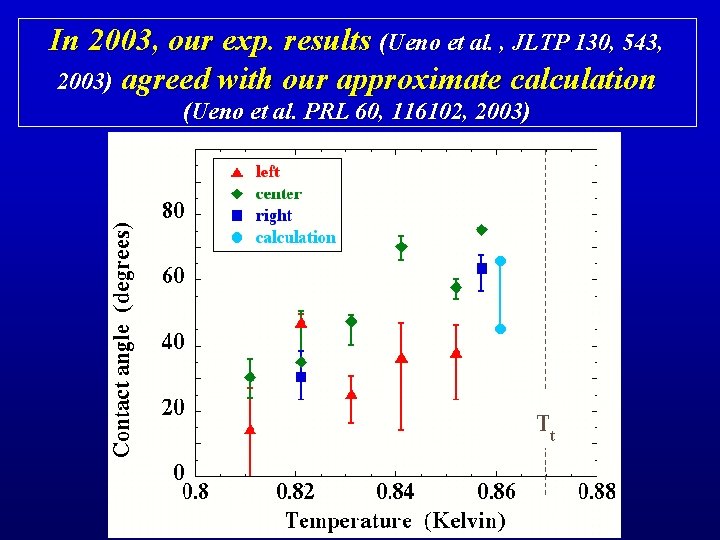
In 2003, our exp. results (Ueno et al. , JLTP 130, 543, 2003) agreed with our approximate calculation (Ueno et al. PRL 60, 116102, 2003)

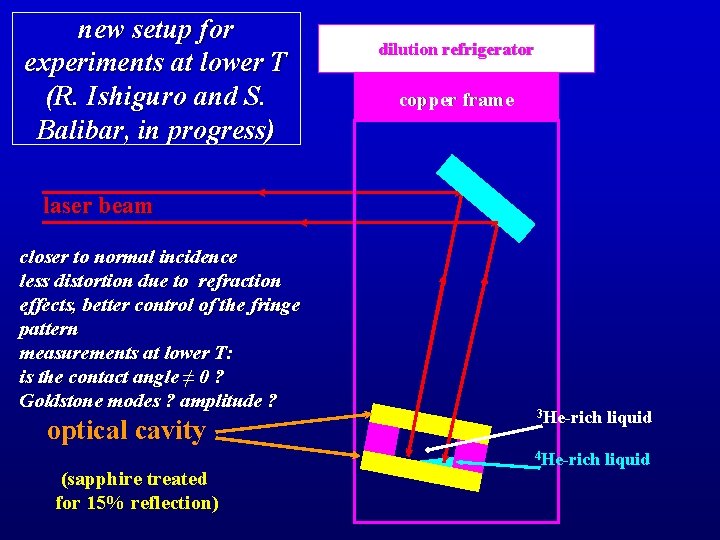
new setup for experiments at lower T (R. Ishiguro and S. Balibar, in progress) dilution refrigerator copper frame laser beam closer to normal incidence less distortion due to refraction effects, better control of the fringe pattern measurements at lower T: is the contact angle ≠ 0 ? Goldstone modes ? amplitude ? optical cavity (sapphire treated for 15% reflection) 3 He-rich liquid 4 He-rich liquid

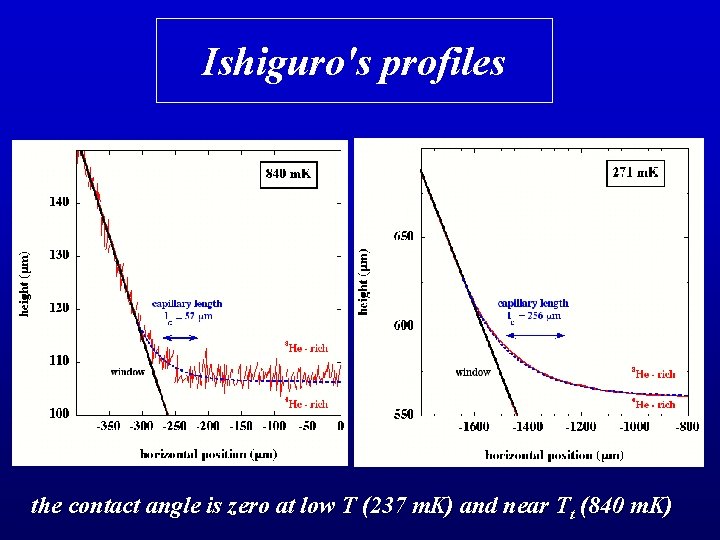
Ishiguro's profiles the contact angle is zero at low T (237 m. K) and near Tt (840 m. K)

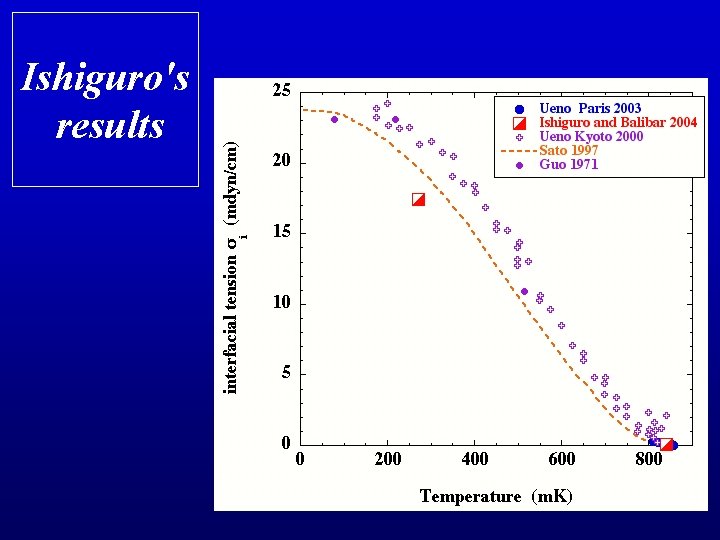
Ishiguro's results

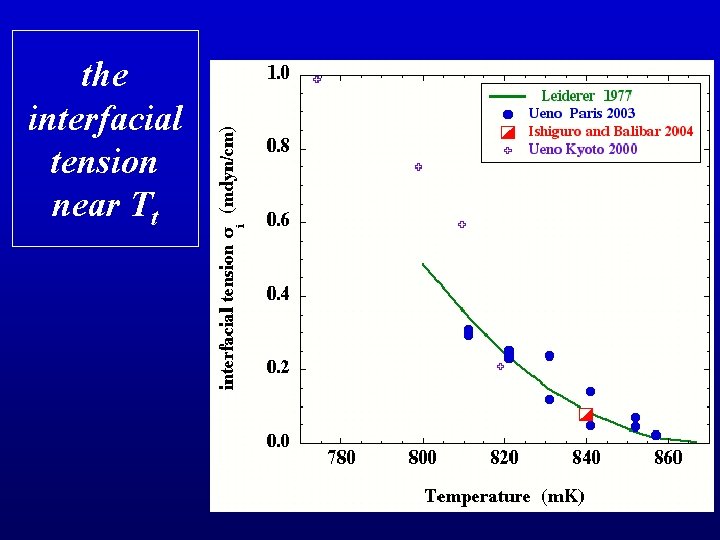
the interfacial tension near Tt

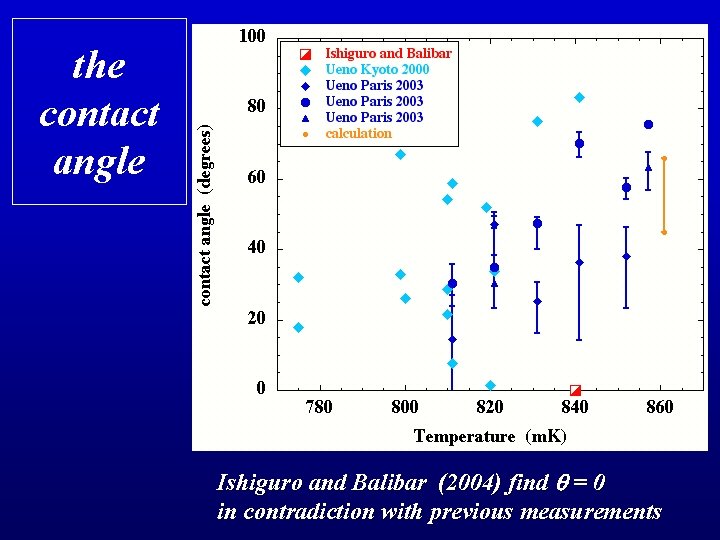
the contact angle Ishiguro and Balibar (2004) find q = 0 in contradiction with previous measurements

could the Casimir force be 5 times smaller than measured by Garcia and Chan ? the disjoining pressure would be dominated by the van der Waals field, always positive, implying complete wetting (q = 0)

summary the exception found by Ueno et al. to "critical point wetting" is not confirmed by our more careful, and more recent experiment still possible if the substrate exerted a weaker van der waals field ? the amplitude of the critical Casimir force measured by Garcia and Chan is not really universal and its amplitude looks large but there is no available calculation with the right boundary conditions below Tc where it is large. more work. . .