CPT 450 Computer Graphics Lecture 11 Homogenous Coordinates

CPT 450 – Computer Graphics Lecture 11 – Homogenous Coordinates

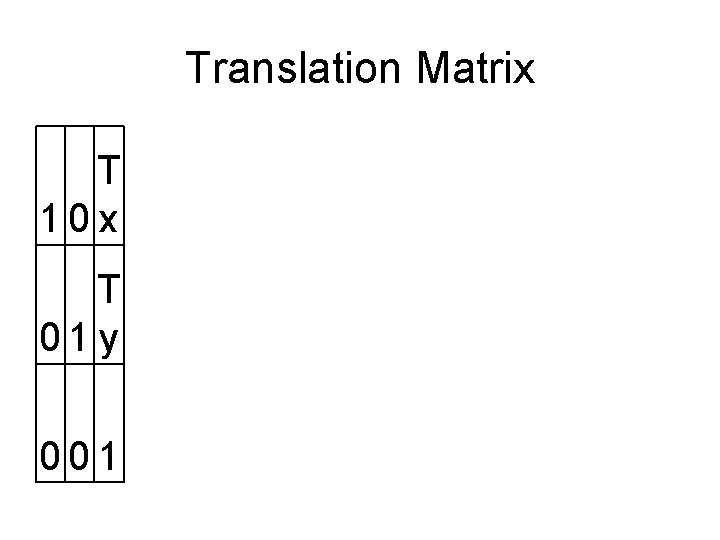
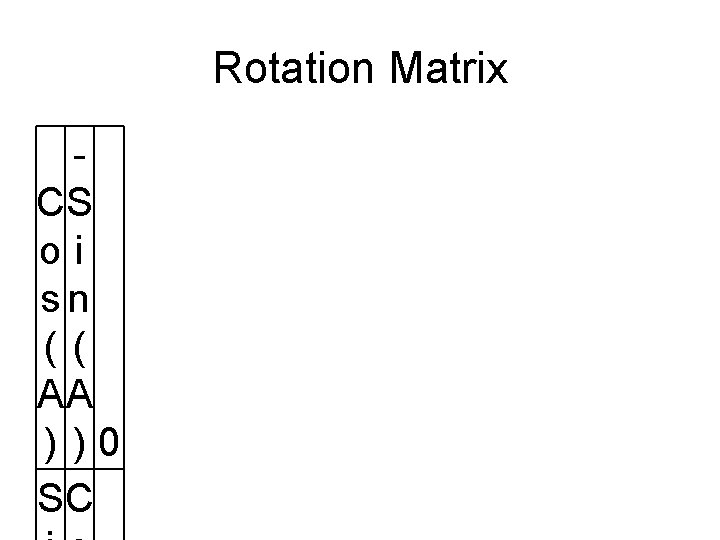
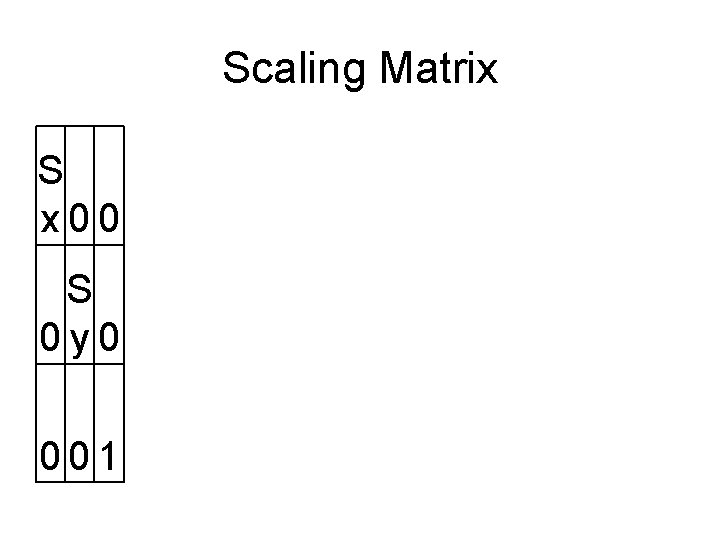
Basic Transformations • Translation by (Tx, Ty) X’ = X + Tx Y’ = Y + Ty • Scaling by Sx in X and Sy in Y about origin – Note: Reflection is a special case where Sx = +/-1, Sy = +/-1 X’ = X * Sx Y’ = Y * Sy • Rotation (about origin by angle A) X’ = X*cos(A) – Y*sin(A) Y’ = X*sin(A) + Y*cos(A) • It would be nice if we could do all of these operations using the same equations…

Geometric versus Coordinate Transformations • Schaum’s Outlines on Computer Graphics (p. 74) differentiates between the Geometric Transformations and the Coordinate Transformations. They are inverse functions. – Geometric transformations assume that the object is transformed and the coordinate system is fixed. – Coordinate transformations assume that the coordinate system changes and the object is fixed. • For example – Translation: Geometric transformations use (Tx, Ty) where as coordinate transformations use (-Tx, -Ty) – Scaling: Geometric transformations use Sx and Sy where as coordinate transformations use 1/Sx and 1/Sy. – Rotation: geometric use A where as coordinate transformations use (-A). Remember cos(-a) = cos(a) and sin(-a) = -sin(a) – Reflections are unchanged, due to symmetry. • Note: Sign conventions are important. If you’re not sure, use a trivial example, i. e. let the angle =90 or the scale = 2.

Homogeneous Coordinates • Idea: We introduce an extra coordinate, which we will set to 1. • Therefore, the 2 D point [x, y] T is represented as [x, y, 1] T in homogeneous coordinates. • This is equivalent to [c*x, c*y, c] T, where c is a non-zero constant. Usually it is written in normalized form, so that the last coordinate is 1. • Homogeneous coordinates allow us to express each of these transformations as a matrix multiplication. • Computers can perform these matrix calculations very quickly in software and even faster in hardware.

Homogenous Coordinates • Beware! – Some books (such as Schaum’s Outlines, Foley) represent points as column vectors [x, y, 1] T , where T = transposed and other books (and computer graphics literature) represent points as row vectors [x, y, 1]. • Matrix multiplication. Note: order is different and the matrix gets transposed. – Column vector representation. • [x 2, y 2, 1] T= [x 1, y 1, 1] T * M T – Row vector representation • [x 2, y 2, 1] = M * [x 1, y 1, 1] • I will represent points as column vectors.

Matrix Multiplication, Vectors & Matrices • Some books do it one way, others do it the other way. • New Column Vector = Matrix * Column Vector V’ = M x V, V = [x, y, z] T V’(i) = M(i, 1)*V(1) + M(i, 2)*V(2) + M(i, 3)*V(3) • New Row Vector * Matrix = new Row Vector V’ = V x M’, V = [x, y, z] V’(i) = V(1)*M’(1, i) + V(2)*M’(2, i) + V(3)*M’(3, i) • Note: The matrices are transposed, i. e. M’ = M T

Multiplying Matrices, in general • C[m, n]=A[m, l] * B[l, n], where the size of the matrices are in brackets [#rows, #cols]. – Note: #cols in A = #rows in B For i = 0 to m - 1 For j = 0 to n - 1 C(i, j) = 0 For k = 0 to l - 1 C(i, j) += A(i, k) * B(k, j) Next k Next j Next i

Translation Matrix T 10 x T 01 y 001

Matrix Multiplication • Associative A*(B*C) = (A*B)*C • Not Commutative A*B <> B*A • Order matters M 2 = M*X (Append) M 2 = X*M (Prepend)

Rotation Matrix CS oi sn (( AA ) )0 SC

Scaling Matrix S x 00 S 0 y 0 001

Matrix Multiplication Example Cos(90) -Sin(90) = X Sin(90) Cos(90) 0 0 -20 10 0 0 20 10 1 1 1