CPSC 320 Intermediate Algorithm Design and Analysis July

CPSC 320: Intermediate Algorithm Design and Analysis July 2, 2014 1

Instructor and Course Structure 2

Instructor Jonatan Schroeder jonatan@cs. ubc. ca Office: ICICS/CS 247 Office hours: • Mon/Wed/Fri: 12 -1 pm • Or by appointment 3

Teaching Assistants • • • Alireza Shafaei Anupam Srivastava Jianing Yu Juyoung Moon Reza Babanezhad 4

Pre-requisites • Listed student numbers should come to me after class • If you fail to act, you may be dropped from the course • Walk-in advising hours: • Today 4 -5 pm: ICCS 391 (Paul Carter) • Thu 10: 30 -11: 30 am: ICCS 391 (Paul Carter) • Thu 3 -4 pm: ICCS 307 (George Tsiknis) • Additional hours may be listed in front of CS main office 5

Learning Goals • Understand techniques used to design efficient algorithms • Prove (or disprove) that designed algorithms are correct • Prove that designed algorithms are efficient 6

Course Outline • • • Introduction and basic concepts Asymptotic notation Greedy algorithms Graph theory Amortized analysis Recursion Divide-and-conquer algorithms Randomized algorithms Dynamic programming algorithms NP-completeness 7

Schedule • Lectures: Mon/Wed/Fri 9: 30 -12: 00 • Tutorials: • T 2 A: Wed/Fri 1 -2 pm (Anupam) • T 2 B: Wed/Fri 2 -3 pm (Anupam) • T 2 C: Wed/Fri 3 -4 pm (Alireza) 8

Piazza • All course announcements will be posted on Piazza • All course-related questions should be asked on Piazza • Instructors and TAs will direct your questions to Piazza when relevant • Questions including part of a possible solution should be made private • Instructors may change a private question to public if deemed useful for other students • Students are encouraged to answer questions as well 9

Piazza (continued) • Please take a minute to understand how Piazza works • Students’ response is for answering questions, not follow -ups • Remember to mark follow-ups as resolved • If you found the answer on your own, please add an answer (don’t delete the question) 10

Marking scheme • 6 or 7 assignments: 20% • 5 quizzes: 30% • Final exam: 50% • You must pass the exam to pass the course • You must pass in the average of the quizzes • You must submit at least five of the assignments 11

Assignments • 6 or 7 assignments • Electronic submission or physical copy submission? • Please answer a poll on Piazza today before 6 PM!!! • Assignment 1 will be posted some time today 12

Quizzes • • • Quiz 1: Wed, July 9 Quiz 2: Wed, July 16 Quiz 3: Wed, July 23 Quiz 4: Wed, July 30 Quiz 5: Wed, August 6 • Closed book, closed notes, no calculator • Individual component: about 30 minutes • Group component: about 15 minutes • The group component is to be done in groups of 3 -4 • Group will solve one of the questions in the individual component 13

Textbook • John Kleinberg and Éva Tardos, Algorithm Design, Addison. Wesley Publishing company, 2005, ISBN 0 -321 -29535 -8. • Optional: Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein, Introduction to Algorithms, 3 rd edition, MIT Press, 2009, ISBN 0 -262 -03384 -4. 14

Representative Problem The Stable Matching Problem 15

Algorithm • • Sequence of steps to solve a specific task or problem Takes an input, provides a result Each step depends solely on the input and on previous steps Stops in finite time 16

Algorithm Analysis • • • Does the algorithm terminate? How long does it take (as a function of the input size)? Does it produce a valid result? Is the produced result correct? Is the produced result optimal? 17

Stable Matching Problem • 18

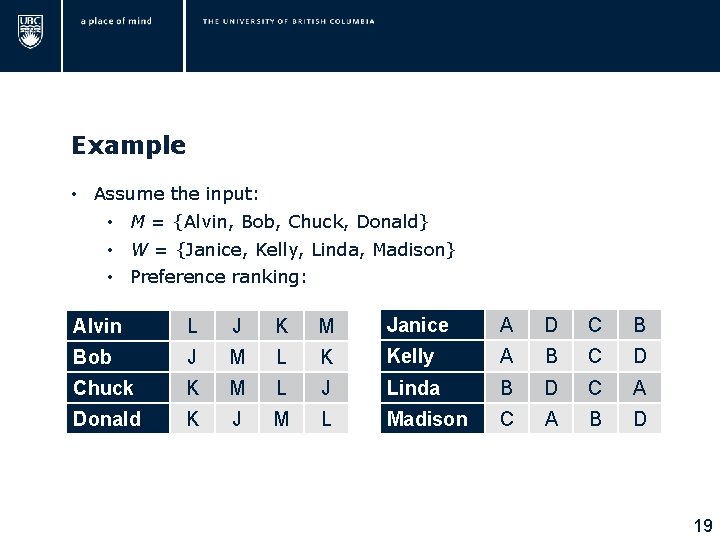
Example • Assume the input: • M = {Alvin, Bob, Chuck, Donald} • W = {Janice, Kelly, Linda, Madison} • Preference ranking: Alvin L J K M Janice A D C B Bob J M L K Kelly A B C D Chuck K M L J Linda B D C A Donald K J M L Madison C A B D 19

Example • Example matching: (A, L), (B, J), (C, K), (D, M) • Unstable (D prefers J, J prefers D) Alvin L J K M Janice A D C B Bob J M L K Kelly A B C D Chuck K M L J Linda B D C A Donald K J M L Madison C A B D 20

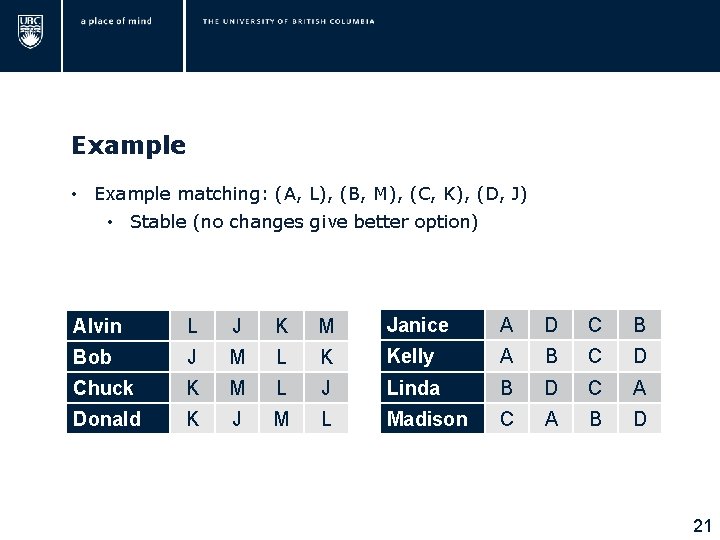
Example • Example matching: (A, L), (B, M), (C, K), (D, J) • Stable (no changes give better option) Alvin L J K M Janice A D C B Bob J M L K Kelly A B C D Chuck K M L J Linda B D C A Donald K J M L Madison C A B D 21

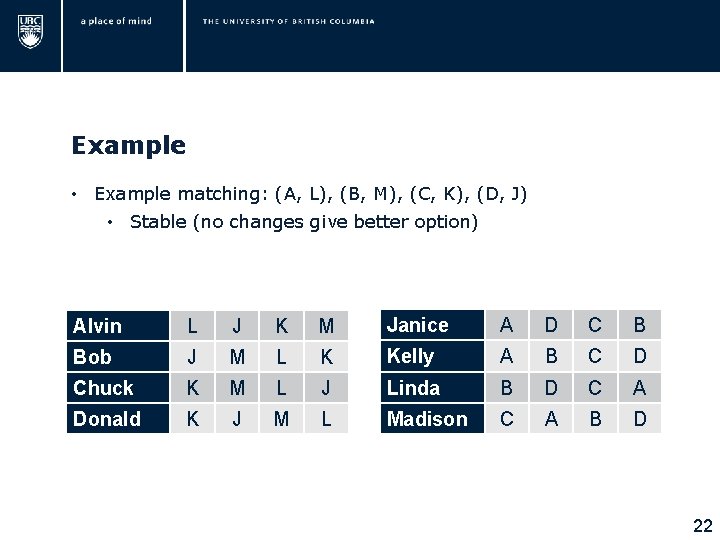
Example • Example matching: (A, L), (B, M), (C, K), (D, J) • Stable (no changes give better option) Alvin L J K M Janice A D C B Bob J M L K Kelly A B C D Chuck K M L J Linda B D C A Donald K J M L Madison C A B D 22

Discussion • What strategies can be used to find a matching? • Is there an optimal solution? • What defines optimal in this case? • Design an algorithm 23

Gale-Shapley Algorithm • 24

What should we do now? • Does the algorithm produce a matching? • Result includes every woman and every man? • Each woman is assigned to exactly one man? • Each man is assigned to exactly one woman? • Is the matching stable? • How long (in the worst case) does the algorithm take to terminate? 25

Complexity • Does the algorithm terminate? • What happens to a man m as the algorithm progresses? • How many times can a man get engaged? • What happens to a woman w as the algorithm progresses? • How many times can a woman get engaged? • What happens overall as the algorithm progresses? 26

Complexity • 27

Complexity (discussion) • 28

Correctness: Is the result a matching? • Does the resulting matching include every woman? • Every man, once engaged, is always engaged • If there is a free woman, there is a free man • Free woman will find a free man • Is each man engaged to one woman only? • If a man is free during proposal, he will be engaged to one woman • If a man is not free, he may replace one woman for another • Is each woman engaged to one man only? • Only free women propose 29

Correctness: Is matching stable? • 30

Correctness: Is matching stable? • 31

Correctness: Is matching stable? • 32

Correctness: Is matching stable? • 33

Discussion • Is the result optimal? • What is considered optimal? • Who gets it better, women or men? • How could this be changed? 34

Equivalent problems • Matching students and co-op jobs • Matching medical students and hospitals • Matching potential students and college openings 35

Variations and Similar Problems • • • Hospitals can take several students Number of men and women is different Restrictions and limited preference lists Stable roommate problem (matched pairs from same set) Hospital/student matching with couples Taxis and customers (reduced cost of pick up) 36

Asymptotic Notation 37

Machine Model • In all algorithms we will assume: • Sequential execution • One processor • Memory position can hold arbitrarily large integer • Unless otherwise specified, we will discuss the worst case • Best case: usually not very useful • Average case: depends on input distribution assumptions 38

Upper Bound • 39