Cpr E 281 Digital Logic Instructor Alexander Stoytchev

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Boolean Algebra Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • HW 1 is due today

Administrative Stuff • HW 2 is out • It is due on Wednesday Sep 6 @ 4 pm. • Submit it on paper before the start of the lecture

Boolean Algebra • An algebraic structure consists of § a set of elements {0, 1} § binary operators {+, } § and a unary operator { ’ } or { } • Introduced by George Boole in 1854 George Boole 1815 -1864 • An effective means of describing circuits built with switches • A powerful tool that can be used for designing and analyzing logic circuits

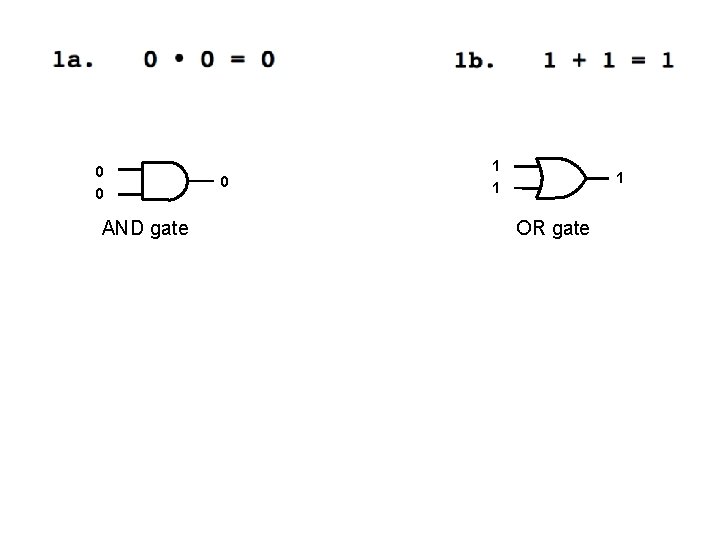
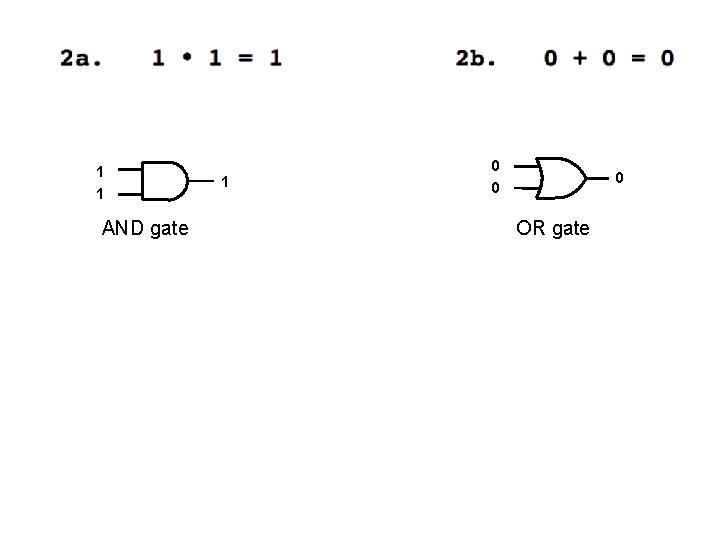
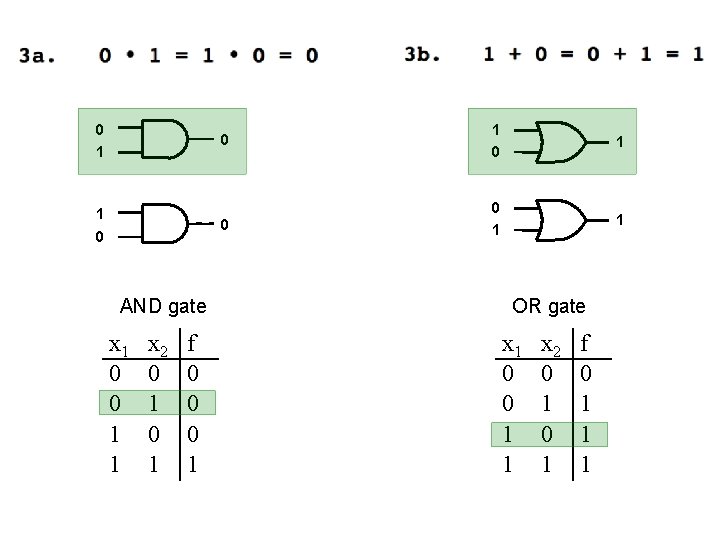
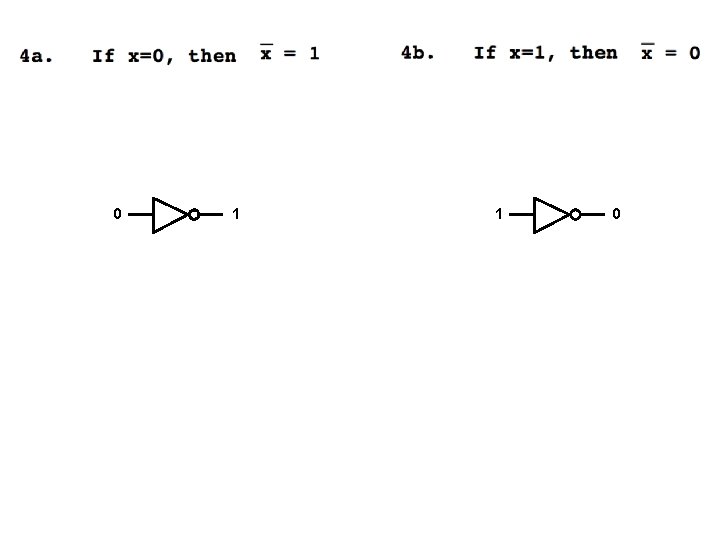
Axioms of Boolean Algebra 1 a. 0 0 = 0 1 b. 1 + 1 = 1 2 a. 1 1 = 1 2 b. 0 + 0 = 0 3 a. 0 1 = 1 0 = 0 3 b. 1 + 0 = 0 + 1 = 1 4 a. If x=0, then 4 b. If x=1, then x=1 x=0

Single-Variable Theorems 5 a. x 0 = 0 5 b. x + 1 = 1 6 a. x 1 = x 6 b. x + 0 = x 7 a. x x = x 7 b. x + x = x 8 a. x 8 b. x + 9. x=x x=0 x=1

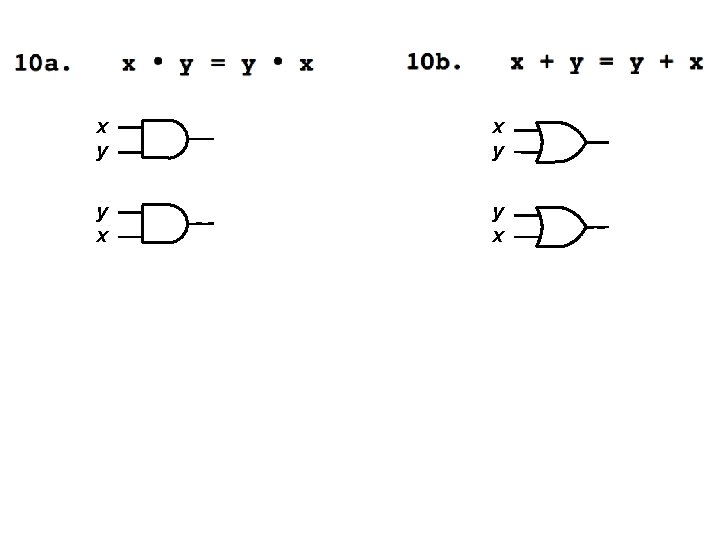
Two- and Three-Variable Properties 10 a. x y = y x 10 b. x + y = y + x Commutative 11 a. x (y z) = (x y) z 11 b. x + (y + z) = (x + y) + z Associative 12 a. x (y + z) = x y + x z 12 b. x + y z = (x + y) (x + z) Distributive 13 a. x + x y = x 13 b. x (x + y) = x Absorption

Two- and Three-Variable Properties 14 a. x y + x 14 b. (x + y) (x + y=x y) = x 15 a. x y = x + y 15 b. x + y = x y Combining De. Morgan’s theorem 16 a. x + x y = x + y 16 b. x (x + y) = x y 17 a. x y + y z + x z = x y + x z 17 b. (x+y) (y+z) (x+z)=(x+y) (x+z) Consensus

Now, let’s prove all of these

The First Four are Axioms (i. e. , they don’t require a proof) 1 a. 0 0 = 0 1 b. 1 + 1 = 1 2 a. 1 1 = 1 2 b. 0 + 0 = 0 3 a. 0 1 = 1 0 = 0 3 b. 1 + 0 = 0 + 1 = 1 4 a. If x=0, then 4 b. If x=1, then x=1 x=0

But here are some other ways to think about them

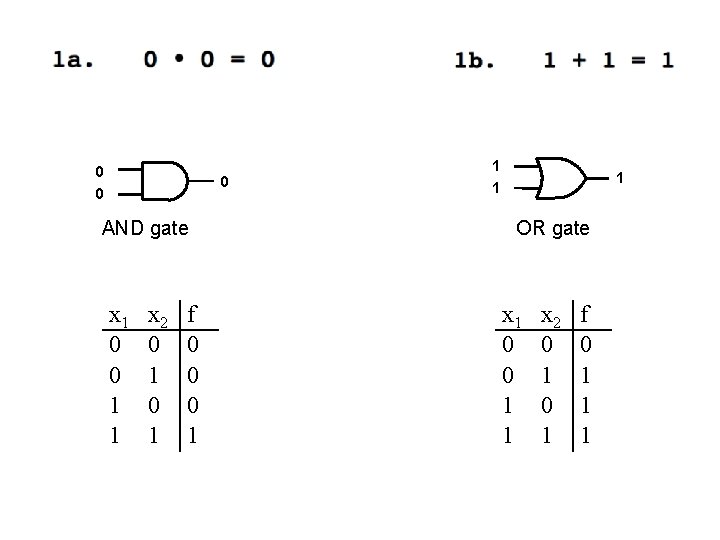
0 0 AND gate 0 1 1 1 OR gate

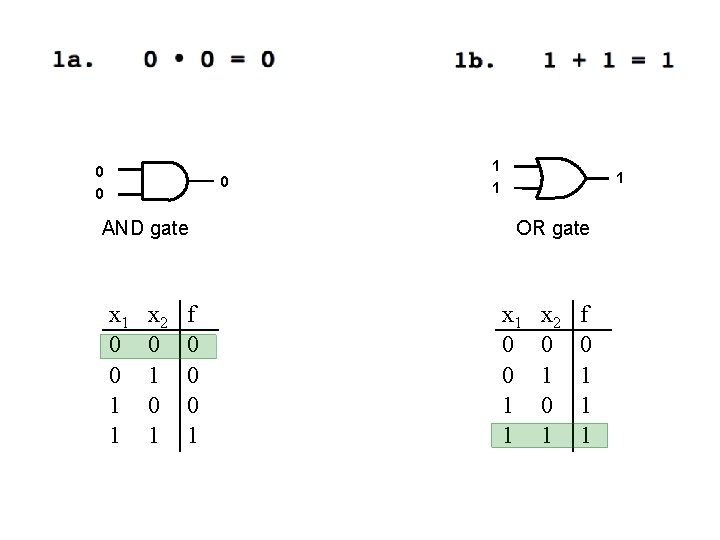
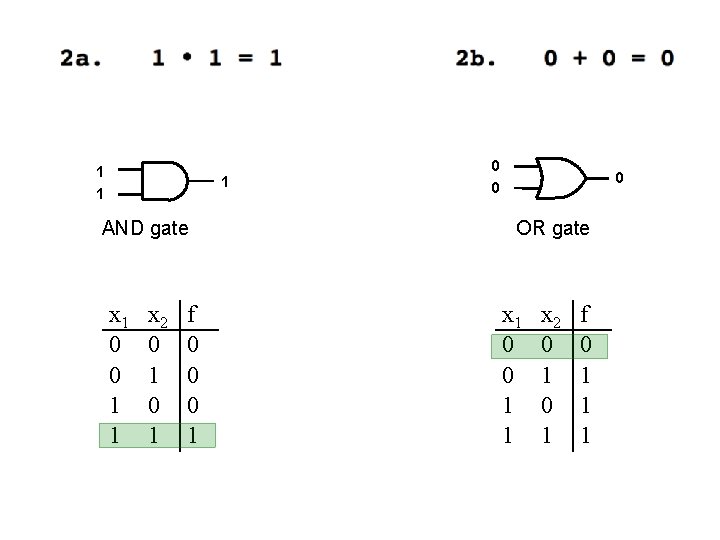
0 0 0 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 1 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

0 0 0 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 1 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

1 1 AND gate 1 0 0 0 OR gate

1 1 1 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 0 0 0 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

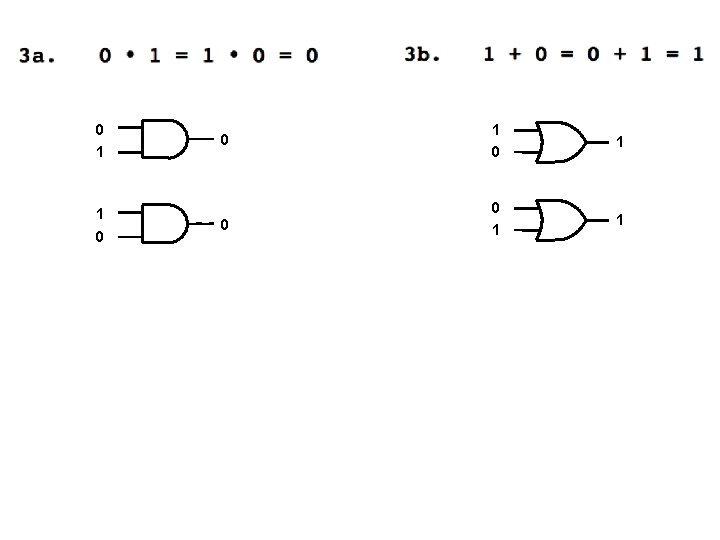
0 1 1 0 0 1 1

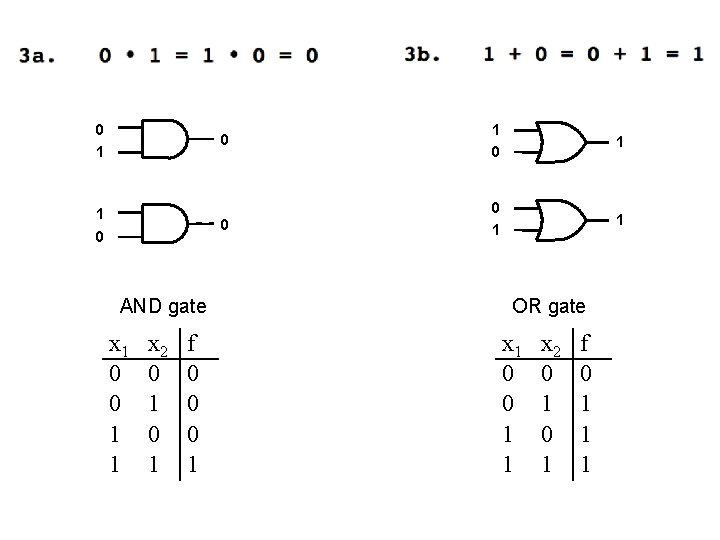
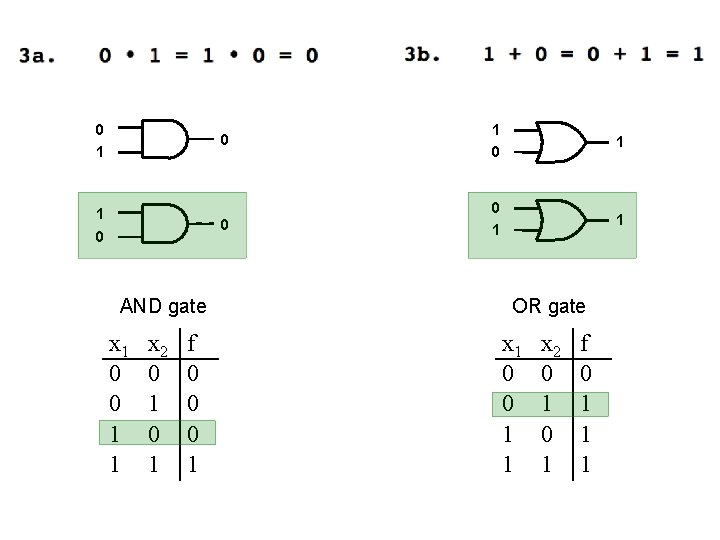
0 1 1 0 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 0 1 0 0 1 1 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

0 1 1 0 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 0 1 0 0 1 1 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

0 1 1 0 AND gate x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 0 1 0 0 1 1 OR gate x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

0 1 1 0

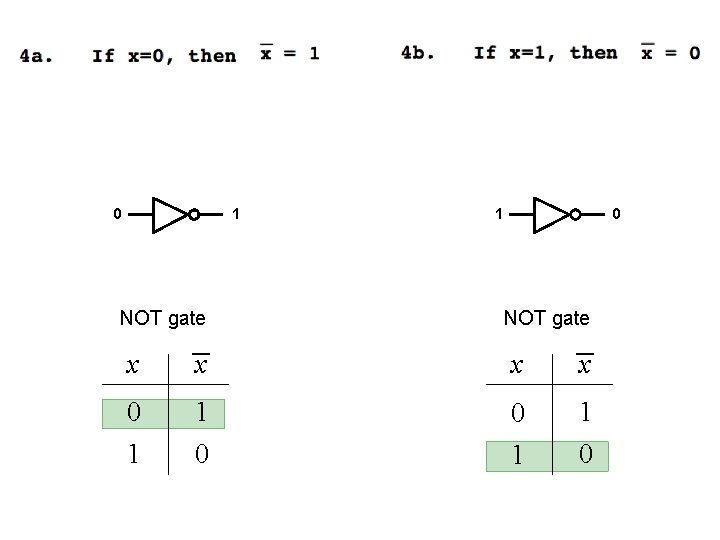
0 1 NOT gate 1 0 NOT gate x x 0 1 1 0

Single-Variable Theorems 5 a. x 0 = 0 5 b. x + 1 = 1 6 a. x 1 = x 6 b. x + 0 = x 7 a. x x = x 7 b. x + x = x 8 a. x 8 b. x + 9. x=x x=0 x=1

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately.

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0 0 = 0 // axiom 1 a

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0 0 = 0 // axiom 1 a ii) If x = 1, then we have 1 0 = 0 // axiom 3 a

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0+1 = 1 // axiom 3 b

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0+1 = 1 // axiom 3 b ii) If x = 1, then we have 1+1 = 1 // axiom 1 b

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0 1 = 0 // axiom 3 a ii) If x = 1, then we have 1 1 = 1 // axiom 2 a

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0 1 = 0 // axiom 3 a ii) If x = 1, then we have 1 1 = 1 // axiom 2 a

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0+0 = 0 // axiom 2 b ii) If x = 1, then we have 1+1 = 1 // axiom 1 b

The Boolean variable x can have only two possible values: 0 or 1. Let’s look at each case separately. i) If x = 0, then we have 0+0 = 0 // axiom 2 b ii) If x = 1, then we have 1+1 = 1 // axiom 1 b

i) If x = 0, then we have 0 0 = 0 ii) // axiom 1 a If x = 1, then we have 1 1 = 1 // axiom 2 a

i) If x = 0, then we have 0 0 = 0 ii) // axiom 1 a If x = 1, then we have 1 1 = 1 // axiom 2 a

i) If x = 0, then we have 0+0 = 0 ii) // axiom 2 b If x = 1, then we have 1+1 = 1 // axiom 1 b

i) If x = 0, then we have 0+0 = 0 ii) // axiom 2 b If x = 1, then we have 1+1 = 1 // axiom 1 b

i) If x = 0, then we have 0 1 = 0 ii) // axiom 3 a If x = 1, then we have 1 0 = 0 // axiom 3 a

i) If x = 0, then we have 0 1 = 0 ii) // axiom 3 a If x = 1, then we have 1 0 = 0 // axiom 3 a

i) If x = 0, then we have 0+1 = 1 ii) // axiom 3 b If x = 1, then we have 1+0 = 1 // axiom 3 b

i) If x = 0, then we have 0+1 = 1 ii) // axiom 3 b If x = 1, then we have 1+0 = 1 // axiom 3 b

i) If x = 0, then we have x = 1 // axiom 4 a let y = x = 1, then we have y=0 // axiom 4 b Therefore, x = x (when x =0)

ii) If x = 1, then we have x = 0 // axiom 4 b let y = x = 0, then we have y=1 // axiom 4 a Therefore, x = x (when x =1)

x y y x

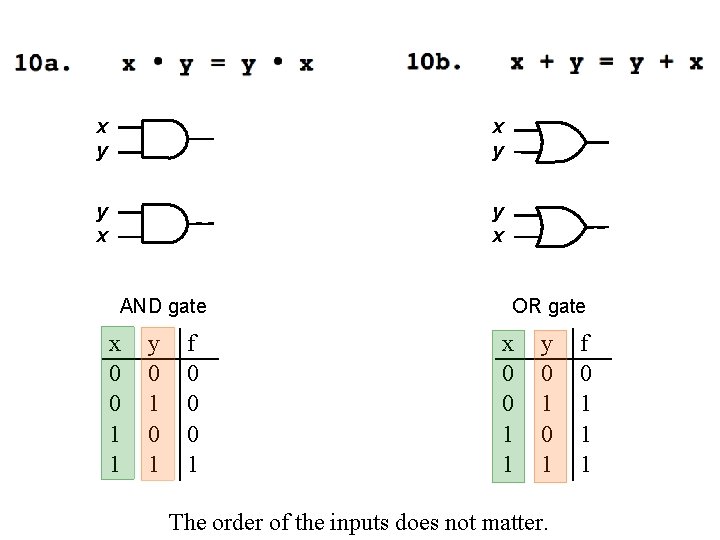
x y y x AND gate x 0 0 1 1 y 0 1 f 0 0 0 1 OR gate x 0 0 1 1 y 0 1 The order of the inputs does not matter. f 0 1 1 1

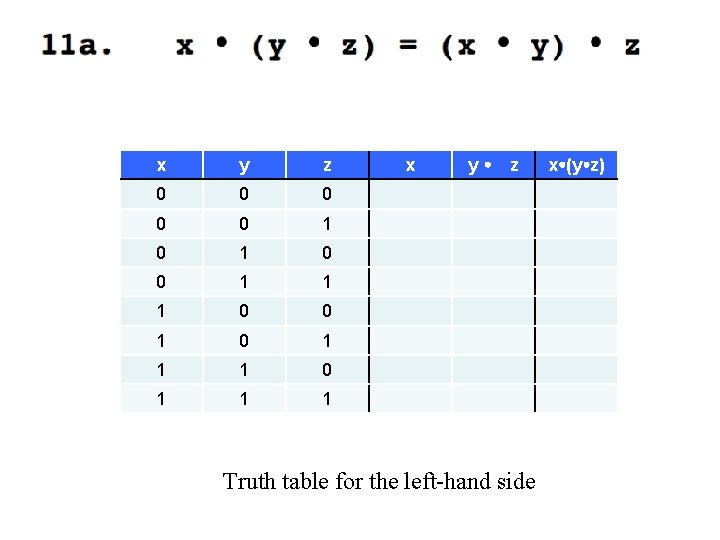
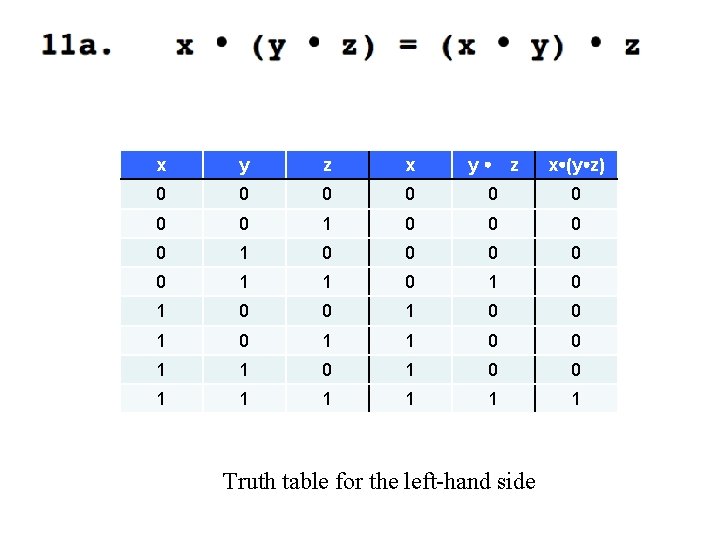
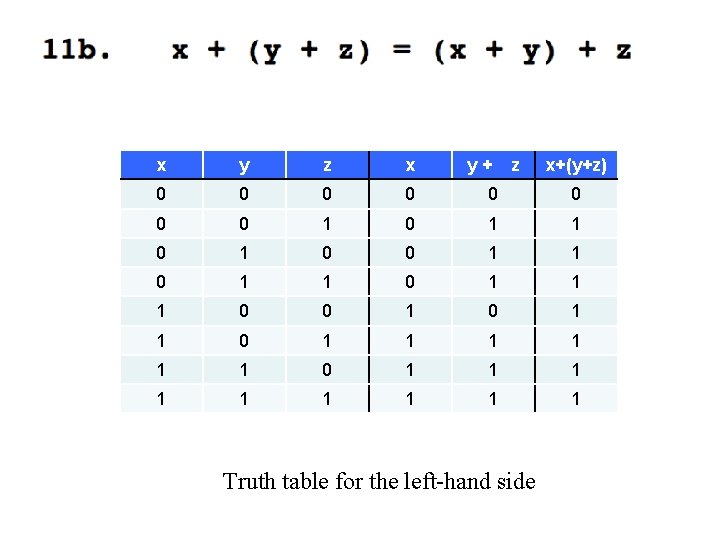
x y z 0 0 0 1 1 1 0 0 1 1 1 x y z Truth table for the left-hand side x (y z)

y x y z x 0 0 0 0 1 1 0 0 1 0 1 1 1 z Truth table for the left-hand side x (y z)

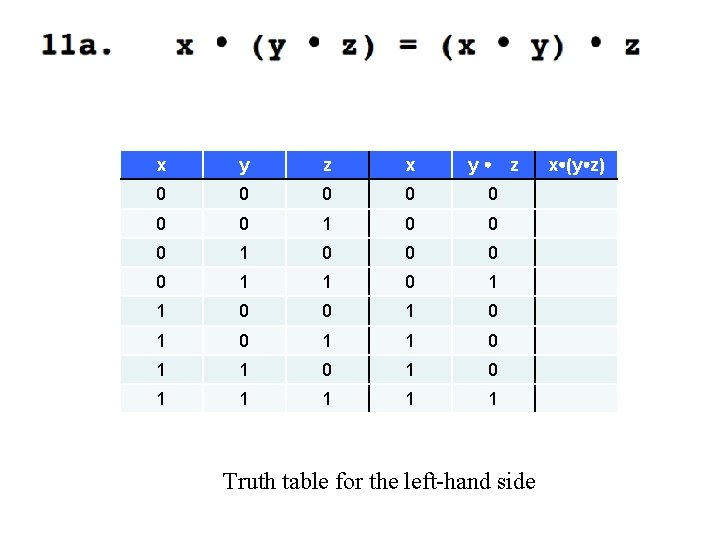
y z x (y z) x y z x 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 Truth table for the left-hand side

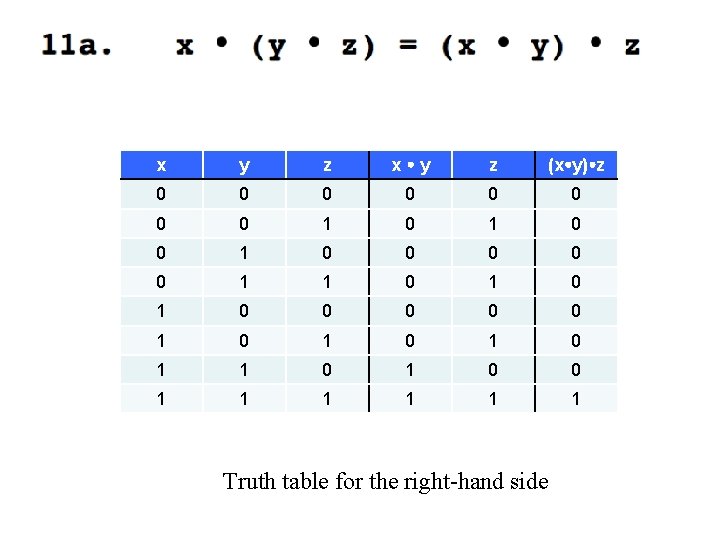
x y z (x y) z 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1 Truth table for the right-hand side

These two are identical, which concludes the proof.

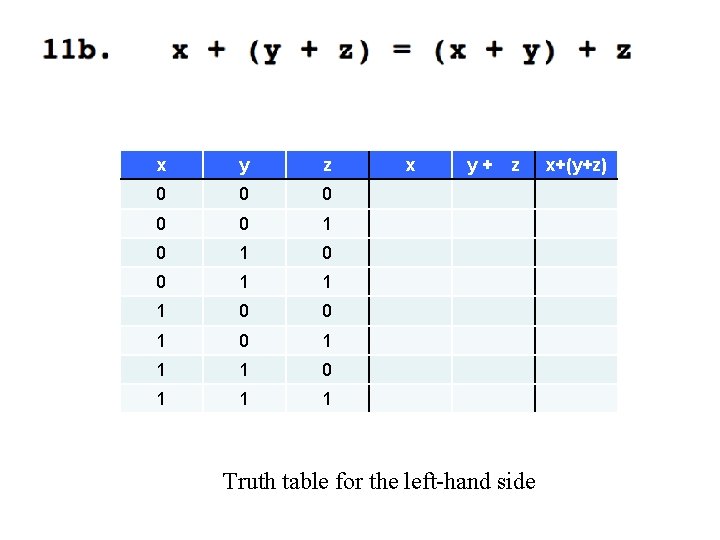
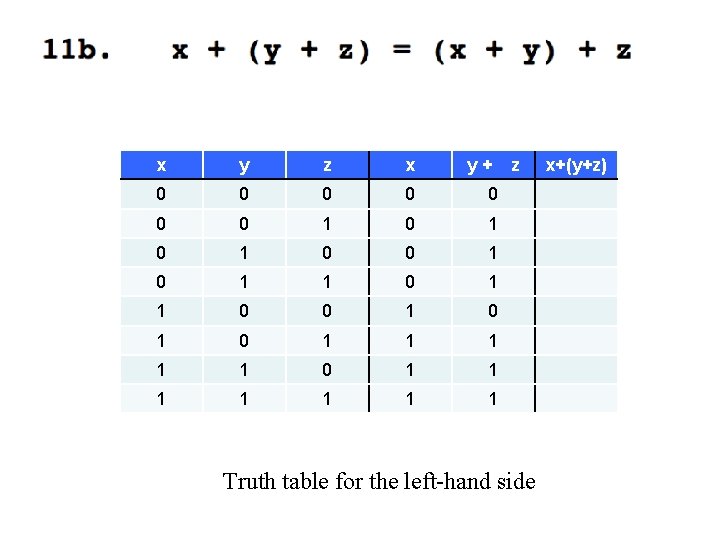
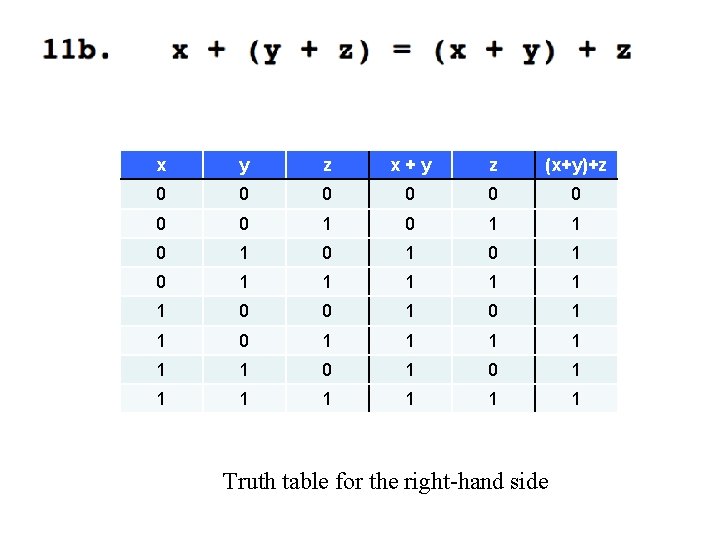
x y z 0 0 0 1 1 1 0 0 1 1 1 x y+ z Truth table for the left-hand side x+(y+z)

y+ x y z x 0 0 0 0 1 0 1 0 1 1 0 0 1 0 1 1 1 1 z Truth table for the left-hand side x+(y+z)

y+ z x y z x 0 0 0 0 1 0 1 0 0 1 1 0 1 1 1 1 1 1 1 Truth table for the left-hand side x+(y+z)

x y z x+y z (x+y)+z 0 0 0 0 1 0 1 1 1 0 0 1 1 1 0 1 1 1 1 Truth table for the right-hand side

These two are identical, which concludes the proof.

The Venn Diagram Representation x y z x y +z

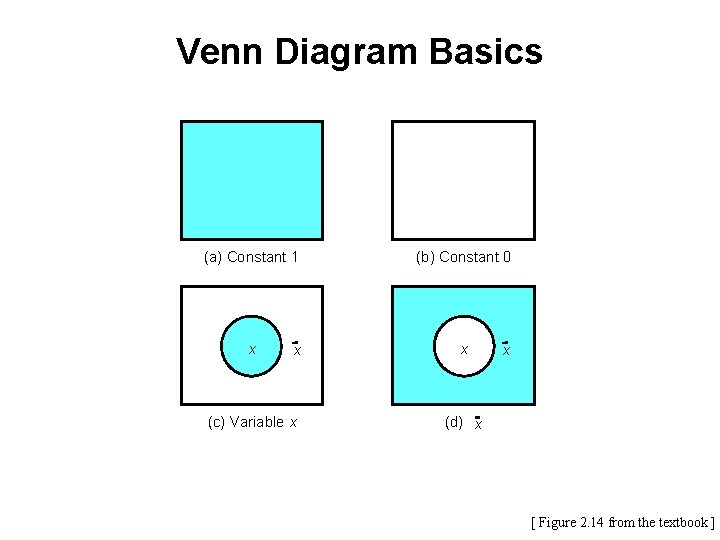
Venn Diagram Basics (a) Constant 1 (b) Constant 0 x x x (c) Variable x x (d) x [ Figure 2. 14 from the textbook ]

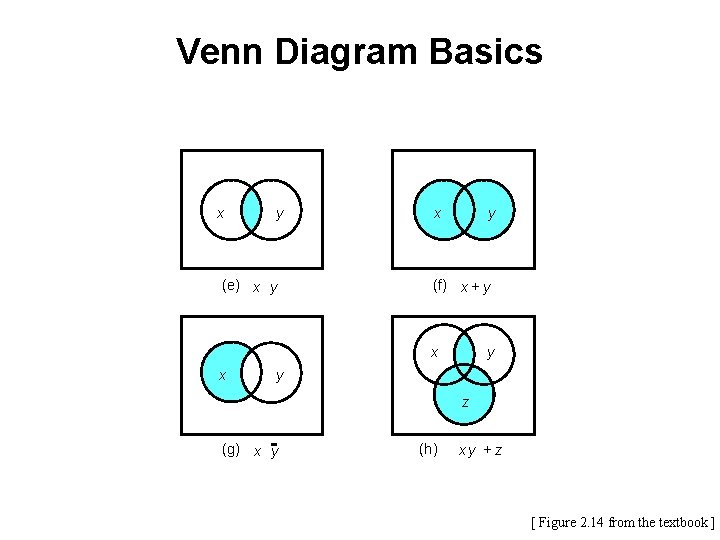
Venn Diagram Basics x y (e) x y (f) x + y x x y y z (g) x y (h) xy +z [ Figure 2. 14 from the textbook ]

Let’s Prove the Distributive Properties

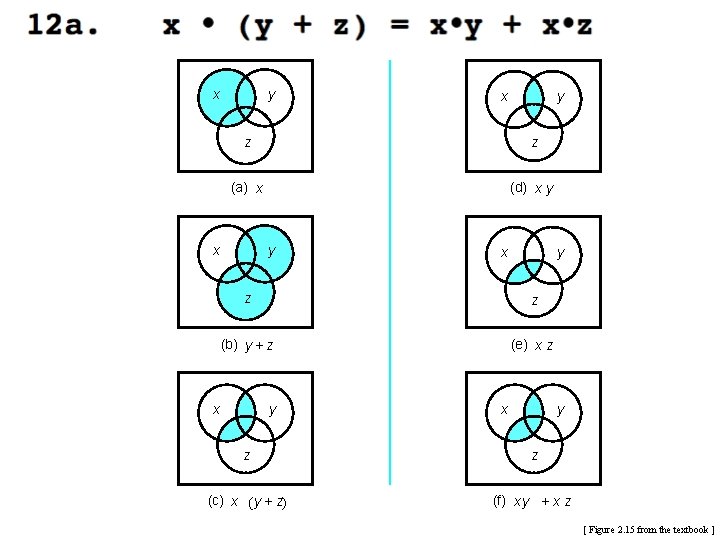
x y z z (a) x (d) x y x y z z (b) y + z (e) x z x y z z (c) x ( y + z) (f) x y + x z [ Figure 2. 15 from the textbook ]

[ Figure 2. 17 from the textbook ]

Try to prove these ones at home

De. Morgan’s Theorem

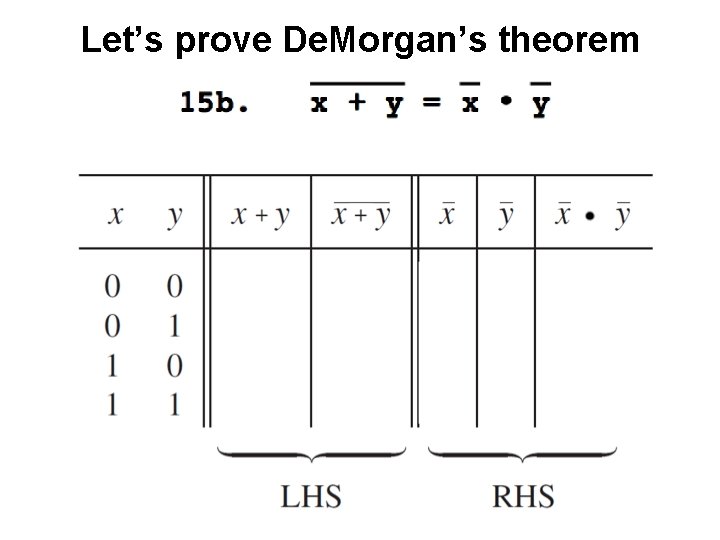
Proof of De. Morgan’s theorem [ Figure 2. 13 from the textbook ]

Alternative Proof of De. Morgan’s theorem [ Figure 2. 18 from the textbook ]

Let’s prove De. Morgan’s theorem

Try to prove these ones at home

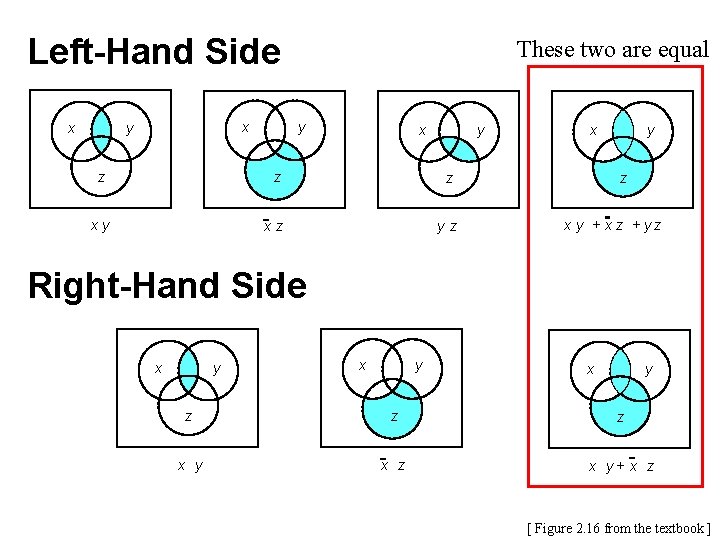
Venn Diagram Example Proof of Property 17 a

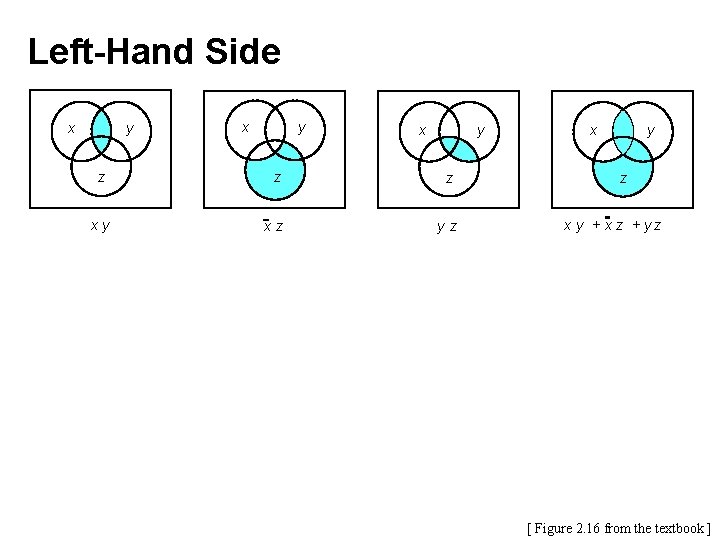
Left-Hand Side x y x y z z z xy xz yz x y + x z + yz [ Figure 2. 16 from the textbook ]

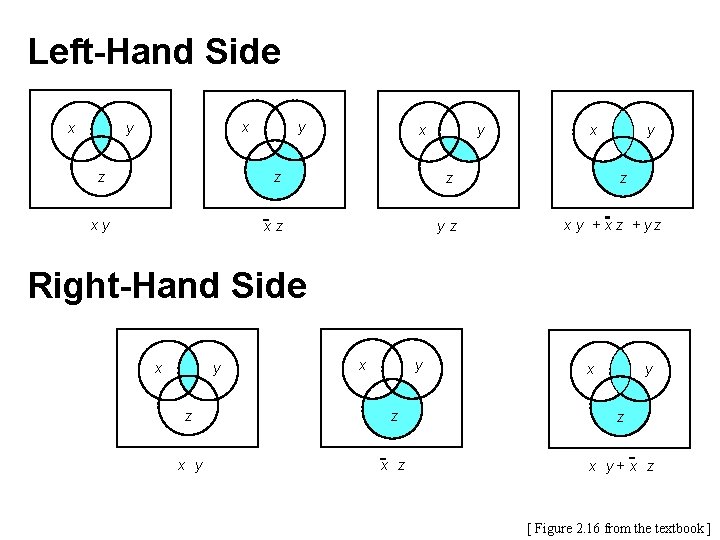
Left-Hand Side x x y y x y z z z xy xz yz x y + x z + yz Right-Hand Side x y x y z z z x y x z x y+ x z [ Figure 2. 16 from the textbook ]

Left-Hand Side x x y These two are equal y x y z z z xy xz yz x y + x z + yz Right-Hand Side x y x y z z z x y x z x y+ x z [ Figure 2. 16 from the textbook ]

Questions?

THE END