Cpr E 281 Digital Logic Instructor Alexander Stoytchev






![Building an AND gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic] Building an AND gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-18.jpg)
![Building an OR gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic] Building an OR gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-19.jpg)




![Minterms and Maxterms (with three variables) [ Figure 2. 22 from the textbook ] Minterms and Maxterms (with three variables) [ Figure 2. 22 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-24.jpg)


![Let’s Derive the POS form [ Figure 2. 31 from the textbook ] Let’s Derive the POS form [ Figure 2. 31 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-28.jpg)






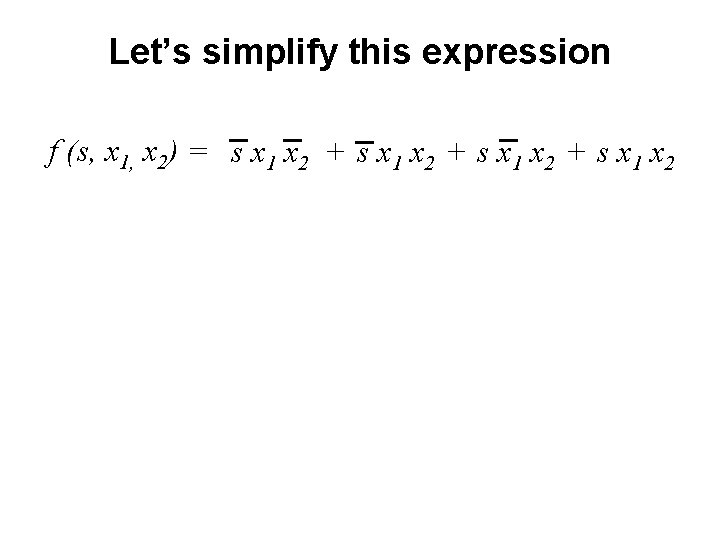
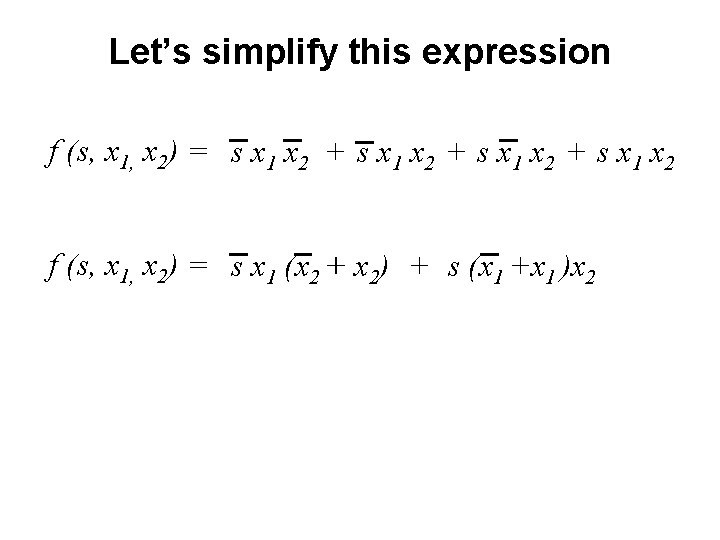
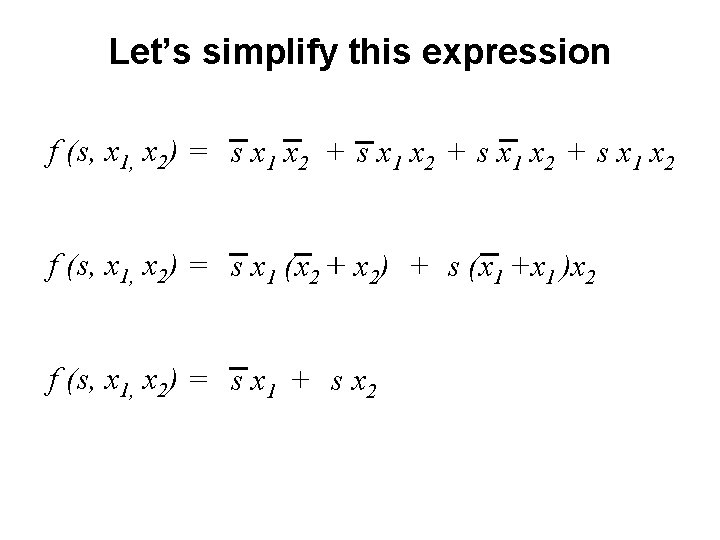


![Graphical Symbol and Truth Table [ Figure 4. 2 a-b from the textbook ] Graphical Symbol and Truth Table [ Figure 4. 2 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-47.jpg)

![The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer] The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-49.jpg)
![The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer] The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-50.jpg)
![The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer] The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-51.jpg)
![The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer] The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-52.jpg)
![4 -1 Multiplexer (SOP circuit) [ Figure 4. 2 c from the textbook ] 4 -1 Multiplexer (SOP circuit) [ Figure 4. 2 c from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-53.jpg)
![Display of numbers [ Figure 2. 34 from the textbook ] Display of numbers [ Figure 2. 34 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-61.jpg)


- Slides: 65

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Design Examples Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • HW 3 is out • It is due on Monday Feb 3 @ 4 pm. • Please write clearly on the first page (in BLOCK CAPITAL letters) the following three things: § Your First and Last Name § Your Student ID Number § Your Lab Section Letter • Also, please § Staple your pages § Use Letter-sized sheets

Administrative Stuff • TA Office Hours: • David Johnston Thursdays @ 10 -12 am Location: TLA (Coover Hall - first floor) • Pratik Mishra Thursdays @ 2 -4 pm Location: Durham Hall, room 309.

Administrative Stuff • Homework Submission Guidelines • Please follow the guidelines that were e-mailed to you. • Let me know if you did not get that email.

Quick Review

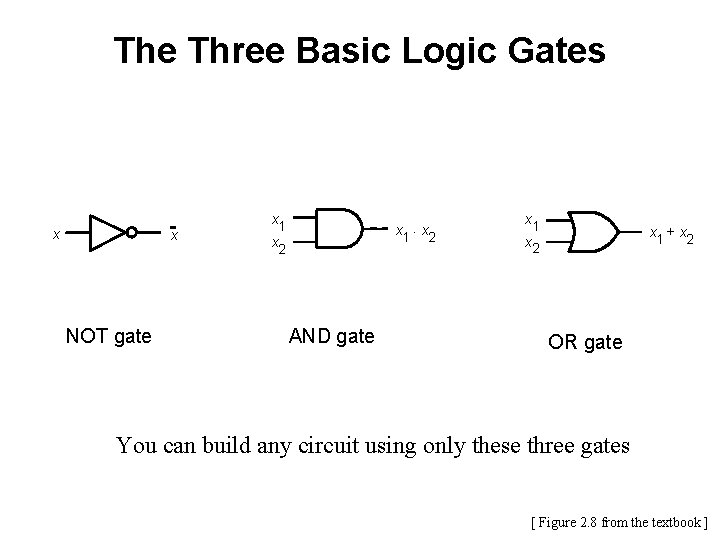
The Three Basic Logic Gates x x NOT gate x 1 x 2 x 1 × x 2 AND gate x 1 x 2 x 1 + x 2 OR gate You can build any circuit using only these three gates [ Figure 2. 8 from the textbook ]

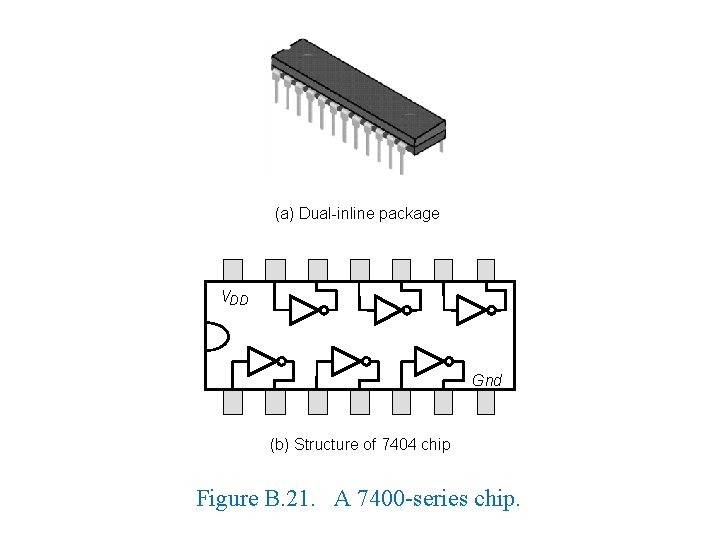
(a) Dual-inline package VDD Gnd (b) Structure of 7404 chip Figure B. 21. A 7400 -series chip.

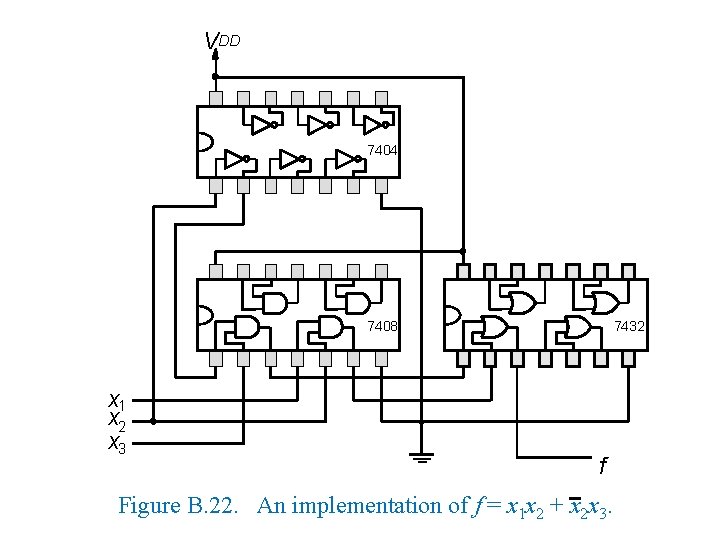
VDD 7404 7408 x 1 x 2 x 3 7432 f Figure B. 22. An implementation of f = x 1 x 2 + x 2 x 3.

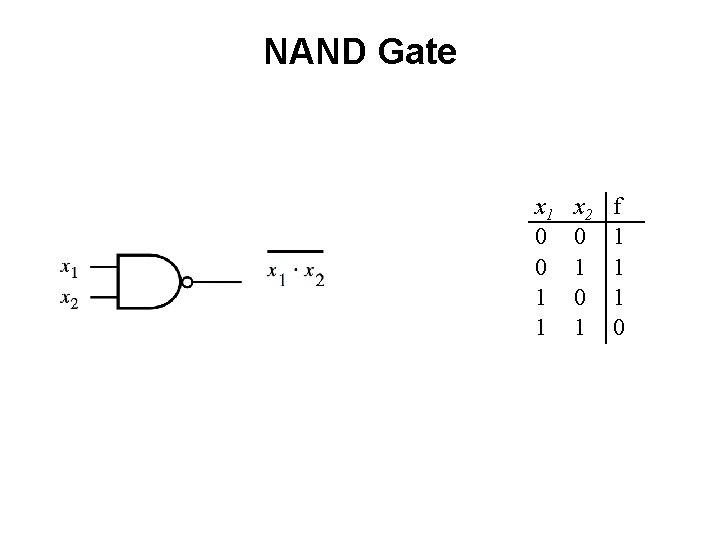
NAND Gate x 1 0 0 1 1 x 2 0 1 f 1 1 1 0

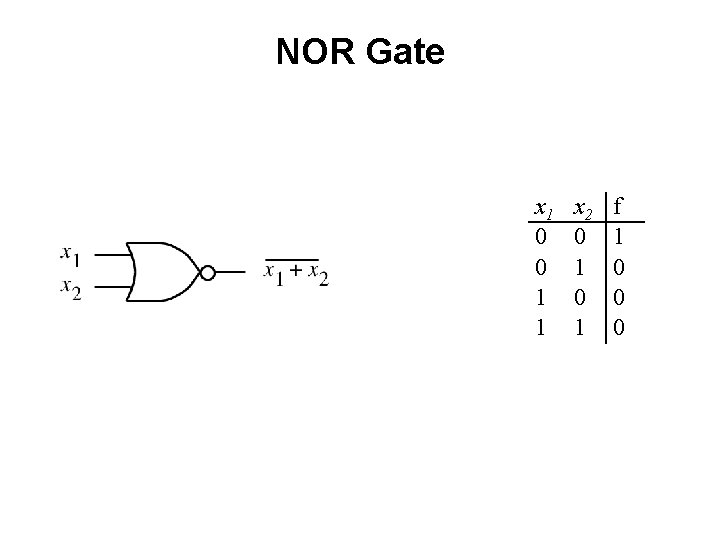
NOR Gate x 1 0 0 1 1 x 2 0 1 f 1 0 0 0

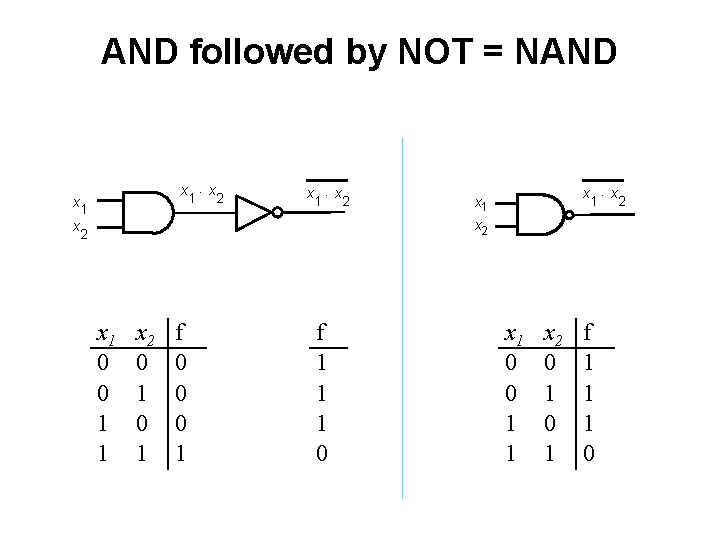
AND followed by NOT = NAND x x x ×x 1 2 1 x ×x 1 2 x 1 x 2 2 x 1 0 0 1 1 x 2 0 1 f 0 0 0 1 f 1 1 1 0 x 1 0 0 1 1 x 2 0 1 f 1 1 1 0

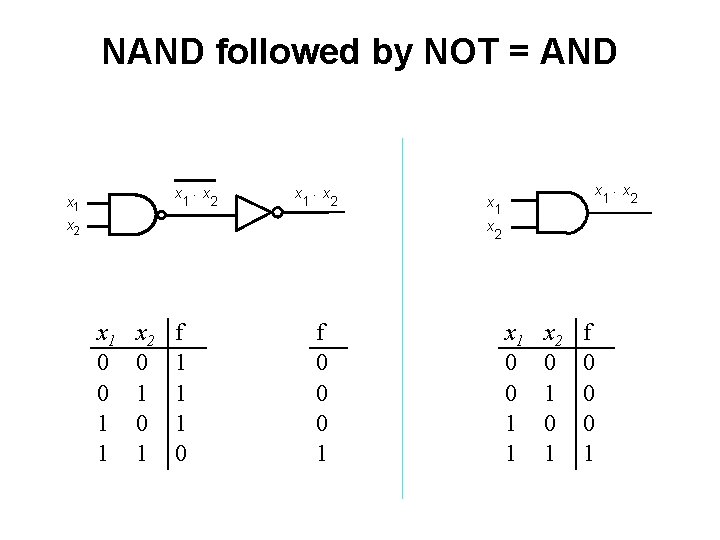
NAND followed by NOT = AND x ×x 1 2 x 1 x ×x 1 2 x x x 1 0 0 1 1 x 2 0 1 f 1 1 1 0 f 0 0 0 1 x ×x 1 2 x 1 0 0 1 1 x 2 0 1 f 0 0 0 1

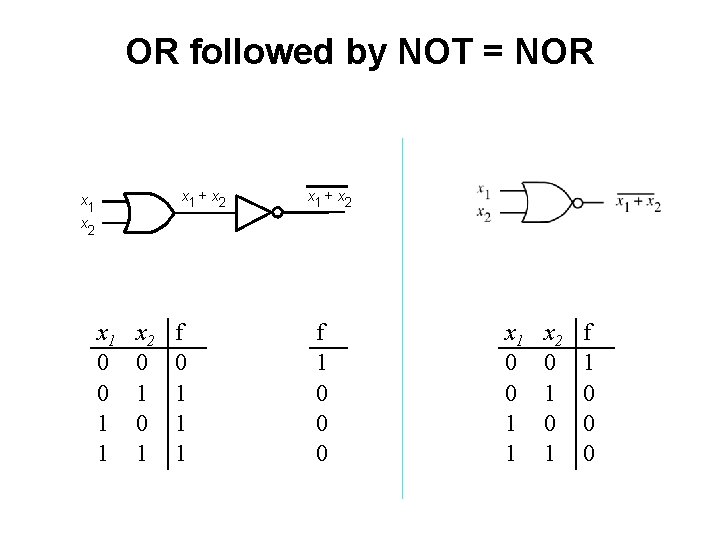
OR followed by NOT = NOR x 1 + x 2 x 1 0 0 1 1 x 2 0 1 f 0 1 1 1 x 1 + x 2 f 1 0 0 0 x 1 0 0 1 1 x 2 0 1 f 1 0 0 0

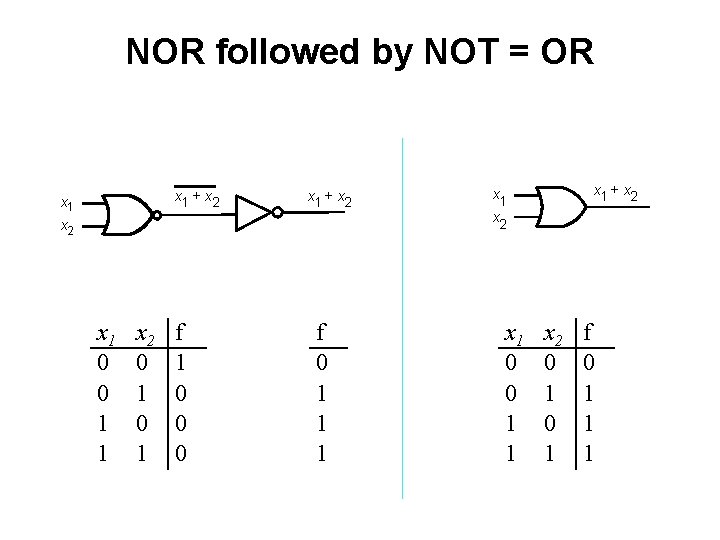
NOR followed by NOT = OR x 1 + x 2 x 1 0 0 1 1 x 2 0 1 f 1 0 0 0 f 0 1 1 1 x 1 + x 2 x 1 0 0 1 1 x 2 0 1 f 0 1 1 1

Why do we need two more gates? They can be implemented with fewer transistors. (more about this later)

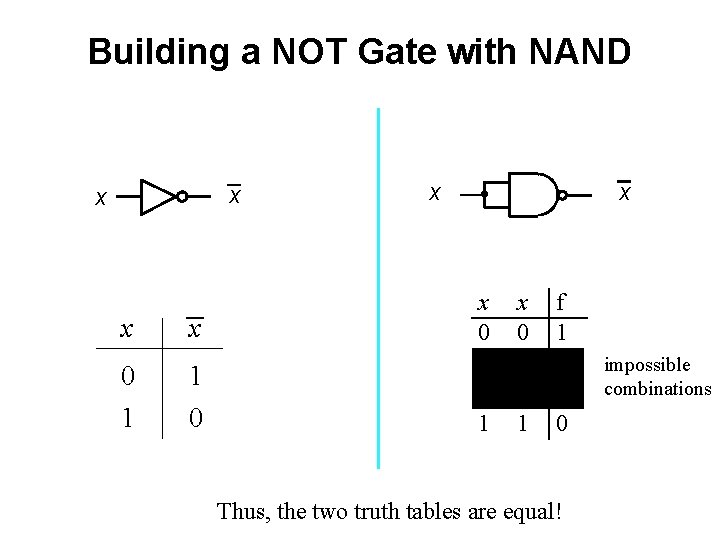
Building a NOT Gate with NAND x x x 0 1 x 1 0 x x x 0 0 1 1 x 0 1 f 1 1 1 0 Thus, the two truth tables are equal! impossible combinations
![Building an AND gate with NAND gates http en wikipedia orgwikiNANDlogic Building an AND gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-18.jpg)
Building an AND gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]
![Building an OR gate with NAND gates http en wikipedia orgwikiNANDlogic Building an OR gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-19.jpg)
Building an OR gate with NAND gates [http: //en. wikipedia. org/wiki/NAND_logic]

Implications Any Boolean function can be implemented with only NAND gates!

Implications Any Boolean function can be implemented with only NAND gates! The same is also true for NOR gates!

Another Synthesis Example

Truth table for a three-way light control [ Figure 2. 31 from the textbook ]
![Minterms and Maxterms with three variables Figure 2 22 from the textbook Minterms and Maxterms (with three variables) [ Figure 2. 22 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-24.jpg)
Minterms and Maxterms (with three variables) [ Figure 2. 22 from the textbook ]

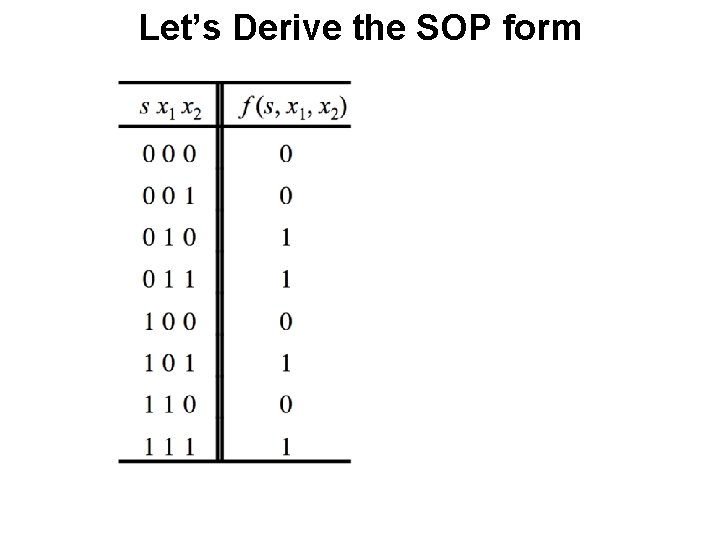
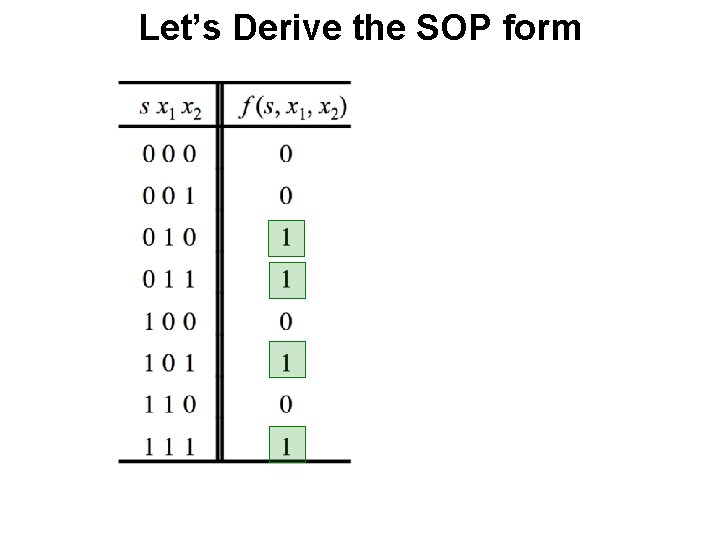
Let’s Derive the SOP form

Let’s Derive the SOP form

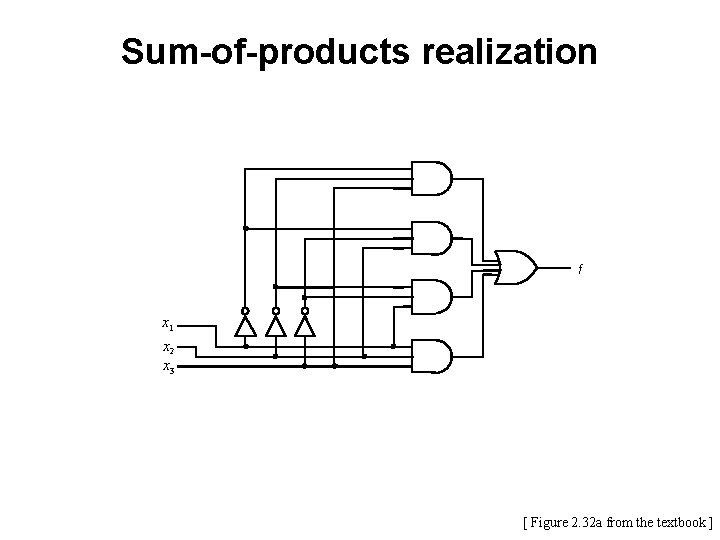
Sum-of-products realization f x 1 x 2 x 3 [ Figure 2. 32 a from the textbook ]
![Lets Derive the POS form Figure 2 31 from the textbook Let’s Derive the POS form [ Figure 2. 31 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-28.jpg)
Let’s Derive the POS form [ Figure 2. 31 from the textbook ]

Let’s Derive the POS form

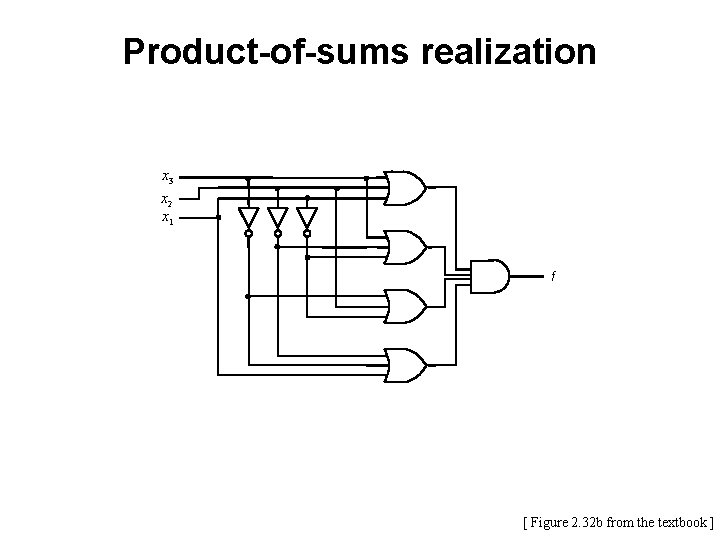
Product-of-sums realization x 3 x 2 x 1 f [ Figure 2. 32 b from the textbook ]

Multiplexers

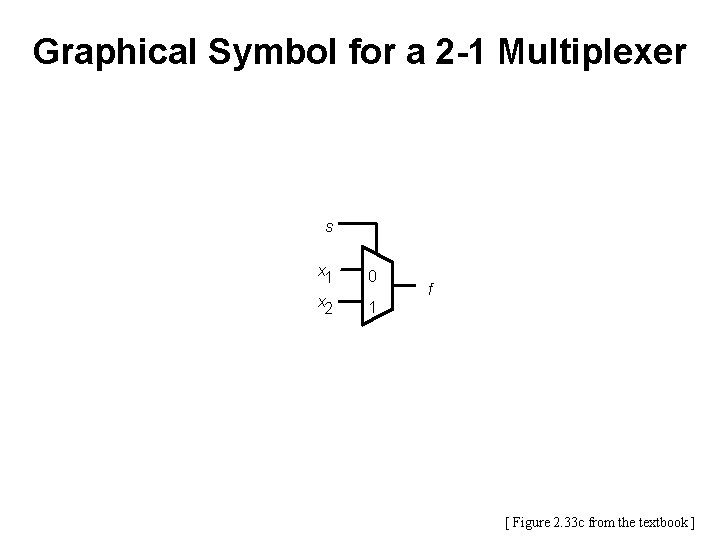
2 -1 Multiplexer (Definition) • Has two inputs: x 1 and x 2 • Also has another input line s • If s=0, then the output is equal to x 1 • If s=1, then the output is equal to x 2

Graphical Symbol for a 2 -1 Multiplexer s x 1 0 x 2 1 f [ Figure 2. 33 c from the textbook ]

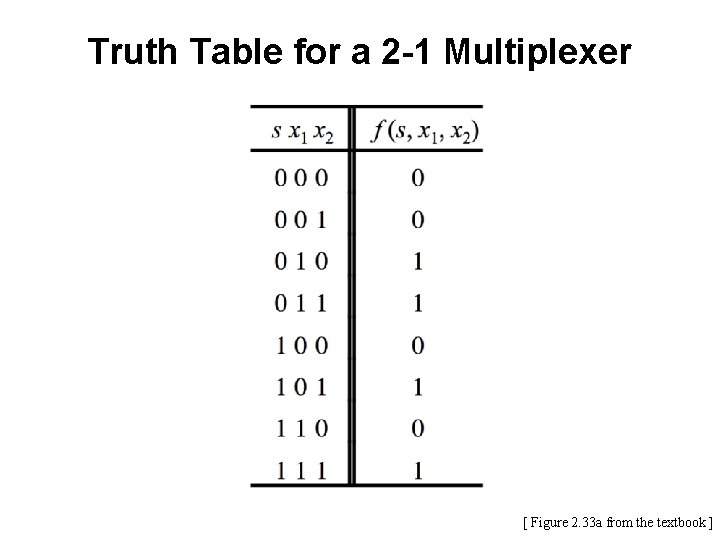
Truth Table for a 2 -1 Multiplexer [ Figure 2. 33 a from the textbook ]

Let’s Derive the SOP form

Let’s Derive the SOP form

Let’s Derive the SOP form Where should we put the negation signs? s x 1 x 2

Let’s Derive the SOP form s x 1 x 2

Let’s Derive the SOP form s x 1 x 2 f (s, x 1, x 2) = s x 1 x 2 + s x 1 x 2
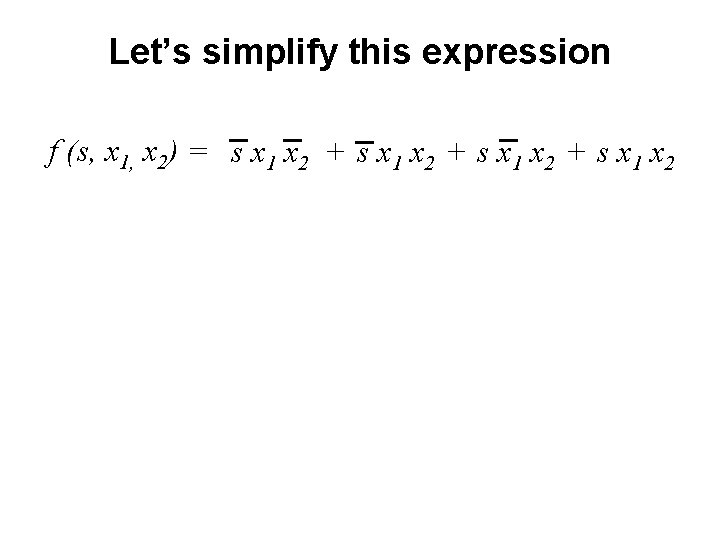
Let’s simplify this expression f (s, x 1, x 2) = s x 1 x 2 + s x 1 x 2
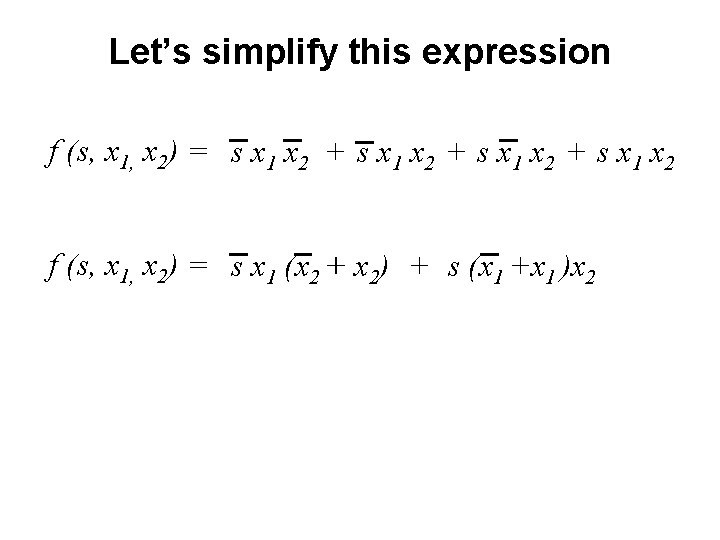
Let’s simplify this expression f (s, x 1, x 2) = s x 1 x 2 + s x 1 x 2 f (s, x 1, x 2) = s x 1 (x 2 + x 2) + s (x 1 +x 1 )x 2
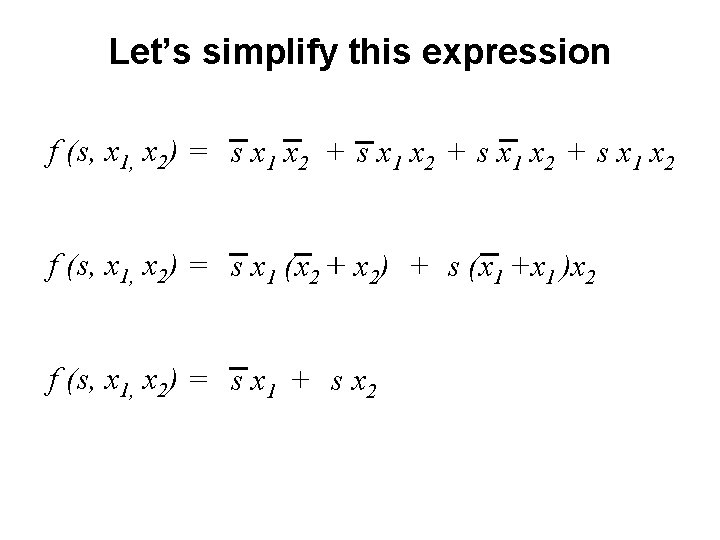
Let’s simplify this expression f (s, x 1, x 2) = s x 1 x 2 + s x 1 x 2 f (s, x 1, x 2) = s x 1 (x 2 + x 2) + s (x 1 +x 1 )x 2 f (s, x 1, x 2) = s x 1 + s x 2

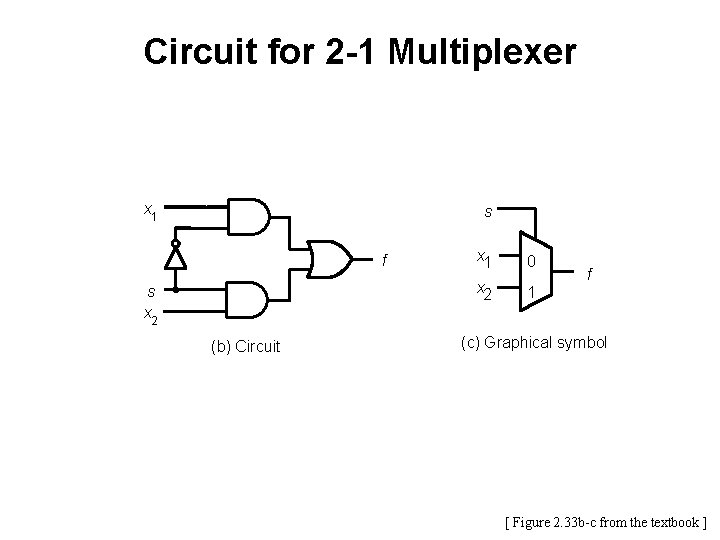
Circuit for 2 -1 Multiplexer x 1 s f s x 2 (b) Circuit x 1 0 x 2 1 f (c) Graphical symbol [ Figure 2. 33 b-c from the textbook ]

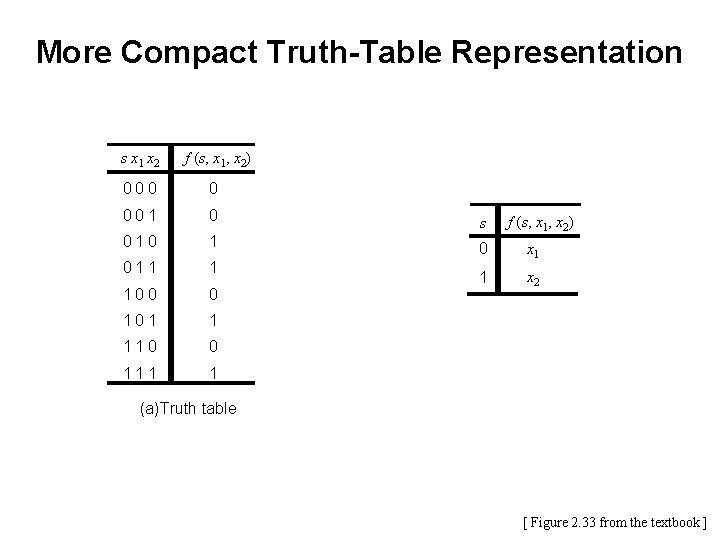
More Compact Truth-Table Representation s x 1 x 2 f (s, x 1, x 2) 000 0 001 0 s 010 1 0 011 1 x 1 100 0 1 x 2 101 1 110 0 111 1 f (s, x 1, x 2) (a)Truth table [ Figure 2. 33 from the textbook ]

4 -1 Multiplexer (Definition) • Has four inputs: w 0 , w 1, w 2, w 3 • Also has two select lines: s 1 and s 0 • • If s 1=0 and s 0=0, then the output f is equal to w 0 If s 1=0 and s 0=1, then the output f is equal to w 1 If s 1=1 and s 0=0, then the output f is equal to w 2 If s 1=1 and s 0=1, then the output f is equal to w 3

4 -1 Multiplexer (Definition) • Has four inputs: w 0 , w 1, w 2, w 3 • Also has two select lines: s 1 and s 0 • • If s 1=0 and s 0=0, then the output f is equal to w 0 If s 1=0 and s 0=1, then the output f is equal to w 1 If s 1=1 and s 0=0, then the output f is equal to w 2 If s 1=1 and s 0=1, then the output f is equal to w 3 We’ll talk more about this when we get to chapter 4, but here is a quick preview.
![Graphical Symbol and Truth Table Figure 4 2 ab from the textbook Graphical Symbol and Truth Table [ Figure 4. 2 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-47.jpg)
Graphical Symbol and Truth Table [ Figure 4. 2 a-b from the textbook ]

The long-form truth table
![The longform truth table http www absoluteastronomy comtopicsMultiplexer The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-49.jpg)
The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]
![The longform truth table http www absoluteastronomy comtopicsMultiplexer The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-50.jpg)
The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]
![The longform truth table http www absoluteastronomy comtopicsMultiplexer The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-51.jpg)
The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]
![The longform truth table http www absoluteastronomy comtopicsMultiplexer The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-52.jpg)
The long-form truth table [http: //www. absoluteastronomy. com/topics/Multiplexer]
![4 1 Multiplexer SOP circuit Figure 4 2 c from the textbook 4 -1 Multiplexer (SOP circuit) [ Figure 4. 2 c from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-53.jpg)
4 -1 Multiplexer (SOP circuit) [ Figure 4. 2 c from the textbook ]

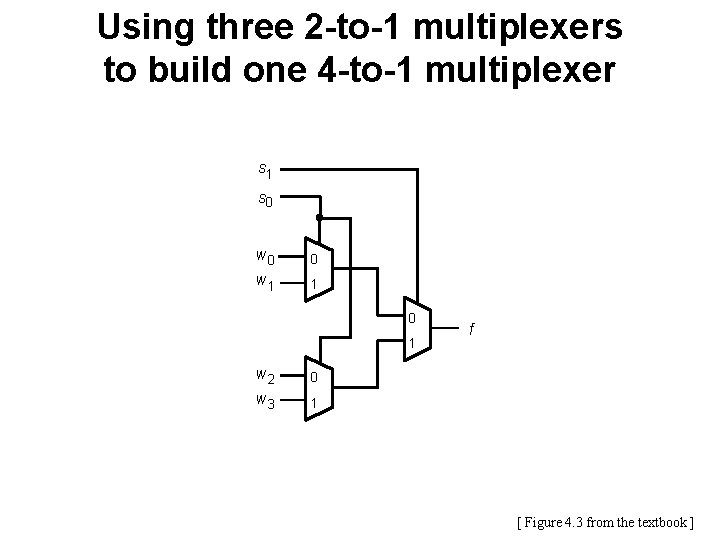
Using three 2 -to-1 multiplexers to build one 4 -to-1 multiplexer s 1 s 0 w 0 0 w 1 1 0 1 w 2 0 w 3 1 f [ Figure 4. 3 from the textbook ]

Using three 2 -to-1 multiplexers to build one 4 -to-1 multiplexer

Using three 2 -to-1 multiplexers to build one 4 -to-1 multiplexer

Using three 2 -to-1 multiplexers to build one 4 -to-1 multiplexer

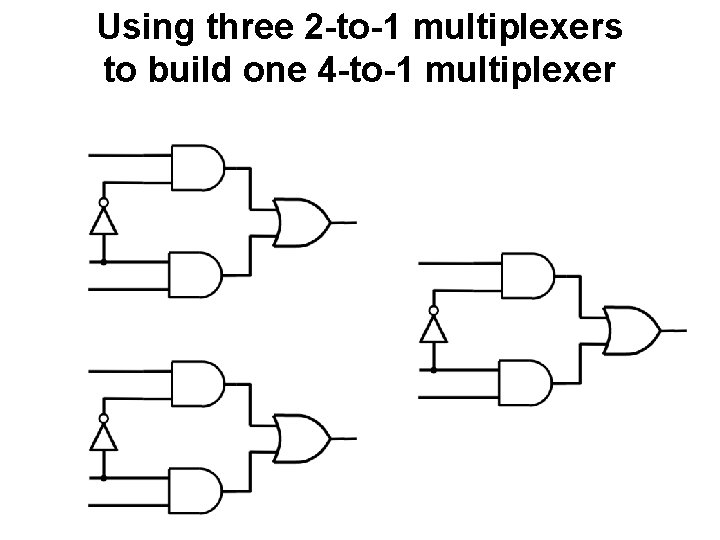
Using three 2 -to-1 multiplexers to build one 4 -to-1 multiplexer w 0 s 1 s 0 w 1 f w 2 w 3

That is different from the SOP form of the 4 -1 multiplexer shown below, which uses less gates

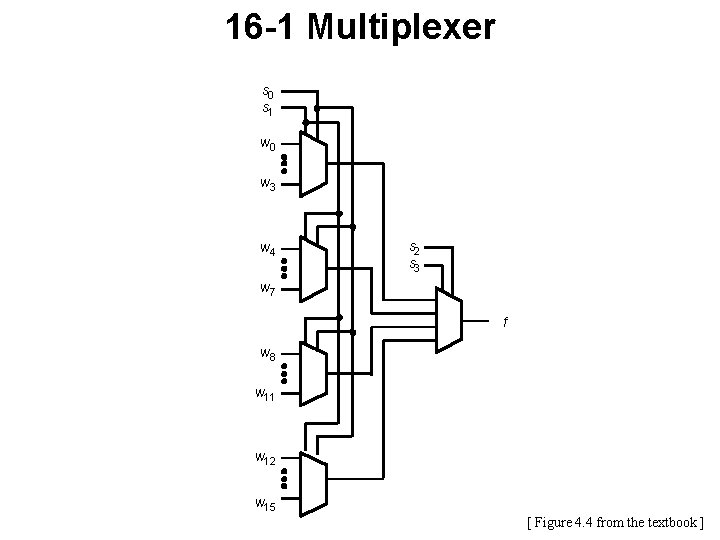
16 -1 Multiplexer s 0 s 1 w 0 w 3 w 4 s 2 s 3 w 7 f w 8 w 11 w 12 w 15 [ Figure 4. 4 from the textbook ]
![Display of numbers Figure 2 34 from the textbook Display of numbers [ Figure 2. 34 from the textbook ]](https://slidetodoc.com/presentation_image_h/98fa1f362a5b1e25f4ea94c69bcc59d7/image-61.jpg)
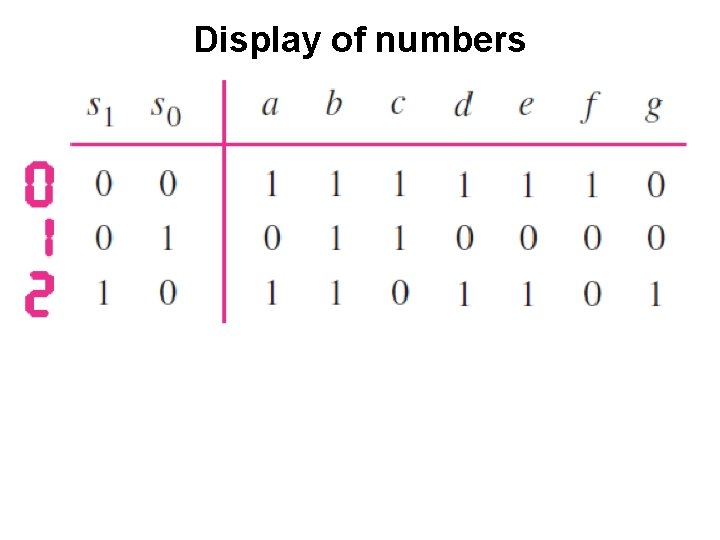
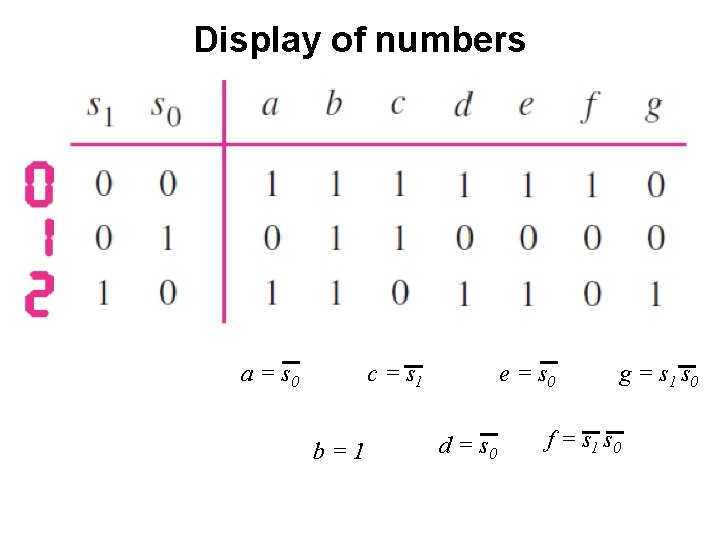
Display of numbers [ Figure 2. 34 from the textbook ]

Display of numbers

Display of numbers a = s 0 c = s 1 b=1 e = s 0 d = s 0 g = s 1 s 0 f = s 1 s 0

Questions?

THE END