Cpr E 281 Digital Logic Instructor Alexander Stoytchev

  • Slides: 84
Download presentation
Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Serial Adder Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright ©

Serial Adder Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • Homework 10 is out • It is due on Monday Nov

Administrative Stuff • Homework 10 is out • It is due on Monday Nov 17, 2014

Quick Review

Quick Review

Adding two bits (there are four possible cases) [ Figure 3. 1 a from

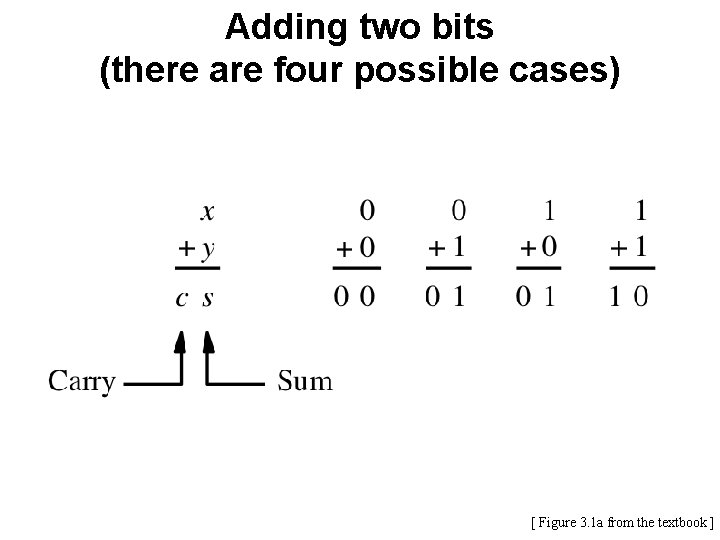
Adding two bits (there are four possible cases) [ Figure 3. 1 a from the textbook ]

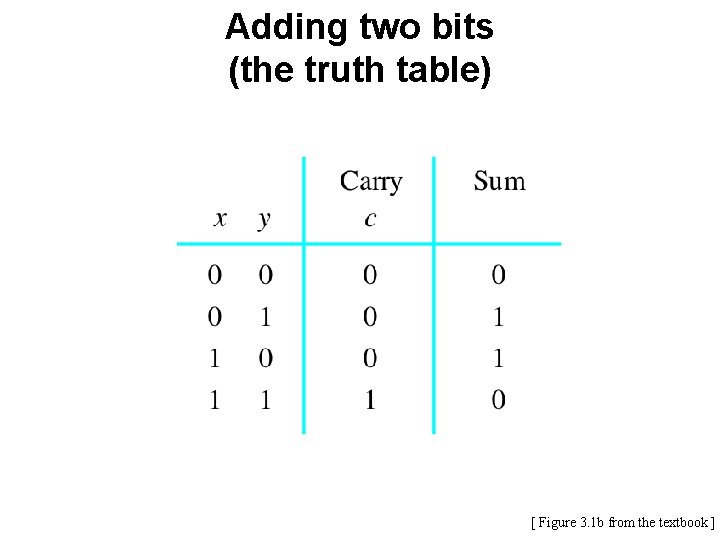
Adding two bits (the truth table) [ Figure 3. 1 b from the textbook

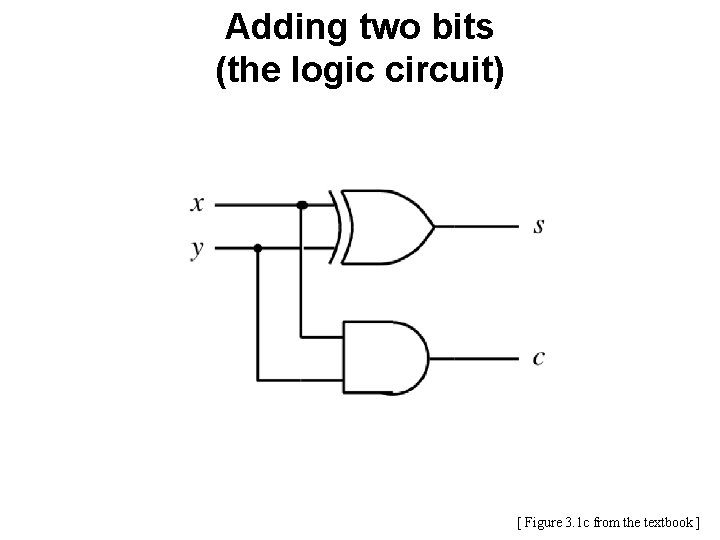
Adding two bits (the truth table) [ Figure 3. 1 b from the textbook ]

Adding two bits (the logic circuit) [ Figure 3. 1 c from the textbook

Adding two bits (the logic circuit) [ Figure 3. 1 c from the textbook ]

The Half-Adder [ Figure 3. 1 c-d from the textbook ]

The Half-Adder [ Figure 3. 1 c-d from the textbook ]

Addition of multibit numbers Bit position i [ Figure 3. 2 from the textbook

Addition of multibit numbers Bit position i [ Figure 3. 2 from the textbook ]

Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ]

Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ] [ Figure 3. 3 a from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

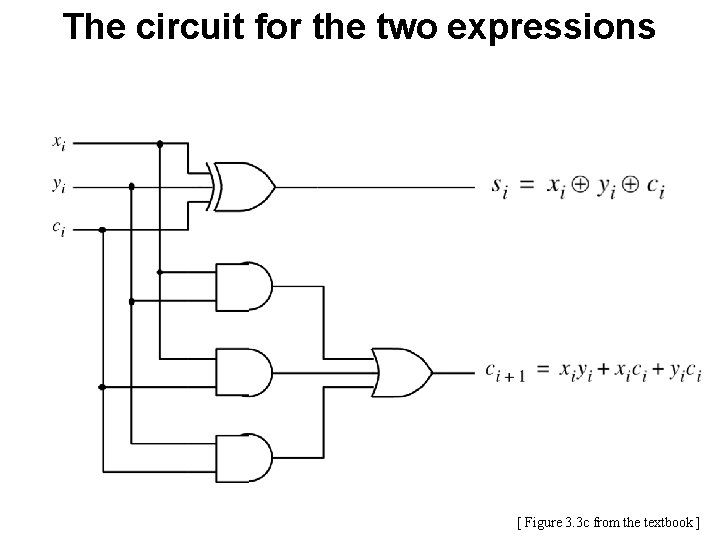
The circuit for the two expressions [ Figure 3. 3 c from the textbook

The circuit for the two expressions [ Figure 3. 3 c from the textbook ]

This is called the Full-Adder [ Figure 3. 3 c from the textbook ]

This is called the Full-Adder [ Figure 3. 3 c from the textbook ]

XOR Magic

XOR Magic

XOR Magic

XOR Magic

XOR Magic Can you prove this?

XOR Magic Can you prove this?

XOR Magic (si can be implemented in two different ways)

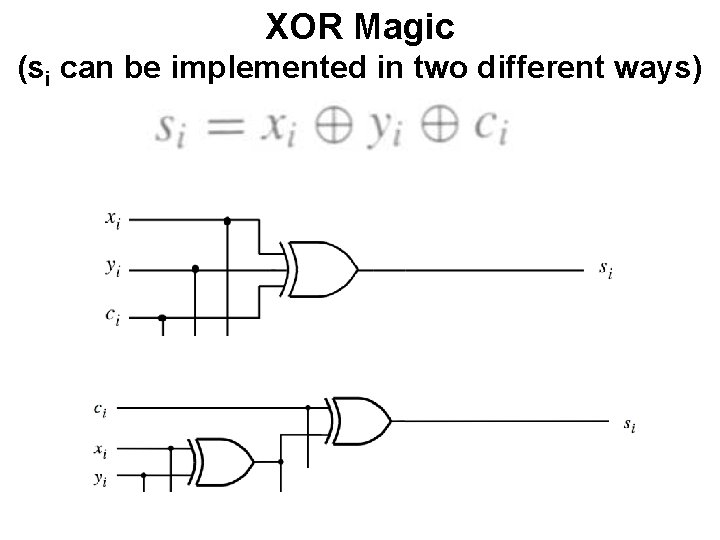
XOR Magic (si can be implemented in two different ways)

A decomposed implementation of the full-adder circuit s ci xi yi s HA HA

A decomposed implementation of the full-adder circuit s ci xi yi s HA HA c si ci + 1 c (a) Block diagram ci si xi yi ci + 1 (b) Detailed diagram [ Figure 3. 4 from the textbook ]

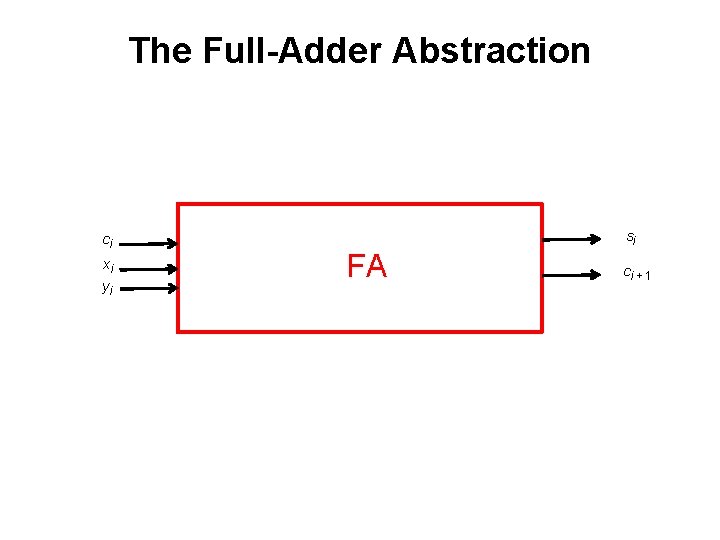
The Full-Adder Abstraction s ci xi yi s HA c si ci + 1

The Full-Adder Abstraction s ci xi yi s HA c si ci + 1

The Full-Adder Abstraction ci xi yi si FA ci + 1

The Full-Adder Abstraction ci xi yi si FA ci + 1

We can place the arrows anywhere xi ci+1 yi FA si ci

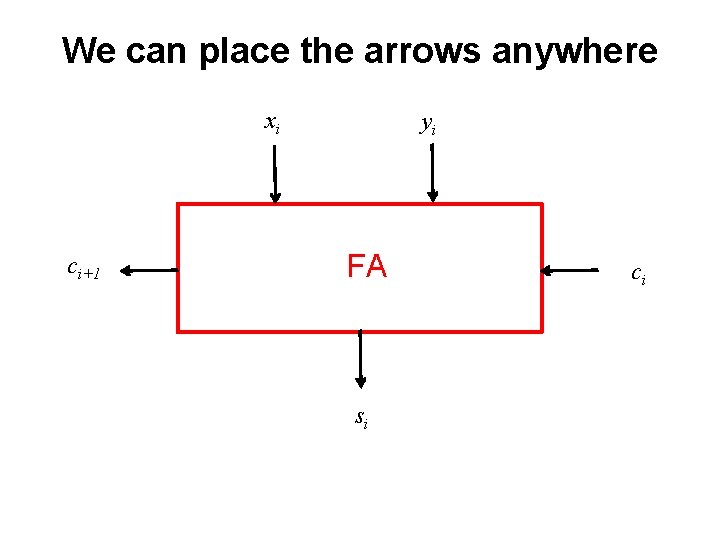
We can place the arrows anywhere xi ci+1 yi FA si ci

n-bit ripple-carry adder xn – 1 cn x 1 yn – 1 FA sn

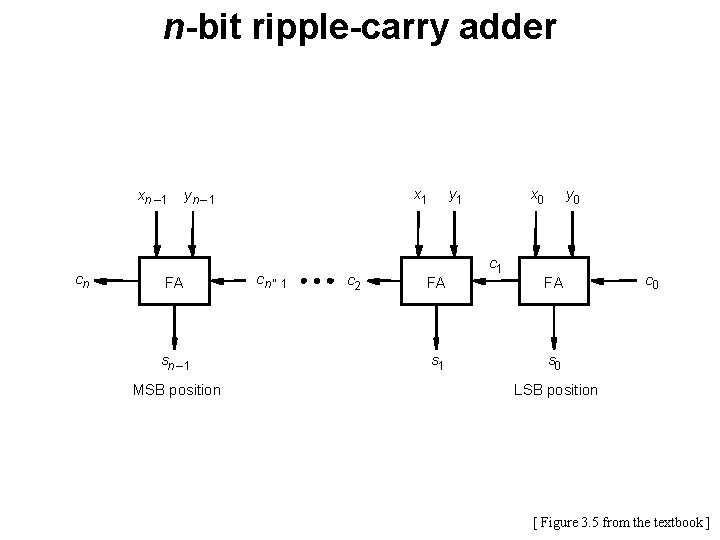
n-bit ripple-carry adder xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn ” 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA c 0 s 0 LSB position [ Figure 3. 5 from the textbook ]

n-bit ripple-carry adder abstraction xn – 1 cn x 1 yn – 1 FA

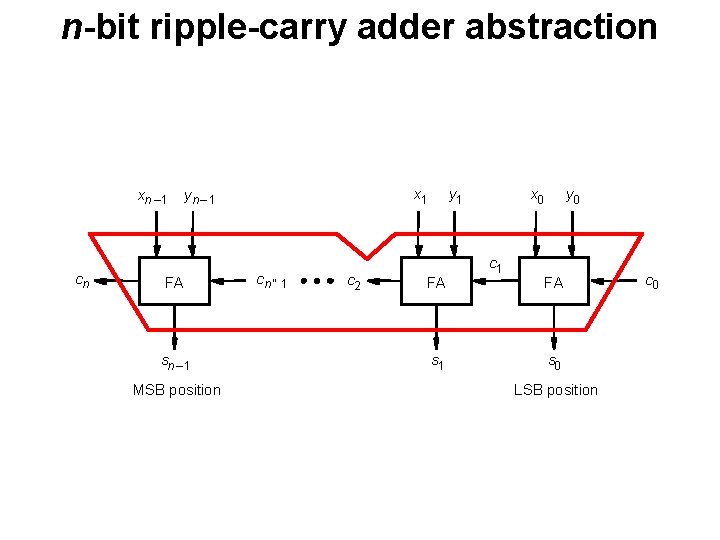
n-bit ripple-carry adder abstraction xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn ” 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA s 0 LSB position c 0

n-bit ripple-carry adder abstraction xn – 1 yn – 1 x 1 y 1

n-bit ripple-carry adder abstraction xn – 1 yn – 1 x 1 y 1 x 0 y 0 cn c 0 sn – 1 s 0

The x and y lines are typically grouped together for better visualization, but the

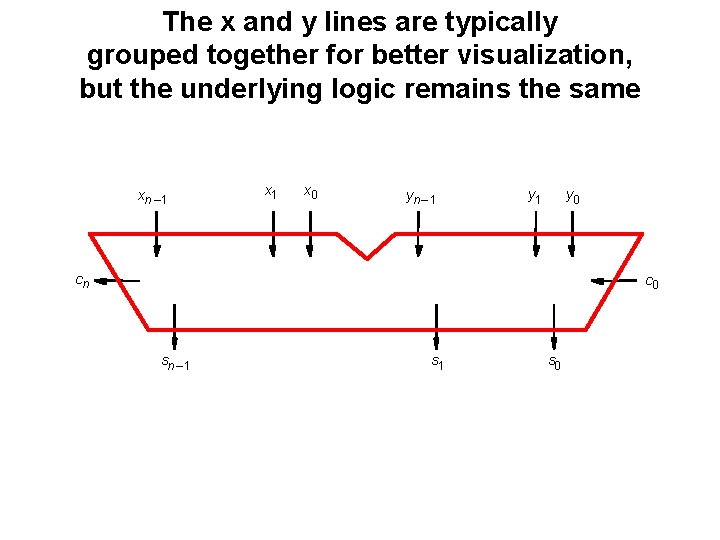
The x and y lines are typically grouped together for better visualization, but the underlying logic remains the same xn – 1 x 0 yn – 1 y 0 cn c 0 sn – 1 s 0

Serial Adder • The n-bit adder requires all bits to be provided at the

Serial Adder • The n-bit adder requires all bits to be provided at the same time. • In some cases we may want to add the numbers as the bits come in. • Also, with an n-bit adder we are limited to n-bits. Circuits for larger n are more complex. • Can we add arbitrarily long numbers.

Block diagram for the serial adder A a Shift register Adder FSM Shift register

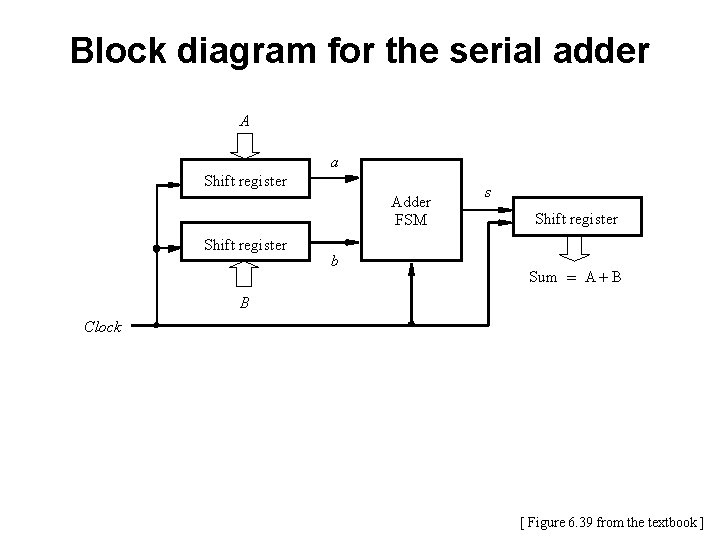
Block diagram for the serial adder A a Shift register Adder FSM Shift register b s Shift register Sum = A + B B Clock [ Figure 6. 39 from the textbook ]

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook ]

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook ]

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook

State diagram for the serial adder FSM [ Figure 6. 40 from the textbook ]

State diagram for the serial adder FSM

State diagram for the serial adder FSM

State diagram for the serial adder FSM

State diagram for the serial adder FSM

State diagram for the serial adder FSM

State diagram for the serial adder FSM

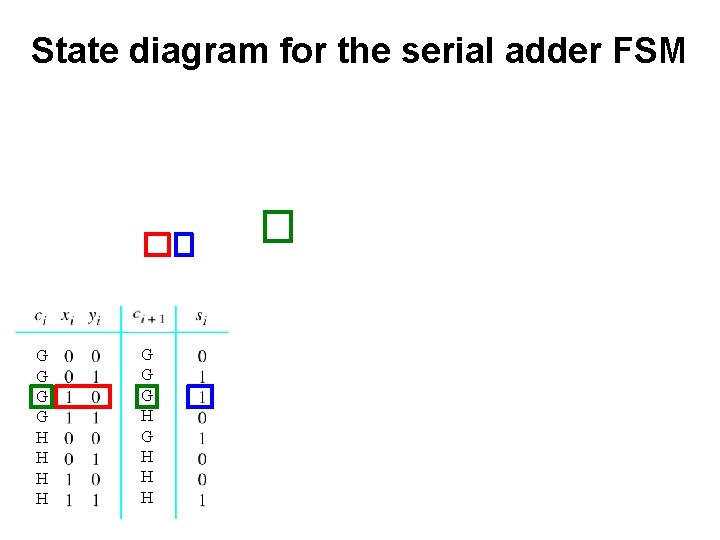
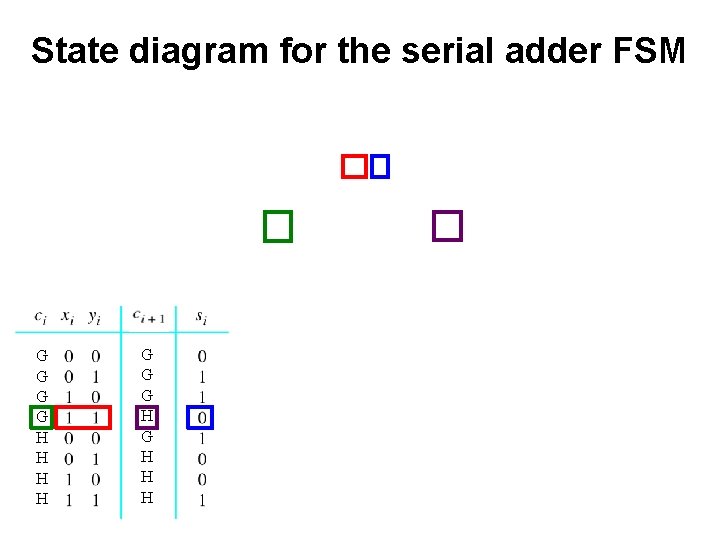
State diagram for the serial adder FSM G G H H G G G

State diagram for the serial adder FSM G G H H G G G H H H

State diagram for the serial adder FSM G G H H G G G

State diagram for the serial adder FSM G G H H G G G H H H

State diagram for the serial adder FSM G G H H G G G

State diagram for the serial adder FSM G G H H G G G H H H

State diagram for the serial adder FSM G G H H G G G

State diagram for the serial adder FSM G G H H G G G H H H

State diagram for the serial adder FSM G G H H G G G

State diagram for the serial adder FSM G G H H G G G H H H

State diagram for the serial adder FSM State table for the serial adder FSM

State diagram for the serial adder FSM State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 [ Figure 6. 40 & 6. 41 from the textbook ]

State diagram for the serial adder FSM State table for the serial adder FSM

State diagram for the serial adder FSM State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 [ Figure 6. 40 & 6. 41 from the textbook ]

State diagram for the serial adder FSM State table for the serial adder FSM

State diagram for the serial adder FSM State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 [ Figure 6. 40 & 6. 41 from the textbook ]

State table for the serial adder FSM Present state G H Output s Next

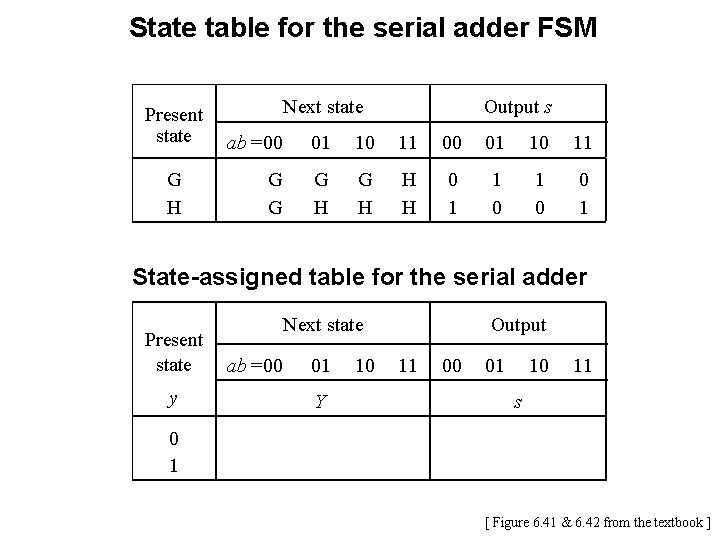
State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 [ Figure 6. 41 from the textbook ]

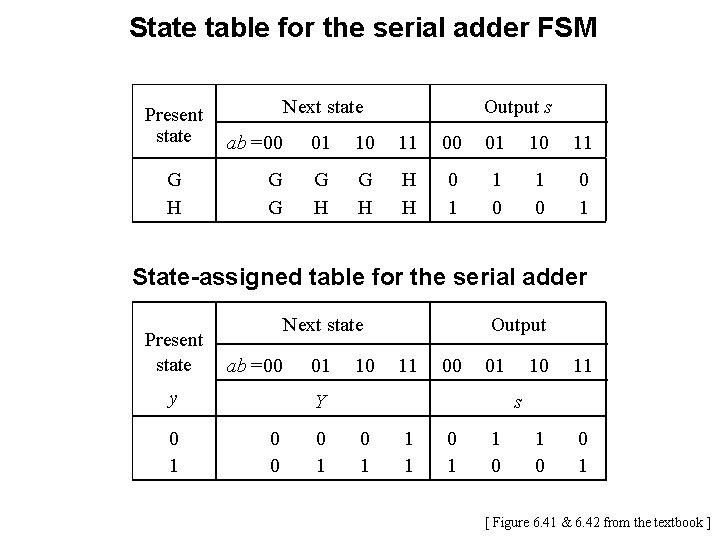
State table for the serial adder FSM Present state G H Output s Next

State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 State-assigned table for the serial adder Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 1 0 0 1 s 0 1 1 1 0 [ Figure 6. 41 & 6. 42 from the textbook ]

State table for the serial adder FSM Present state G H Output s Next

State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 State-assigned table for the serial adder Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 1 0 0 1 s 0 1 1 1 0 [ Figure 6. 41 & 6. 42 from the textbook ]

State table for the serial adder FSM Present state G H Output s Next

State table for the serial adder FSM Present state G H Output s Next state ab =00 01 10 11 G G G H H H 0 1 1 0 0 1 State-assigned table for the serial adder Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 1 0 0 1 s 0 1 1 1 0 [ Figure 6. 41 & 6. 42 from the textbook ]

Derivation of Y and s Present state Next state ab =00 y 0 1

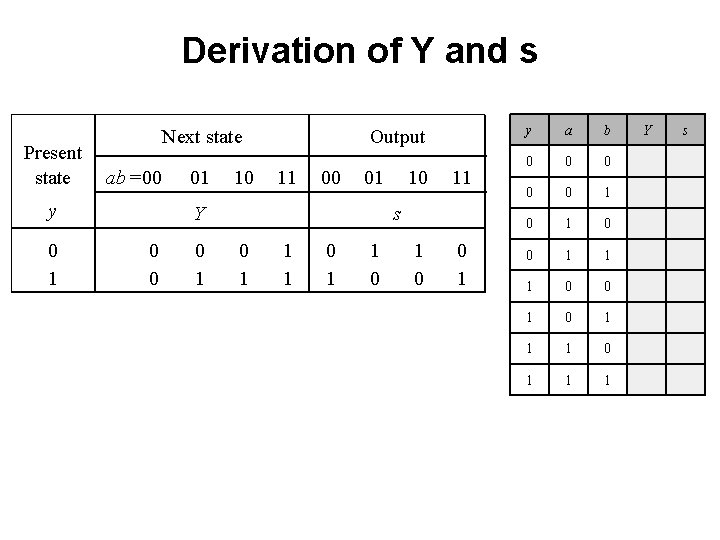
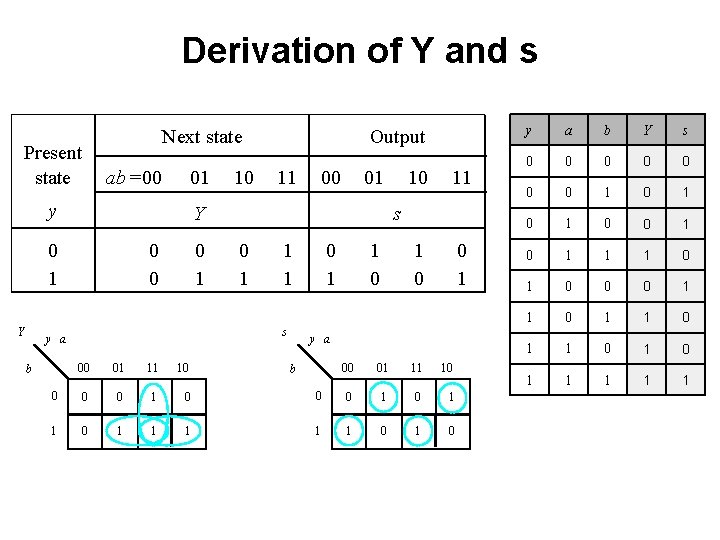
Derivation of Y and s Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 1 0 0 1 s 0 1 1 1 0

Derivation of Y and s Present state Next state ab =00 y 0 1

Derivation of Y and s Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 s 0 1 1 1 0 1 0 0 1 y a b 0 0 0 1 1 1 0 0 1 1 1 Y s

Derivation of Y and s Present state Next state ab =00 y 0 1

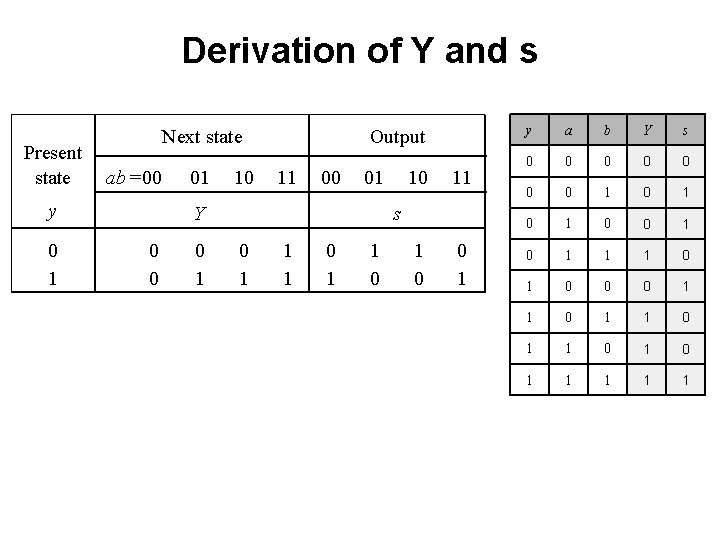
Derivation of Y and s Present state Next state ab =00 y 0 1 01 10 Output 11 00 01 Y 0 0 0 1 10 11 s 0 1 1 1 0 1 0 0 1 y a b Y s 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1

Derivation of Y and s Present state Next state ab =00 01 y 0

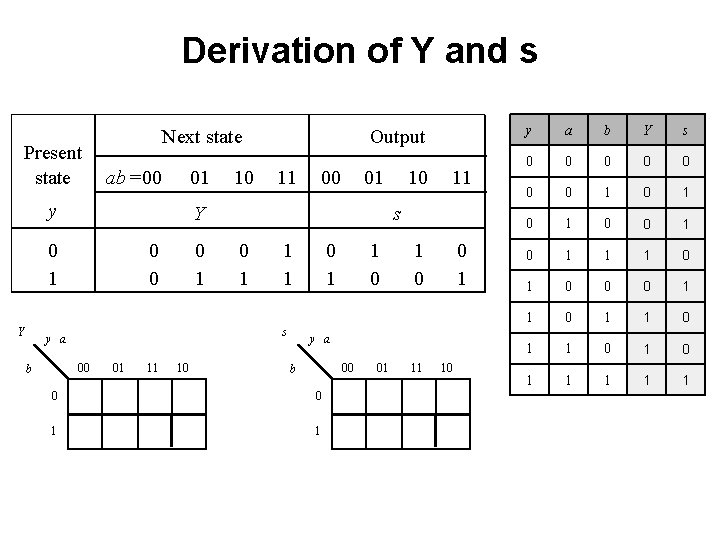
Derivation of Y and s Present state Next state ab =00 01 y 0 0 0 1 00 01 11 10 10 11 s 0 1 1 1 s y a b 11 Y 0 1 Y 10 Output 0 1 1 0 0 1 y a 00 b 0 0 1 1 01 11 10 y a b Y s 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1

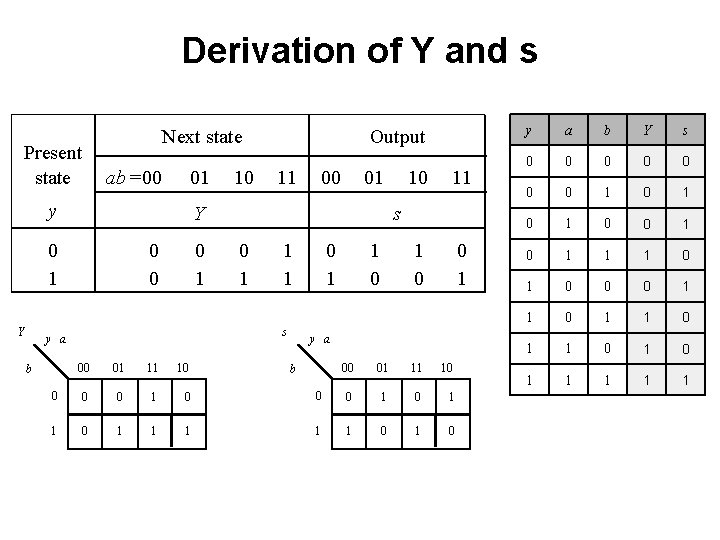
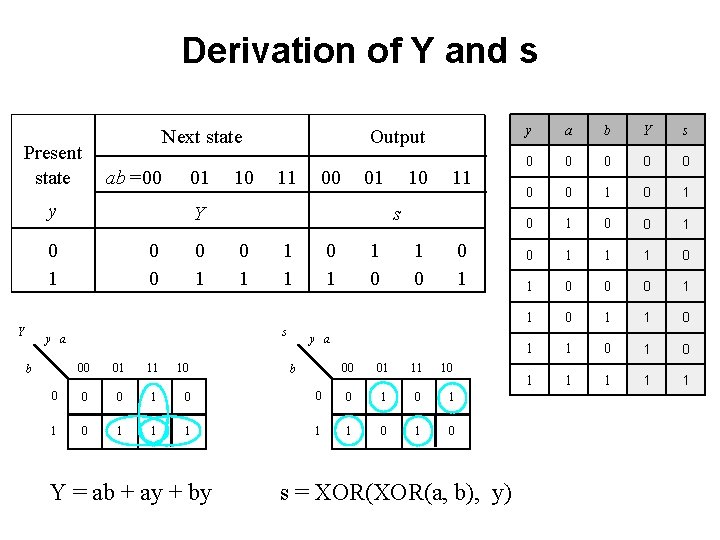
Derivation of Y and s Present state Next state ab =00 01 y 0

Derivation of Y and s Present state Next state ab =00 01 y 0 0 0 1 00 01 11 10 0 1 0 1 1 1 10 11 s 0 1 1 1 s y a b 11 Y 0 1 Y 10 Output 0 1 1 0 0 1 y a 00 01 11 10 0 0 1 1 1 0 b y a b Y s 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1

Derivation of Y and s Present state Next state ab =00 01 y 0

Derivation of Y and s Present state Next state ab =00 01 y 0 0 0 1 00 01 11 10 0 1 0 1 1 1 10 11 s 0 1 1 1 s y a b 11 Y 0 1 Y 10 Output 0 1 1 0 0 1 y a 00 01 11 10 0 0 1 1 1 0 b y a b Y s 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1

Derivation of Y and s Present state Next state ab =00 01 y 0

Derivation of Y and s Present state Next state ab =00 01 y 0 0 0 1 00 01 11 10 0 1 0 1 1 1 Y = ab + ay + by 10 11 s 0 1 1 1 s y a b 11 Y 0 1 Y 10 Output 0 1 1 0 0 1 y a 00 01 11 10 0 0 1 1 1 0 b s = XOR(a, b), y) y a b Y s 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1

Circuit for the serial adder FSM a b s Full adder Y carry-out D

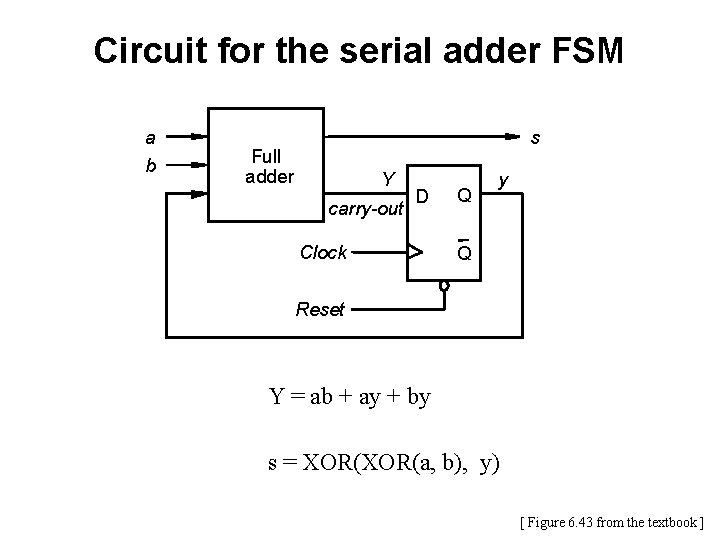
Circuit for the serial adder FSM a b s Full adder Y carry-out D Clock Q y Q Reset Y = ab + ay + by s = XOR(a, b), y) [ Figure 6. 43 from the textbook ]

Moore Machine Implementation

Moore Machine Implementation

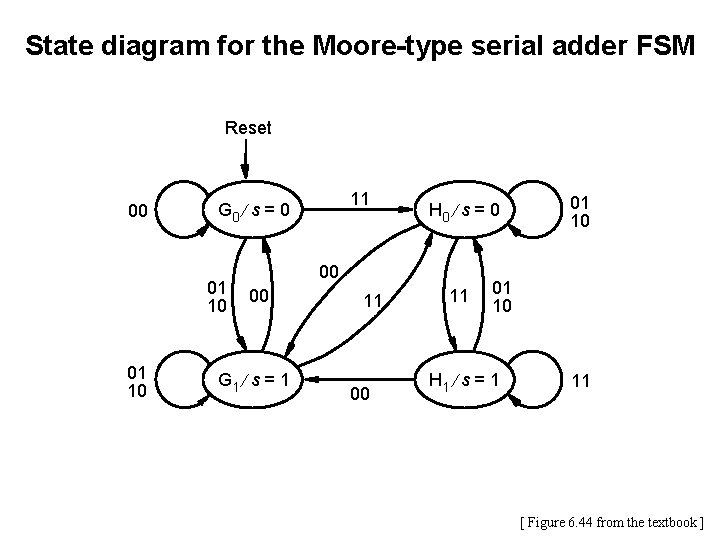
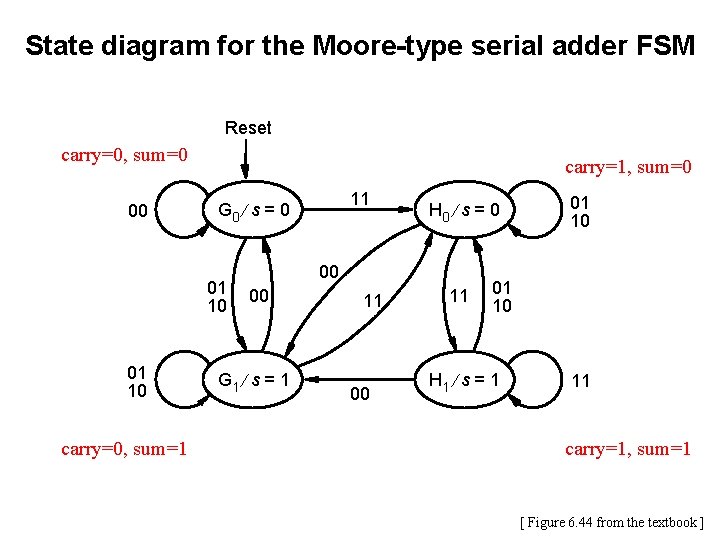
State diagram for the Moore-type serial adder FSM Reset 00 01 10 11 G

State diagram for the Moore-type serial adder FSM Reset 00 01 10 11 G 0 ¤ s = 0 H 0 ¤ s = 0 00 00 G 1 ¤ s = 1 11 00 11 01 10 H 1 ¤ s = 1 11 [ Figure 6. 44 from the textbook ]

State diagram for the Moore-type serial adder FSM Reset carry=0, sum=0 00 carry=1, sum=0

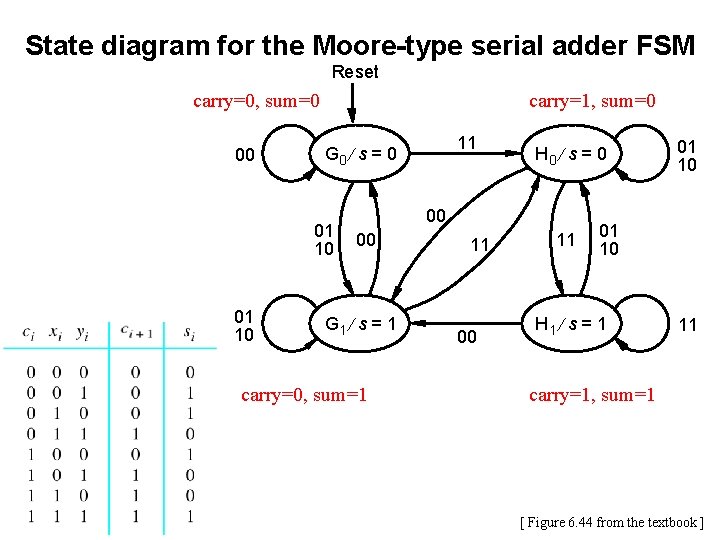
State diagram for the Moore-type serial adder FSM Reset carry=0, sum=0 00 carry=1, sum=0 01 10 carry=0, sum=1 11 G 0 ¤ s = 0 H 0 ¤ s = 0 00 00 G 1 ¤ s = 1 11 00 11 01 10 H 1 ¤ s = 1 11 carry=1, sum=1 [ Figure 6. 44 from the textbook ]

State diagram for the Moore-type serial adder FSM Reset carry=0, sum=0 00 carry=1, sum=0

State diagram for the Moore-type serial adder FSM Reset carry=0, sum=0 00 carry=1, sum=0 01 10 11 G 0 ¤ s = 0 H 0 ¤ s = 0 00 00 G 1 ¤ s = 1 carry=0, sum=1 11 00 11 01 10 H 1 ¤ s = 1 11 carry=1, sum=1 [ Figure 6. 44 from the textbook ]

State table for the Moore-type serial adder FSM Present state Nextstate ab =00 01

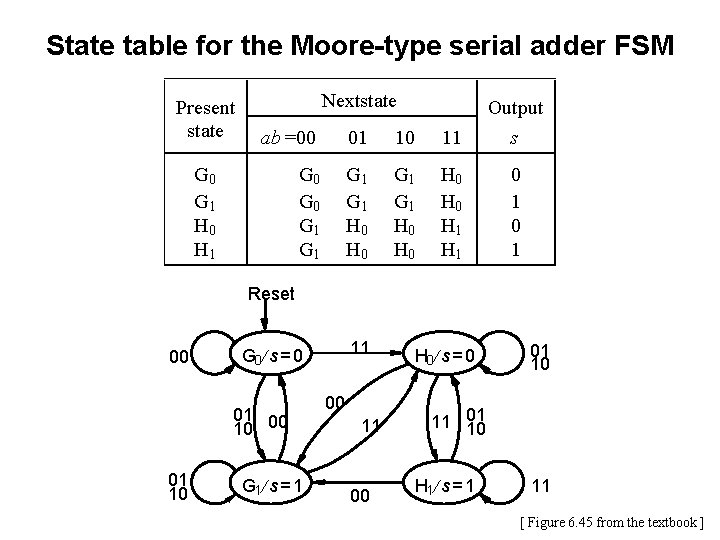
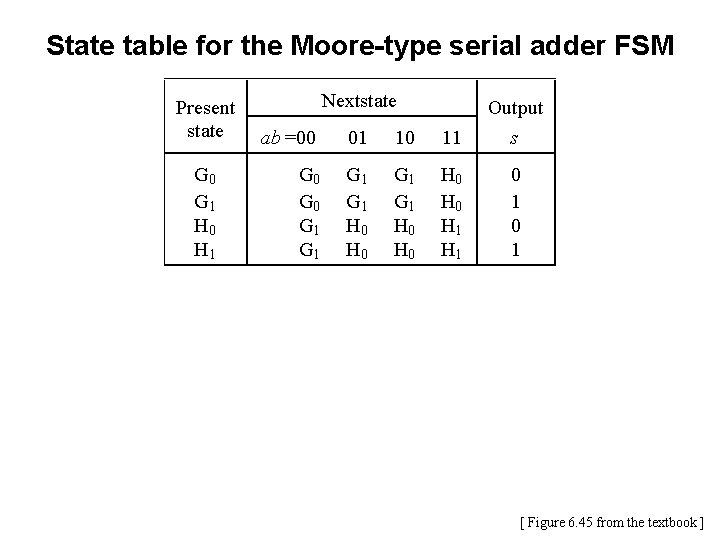
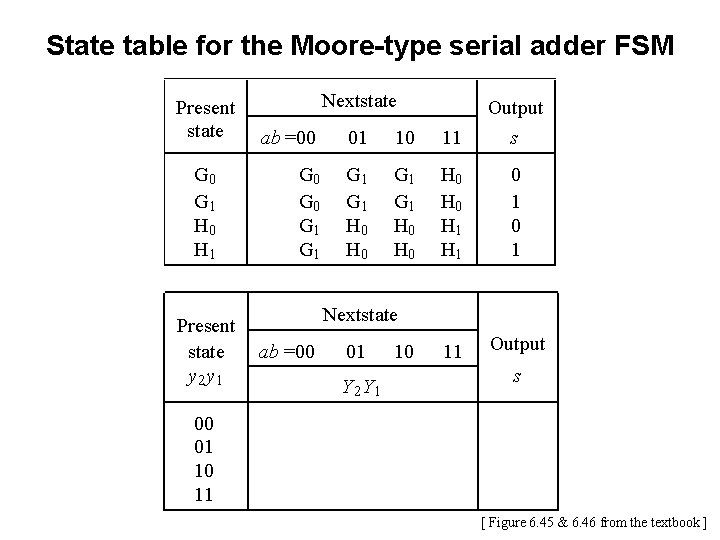
State table for the Moore-type serial adder FSM Present state Nextstate ab =00 01 10 11 Output s G 0 G 1 G 1 H 0 H 0 H 1 0 1 G 0 G 1 H 0 H 1 Reset 00 01 00 10 01 10 11 G 0 ¤ s = 0 G 1 ¤ s = 1 00 11 00 H 0 ¤ s = 0 01 10 11 01 10 H 1 ¤ s = 1 11 [ Figure 6. 45 from the textbook ]

State table for the Moore-type serial adder FSM Present state G 0 G 1

State table for the Moore-type serial adder FSM Present state G 0 G 1 H 0 H 1 Nextstate ab =00 01 10 11 Output s G 0 G 1 G 1 H 0 H 0 H 1 0 1 [ Figure 6. 45 from the textbook ]

State table for the Moore-type serial adder FSM Present state G 0 G 1

State table for the Moore-type serial adder FSM Present state G 0 G 1 H 0 H 1 Present state y 2 y 1 Nextstate ab =00 01 10 11 Output s G 0 G 1 G 1 H 0 H 0 H 1 0 1 11 Output Nextstate ab =00 01 Y 2 Y 1 10 s 00 01 10 11 [ Figure 6. 45 & 6. 46 from the textbook ]

State table for the Moore-type serial adder FSM Present state G 0 G 1

State table for the Moore-type serial adder FSM Present state G 0 G 1 H 0 H 1 Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 Output s G 0 G 1 G 1 H 0 H 0 H 1 0 1 11 Output Nextstate ab =00 01 10 s Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 [ Figure 6. 45 & 6. 46 from the textbook ]

State-assigned table for the Moore-type serial adder FSM Present state y 2 y 1

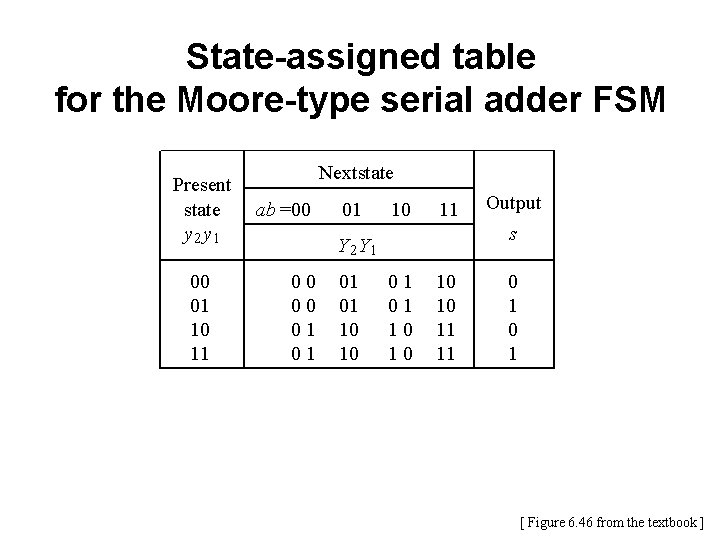
State-assigned table for the Moore-type serial adder FSM Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 [ Figure 6. 46 from the textbook ]

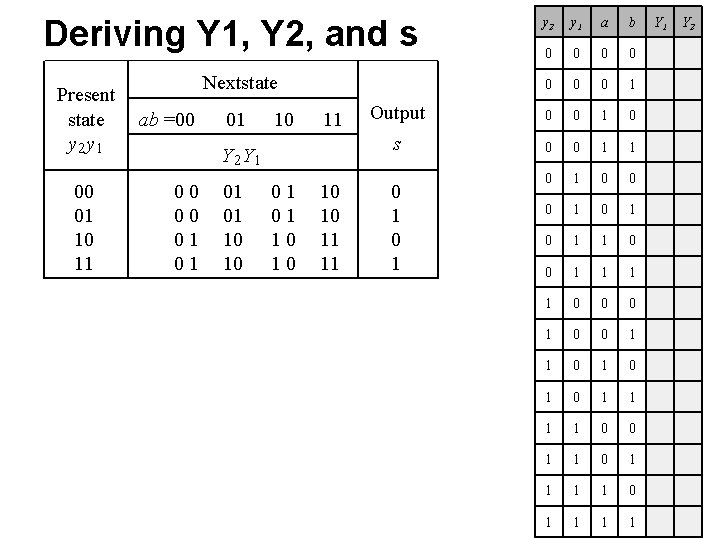
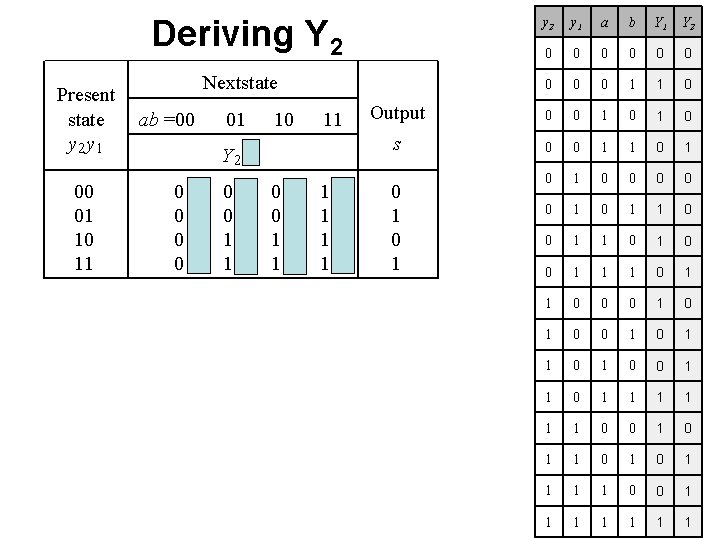
Deriving Y 1, Y 2, and s Present state y 2 y 1 00

Deriving Y 1, Y 2, and s Present state y 2 y 1 00 01 10 11 y 2 y 1 a b 0 0 0 0 1 Output 0 0 1 0 s 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 Y 2

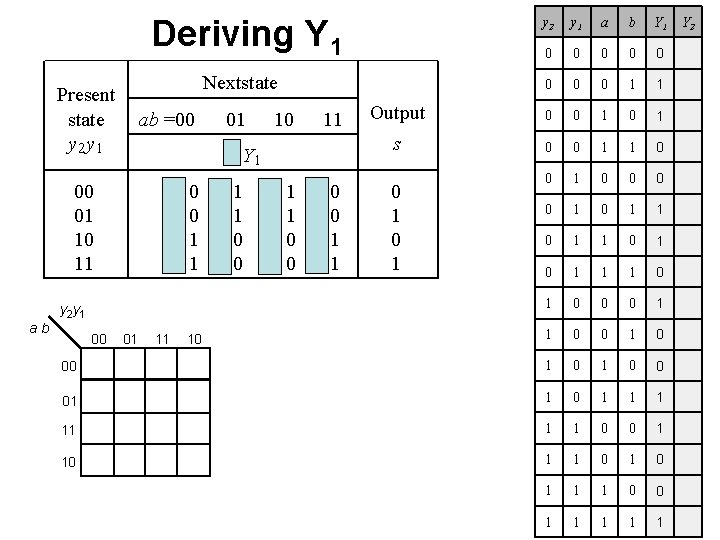
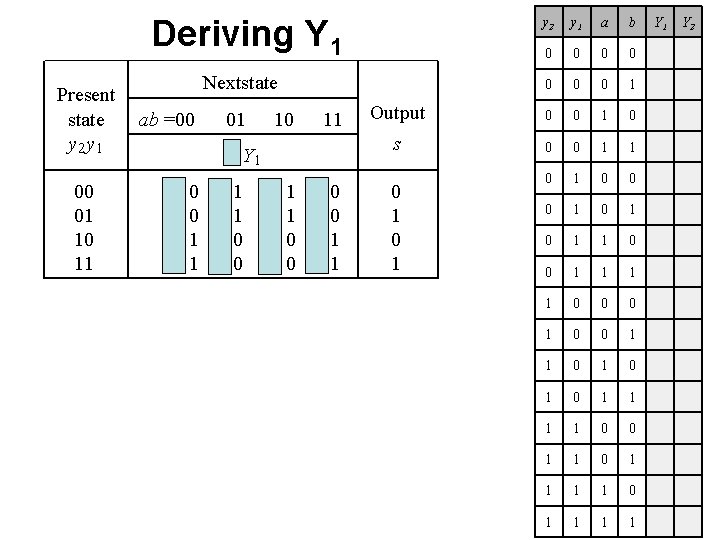
Deriving Y 1 Present state y 2 y 1 00 01 10 11 y

Deriving Y 1 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b 0 0 0 0 1 Output 0 0 1 0 s 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 Y 2

Deriving Y 1 Present state y 2 y 1 00 01 10 11 y

Deriving Y 1 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 0 0 0 0 1 1 Output 0 0 1 s 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 Y 2

Deriving Y 1 y 2 y 1 a b Y 1 0 0 0

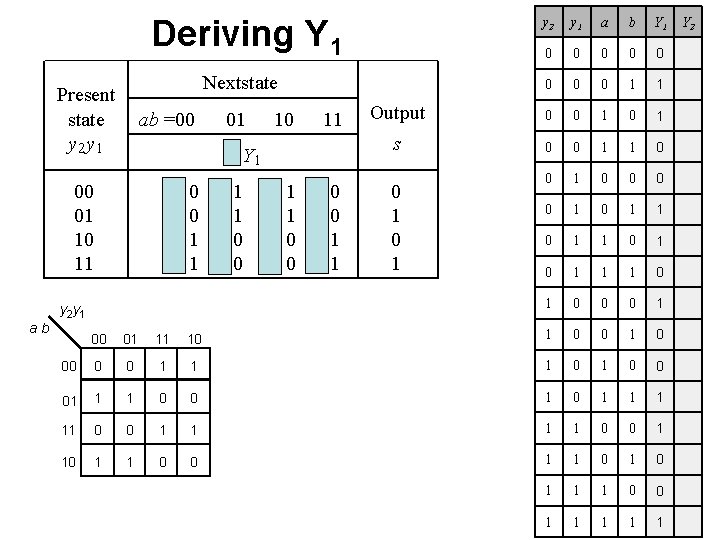
Deriving Y 1 y 2 y 1 a b Y 1 0 0 0 0 1 1 Output 0 0 1 s 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 1 0 00 1 0 0 01 1 0 1 11 1 1 0 0 1 1 1 0 0 1 1 1 Nextstate Present state y 2 y 1 ab =00 00 00 01 01 y 2 y 1 00 10 11 Y 2 Y 1 00 01 10 11 ab 01 01 11 10 01 01 10 10 11 11 0 1 Y 2

Deriving Y 1 y 1 a b Y 1 0 0 0 0 1

Deriving Y 1 y 1 a b Y 1 0 0 0 0 1 1 Output 0 0 1 s 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 Nextstate Present state y 2 y 1 ab =00 01 10 11 Y 2 Y 1 00 01 10 11 00 00 01 01 y 2 y 1 ab y 2 01 01 10 10 11 11 0 1 00 01 11 10 1 0 00 0 0 1 1 1 0 0 01 1 1 0 0 1 1 1 11 0 0 1 1 0 0 1 1 1 0 0 1 1 1 Y 2

Deriving Y 1 y 1 a b Y 1 0 0 0 0 1

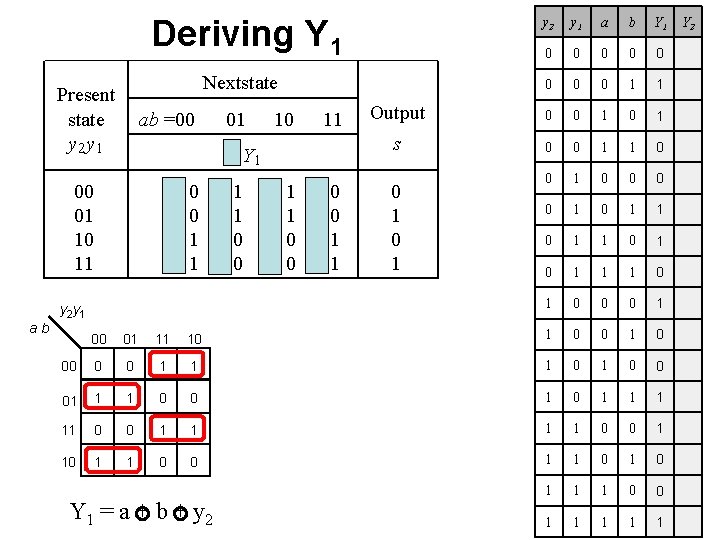
Deriving Y 1 y 1 a b Y 1 0 0 0 0 1 1 Output 0 0 1 s 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 Nextstate Present state y 2 y 1 ab =00 01 10 11 Y 2 Y 1 00 01 10 11 00 00 01 01 y 2 y 1 ab y 2 01 01 10 10 11 11 0 1 00 01 11 10 1 0 00 0 0 1 1 1 0 0 01 1 1 0 0 1 1 1 11 0 0 1 1 0 0 1 1 1 0 0 1 1 1 Y 1 = a + b + y 2 Y 2

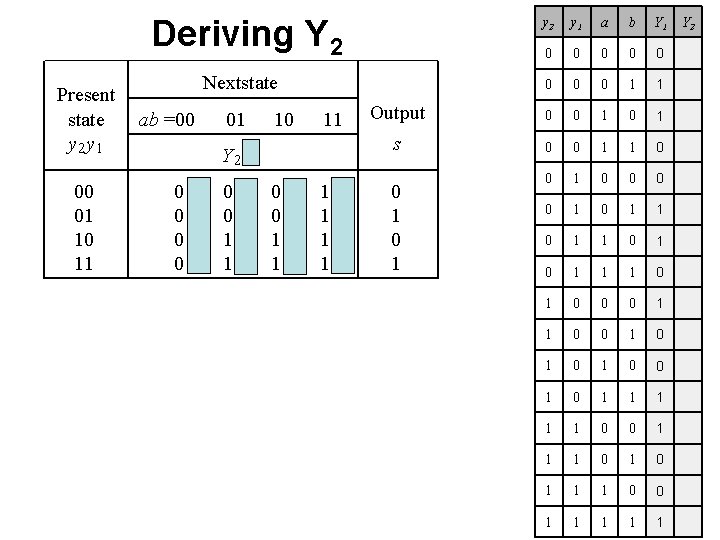
Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 0 0 0 0 1 1 Output 0 0 1 s 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 Y 2

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 Y 2 0 0 0 0 0 1 1 0 Output 0 0 1 0 s 0 0 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 0 0 1 1 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

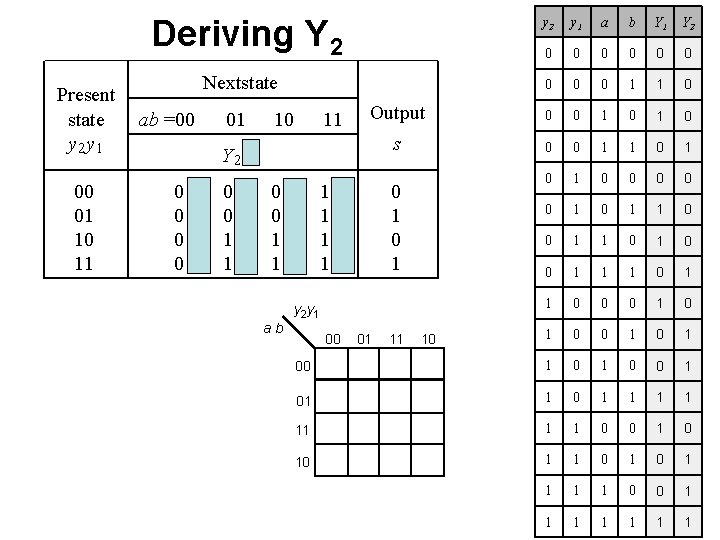
Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 Y 2 0 0 0 0 0 1 1 0 Output 0 0 1 0 s 0 0 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 00 1 01 1 0 1 1 11 1 1 0 0 10 1 1 0 0 1 1 1 1 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 y 2 y 1 ab 00 01 11 10

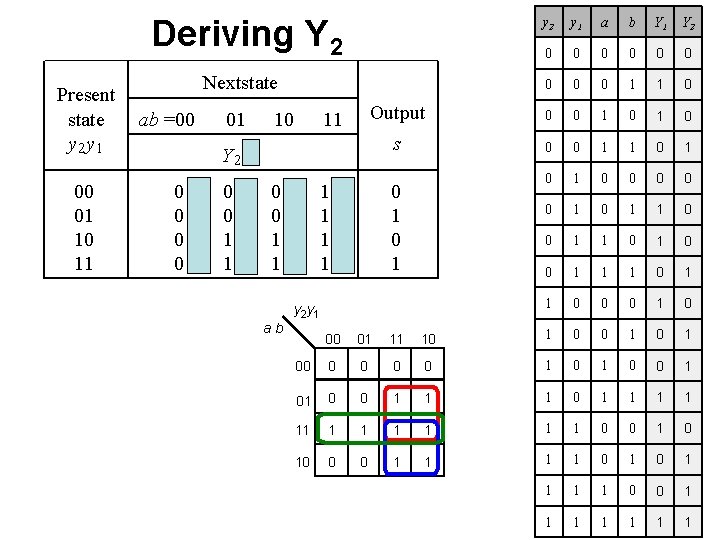
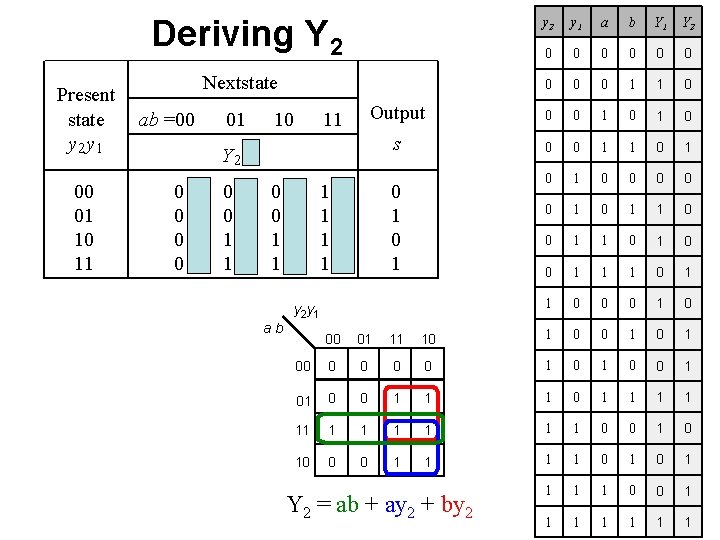
Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 Y 2 0 0 0 0 0 1 1 0 Output 0 0 1 0 s 0 0 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 y 2 y 1 ab 00 01 11 10 1 0 1 00 0 0 1 01 0 0 1 1 1 1 11 1 1 1 0 0 10 0 0 1 1 1 1 0 0 1 1 1 1

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 Y 2 0 0 0 0 0 1 1 0 Output 0 0 1 0 s 0 0 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 y 2 y 1 ab 00 01 11 10 1 0 1 00 0 0 1 01 0 0 1 1 1 1 11 1 1 1 0 0 10 0 0 1 1 1 1 0 0 1 1 1 1

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y

Deriving Y 2 Present state y 2 y 1 00 01 10 11 y 2 y 1 a b Y 1 Y 2 0 0 0 0 0 1 1 0 Output 0 0 1 0 s 0 0 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 Nextstate ab =00 01 10 11 Y 2 Y 1 00 00 01 01 10 10 11 11 0 1 y 2 y 1 ab 00 01 11 10 1 0 1 00 0 0 1 01 0 0 1 1 1 1 11 1 1 1 0 0 10 0 0 1 1 1 1 0 0 1 1 1 1 Y 2 = ab + ay 2 + by 2

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab

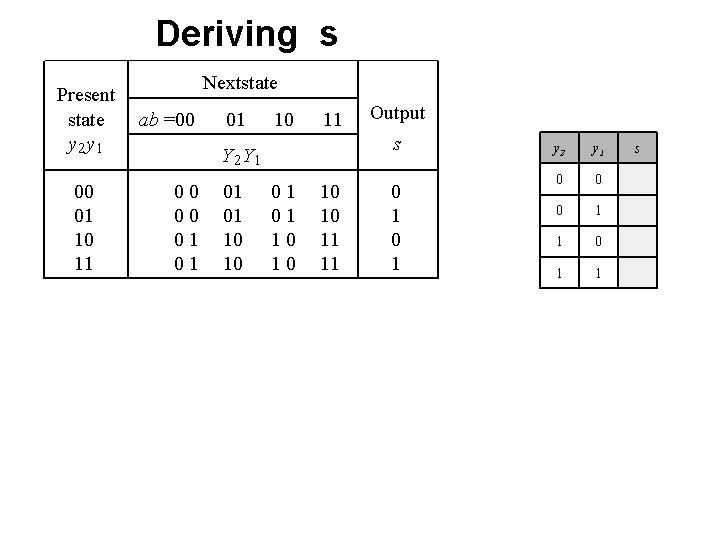
Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 y 2 y 1 0 0 0 1 1 s

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 y 2 y 1 s 0 0 1 1 1

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab

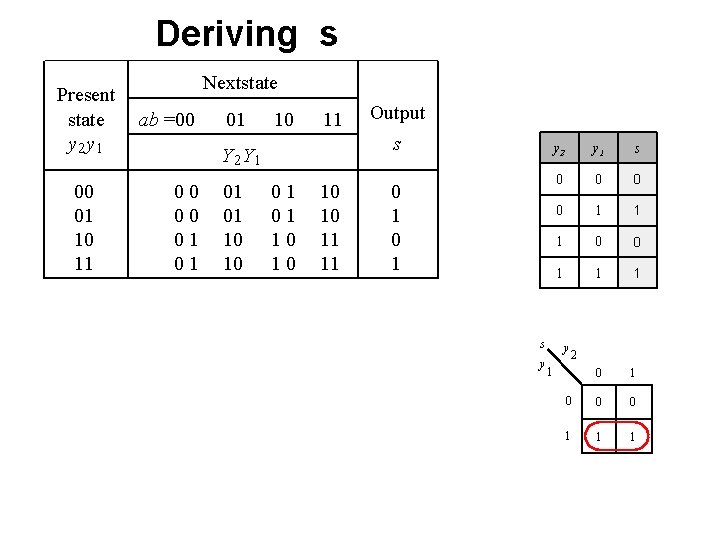
Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 s y y 2 y 1 s 0 0 1 1 1 0 1 y 2 1 0 1

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 s y y 2 y 1 s 0 0 1 1 1 0 0 0 1 1 1 y 2 1

Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab

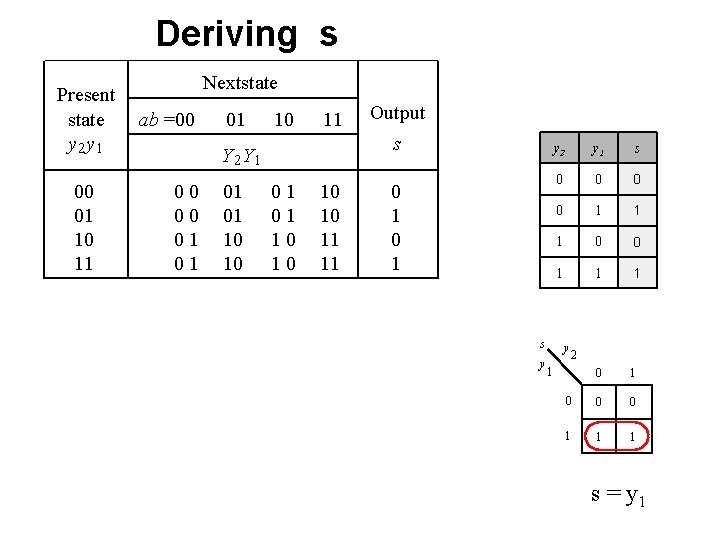
Deriving s Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 s y y 2 y 1 s 0 0 1 1 1 0 0 0 1 1 1 y 2 1 s = y 1

State-assigned table for the Moore-type serial adder FSM Present state y 2 y 1

State-assigned table for the Moore-type serial adder FSM Present state y 2 y 1 00 01 10 11 Nextstate ab =00 01 10 11 s Y 2 Y 1 00 00 01 01 10 10 Output 01 01 10 10 11 11 0 1 Y 1 = a + b + y 2 Y 2 = ab + ay 2 + by 2 s = y 1 [ Figure 6. 46 from the textbook ]

Circuit for the Moore-type serial adder FSM a b Sum bit Full adder Y

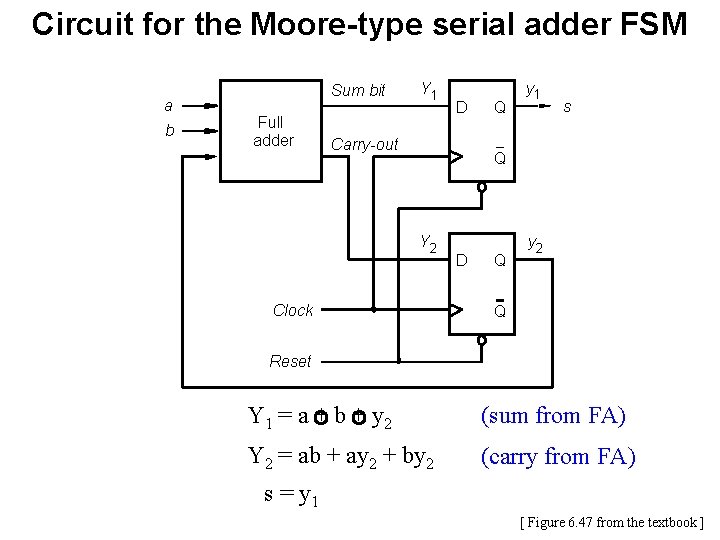
Circuit for the Moore-type serial adder FSM a b Sum bit Full adder Y 1 D Carry-out Q y 1 s Q Y 2 Clock D Q y 2 Q Reset Y 1 = a + b + y 2 (sum from FA) Y 2 = ab + ay 2 + by 2 (carry from FA) s = y 1 [ Figure 6. 47 from the textbook ]

Questions?

Questions?

THE END

THE END