Cpr E 281 Digital Logic Instructor Alexander Stoytchev

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Signed Numbers Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • HW 5 is out • It is due on Monday Oct 6 @ 4 pm. • Please write clearly on the first page (in block capital letters) the following three things: § Your First and Last Name § Your Student ID Number § Your Lab Section Letter

Administrative Stuff • Labs Next Week • Mini-Project • This one is worth 3% of your grade. • Make sure to get all the points. • http: //www. ece. iastate. edu/~alexs/classes/2014_Fall_ 281/labs/Project-Mini/

Quick Review

Adding two bits (there are four possible cases) [ Figure 3. 1 a from the textbook ]

Adding two bits (the truth table) [ Figure 3. 1 b from the textbook ]

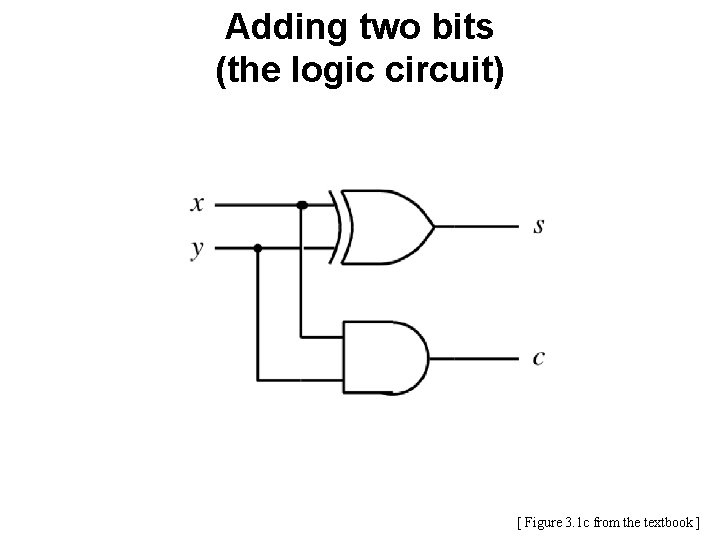
Adding two bits (the logic circuit) [ Figure 3. 1 c from the textbook ]

The Half-Adder [ Figure 3. 1 c-d from the textbook ]

Addition of multibit numbers Bit position i [ Figure 3. 2 from the textbook ]

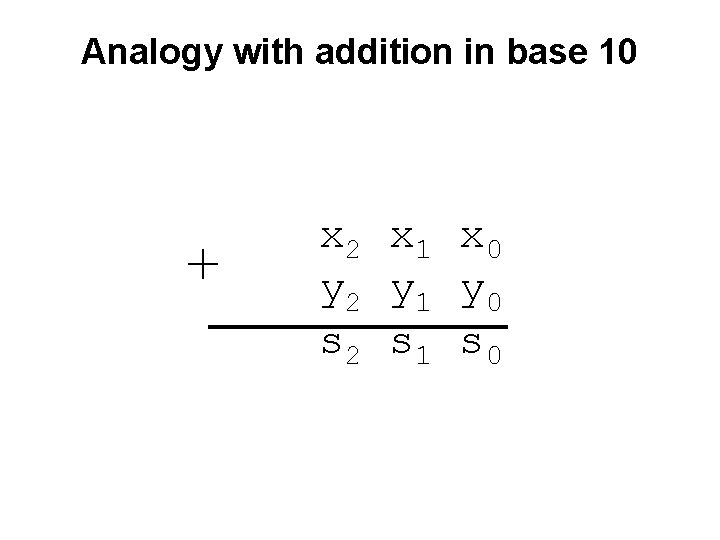
Analogy with addition in base 10 + c 3 c 2 x 2 y 2 s 2 c 1 x 1 y 1 s 1 c 0 x 0 y 0 s 0

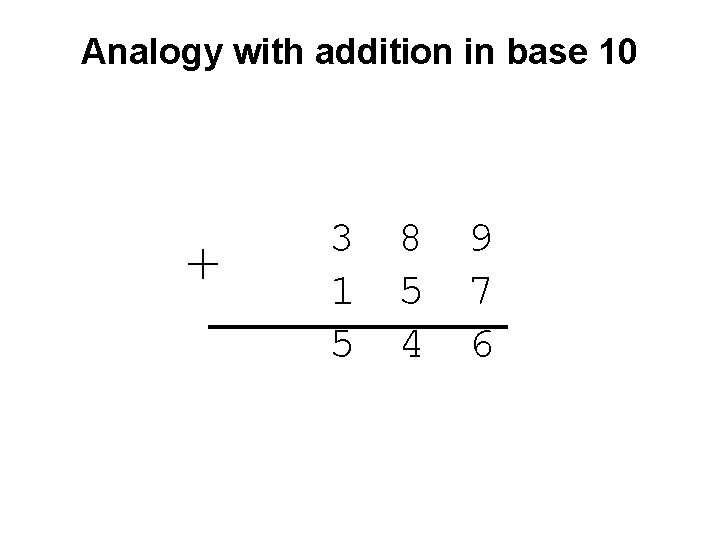
Analogy with addition in base 10 + 3 8 9 1 5 7 5 4 6

Analogy with addition in base 10 carry + 0 1 3 1 5 1 8 5 4 0 9 7 6

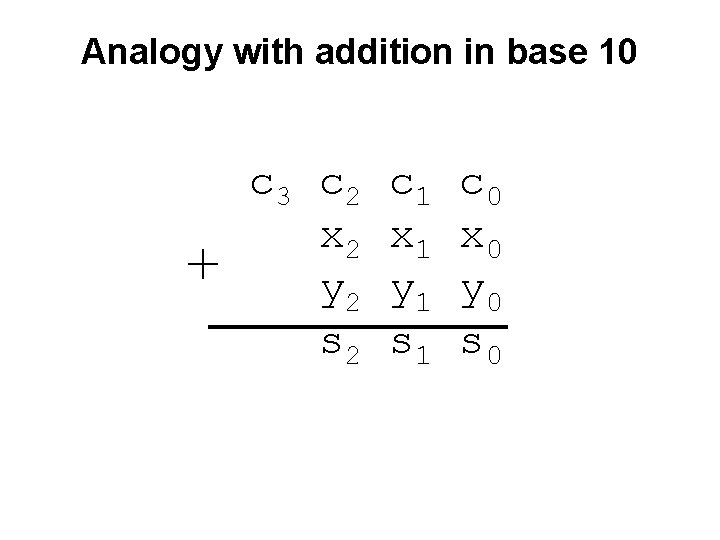
Analogy with addition in base 10 + c 3 c 2 x 2 y 2 s 2 c 1 x 1 y 1 s 1 c 0 x 0 y 0 s 0

Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ] [ Figure 3. 3 a from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

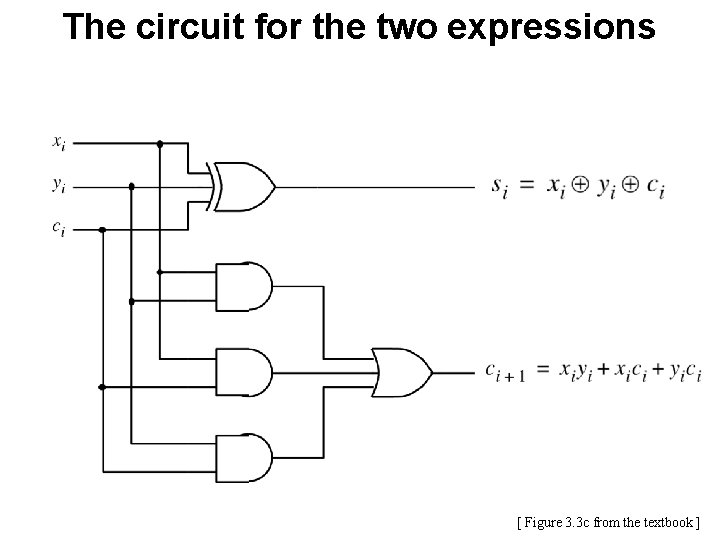
The circuit for the two expressions [ Figure 3. 3 c from the textbook ]

This is called the Full-Adder [ Figure 3. 3 c from the textbook ]

XOR Magic (si can be implemented in two different ways)

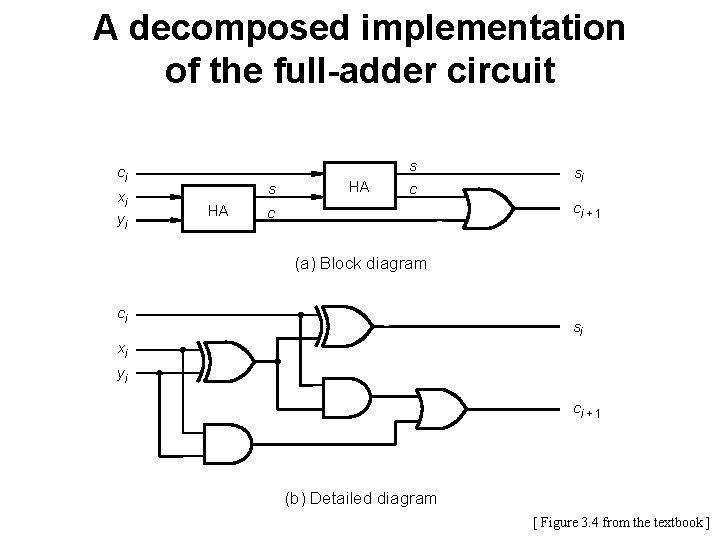
A decomposed implementation of the full-adder circuit s ci xi yi s HA HA c si ci + 1 c (a) Block diagram ci si xi yi ci + 1 (b) Detailed diagram [ Figure 3. 4 from the textbook ]

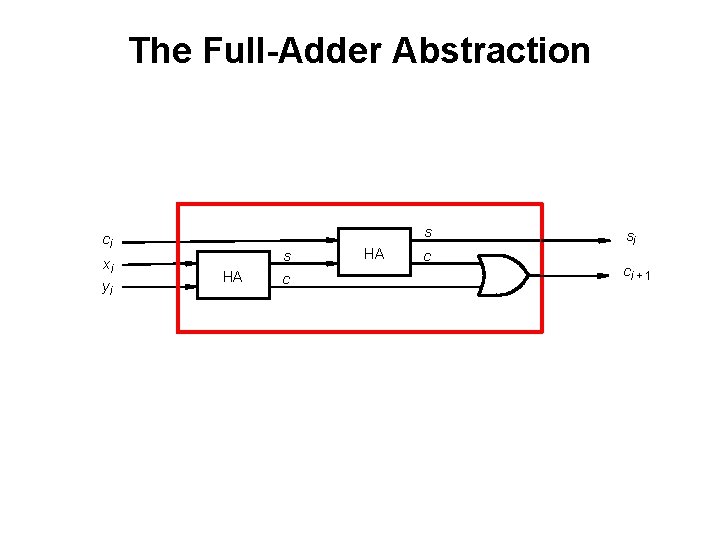
The Full-Adder Abstraction s ci xi yi s HA c si ci + 1

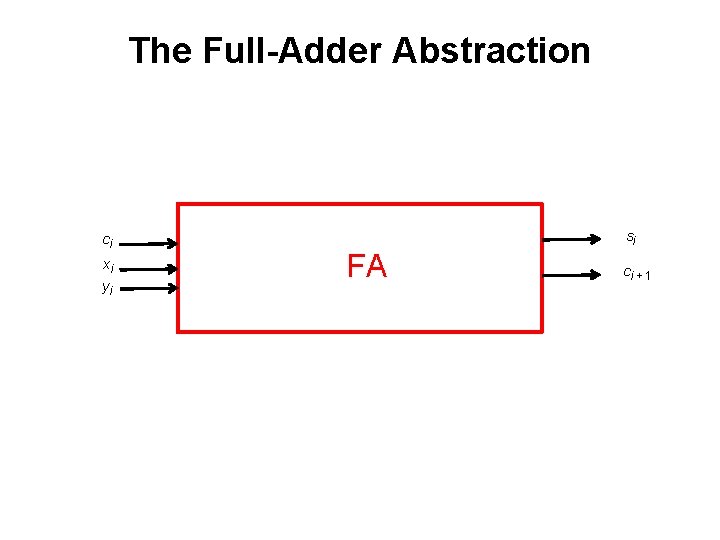
The Full-Adder Abstraction ci xi yi si FA ci + 1

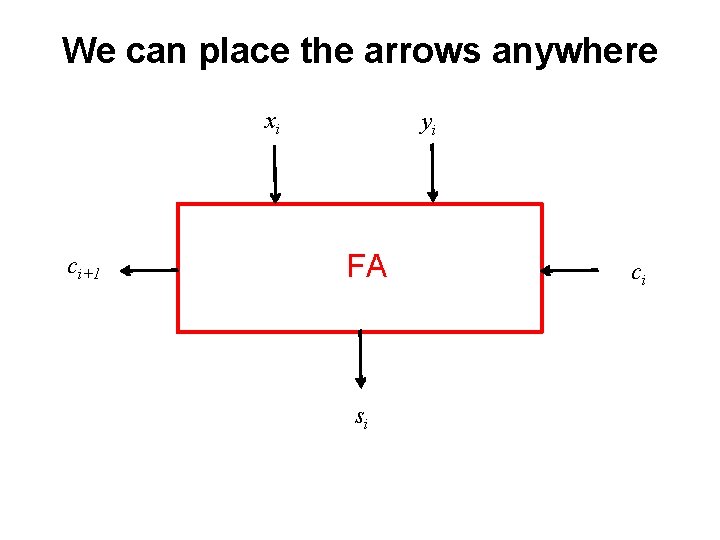
We can place the arrows anywhere xi ci+1 yi FA si ci

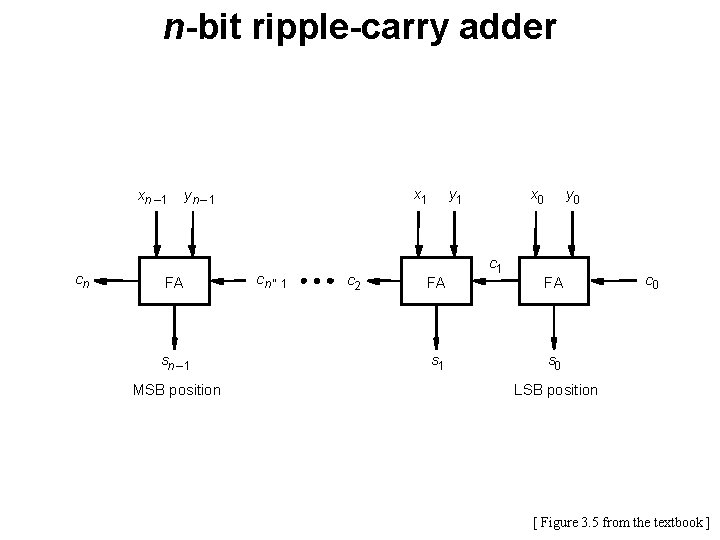
n-bit ripple-carry adder xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn ” 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA c 0 s 0 LSB position [ Figure 3. 5 from the textbook ]

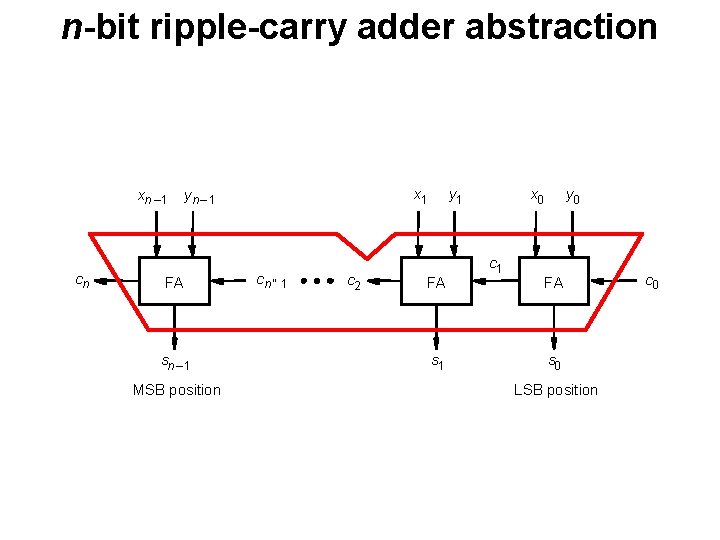
n-bit ripple-carry adder abstraction xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn ” 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA s 0 LSB position c 0

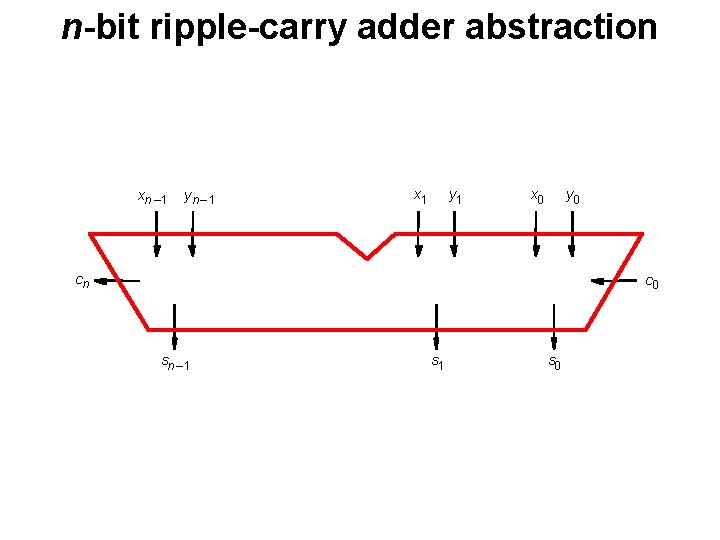
n-bit ripple-carry adder abstraction xn – 1 yn – 1 x 1 y 1 x 0 y 0 cn c 0 sn – 1 s 0

The x and y lines are typically grouped together for better visualization, but the underlying logic remains the same xn – 1 x 0 yn – 1 y 0 cn c 0 sn – 1 s 0

Math Review: Subtraction - 39 15 ? ?

Math Review: Subtraction - 39 15 24

Math Review: Subtraction - 82 61 ? ? - 48 26 ? ? - 32 11 ? ?

Math Review: Subtraction - 82 61 21 - 48 26 22 - 32 11 21

Math Review: Subtraction - 82 64 ? ? - 48 29 ? ? - 32 13 ? ?

Math Review: Subtraction - 82 64 18 - 48 29 19 - 32 13 19

The problems in which row are easier to calculate? - 82 61 ? ? - 82 64 ? ? - 48 26 ? ? - 48 29 ? ? - 32 11 ? ? - 32 13 ? ?

The problems in which row are easier to calculate? - 82 61 21 - 48 26 22 - 48 29 19 - 32 11 21 - 32 13 19 Why? - 82 64 18

Another Way to Do Subtraction 82 – 64 = 82 + 100 – 100 - 64

Another Way to Do Subtraction 82 – 64 = 82 + 100 – 100 - 64 = 82 + (100 – 64) - 100

Another Way to Do Subtraction 82 – 64 = 82 + 100 – 100 - 64 = 82 + (100 – 64) - 100 = 82 + (99 + 1 – 64) - 100

Another Way to Do Subtraction 82 – 64 = 82 + 100 – 100 - 64 = 82 + (100 – 64) - 100 = 82 + (99 + 1 – 64) - 100 = 82 + (99 – 64) +1 - 100

Another Way to Do Subtraction 82 – 64 = 82 + 100 – 100 - 64 = 82 + (100 – 64) - 100 = 82 + (99 + 1 – 64) - 100 Does not require borrows = 82 + (99 – 64) +1 - 100

9’s Complement (subtract each digit from 9) - 99 64 35

10’s Complement (subtract each digit from 9 and add 1 to the result) - 99 64 35 + 1 = 36

Another Way to Do Subtraction 82 – 64 = 82 + (99 – 64) +1 - 100

Another Way to Do Subtraction 9’s complement 82 – 64 = 82 + (99 – 64) +1 - 100

Another Way to Do Subtraction 9’s complement 82 – 64 = 82 + (99 – 64) +1 - 100 = 82 + 35 + 1 - 100

Another Way to Do Subtraction 9’s complement 82 – 64 = 82 + (99 – 64) +1 - 100 10’s complement = 82 + 35 + 1 - 100

Another Way to Do Subtraction 9’s complement 82 – 64 = 82 + (99 – 64) +1 - 100 10’s complement = 82 + 35 + 1 - 100 = 82 + 36 - 100 // add the first two

Another Way to Do Subtraction 9’s complement 82 – 64 = 82 + (99 – 64) +1 - 100 10’s complement = 82 + 35 + 1 - 100 = 82 + 36 - 100 = 118 - 100 = 18 // add the first two // delete the leading 1

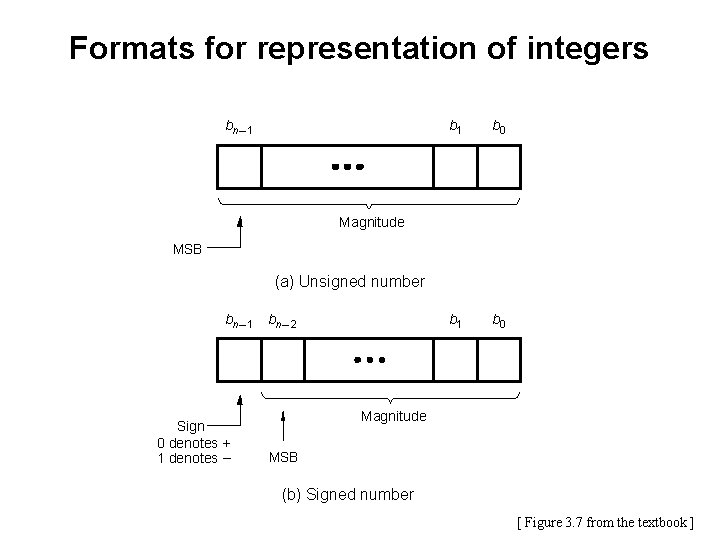
Formats for representation of integers bn – 1 b 0 b 1 b 0 Magnitude MSB (a) Unsigned number bn – 1 bn – 2 Sign 0 denotes + 1 denotes – Magnitude MSB (b) Signed number [ Figure 3. 7 from the textbook ]

Negative numbers can be represented in following ways • Sign and magnitude • 1’s complement • 2’s complement

1’s complement Let K be the negative equivalent of an n-bit positive number P. Then, in 1’s complement representation K is obtained by subtracting P from 2 n – 1, namely K = (2 n – 1) – P This means that K can be obtained by inverting all bits of P.

Find the 1’s complement of … 0101 0010 0011 0111

Find the 1’s complement of … 0101 1010 0010 1101 0011 1100 0111 1000 Just flip 1's to 0's and vice versa.

Example of 1’s complement addition (+ 5) + (+ 2) (+ 7) 0101 +0010 0111

Example of 1’s complement addition (– 5 ) + (+ 2) (- 3 ) 1010 +0010 1100 [ Figure 3. 8 from the textbook ]

Example of 1’s complement addition (+ 5) + (– 2) (+ 3) 0101 +1101 10010 1 0011 [ Figure 3. 8 from the textbook ]

Example of 1’s complement addition (– 5 ) + (– 2 ) (– 7 ) 1010 +1101 1 0111 1 1000 [ Figure 3. 8 from the textbook ]

2’s complement Let K be the negative equivalent of an n-bit positive number P. Then, in 2’s complement representation K is obtained by subtracting P from 2 n , namely K = 2 n – P

Deriving 2’s complement For a positive n-bit number P, let K 1 and K 2 denote its 1’s and 2’s complements, respectively. K 1 = (2 n – 1) – P K 2 = 2 n – P Since K 2 = K 1 + 1, it is evident that in a logic circuit the 2’s complement can computed by inverting all bits of P and then adding 1 to the resulting 1’s-complement number.

Find the 2’s complement of … 0101 0010 0011 0111

Find the 2’s complement of … 0101 1011 0010 0011 0111 1001 1110

Quick Way to find 2’s complement • Scan the binary number from right to left • Copy all bits that are 0 from right to left • Stop at the first 1 • Copy that 1 as well • Invert all remaining bits

Interpretation of four-bit signed integers [ Table 3. 2 from the textbook ]

Example of 2’s complement addition ( + 5) + ( + 2) 0101 + 0010 ( + 7) 0111 [ Figure 3. 9 from the textbook ]

Example of 2’s complement addition (– 5) + ( + 2) 1011 + 0010 (– 3) 1101 [ Figure 3. 9 from the textbook ]

Example of 2’s complement addition ( + 5) + (– 2) 0101 + 1110 ( + 3) 10011 ignore [ Figure 3. 9 from the textbook ]

Example of 2’s complement addition (– 5) + (– 2) 1011 + 1110 (– 7) 11 0 0 1 ignore [ Figure 3. 9 from the textbook ]

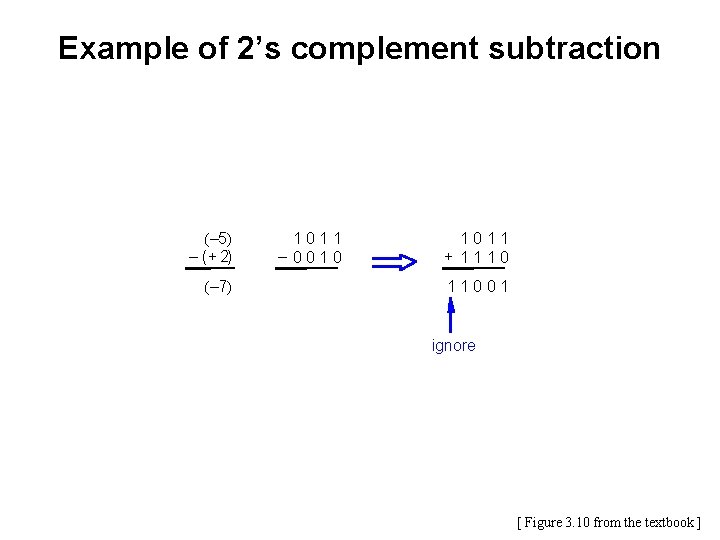
Example of 2’s complement subtraction ( + 5) – ( + 2) ( + 3) 0101 – 0010 0101 + 1110 10011 ignore [ Figure 3. 10 from the textbook ]

Example of 2’s complement subtraction (– 5) – ( + 2) (– 7) 1011 – 0010 1011 + 1110 11001 ignore [ Figure 3. 10 from the textbook ]

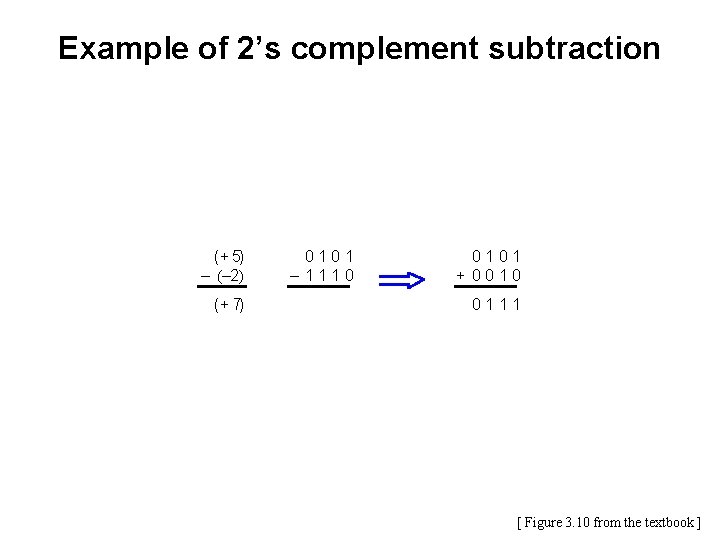
Example of 2’s complement subtraction ( + 5) – (– 2) ( + 7) 0101 – 1110 0101 + 0010 0111 [ Figure 3. 10 from the textbook ]

Example of 2’s complement subtraction (– 5) – (– 2) (– 3) 1011 – 1110 1011 + 0010 1101 [ Figure 3. 10 from the textbook ]

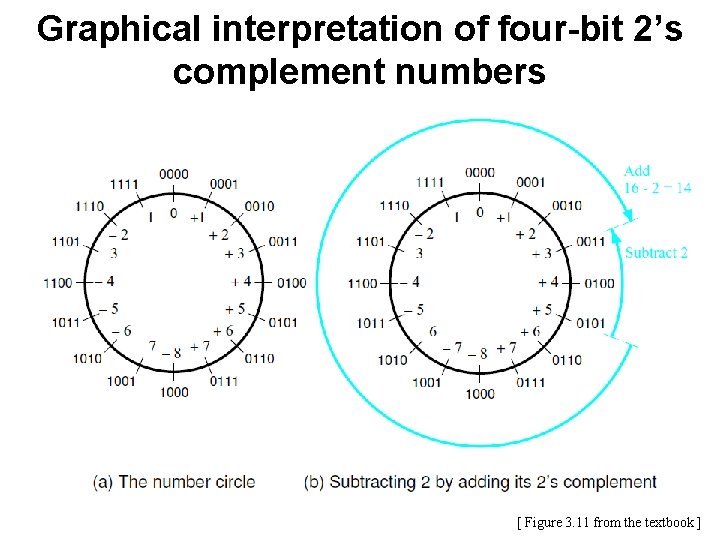
Graphical interpretation of four-bit 2’s complement numbers [ Figure 3. 11 from the textbook ]

Take-Home Message • Subtraction can be performed by simply adding the 2’s complement of the second number, regardless of the signs of the two numbers. • Thus, the same adder circuit can be used to perform both addition and subtraction !!!

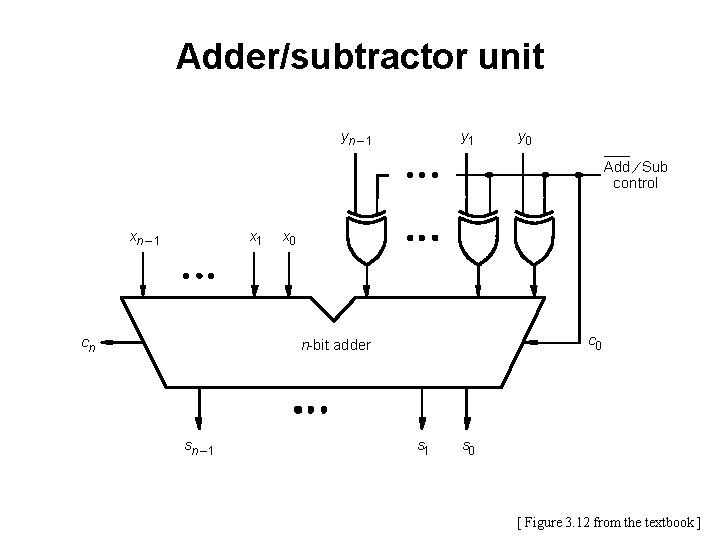
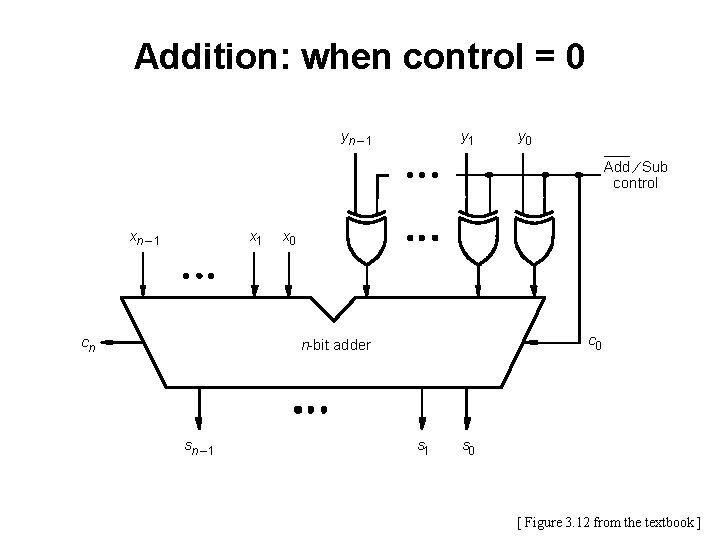
Adder/subtractor unit yn – 1 y 0 Add ¤ Sub control xn – 1 x 1 cn x 0 c 0 n-bit adder sn – 1 s 0 [ Figure 3. 12 from the textbook ]

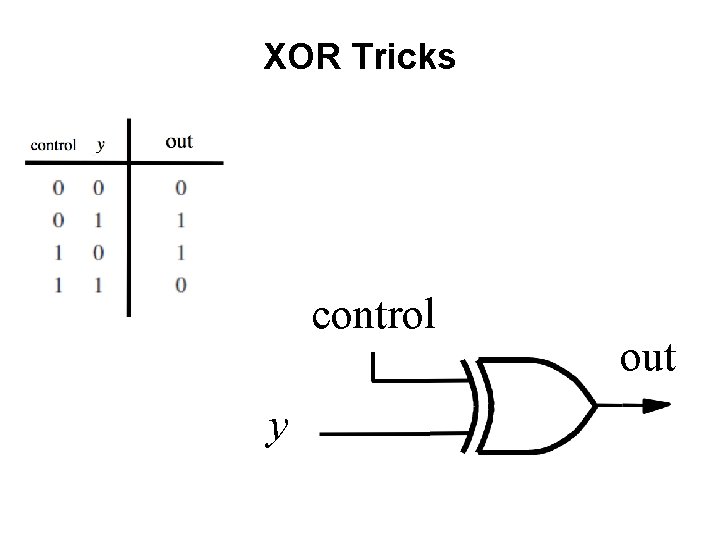
XOR Tricks control y out

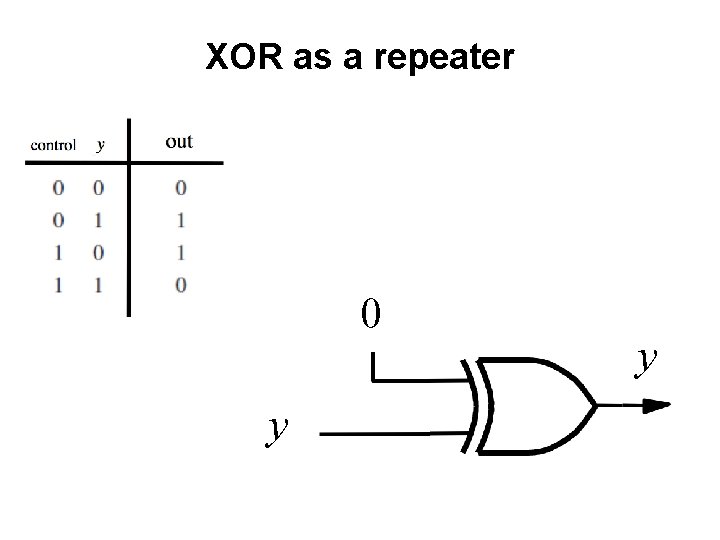
XOR as a repeater 0 y y

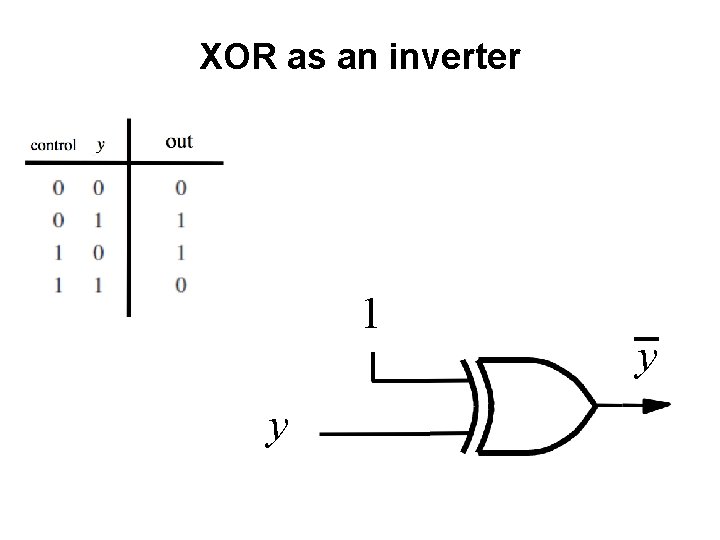
XOR as an inverter 1 y y

Addition: when control = 0 yn – 1 y 0 Add ¤ Sub control xn – 1 x 1 cn x 0 c 0 n-bit adder sn – 1 s 0 [ Figure 3. 12 from the textbook ]

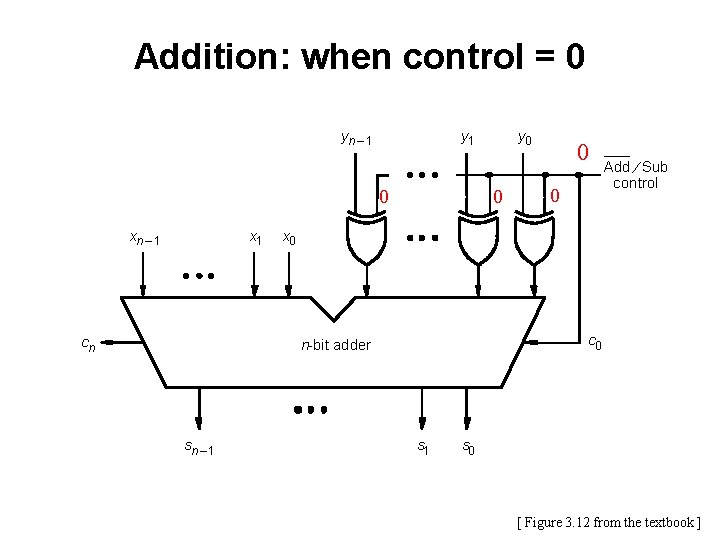
Addition: when control = 0 yn – 1 y 1 0 xn – 1 x 1 cn 0 0 0 Add ¤ Sub control x 0 c 0 n-bit adder sn – 1 y 0 s 1 s 0 [ Figure 3. 12 from the textbook ]

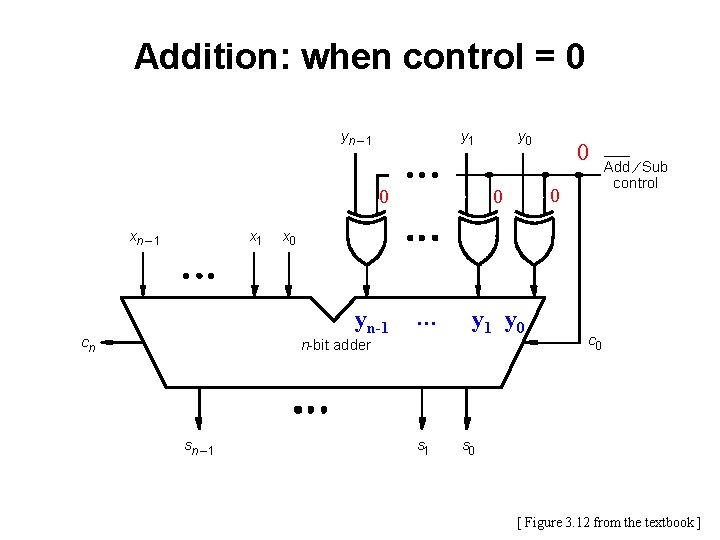
Addition: when control = 0 yn – 1 y 1 0 xn – 1 x 1 0 0 … n-bit adder sn – 1 0 Add ¤ Sub control x 0 yn-1 cn y 0 s 1 y 0 c 0 s 0 [ Figure 3. 12 from the textbook ]

Subtraction: when control = 1 yn – 1 y 0 Add ¤ Sub control xn – 1 x 1 cn x 0 c 0 n-bit adder sn – 1 s 0 [ Figure 3. 12 from the textbook ]

Subtraction: when control = 1 yn – 1 y 1 1 xn – 1 x 1 cn 1 1 1 Add ¤ Sub control x 0 c 0 n-bit adder sn – 1 y 0 s 1 s 0 [ Figure 3. 12 from the textbook ]

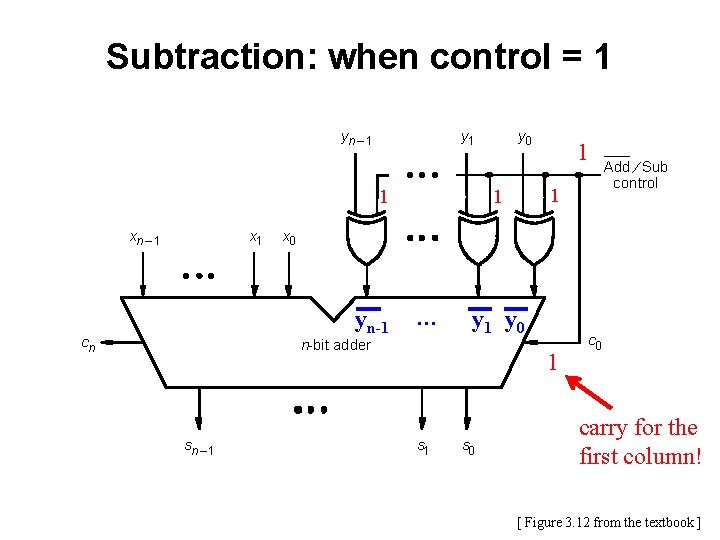
Subtraction: when control = 1 yn – 1 y 1 1 xn – 1 x 1 1 1 … n-bit adder sn – 1 1 Add ¤ Sub control x 0 yn-1 cn y 0 s 1 y 0 c 0 s 0 [ Figure 3. 12 from the textbook ]

Subtraction: when control = 1 yn – 1 y 1 1 xn – 1 x 1 1 1 … n-bit adder sn – 1 1 Add ¤ Sub control x 0 yn-1 cn y 0 y 1 y 0 1 s 0 carry for the first column! [ Figure 3. 12 from the textbook ]

Examples of determination of overflow ( + 7) + ( + 2) 0111 + 0010 (– 7) + ( + 2) 1001 + 0010 ( + 9) 1001 c 4 = 0 c 3 = 1 (– 5) 1011 c 4 = 0 c 3 = 0 ( + 7) + ( – 2) 0111 + 1110 (– 7) + (– 2) 1001 + 1110 ( + 5) 10101 c 4 = 1 c 3 = 1 (– 9) 10 1 1 1 c 4 = 1 c 3 = 0 [ Figure 3. 13 from the textbook ]

Examples of determination of overflow ( + 7) + ( + 2) ( + 9) ( + 7) + ( – 2) ( + 5) 0111 + 0010 1001 c 4 = 0 c 3 = 1 Overflow (– 7) + ( + 2) 1001 + 0010 (– 5) 1011 c 4 = 0 c 3 = 0 occurs only in these 0 1 1 1 two cases. (– 7) + 1110 + (– 2) 10101 c 4 = 1 c 3 = 1 (– 9) 1001 + 1110 10 1 1 1 c 4 = 1 c 3 = 0 [ Figure 3. 13 from the textbook ]

Examples of determination of overflow ( + 7) + ( + 2) ( + 9) ( + 7) + ( – 2) ( + 5) 0111 + 0010 1001 c 4 = 0 c 3 = 1 Overflow (– 7) + ( + 2) 1001 + 0010 (– 5) 1011 c 4 = 0 c 3 = 0 occurs only in these 0 1 1 1 two cases. (– 7) + 1110 + (– 2) 10101 c 4 = 1 c 3 = 1 (– 9) 1001 + 1110 10 1 1 1 c 4 = 1 c 3 = 0 Overflow = c 3 c 4 + c 3 c 4 [ Figure 3. 13 from the textbook ]

Examples of determination of overflow ( + 7) + ( + 2) ( + 9) ( + 7) + ( – 2) ( + 5) 0111 + 0010 1001 c 4 = 0 c 3 = 1 Overflow (– 7) + ( + 2) 1001 + 0010 (– 5) 1011 c 4 = 0 c 3 = 0 occurs only in these 0 1 1 1 two cases. (– 7) + 1110 + (– 2) 10101 c 4 = 1 c 3 = 1 (– 9) 1001 + 1110 10 1 1 1 c 4 = 1 c 3 = 0 Overflow = c 3 c 4 + c 3 c 4 XOR [ Figure 3. 13 from the textbook ]

Calculating overflow for 4 -bit numbers with only three significant bits

Calculating overflow for n-bit numbers with only n-1 significant bits

Another way to look at the overflow issue

Another way to look at the overflow issue If both numbers that we are adding have the same sign but the sum does not, then we have an overflow.

Questions?

THE END