Cpr E 281 Digital Logic Instructor Alexander Stoytchev










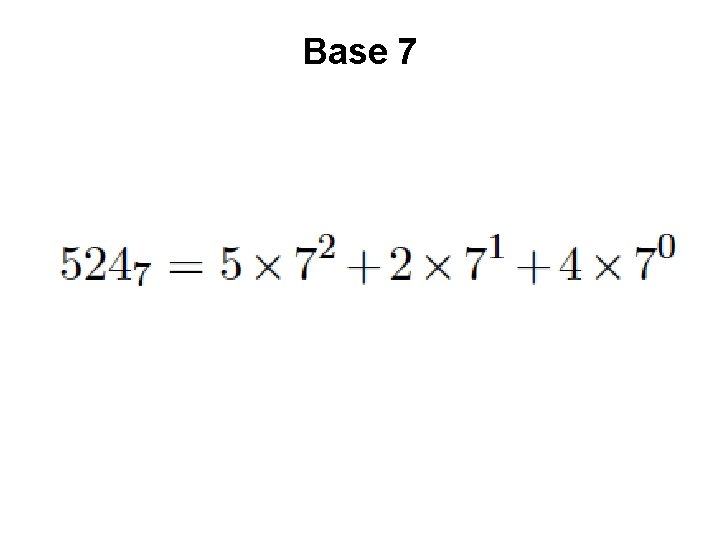
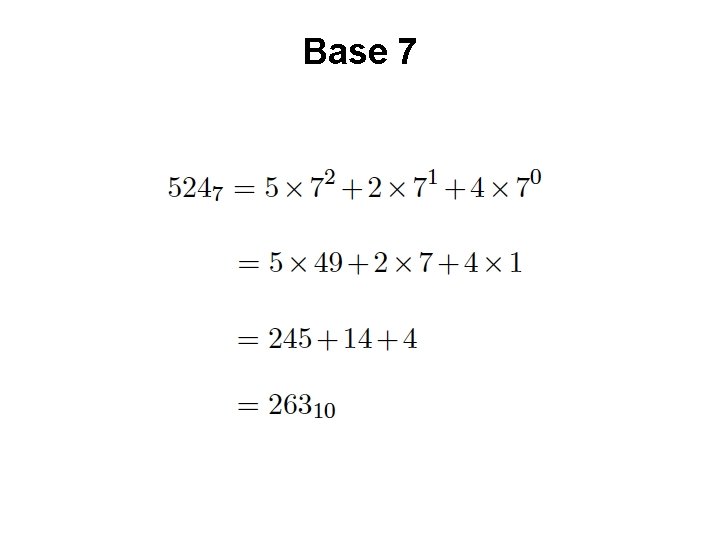













![Addition of two 1 -bit numbers [ Figure 2. 12 from the textbook ] Addition of two 1 -bit numbers [ Figure 2. 12 from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-38.jpg)






![The Half-Adder [ Figure 3. 1 c-d from the textbook ] The Half-Adder [ Figure 3. 1 c-d from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-62.jpg)

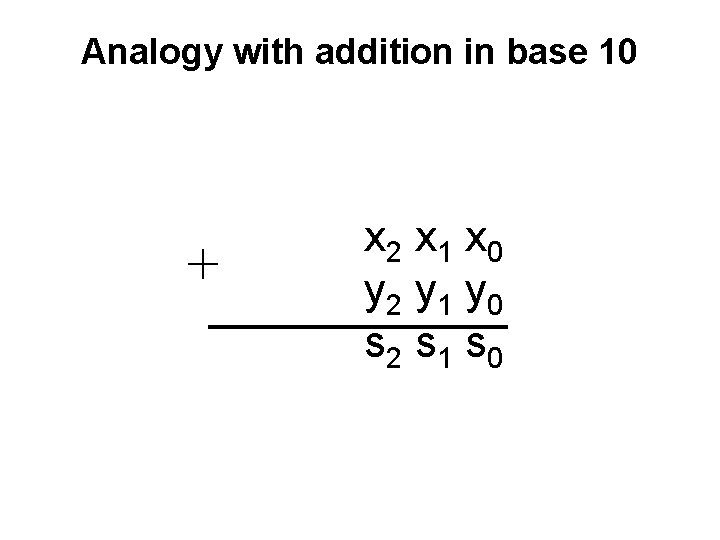
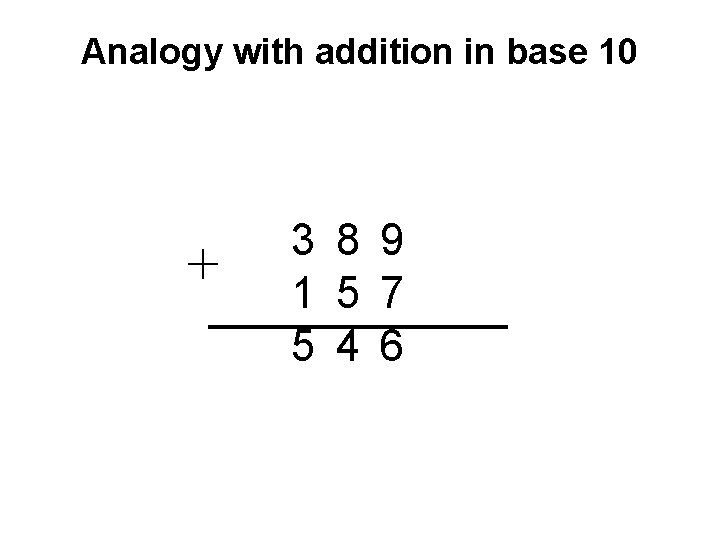



![Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ] Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-73.jpg)
![Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ] Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-74.jpg)
![Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ] Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-77.jpg)

![This is called the Full-Adder [ Figure 3. 3 c from the textbook ] This is called the Full-Adder [ Figure 3. 3 c from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-80.jpg)








![[ Figure 3. 6 a from the textbook ] [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-97.jpg)
![A A [ Figure 3. 6 a from the textbook ] A A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-98.jpg)
![A A 2 A [ Figure 3. 6 a from the textbook ] A A 2 A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-99.jpg)
![A 2 A A A [ Figure 3. 6 a from the textbook ] A 2 A A A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-100.jpg)






![[ Figure 3. 6 b from the textbook ] [ Figure 3. 6 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-108.jpg)

![2 A A 3 A [ Figure 3. 6 b from the textbook ] 2 A A 3 A [ Figure 3. 6 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-110.jpg)


- Slides: 112

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Addition of Unsigned Numbers Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • HW 4 is due today

Administrative Stuff • HW 5 is due next Monday

Administrative Stuff • The first midterm is this Friday

Quick Review

Number Systems

Number Systems n-th digit (most significant) 0 -th digit (least significant)

Number Systems base n-th digit (most significant) power 0 -th digit (least significant)

The Decimal System

The Decimal System

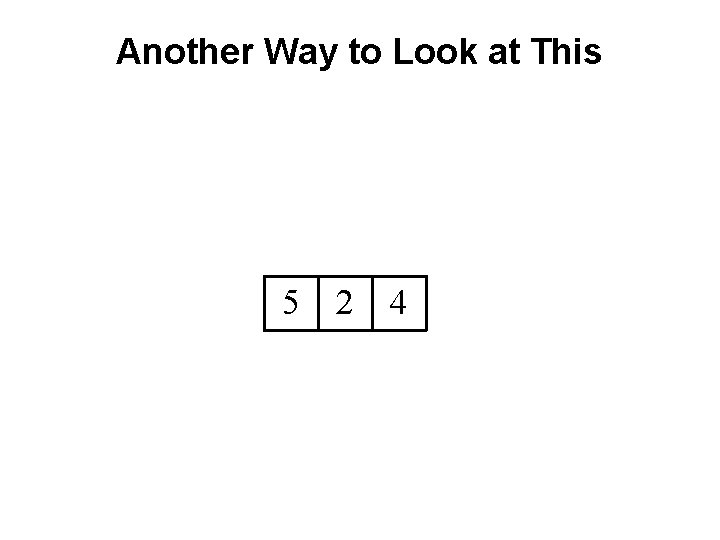
Another Way to Look at This 5 2 4

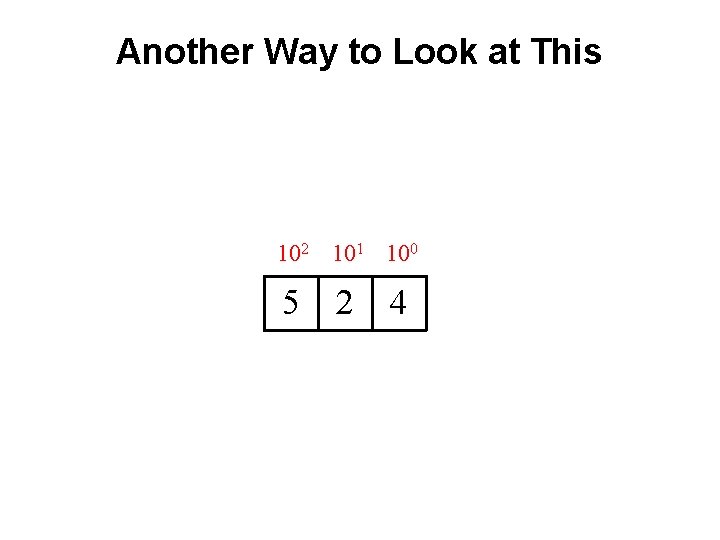
Another Way to Look at This 102 101 100 5 2 4

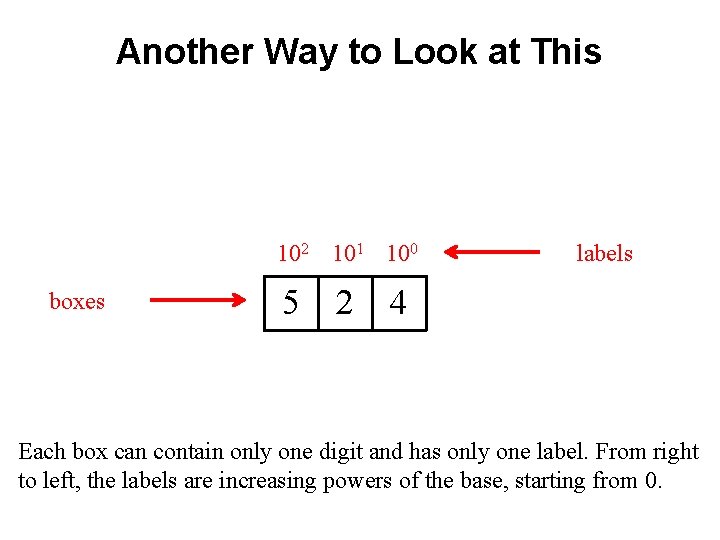
Another Way to Look at This 102 101 100 boxes 5 2 labels 4 Each box can contain only one digit and has only one label. From right to left, the labels are increasing powers of the base, starting from 0.
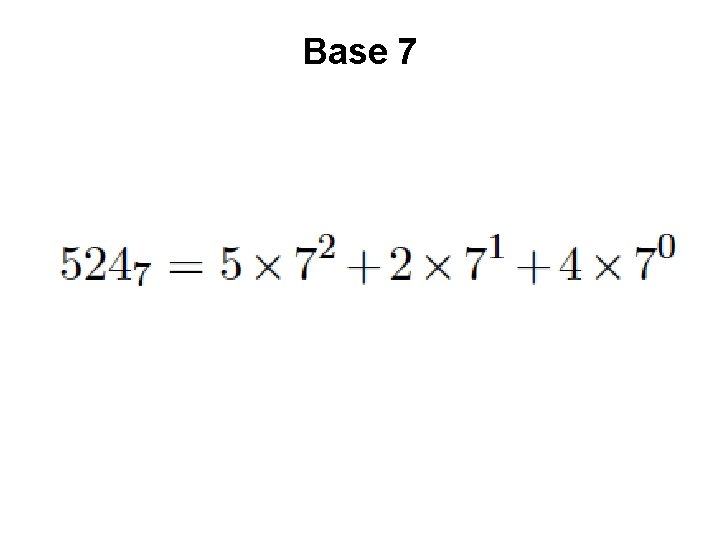
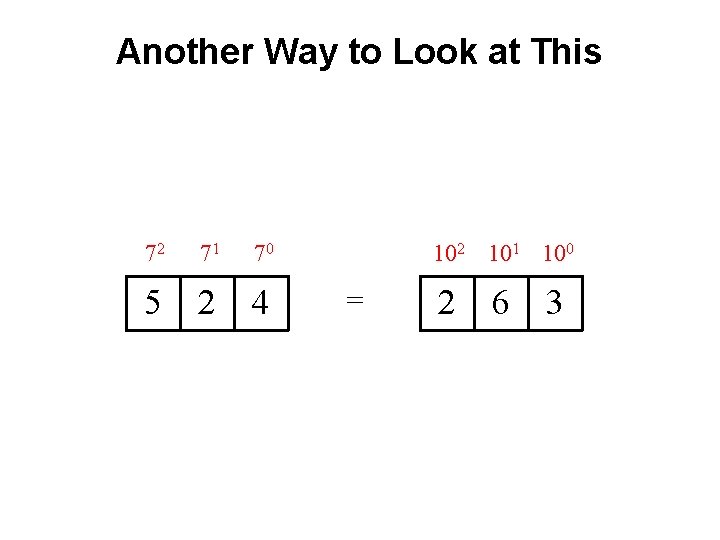
Base 7

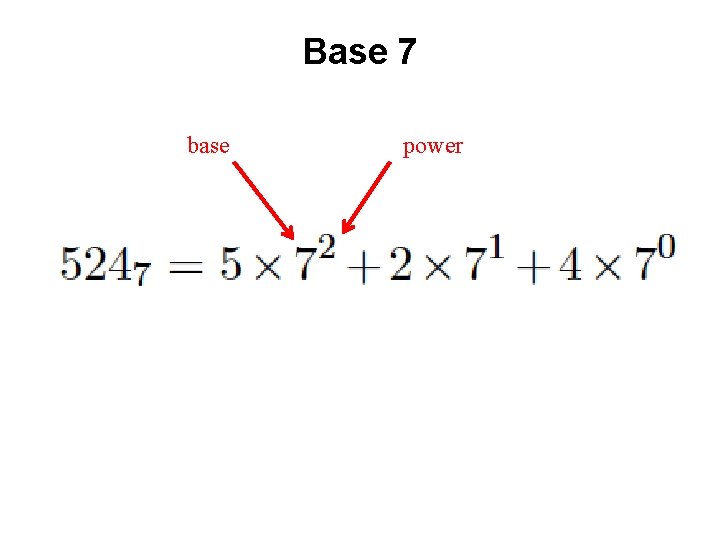
Base 7 base power

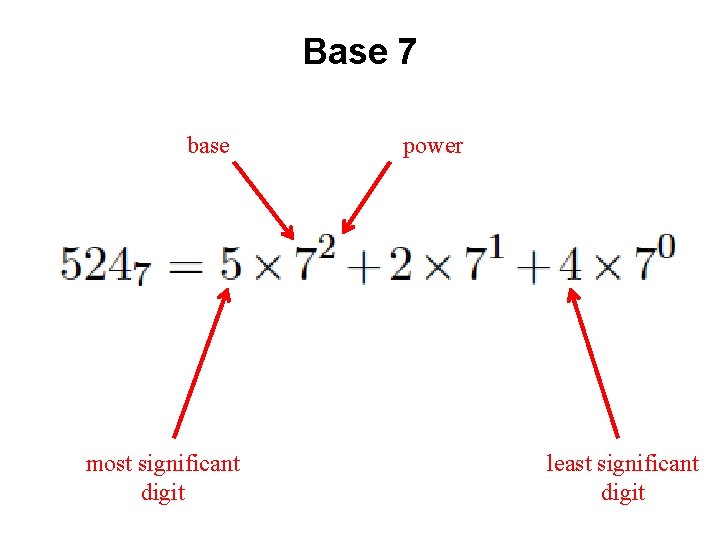
Base 7 base most significant digit power least significant digit
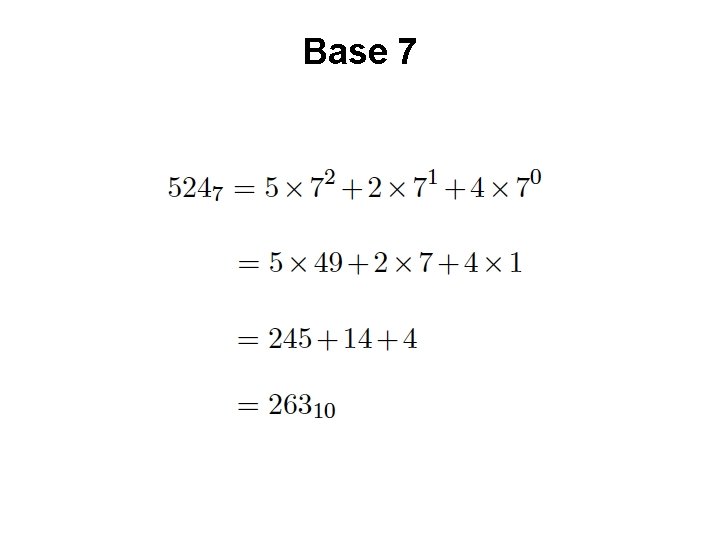
Base 7

Another Way to Look at This 72 71 70 5 2 4 102 101 100 = 2 6 3

Binary Numbers (Base 2)

Binary Numbers (Base 2) base most significant bit power least significant bit

Binary Numbers (Base 2)

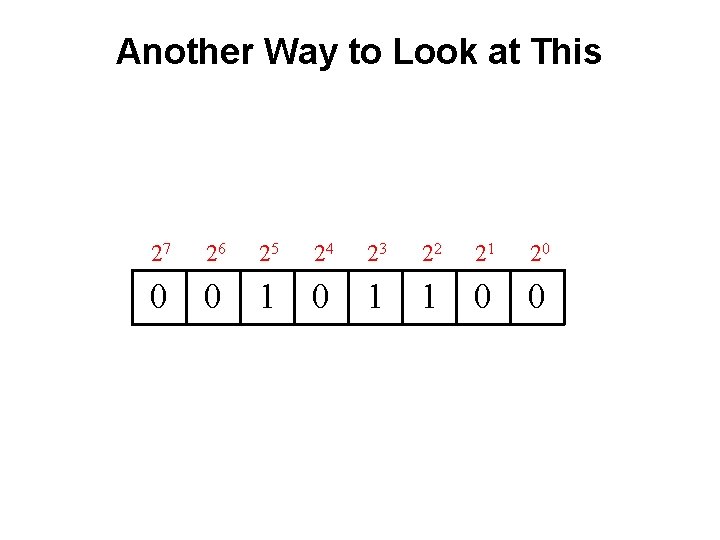
Another Example

Powers of 2

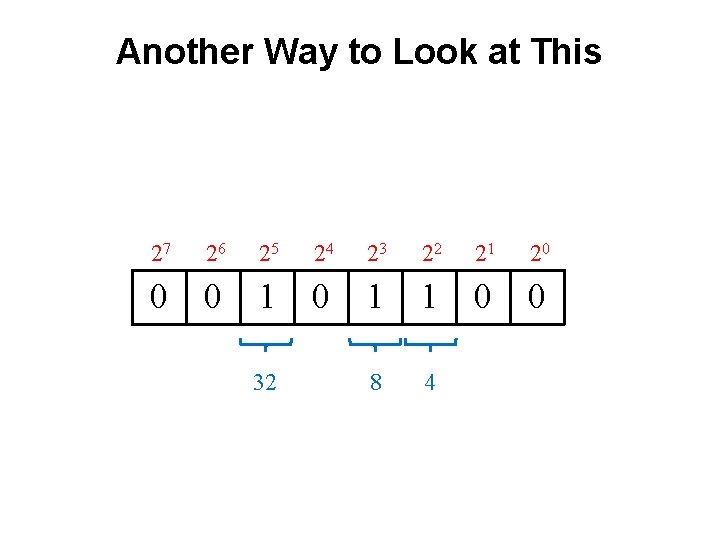
What is the value of this binary number? • 00101100 • 0 0 1 1 0 0 • 0*27 + 0*26 + 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 0*20 • 0*128 + 0*64 + 1*32 + 0*16 + 1*8 + 1*4 + 0*2 + 0*1 • 32+ 8 + 4 = 44 (in decimal)

Another Way to Look at This 27 26 25 24 23 22 21 20 0 0 1 1 0 0

Another Way to Look at This 27 26 25 24 23 22 21 20 0 0 1 1 0 0 8 4 32

Signed v. s. Unsigned Numbers

Two Different Types of Binary Numbers Unsigned numbers • All bits jointly represent a positive integer. • Negative numbers cannot be represented this way. Signed numbers • • The left-most bit represents the sign of the number. If that bit is 0, then the number is positive. If that bit is 1, then the number is negative. The magnitude of the largest number that can be represented in this way is twice smaller than the largest number in the unsigned representation.

Unsigned Representation 27 26 25 24 23 22 21 20 0 0 1 1 0 0 This represents + 44.

Unsigned Representation 27 26 25 24 23 22 21 20 1 0 1 1 0 0 This represents + 172.

Signed Representation (using the left-most bit as the sign) sign 26 25 24 23 22 21 20 0 0 1 1 0 0 This represents + 44.

Signed Representation (using the left-most bit as the sign) sign 26 25 24 23 22 21 20 1 0 1 1 0 0 This represents – 44.

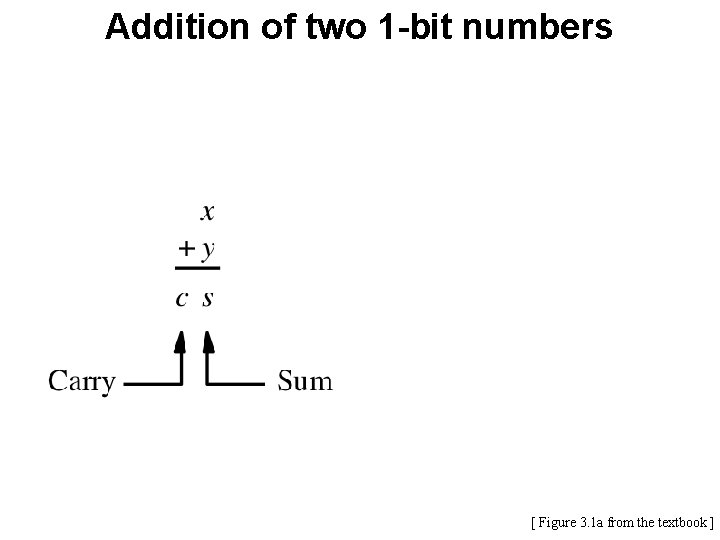
Today’s Lecture is About Addition of Unsigned Numbers

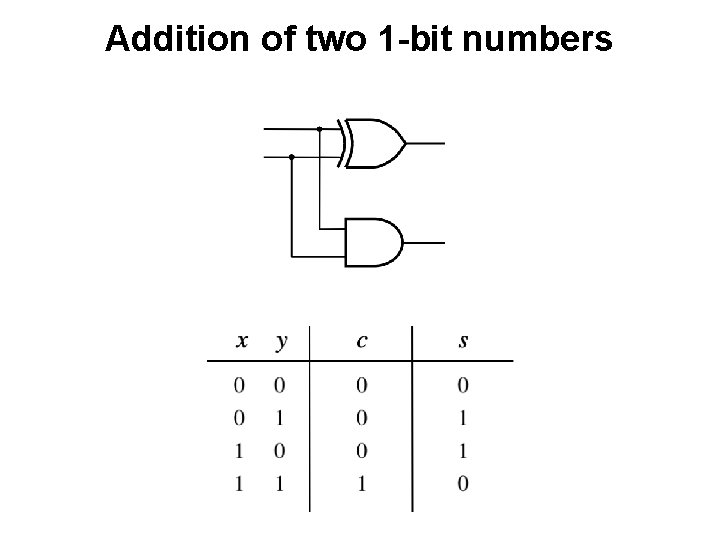
Addition of two 1 -bit numbers [ Figure 3. 1 a from the textbook ]

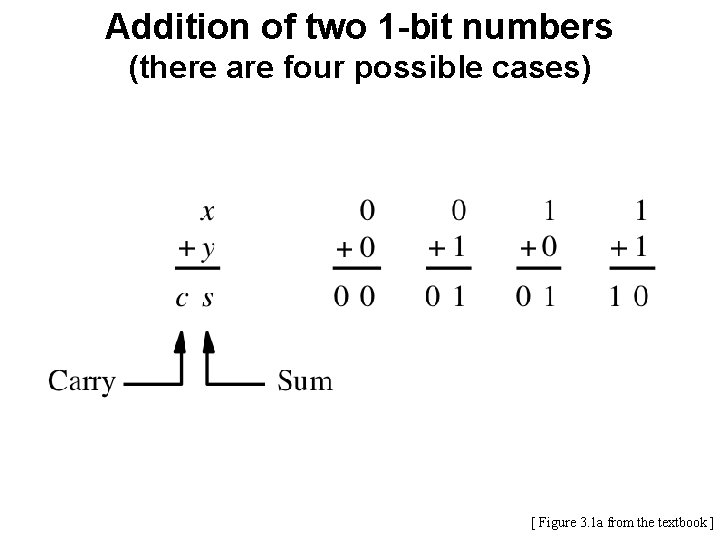
Addition of two 1 -bit numbers (there are four possible cases) [ Figure 3. 1 a from the textbook ]

Addition of two 1 -bit numbers (the truth table) [ Figure 3. 1 b from the textbook ]
![Addition of two 1 bit numbers Figure 2 12 from the textbook Addition of two 1 -bit numbers [ Figure 2. 12 from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-38.jpg)
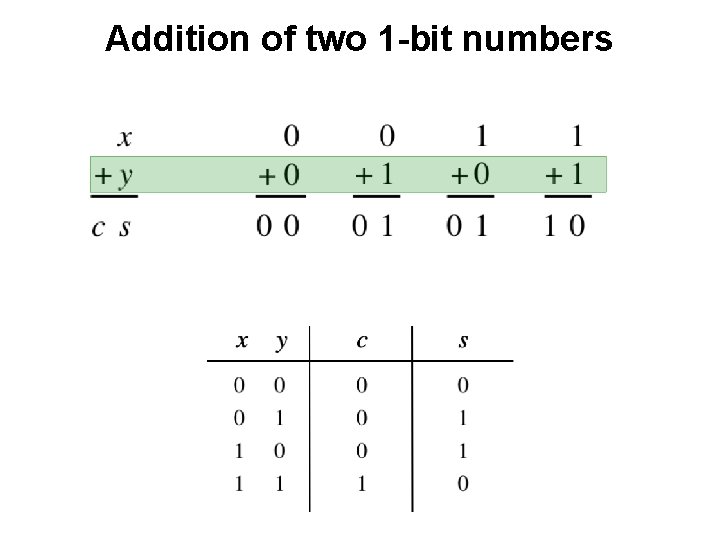
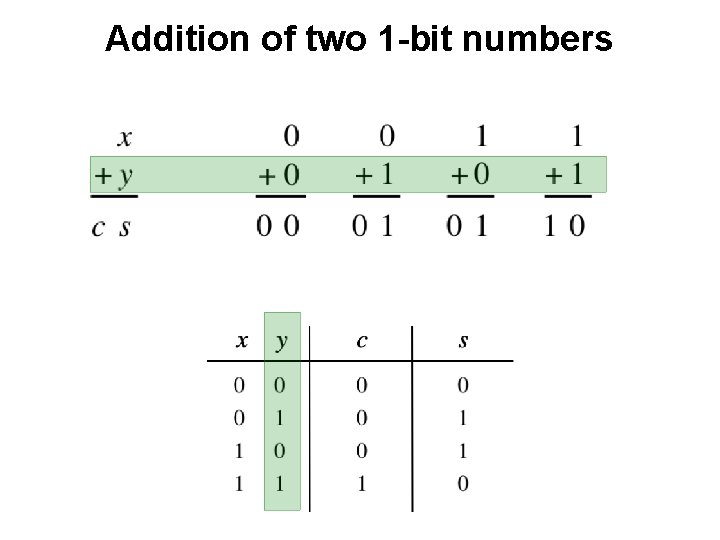
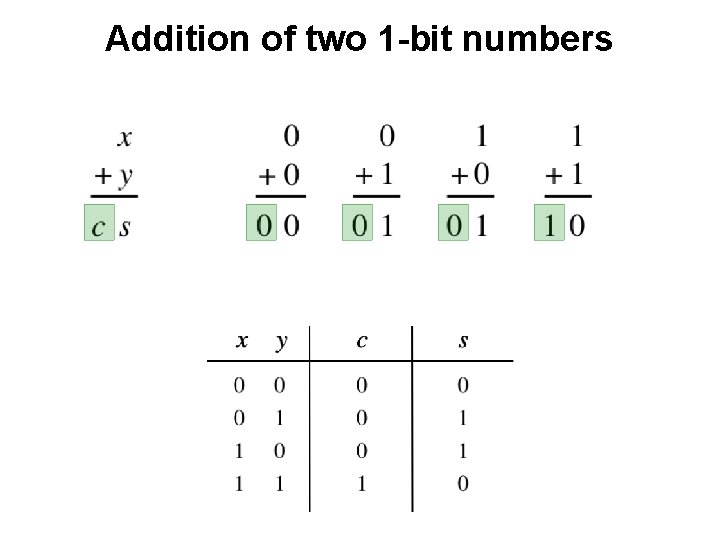
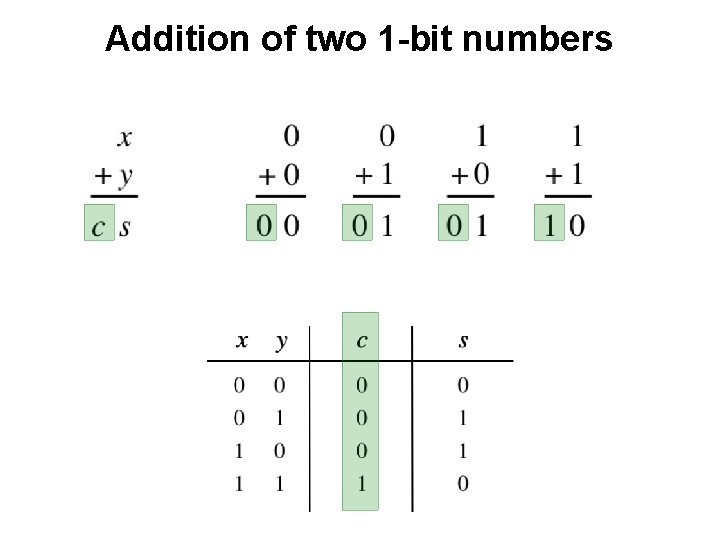
Addition of two 1 -bit numbers [ Figure 2. 12 from the textbook ]

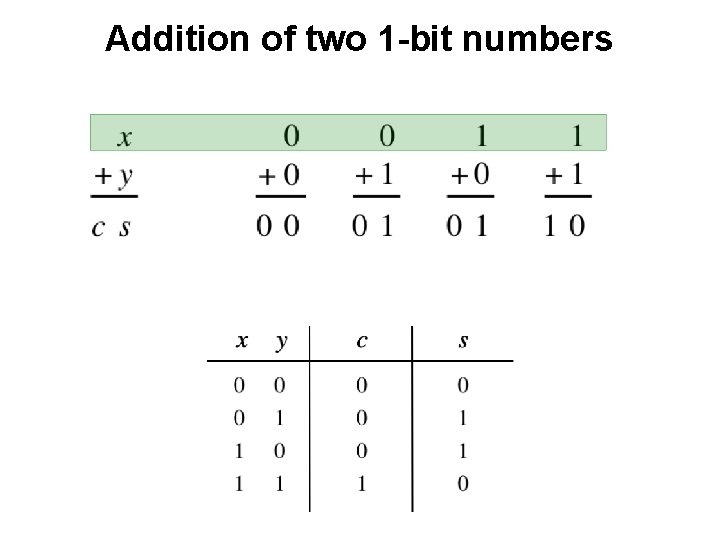
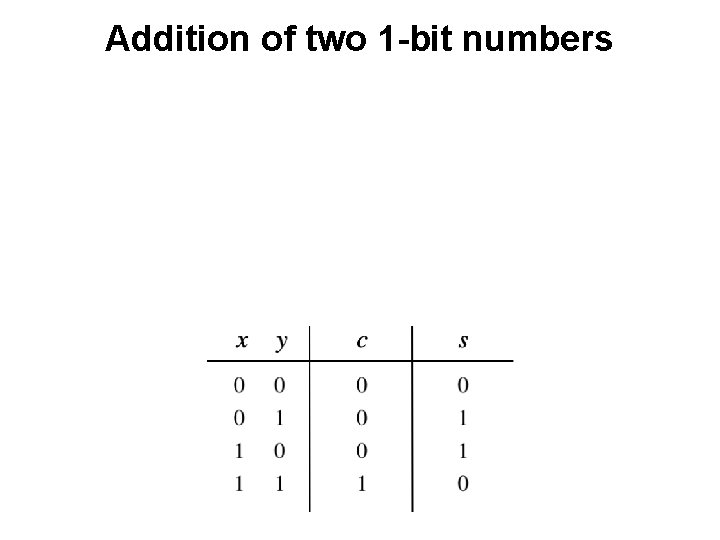
Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

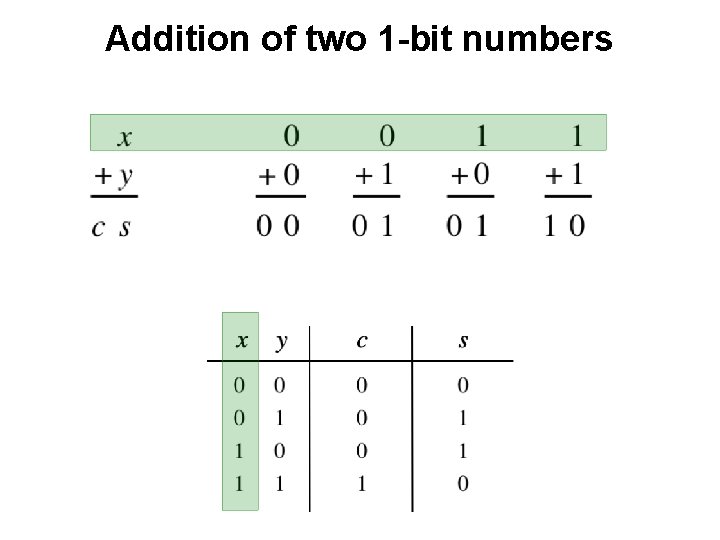
Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

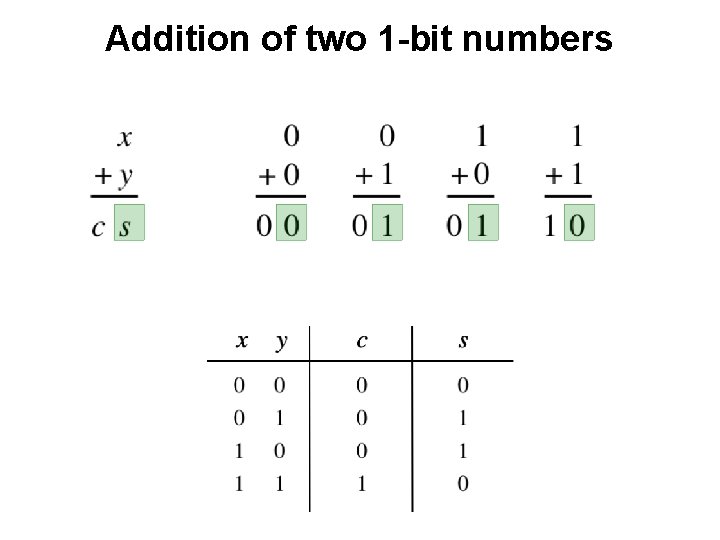
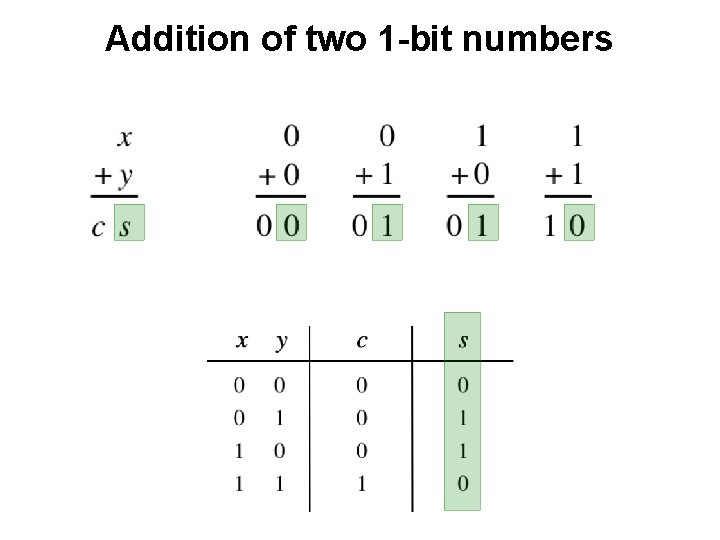
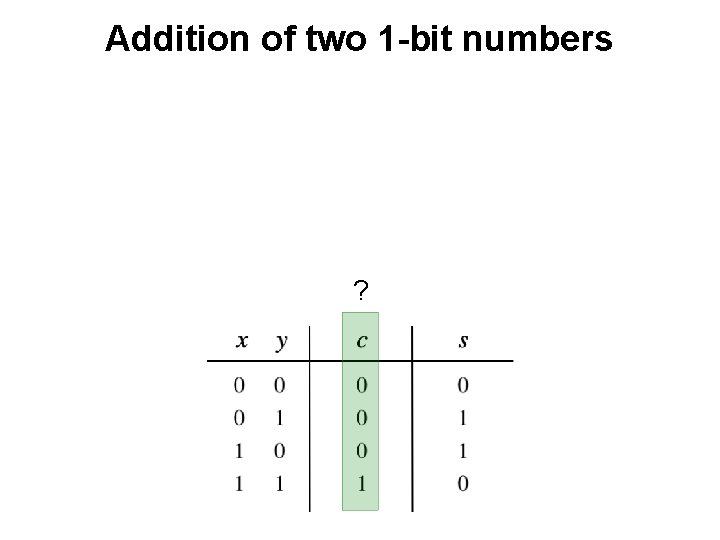
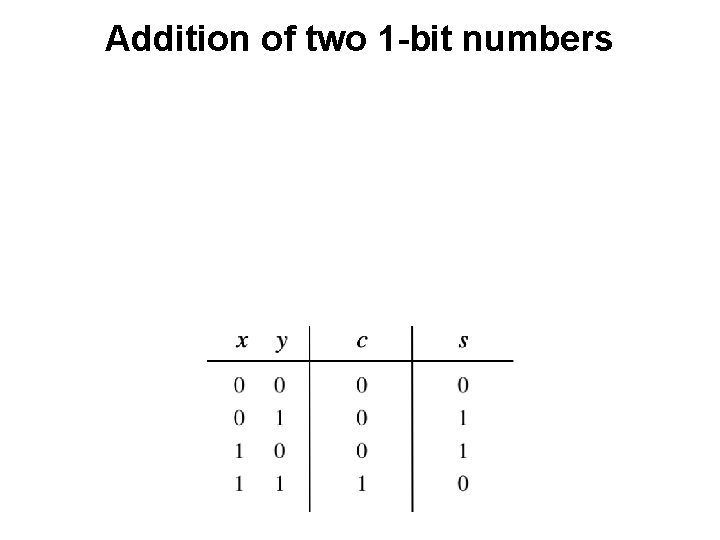
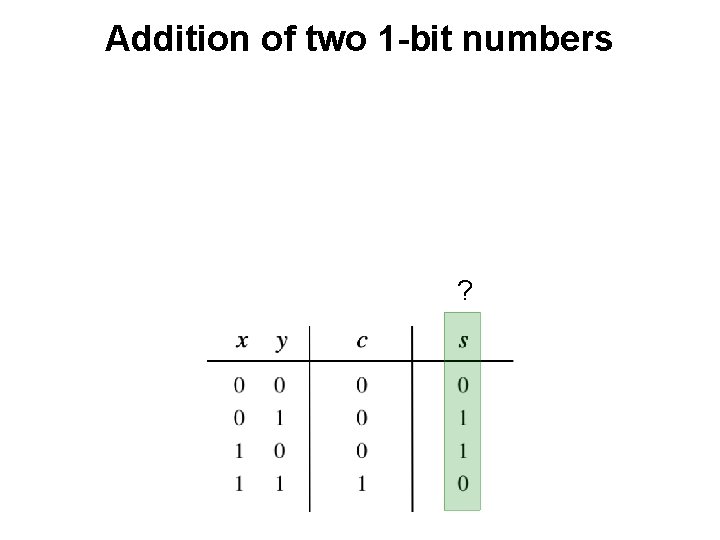
Addition of two 1 -bit numbers ?

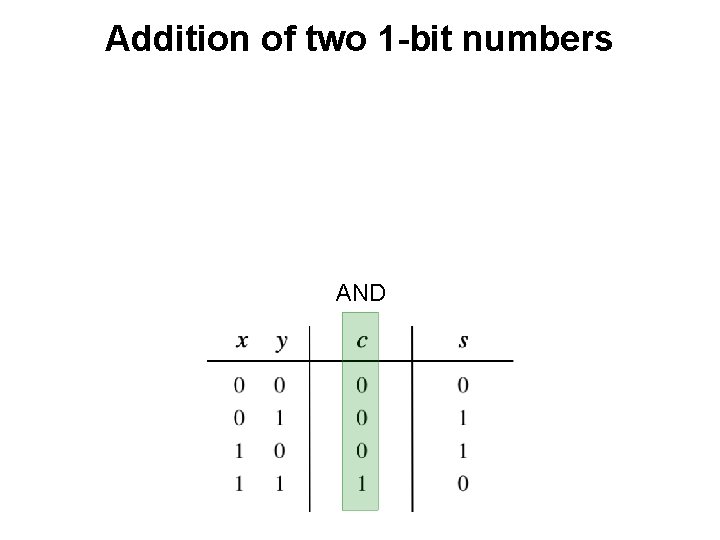
Addition of two 1 -bit numbers AND

Addition of two 1 -bit numbers

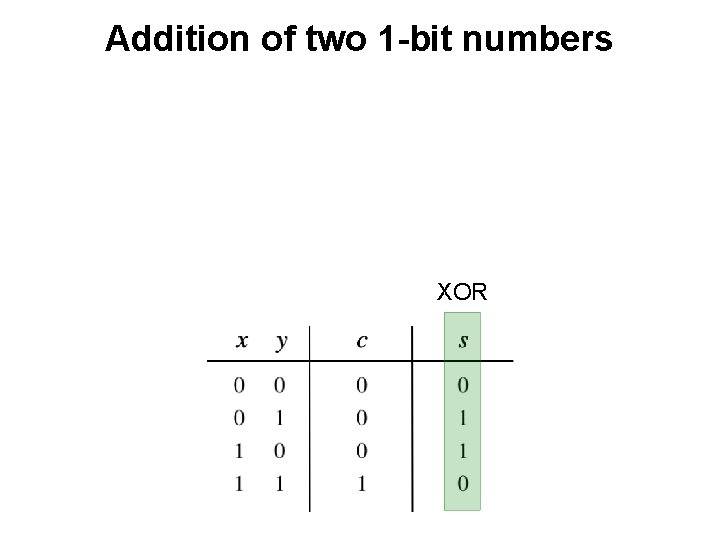
Addition of two 1 -bit numbers ?

Addition of two 1 -bit numbers XOR

Addition of two 1 -bit numbers

Addition of two 1 -bit numbers

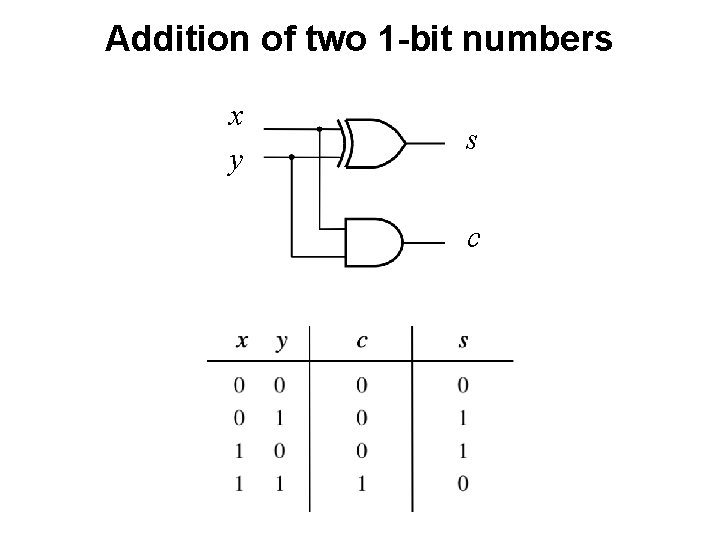
Addition of two 1 -bit numbers x y s c

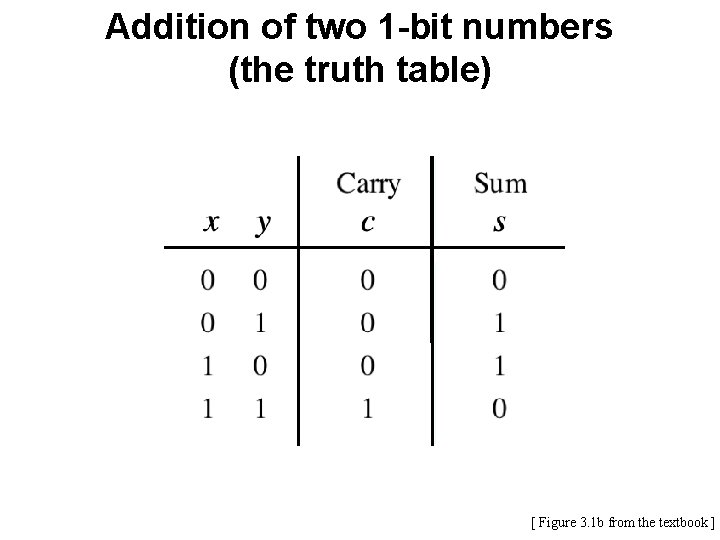
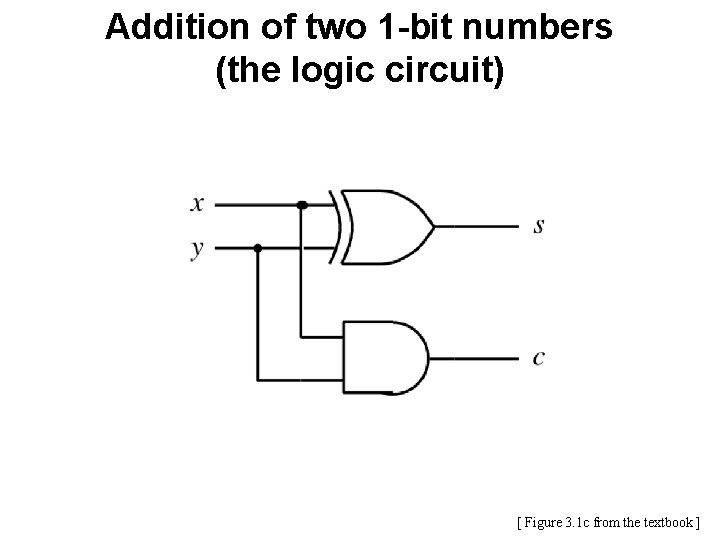
Addition of two 1 -bit numbers (the logic circuit) [ Figure 3. 1 c from the textbook ]
![The HalfAdder Figure 3 1 cd from the textbook The Half-Adder [ Figure 3. 1 c-d from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-62.jpg)
The Half-Adder [ Figure 3. 1 c-d from the textbook ]

Addition of Multibit Unsigned Numbers
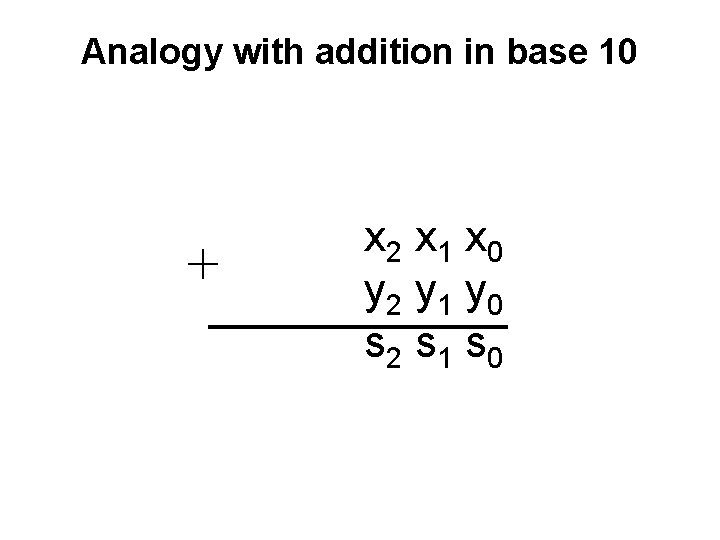
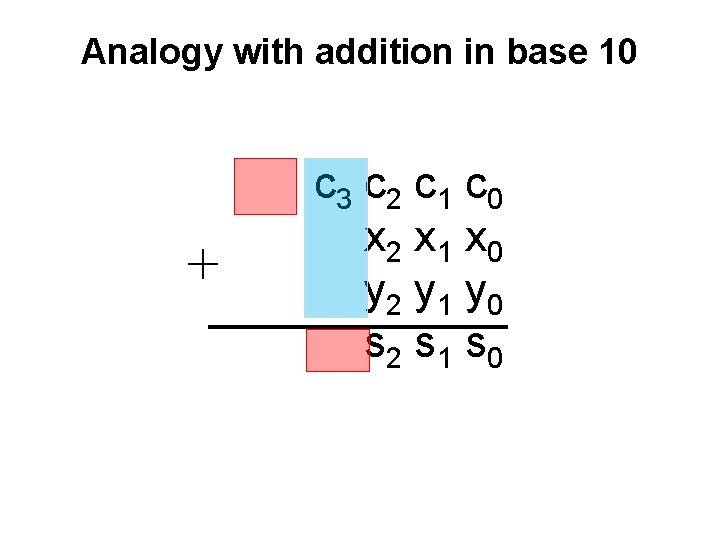
Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0
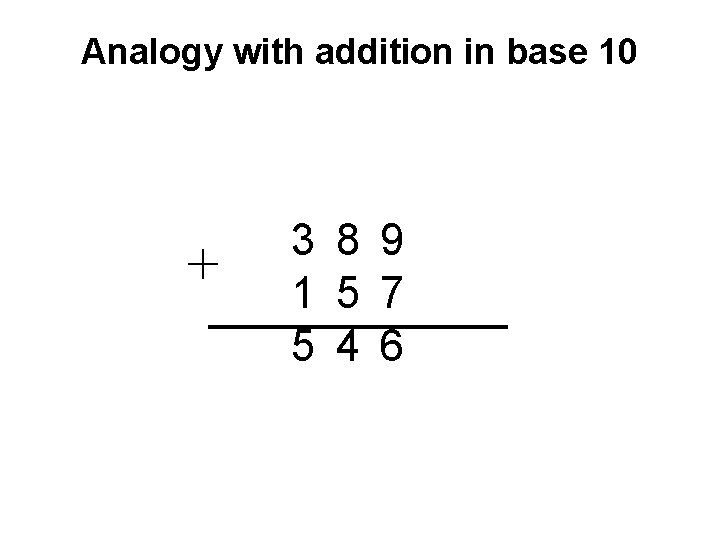
Analogy with addition in base 10 + 3 8 9 1 5 7 5 4 6

Analogy with addition in base 10 carry + 0 1 1 0 3 8 9 1 5 7 5 4 6

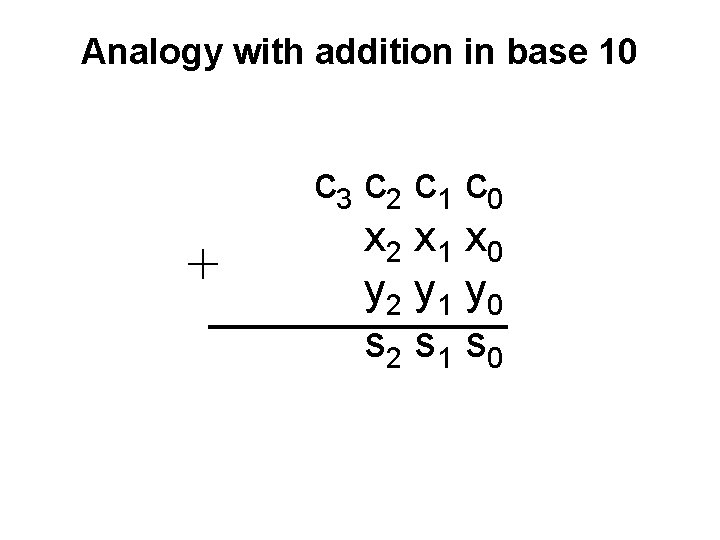
Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0

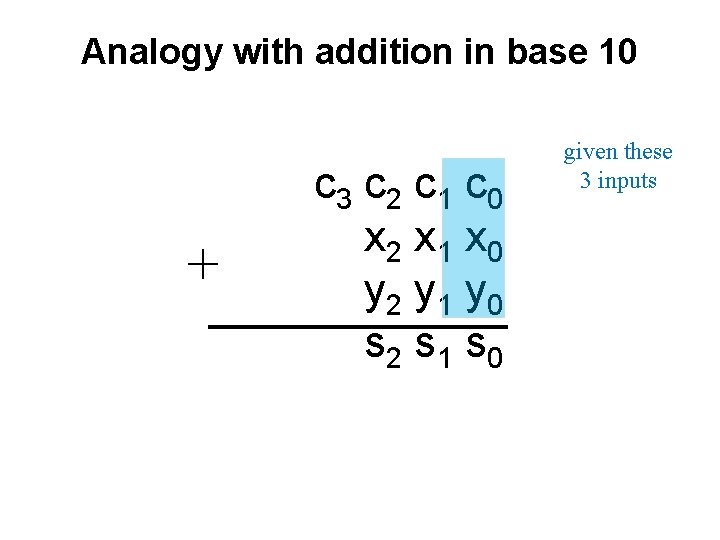
Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0 given these 3 inputs

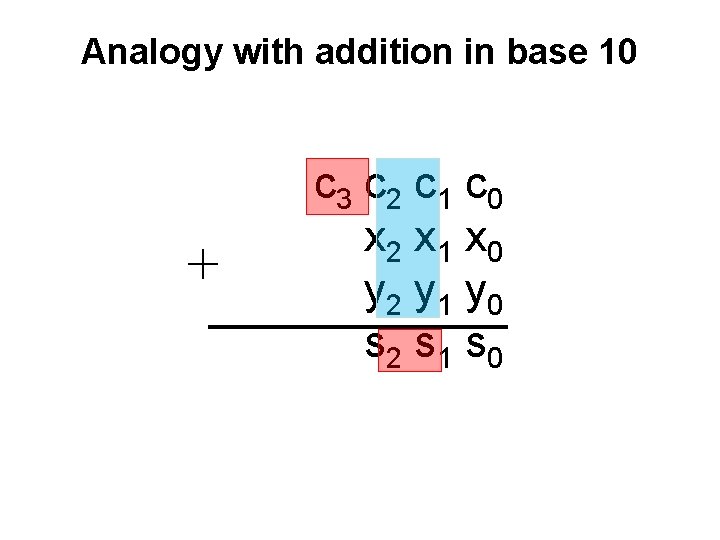
Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0 given these 3 inputs compute these 2 outputs

Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0

Analogy with addition in base 10 + c 3 c 2 c 1 c 0 x 2 x 1 x 0 y 2 y 1 y 0 s 2 s 1 s 0

Addition of multibit numbers Bit position i [ Figure 3. 2 from the textbook ]
![Problem Statement and Truth Table Figure 3 2 b from the textbook Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-73.jpg)
Problem Statement and Truth Table [ Figure 3. 2 b from the textbook ] [ Figure 3. 3 a from the textbook ]
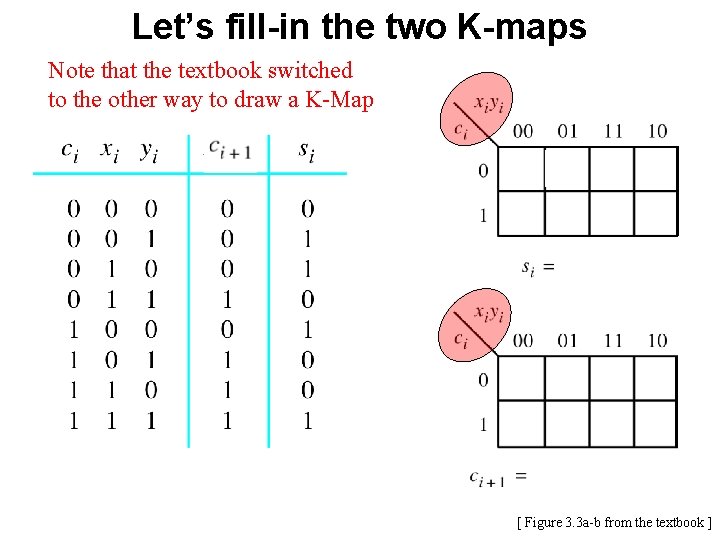
![Lets fillin the two Kmaps Figure 3 3 ab from the textbook Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-74.jpg)
Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps Note that the textbook switched to the other way to draw a K-Map [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps Note that the textbook switched to the other way to draw a K-Map [ Figure 3. 3 a-b from the textbook ]
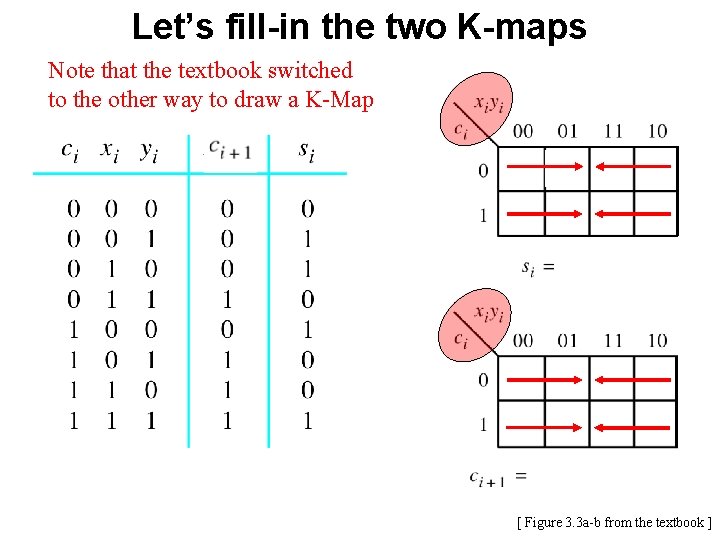
![Lets fillin the two Kmaps Figure 3 3 ab from the textbook Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-77.jpg)
Let’s fill-in the two K-maps [ Figure 3. 3 a-b from the textbook ]

Let’s fill-in the two K-maps 3 -input XOR [ Figure 3. 3 a-b from the textbook ]

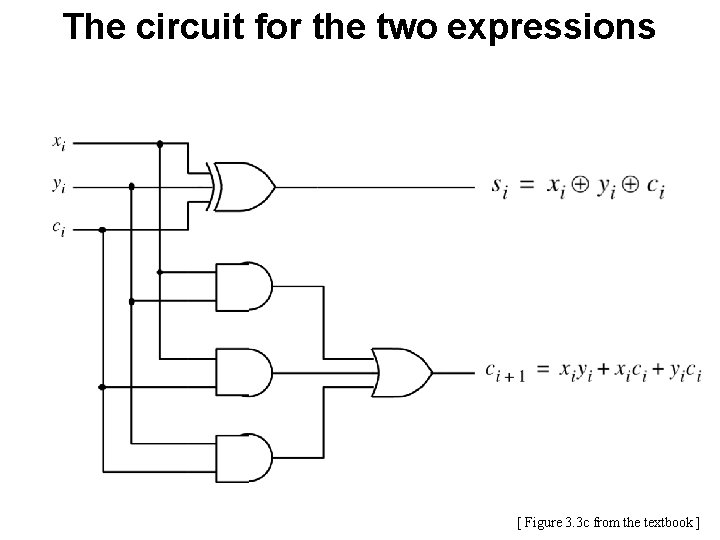
The circuit for the two expressions [ Figure 3. 3 c from the textbook ]
![This is called the FullAdder Figure 3 3 c from the textbook This is called the Full-Adder [ Figure 3. 3 c from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-80.jpg)
This is called the Full-Adder [ Figure 3. 3 c from the textbook ]

XOR Magic

XOR Magic

XOR Magic Can you prove this?

XOR Magic (si can be implemented in two different ways)

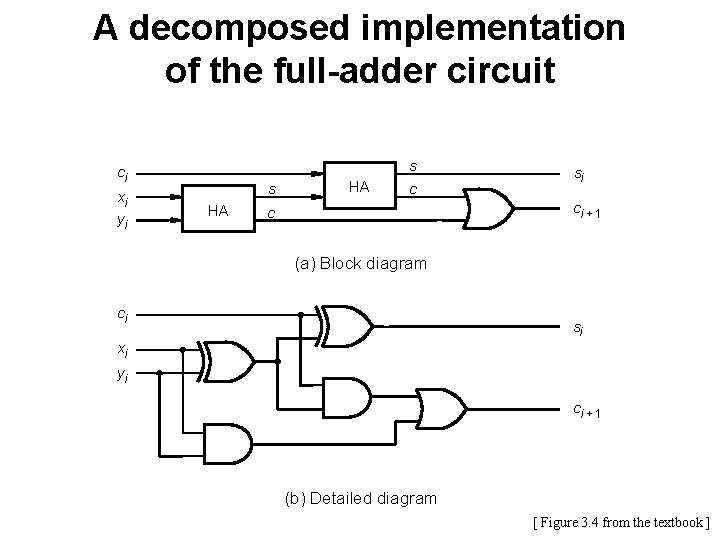
A decomposed implementation of the full-adder circuit s ci xi yi s HA HA c si ci + 1 c (a) Block diagram ci si xi yi ci + 1 (b) Detailed diagram [ Figure 3. 4 from the textbook ]

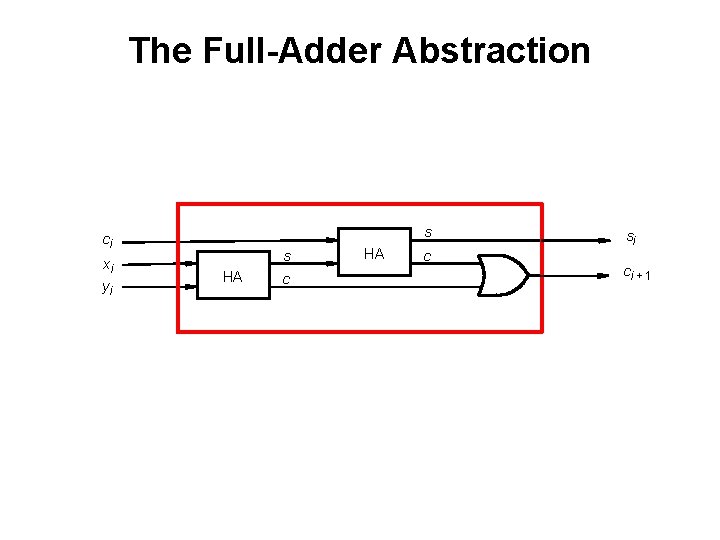
The Full-Adder Abstraction s ci xi yi s HA c si ci + 1

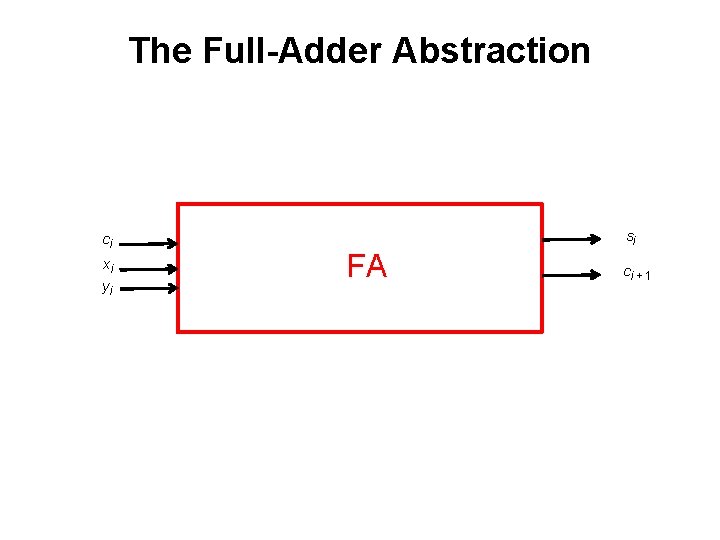
The Full-Adder Abstraction ci xi yi si FA ci + 1

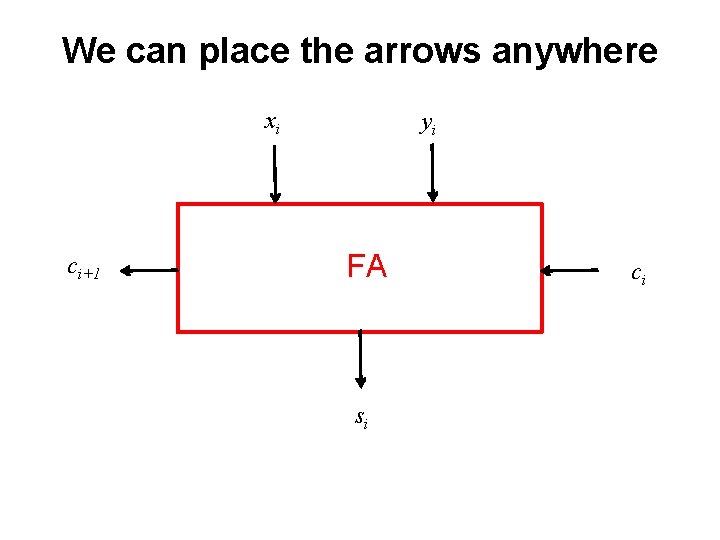
We can place the arrows anywhere xi ci+1 yi FA si ci

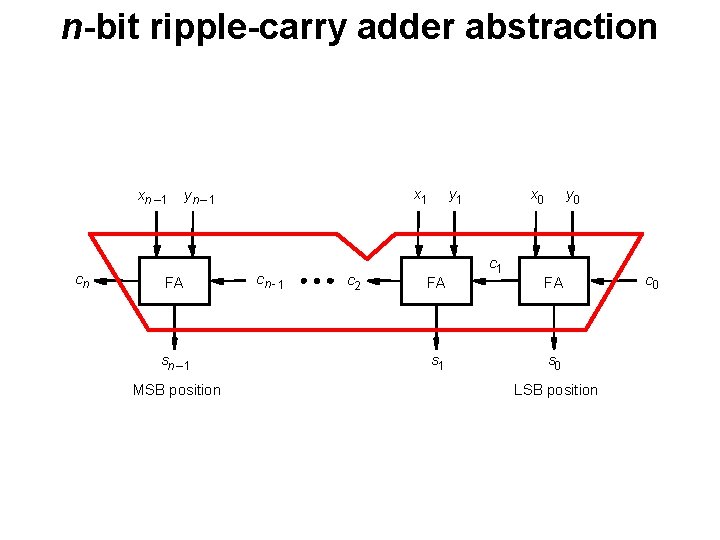
n-bit ripple-carry adder xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn - 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA c 0 s 0 LSB position [ Figure 3. 5 from the textbook ]

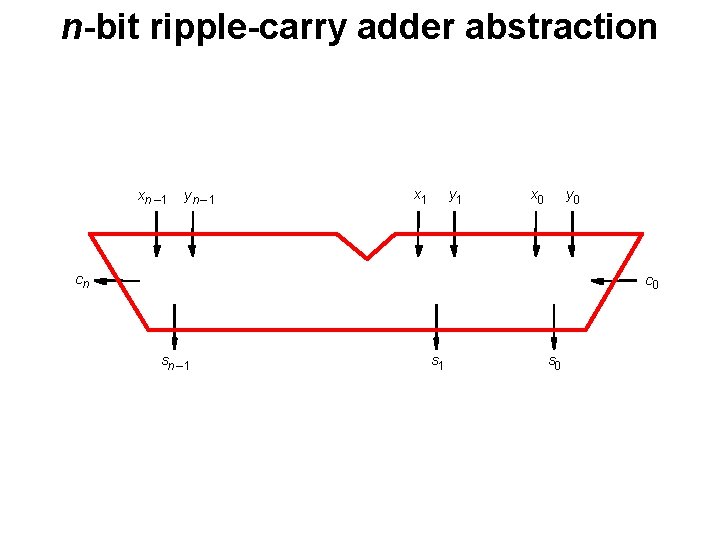
n-bit ripple-carry adder abstraction xn – 1 cn x 1 yn – 1 FA sn – 1 MSB position cn - 1 c 2 y 1 FA s 1 x 0 c 1 y 0 FA s 0 LSB position c 0

n-bit ripple-carry adder abstraction xn – 1 yn – 1 x 1 y 1 x 0 y 0 cn c 0 sn – 1 s 0

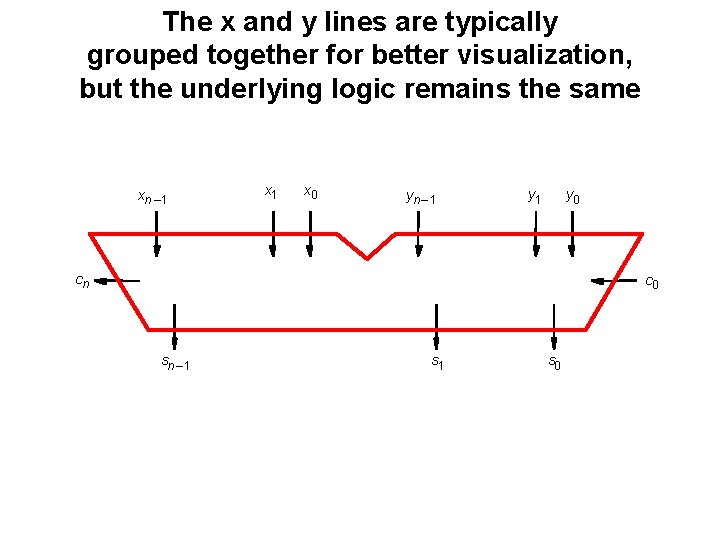
The x and y lines are typically grouped together for better visualization, but the underlying logic remains the same xn – 1 x 0 yn – 1 y 0 cn c 0 sn – 1 s 0

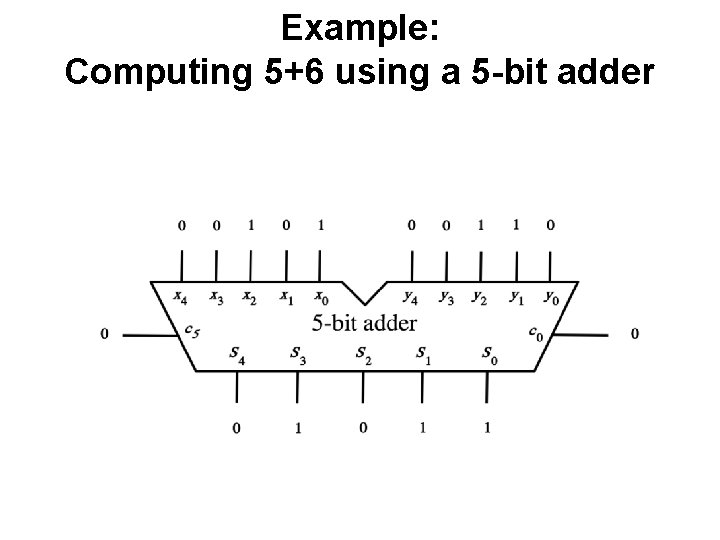
Example: Computing 5+6 using a 5 -bit adder

Example: Computing 5+6 using a 5 -bit adder 5 in decimal 6 in decimal 11 in decimal

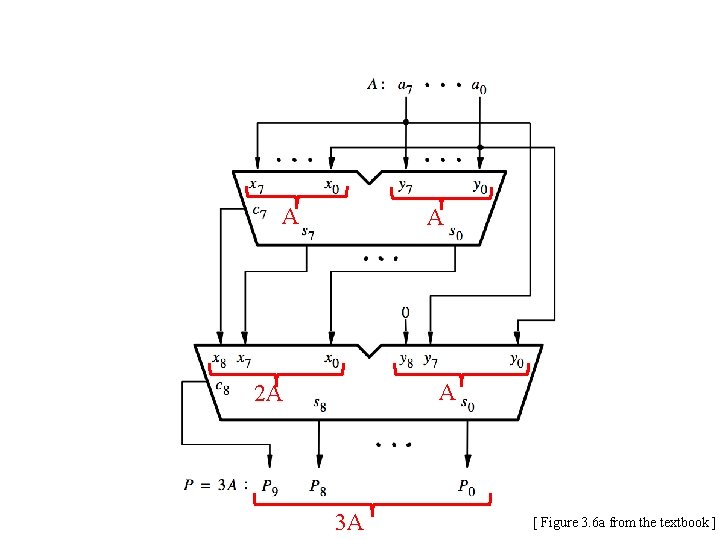
Design Example: Create a circuit that multiplies a number by 3

How to Get 3 A from A? • 3 A = A + A • 3 A = (A+A) + A • 3 A = 2 A +A
![Figure 3 6 a from the textbook [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-97.jpg)
[ Figure 3. 6 a from the textbook ]
![A A Figure 3 6 a from the textbook A A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-98.jpg)
A A [ Figure 3. 6 a from the textbook ]
![A A 2 A Figure 3 6 a from the textbook A A 2 A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-99.jpg)
A A 2 A [ Figure 3. 6 a from the textbook ]
![A 2 A A A Figure 3 6 a from the textbook A 2 A A A [ Figure 3. 6 a from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-100.jpg)
A 2 A A A [ Figure 3. 6 a from the textbook ]

A A A 2 A 3 A [ Figure 3. 6 a from the textbook ]

Decimal Multiplication by 10 What happens when we multiply a number by 10? 4 x 10 = ? 542 x 10 = ? 1245 x 10 = ?

Decimal Multiplication by 10 What happens when we multiply a number by 10? 4 x 10 = 40 542 x 10 = 5420 1245 x 10 = 12450

Decimal Multiplication by 10 What happens when we multiply a number by 10? 4 x 10 = 40 542 x 10 = 5420 1245 x 10 = 12450 You simply add a zero as the rightmost number

Binary Multiplication by 2 What happens when we multiply a number by 2? 011 times 2 = ? 101 times 2 = ? 110011 times 2 = ?

Binary Multiplication by 2 What happens when we multiply a number by 2? 011 times 2 = 0110 101 times 2 = 1010 110011 times 2 = 1100110

Binary Multiplication by 2 What happens when we multiply a number by 2? 011 times 2 = 0110 101 times 2 = 1010 110011 times 2 = 1100110 You simply add a zero as the rightmost number
![Figure 3 6 b from the textbook [ Figure 3. 6 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-108.jpg)
[ Figure 3. 6 b from the textbook ]

This is how we get 2 A [ Figure 3. 6 b from the textbook ]
![2 A A 3 A Figure 3 6 b from the textbook 2 A A 3 A [ Figure 3. 6 b from the textbook ]](https://slidetodoc.com/presentation_image_h2/696e13dafe21fbc38209b07c43ab443d/image-110.jpg)
2 A A 3 A [ Figure 3. 6 b from the textbook ]

Questions?

THE END
 Stoytchev 281
Stoytchev 281 Stoytchev 281
Stoytchev 281 Cpr e 281
Cpr e 281 Stoytchev
Stoytchev What is this
What is this Ipx-281
Ipx-281 Cs281 wordpress
Cs281 wordpress It is a circular or elliptical anticlinal structure
It is a circular or elliptical anticlinal structure Formation of soil
Formation of soil Itslearningccisd
Itslearningccisd Cs 281
Cs 281 Numeros romanos del 400 al 600
Numeros romanos del 400 al 600 18 gelecek aylara ait giderler ve gelir tahakkukları
18 gelecek aylara ait giderler ve gelir tahakkukları Dönem ayirici hesaplar 180 181 280 281 380 381
Dönem ayirici hesaplar 180 181 280 281 380 381 First order logic vs propositional logic
First order logic vs propositional logic First order logic vs propositional logic
First order logic vs propositional logic First order logic vs propositional logic
First order logic vs propositional logic Concurrent vs sequential
Concurrent vs sequential Cryptarithmetic problem logic+logic=prolog
Cryptarithmetic problem logic+logic=prolog 캠블리 단점
캠블리 단점 Majority circuit
Majority circuit Combinational logic sequential logic 차이
Combinational logic sequential logic 차이 Logic chapter three
Logic chapter three Digital logic design tutorial
Digital logic design tutorial Lock logic
Lock logic Timing diagram digital logic
Timing diagram digital logic Digital system design
Digital system design Digital logic controller
Digital logic controller Canonical form digital logic
Canonical form digital logic Digital logic design practice problems
Digital logic design practice problems Digital logic identities
Digital logic identities Digital logic design lectures
Digital logic design lectures Digital logic structures
Digital logic structures Consensus digital logic
Consensus digital logic Bubble matching digital logic
Bubble matching digital logic Digital logic and computer architecture
Digital logic and computer architecture Uncommon logic digital
Uncommon logic digital Digital design review
Digital design review Duality in discrete mathematics
Duality in discrete mathematics Digital logic design
Digital logic design Bubble matching digital logic
Bubble matching digital logic Participante silencioso
Participante silencioso Basic instructor course texas
Basic instructor course texas Basic instructor course texas
Basic instructor course texas Basic instructor course #1014
Basic instructor course #1014 Pepperball launcher nomenclature
Pepperball launcher nomenclature Neither of my two suitcases is adequate for this trip
Neither of my two suitcases is adequate for this trip Instructor vs teacher
Instructor vs teacher Cisco certified trainer
Cisco certified trainer Mptc firearms
Mptc firearms Basic instructor course texas
Basic instructor course texas Basic instructor course texas
Basic instructor course texas The virtual instructor
The virtual instructor Nfpa 1403
Nfpa 1403 Tp 12863
Tp 12863 Instructor operating station
Instructor operating station Catia instructor
Catia instructor Instructor
Instructor Ac61-98 plan of action
Ac61-98 plan of action Tcole 1014 basic instructor course
Tcole 1014 basic instructor course Usmc jrotc vacancies
Usmc jrotc vacancies How to become an nrp instructor mentor
How to become an nrp instructor mentor Cisco instructor certification
Cisco instructor certification Cbrf registry wi
Cbrf registry wi Nra certified instructor logo
Nra certified instructor logo Naismith was an instructor of
Naismith was an instructor of Please clean your own room
Please clean your own room Tcole advanced instructor course
Tcole advanced instructor course Tcole advanced instructor course
Tcole advanced instructor course Jrotc marksmanship instructor course online
Jrotc marksmanship instructor course online Optical illusion
Optical illusion Cyan medical terminology
Cyan medical terminology Basic instructor course #1014
Basic instructor course #1014 Basic instructor course tcole
Basic instructor course tcole Delmar cengage learning instructor resources
Delmar cengage learning instructor resources Instructor office hours
Instructor office hours Extracorporeal cpr
Extracorporeal cpr Definasi pertolongan cemas
Definasi pertolongan cemas Perbedaan cpr dan mpr
Perbedaan cpr dan mpr Basic life support
Basic life support Objective of cpr
Objective of cpr Cpr objectives
Cpr objectives What is the secondary survey in first aid
What is the secondary survey in first aid Llf in cpr
Llf in cpr Ems safety cpr
Ems safety cpr Emotional cpr training
Emotional cpr training Cpr hand placement sternum
Cpr hand placement sternum Cpr for beginners
Cpr for beginners American heart association recommends child cpr for:
American heart association recommends child cpr for: Pulse check in child cpr
Pulse check in child cpr Cab cpr meaning
Cab cpr meaning Dyrektywa cpr
Dyrektywa cpr Cpr in physical education
Cpr in physical education Cpr compression rate
Cpr compression rate When to stop cpr
When to stop cpr Do not start cpr in the following situations:
Do not start cpr in the following situations: Pulseless electrical activity
Pulseless electrical activity Cpr bydgoszcz
Cpr bydgoszcz Introduction for cpr
Introduction for cpr Cpr adrenaline dose
Cpr adrenaline dose Cpr in schools training kit
Cpr in schools training kit The 4 rs of cpr
The 4 rs of cpr Bantu mula krs
Bantu mula krs Resuscitation cpr
Resuscitation cpr Cpr vocabulary
Cpr vocabulary What is high quality cpr
What is high quality cpr Cpr for beginners
Cpr for beginners 4 r's of cpr
4 r's of cpr What does cabd stand for in cpr
What does cabd stand for in cpr What does cabd stand for in cpr
What does cabd stand for in cpr Cpr
Cpr Principles of cpr
Principles of cpr Titik tumpu cpr
Titik tumpu cpr




































































































































