Cpr E 281 Digital Logic Instructor Alexander Stoytchev

Cpr. E 281: Digital Logic Instructor: Alexander Stoytchev http: //www. ece. iastate. edu/~alexs/classes/

Intro to Verilog Cpr. E 281: Digital Logic Iowa State University, Ames, IA Copyright © Alexander Stoytchev

Administrative Stuff • HW 3 is due on Monday Sep 7 @ 4 p

Administrative Stuff • Sample homework solutions are posted on Canvas • Look under ‘Files’

Quick Review

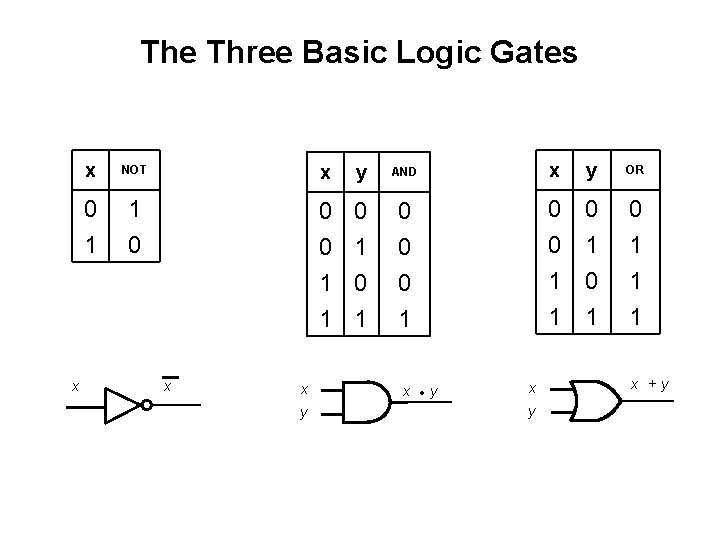
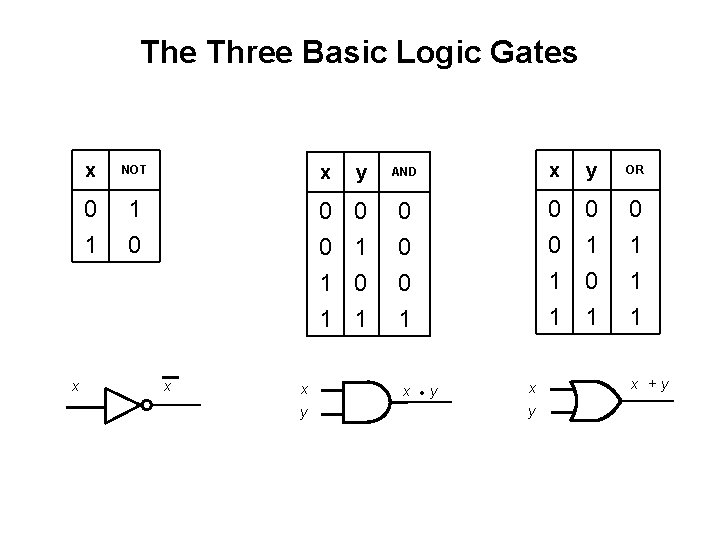
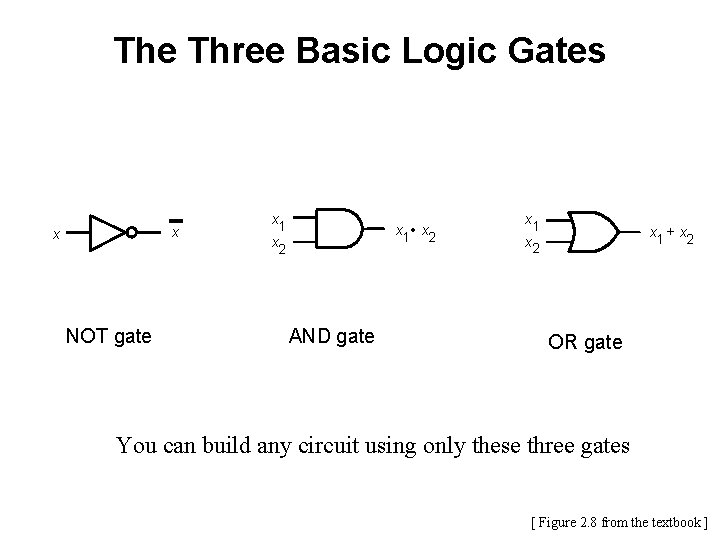
The Three Basic Logic Gates x x NOT x y AND x y OR 0 1 1 0 0 0 1 1 0 1 0 1 1 1 x x y x • y x +y

AND with Switches

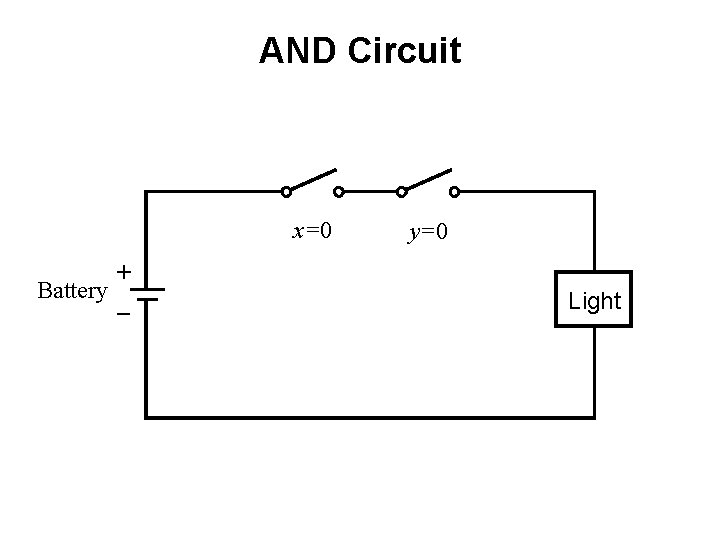
AND Circuit x=0 + Battery _ y=0 Light

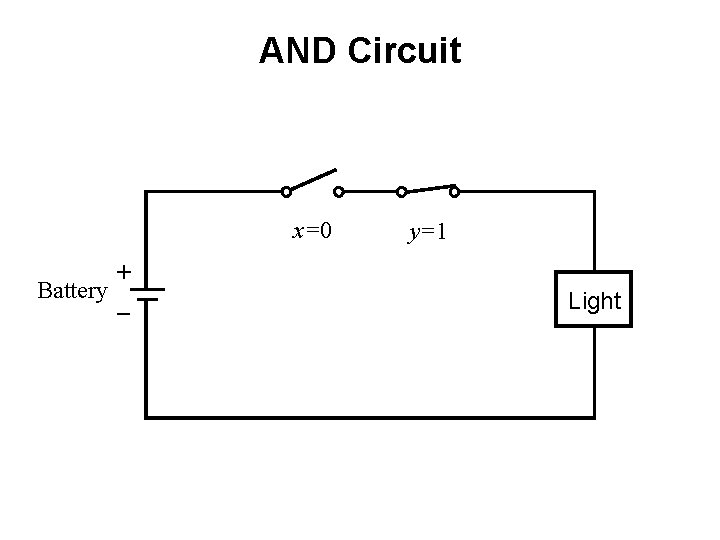
AND Circuit x=0 + Battery _ y=1 Light

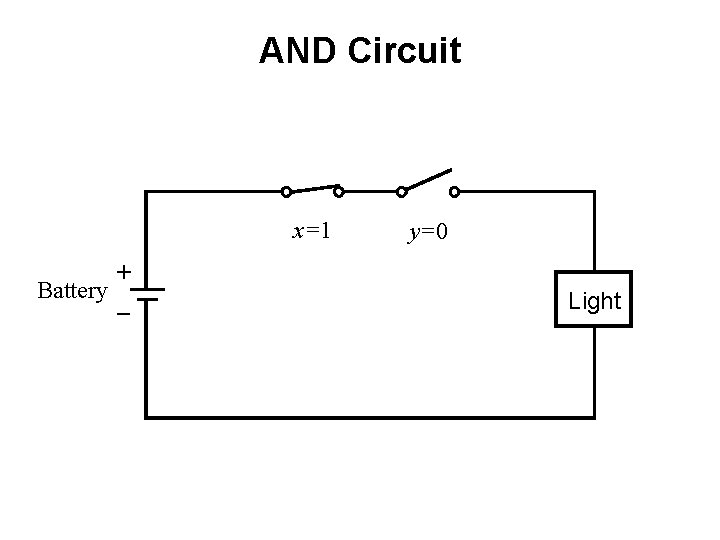
AND Circuit x=1 + Battery _ y=0 Light

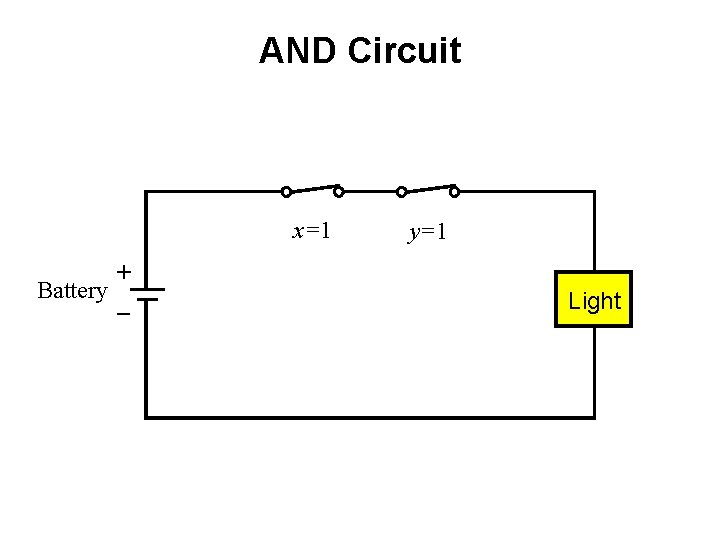
AND Circuit x=1 + Battery _ y=1 Light

NOT with Switches

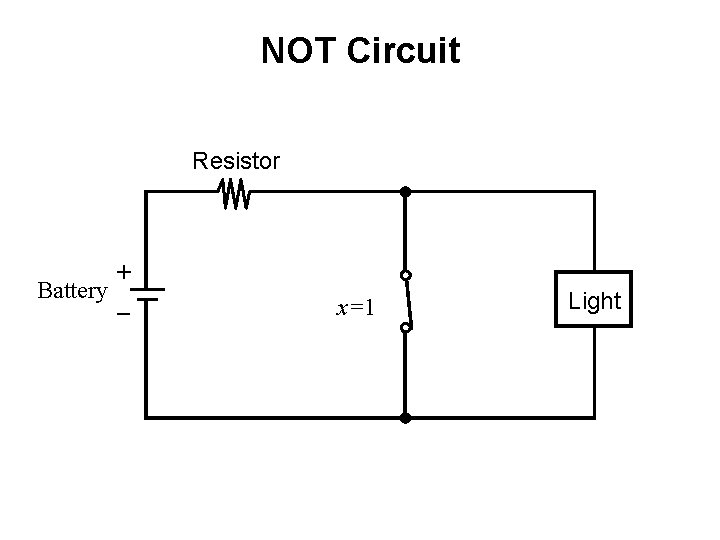
NOT Circuit Resistor + Battery _ x=1 Light

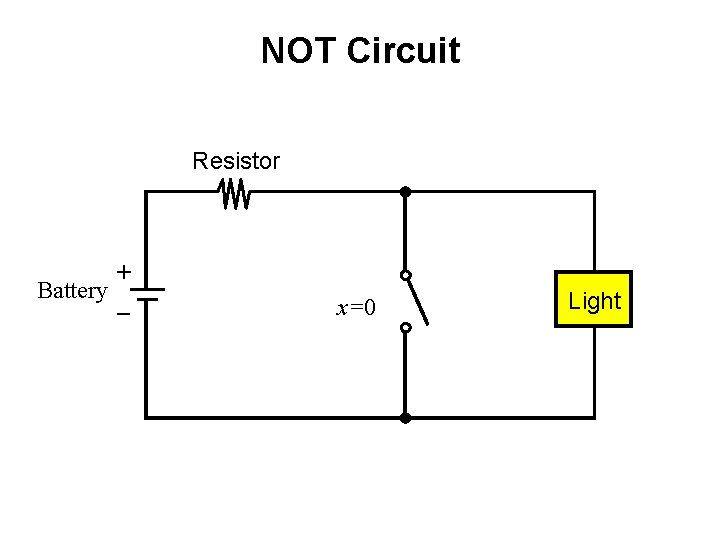
NOT Circuit Resistor + Battery _ x=0 Light

NAND with Switches

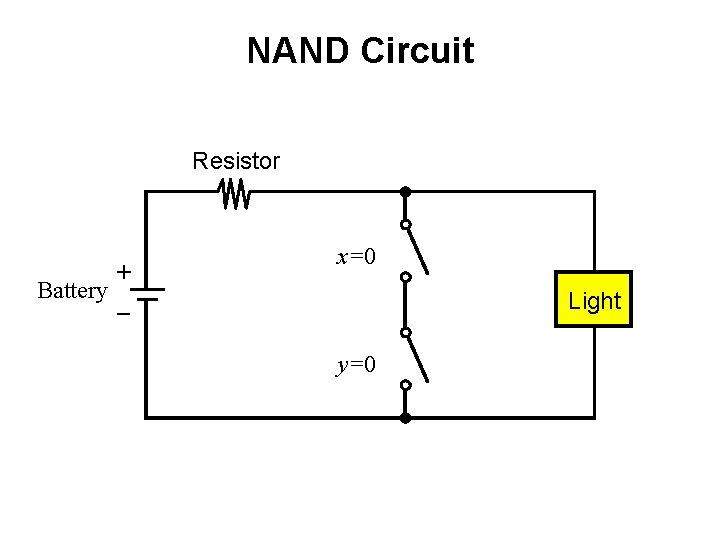
NAND Circuit Resistor + Battery _ x=0 Light y=0

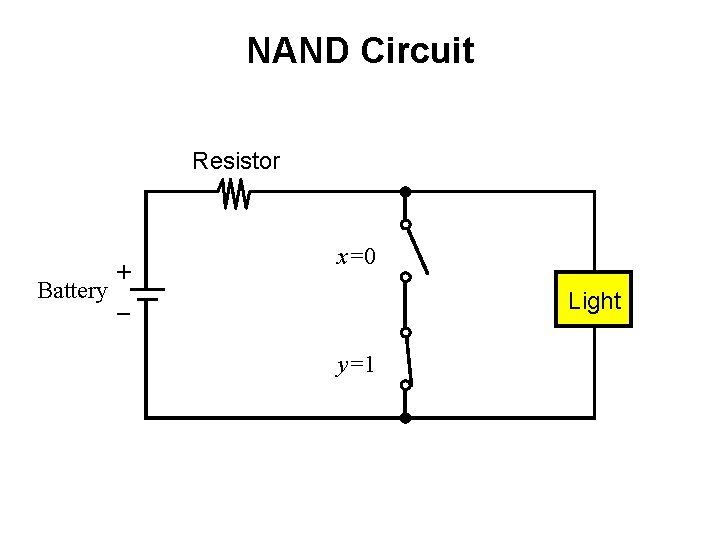
NAND Circuit Resistor + Battery _ x=0 Light y=1

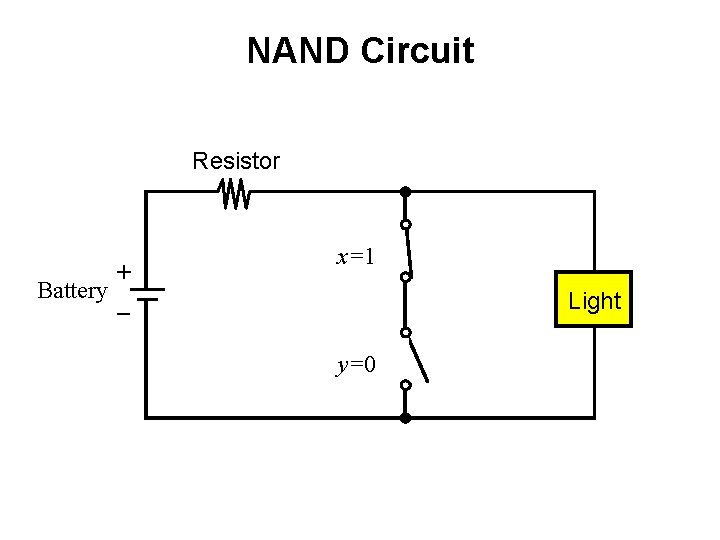
NAND Circuit Resistor + Battery _ x=1 Light y=0

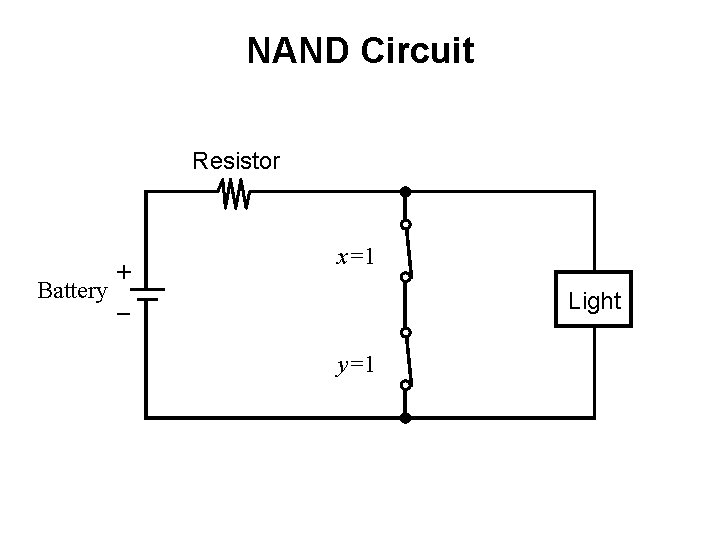
NAND Circuit Resistor + Battery _ x=1 Light y=1

NOR with Switches

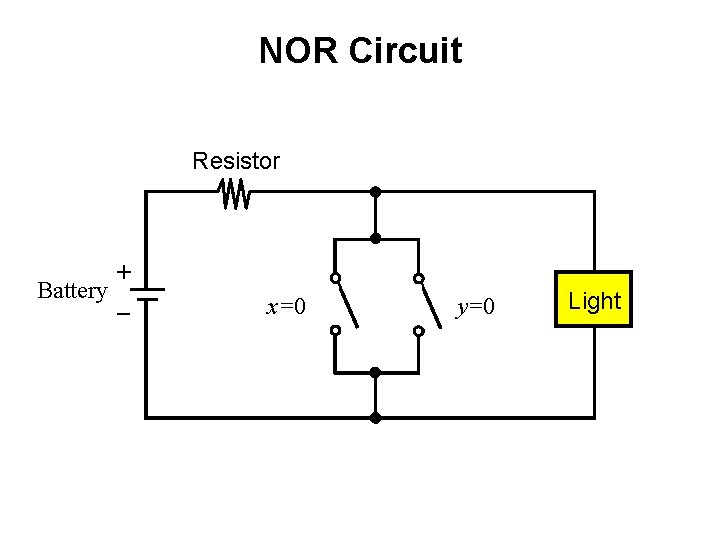
NOR Circuit Resistor + Battery _ x=0 y=0 Light

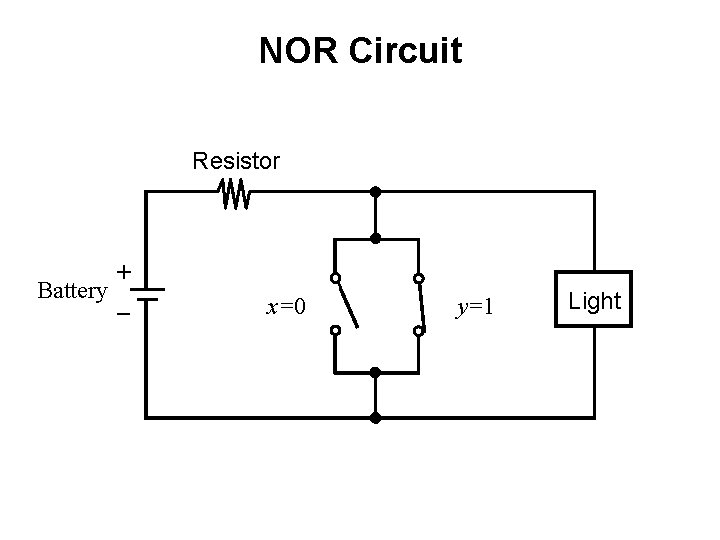
NOR Circuit Resistor + Battery _ x=0 y=1 Light

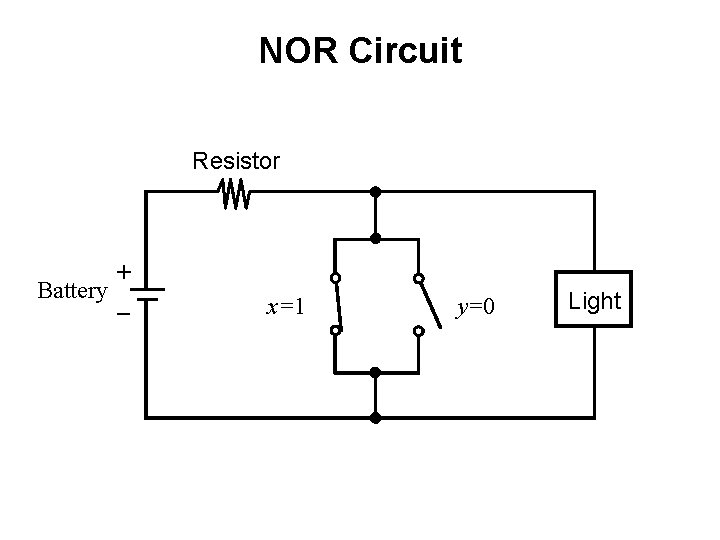
NOR Circuit Resistor + Battery _ x=1 y=0 Light

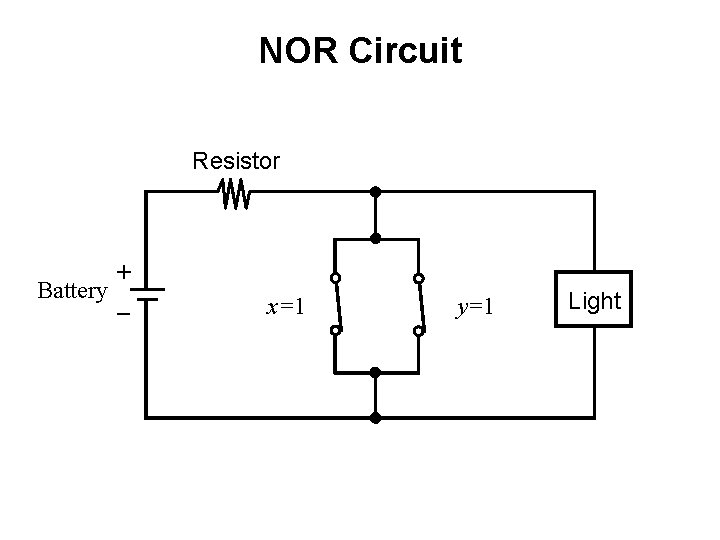
NOR Circuit Resistor + Battery _ x=1 y=1 Light

The Three Basic Logic Gates x x NOT x y AND x y OR 0 1 1 0 0 0 1 1 0 1 0 1 1 1 x x y x • y x +y

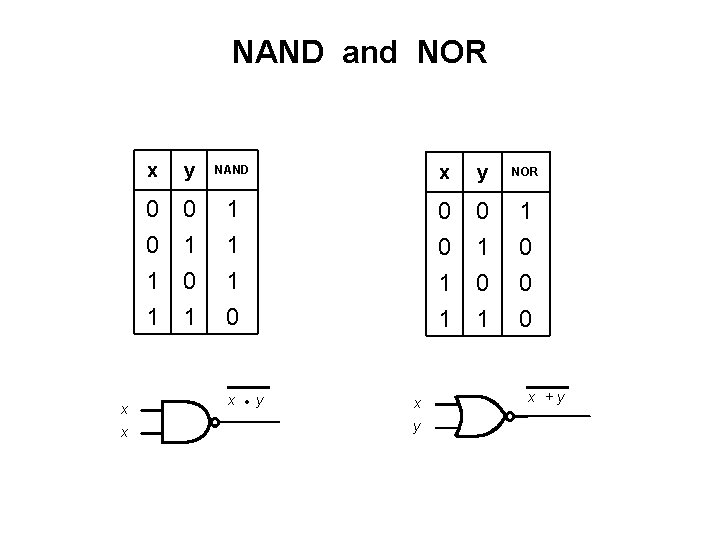
NAND and NOR x x x y NAND x y NOR 0 0 1 1 0 1 1 0 0 0 x • y x +y

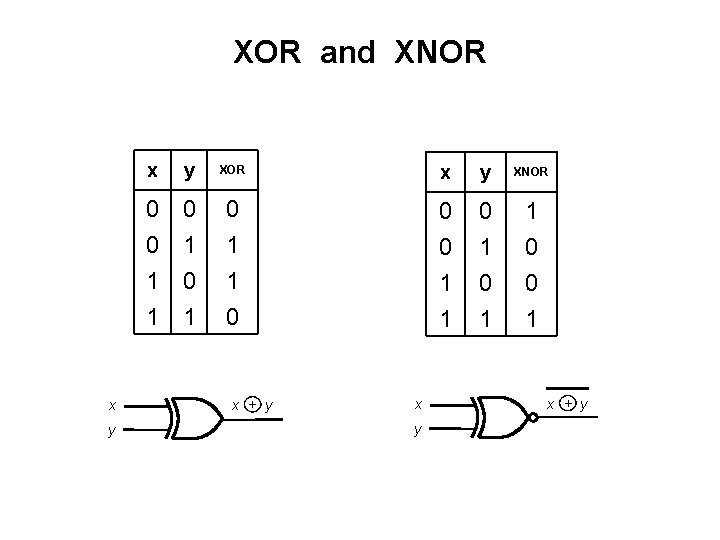
XOR and XNOR x y XOR x y XNOR 0 0 1 1 0 1 0 1 1 0 0 0 1 1 0 0 1 x + y

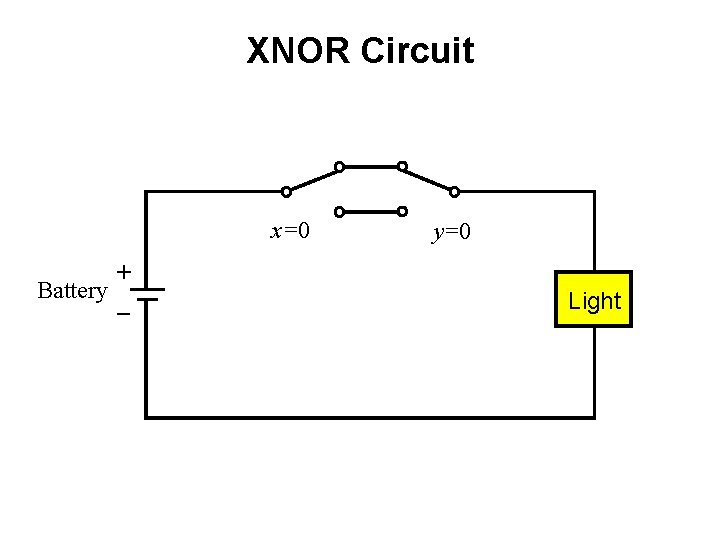
XNOR with Switches

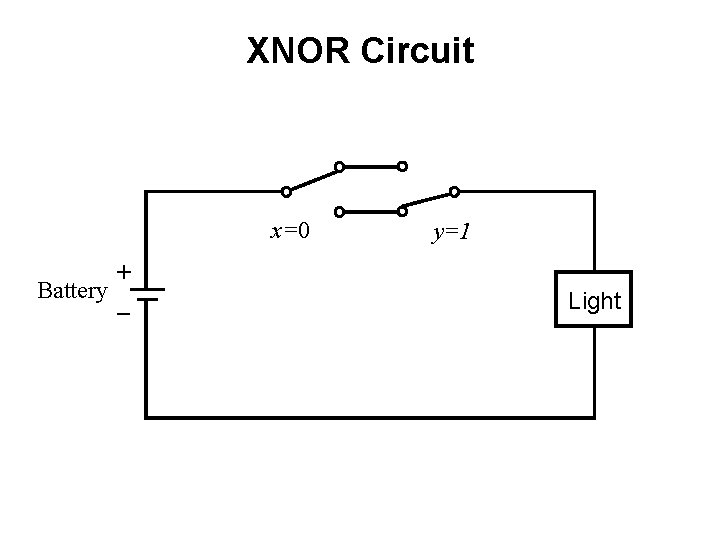
XNOR Circuit x=0 + Battery _ y=0 Light

XNOR Circuit x=0 + Battery _ y=1 Light

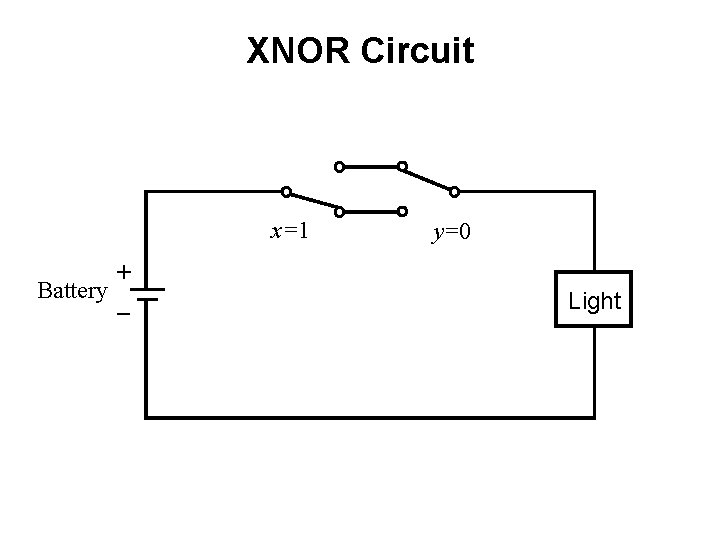
XNOR Circuit x=1 + Battery _ y=0 Light

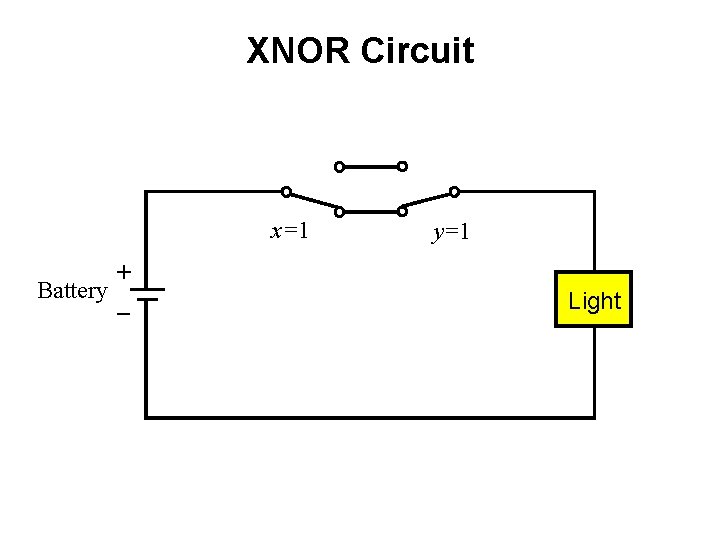
XNOR Circuit x=1 + Battery _ y=1 Light

XOR with Switches

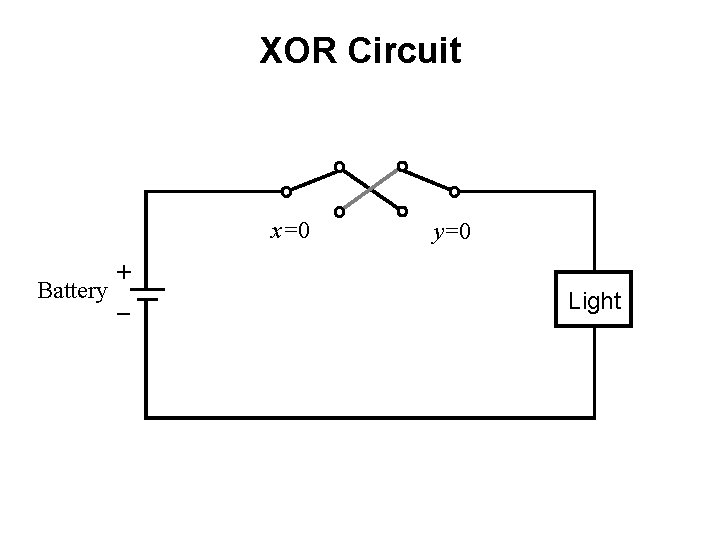
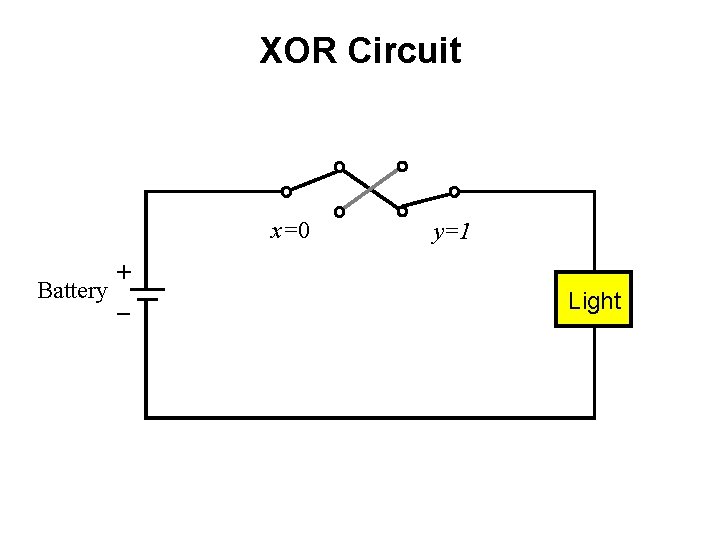
XOR Circuit x=0 + Battery _ y=0 Light

XOR Circuit x=0 + Battery _ y=1 Light

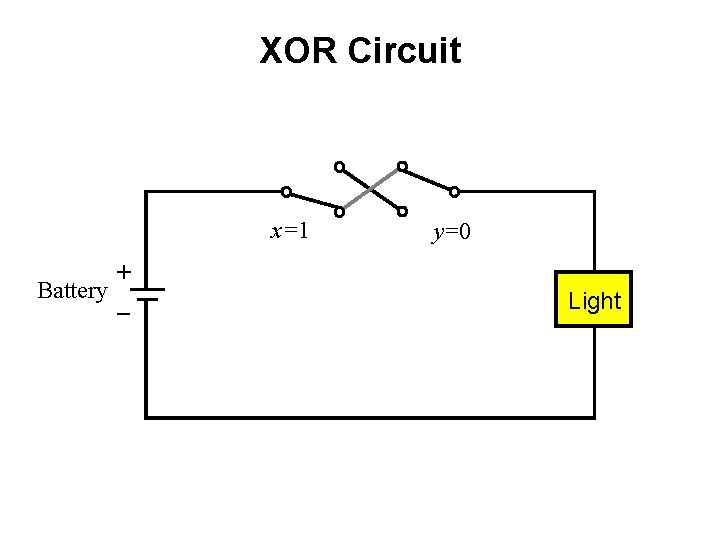
XOR Circuit x=1 + Battery _ y=0 Light

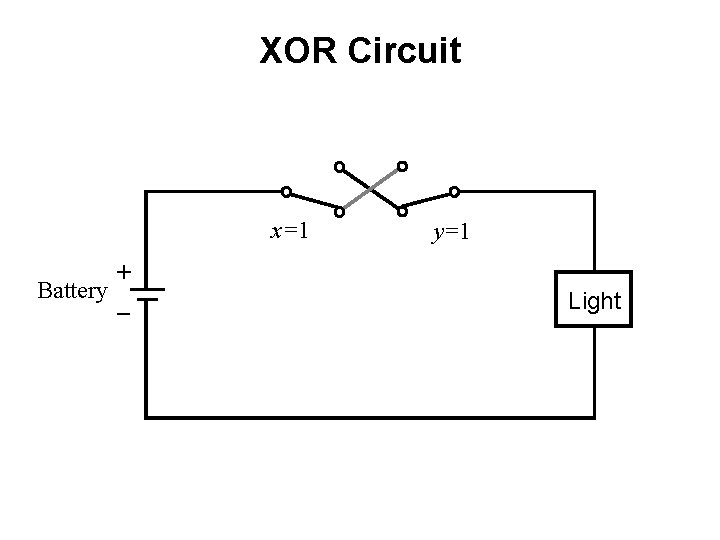
XOR Circuit x=1 + Battery _ y=1 Light

7 -Segment Display Example

7 -Segment Display a f g b c e d

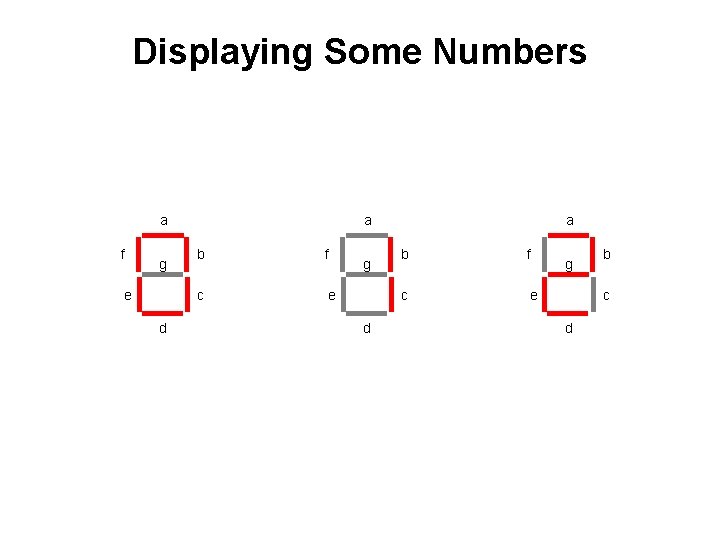
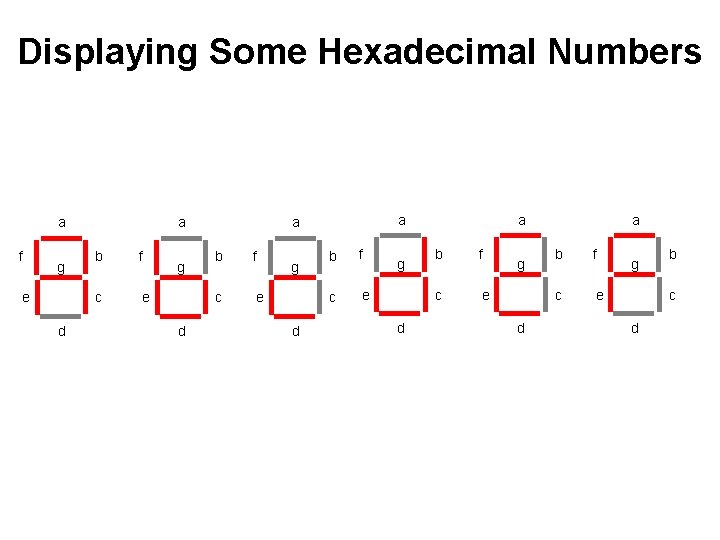
Displaying Some Numbers a f g e d a b f c e g b c d

Displaying Some Hexadecimal Numbers a f g e d a b f c e g d a b f c e g d a b f c e g b c d

Display of numbers [ Figure 2. 34 from the textbook ]

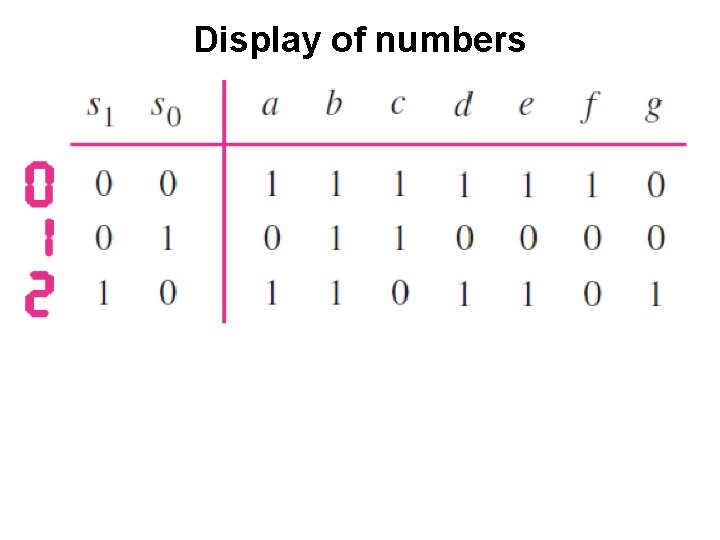
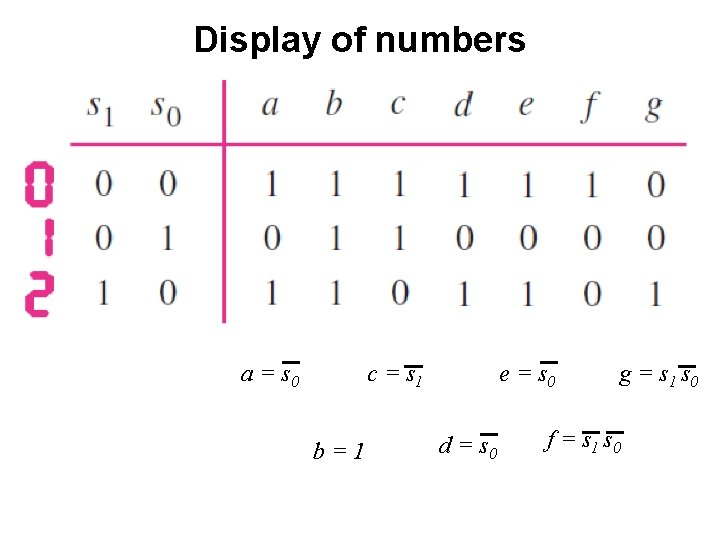
Display of numbers

Display of numbers a = s 0 c = s 1 b=1 e = s 0 d = s 0 g = s 1 s 0 f = s 1 s 0

Intro to Verilog

History • Created in 1983/1984 • Verilog-95 (IEEE standard 1364 -1995) • Verilog 2001 (IEEE Standard 1364 -2001) • Verilog 2005 (IEEE Standard 1364 -2005) • System. Verilog 2009 (IEEE Standard 1800 -2009).

HDL • Hardware Description Language • Verilog HDL • VHDL

Verilog HDL != VHDL • These are two different Languages! • Verilog is closer to C • VHDL is closer to Ada

[ Figure 2. 35 from the textbook ]

Sample Verilog Program

The Three Basic Logic Gates x x NOT gate x 1 x 2 x 1 • x 2 AND gate x 1 x 2 x 1 + x 2 OR gate You can build any circuit using only these three gates [ Figure 2. 8 from the textbook ]

How to specify a NOT gate in Verilog x x NOT gate

How to specify a NOT gate in Verilog we’ll use the letter y for the output x y NOT gate

How to specify a NOT gate in Verilog x y NOT gate not (y, x) Verilog code

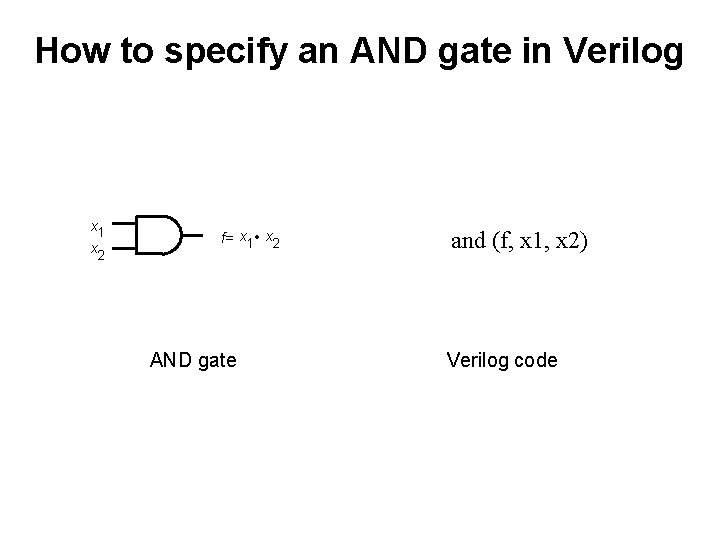
How to specify an AND gate in Verilog x 1 x 2 f= x 1 • x 2 AND gate and (f, x 1, x 2) Verilog code

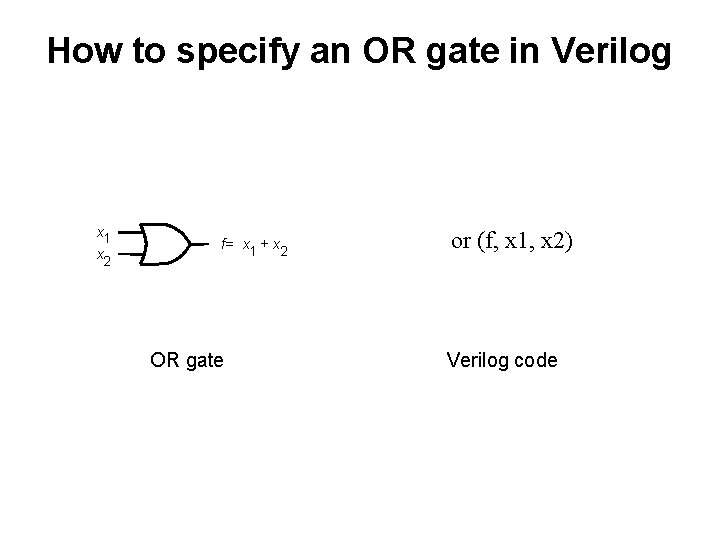
How to specify an OR gate in Verilog x 1 x 2 f= x 1 + x 2 OR gate or (f, x 1, x 2) Verilog code

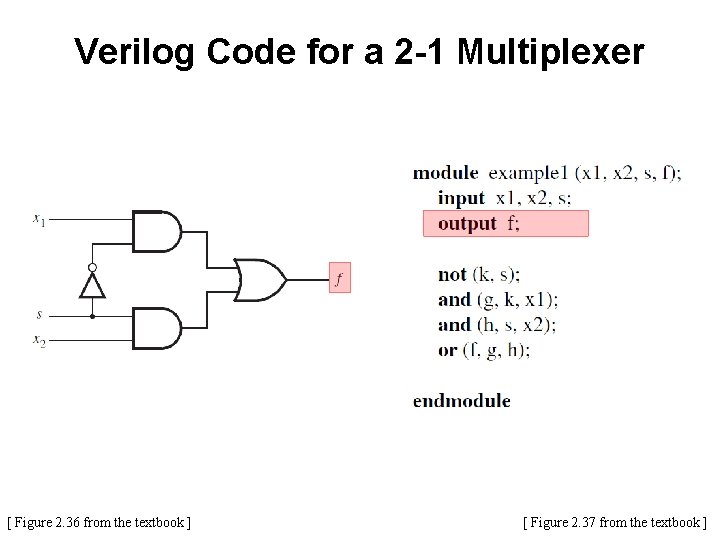
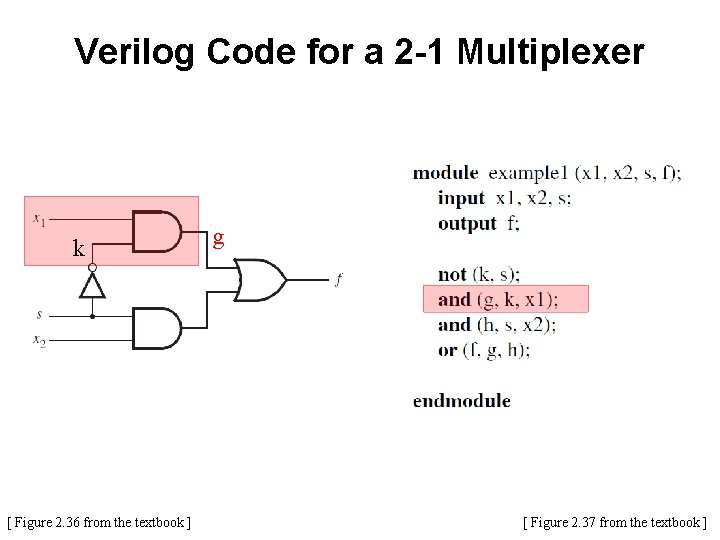
Specifying a 2 -to-1 Multiplexor in Verilog

2 -1 Multiplexer [ Figure 2. 36 from the textbook ]

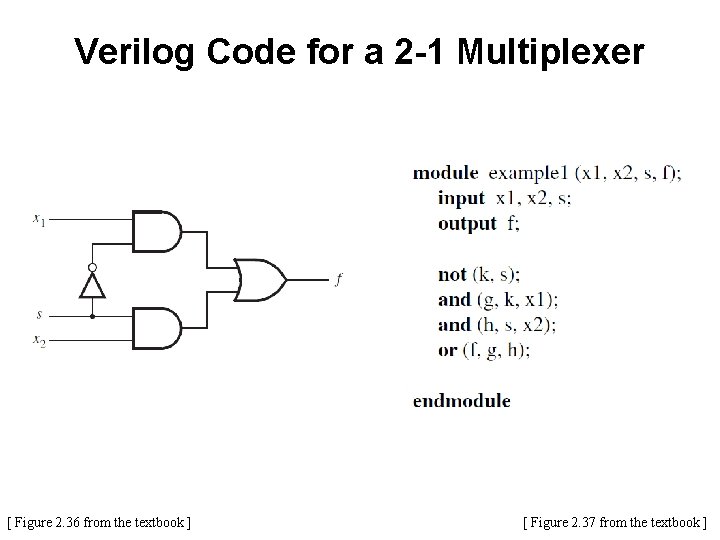
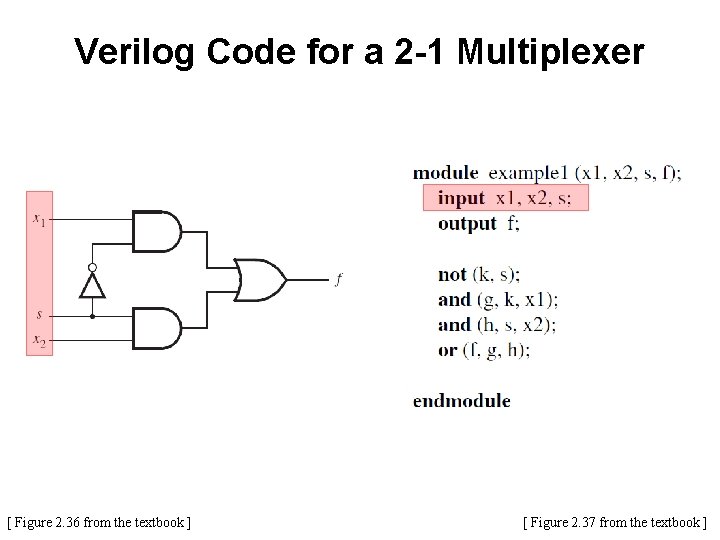
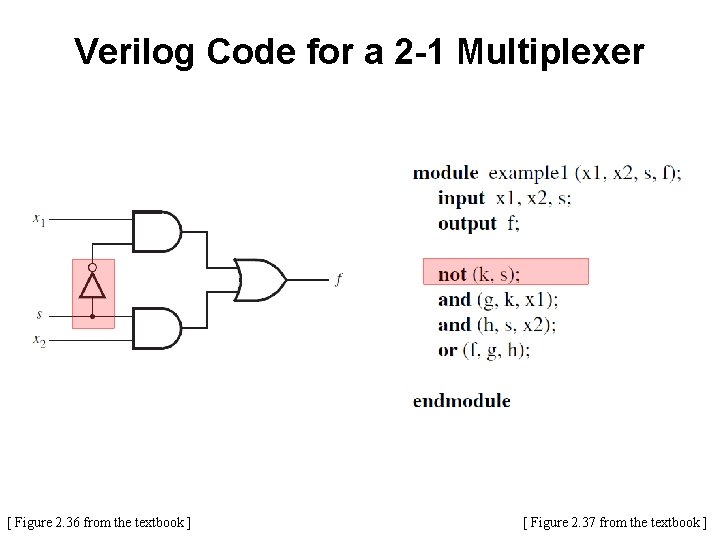
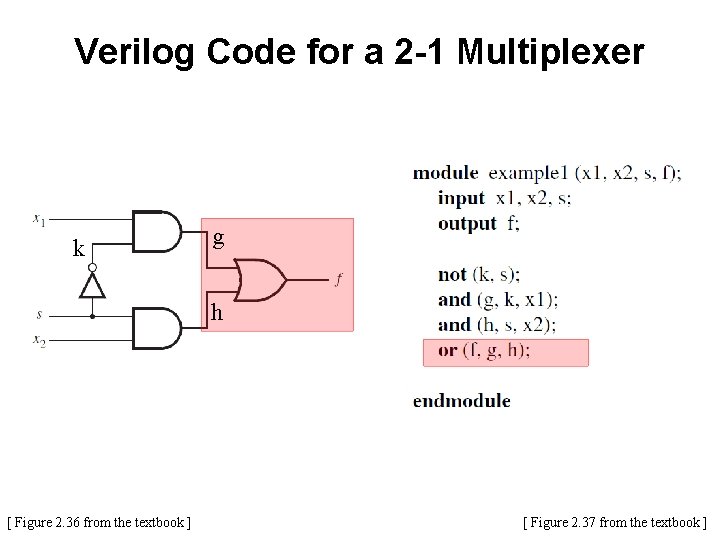
Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

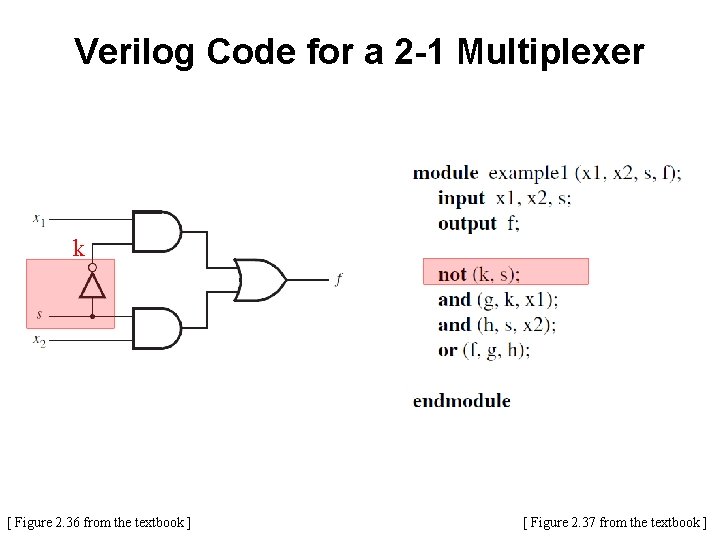
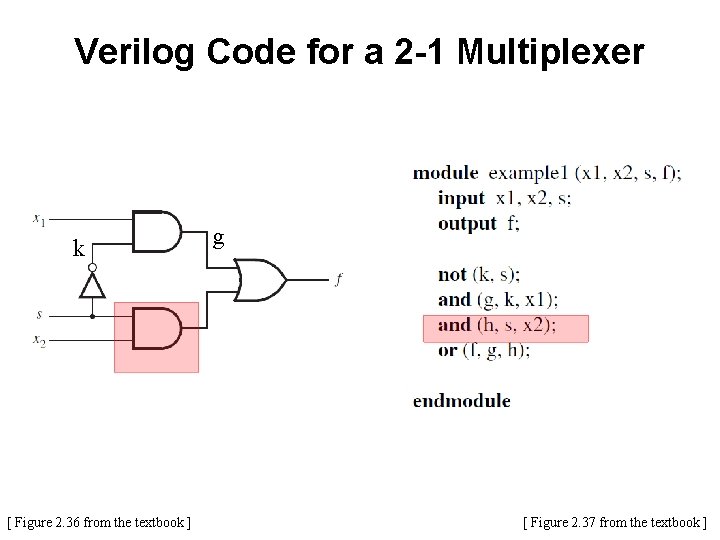
Verilog Code for a 2 -1 Multiplexer k [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer k [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

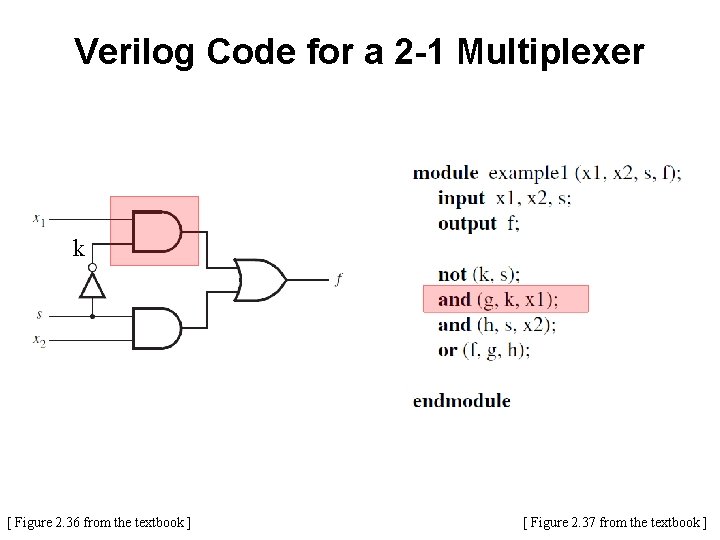
Verilog Code for a 2 -1 Multiplexer k [ Figure 2. 36 from the textbook ] g [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer k [ Figure 2. 36 from the textbook ] g [ Figure 2. 37 from the textbook ]

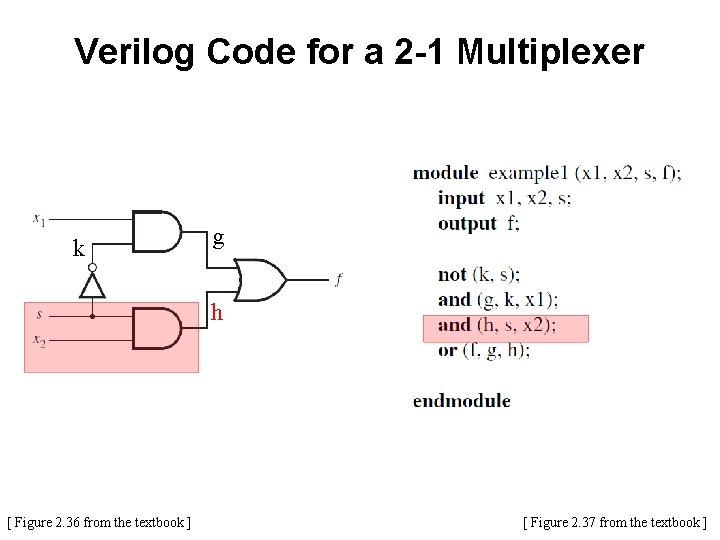
Verilog Code for a 2 -1 Multiplexer k g h [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer k g h [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

Verilog Code for a 2 -1 Multiplexer k g h [ Figure 2. 36 from the textbook ] [ Figure 2. 37 from the textbook ]

2 -to-1 Multiplexor in Verilog (with abbreviated syntax)

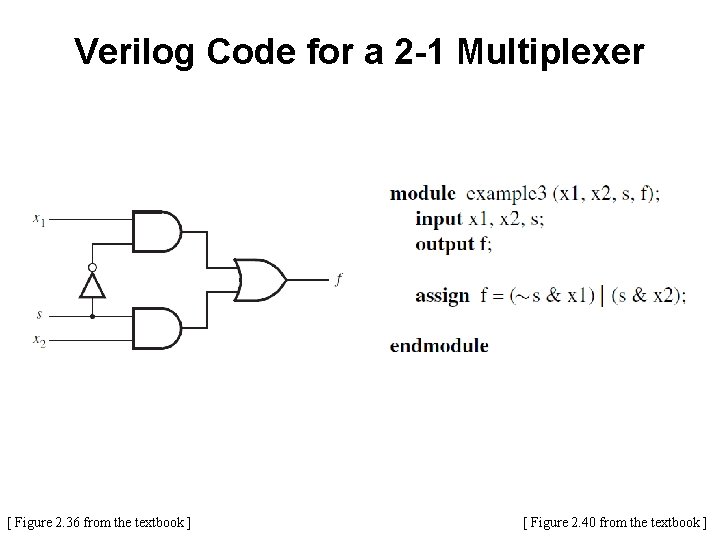
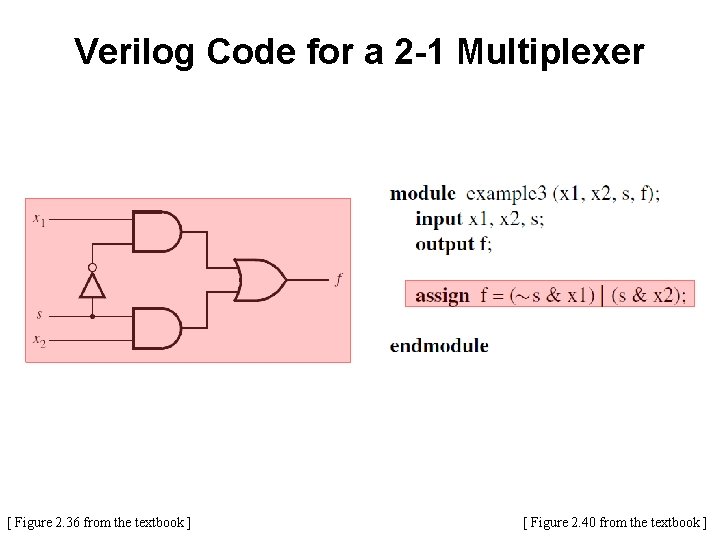
Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 40 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 40 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 40 from the textbook ]

Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 40 from the textbook ]

2 -to-1 Multiplexor in Verilog (with behavioral specification)

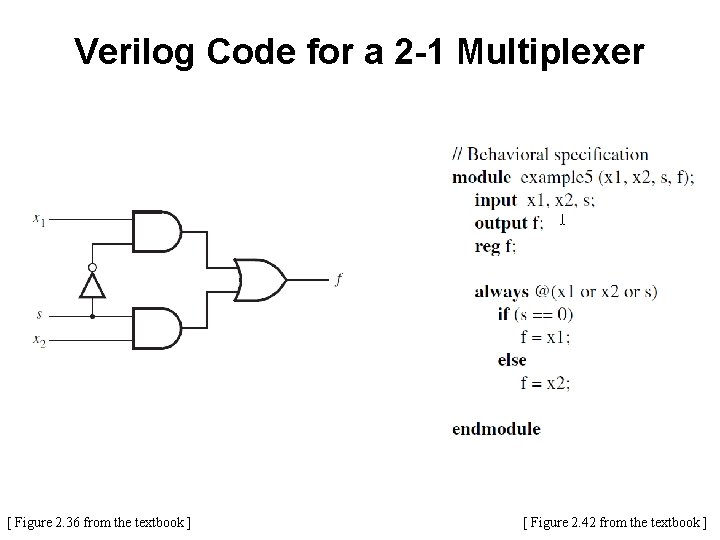
Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 42 from the textbook ]

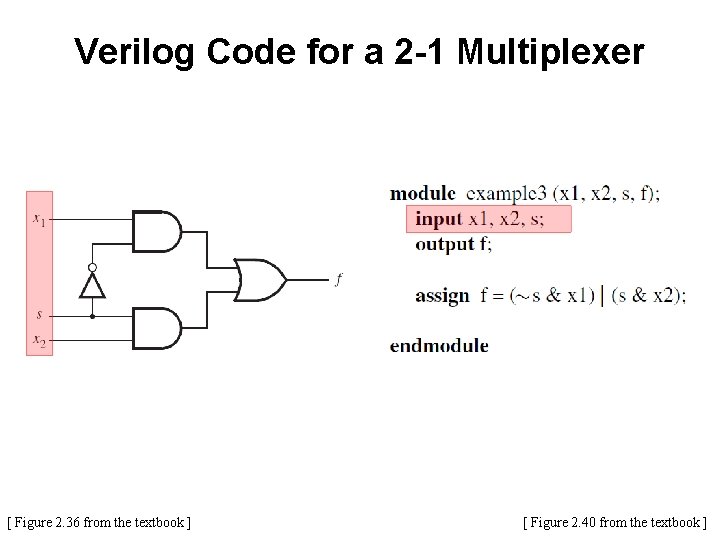
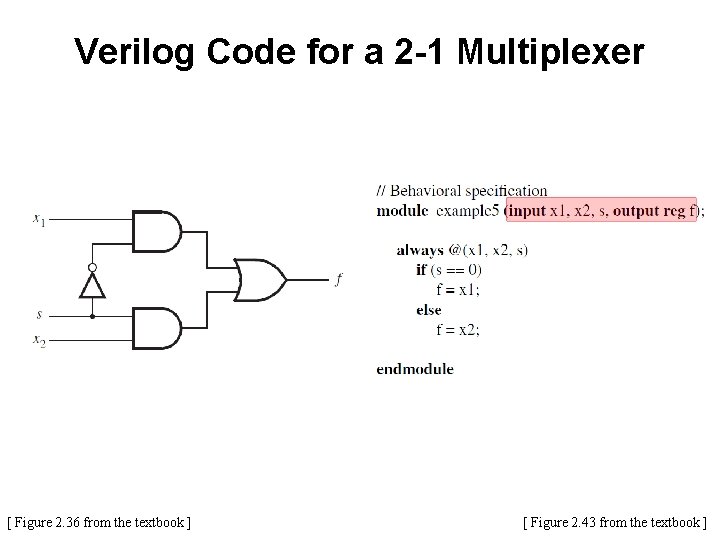
Verilog Code for a 2 -1 Multiplexer A 2 -to-1 Multiplexor has: • one output f • two inputs: x 1 and x 2 • It also has another input line s • If s=0, then the output is equal to x 1 • If s=1, then the output is equal to x 2 [ Figure 2. 36 from the textbook ] [ Figure 2. 42 from the textbook ]

Verilog Code for a 2 -1 Multiplexer A 2 -to-1 Multiplexor has: • one output f • two inputs: x 1 and x 2 • It also has another input line s • If s=0, then the output is equal to x 1 • If s=1, then the output is equal to x 2 [ Figure 2. 36 from the textbook ] [ Figure 2. 42 from the textbook ]

always@ syntax always @(x, y) always @(x or y) always @(*) always @*

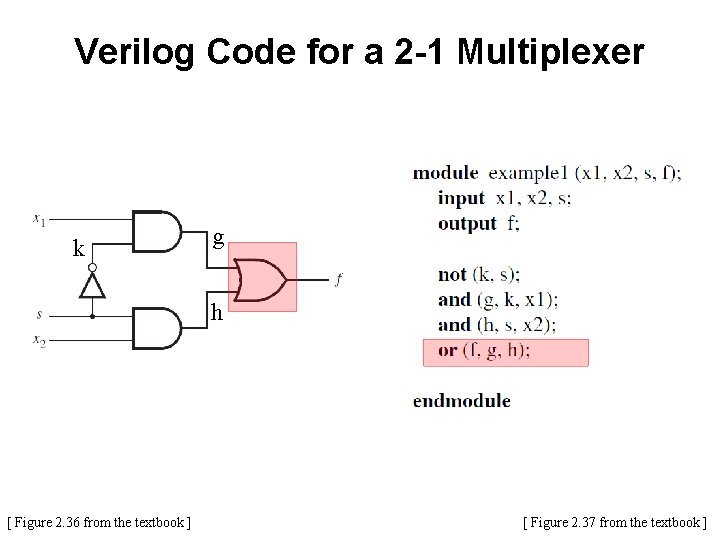
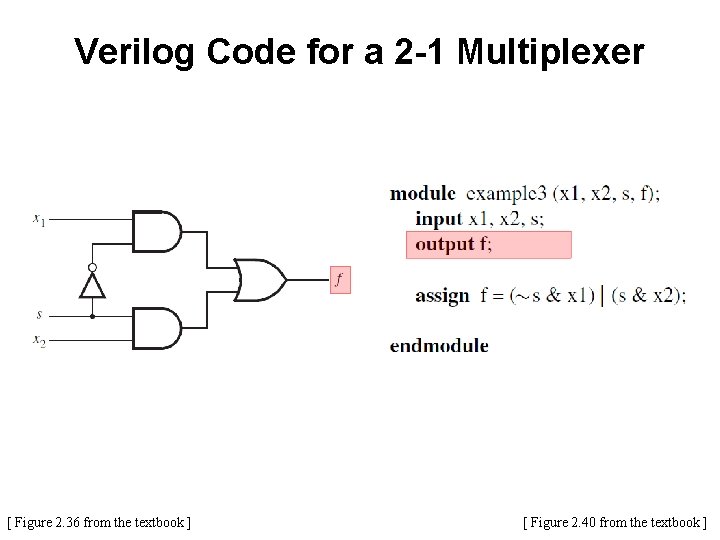
Verilog Code for a 2 -1 Multiplexer [ Figure 2. 36 from the textbook ] [ Figure 2. 43 from the textbook ]

Another Example

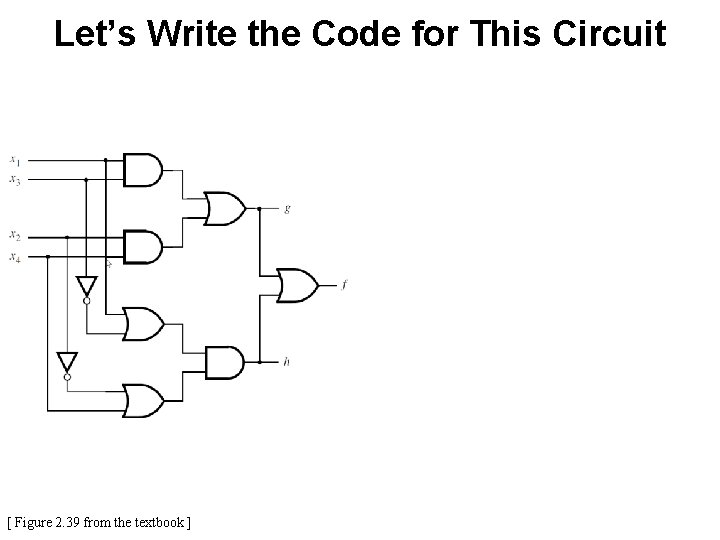
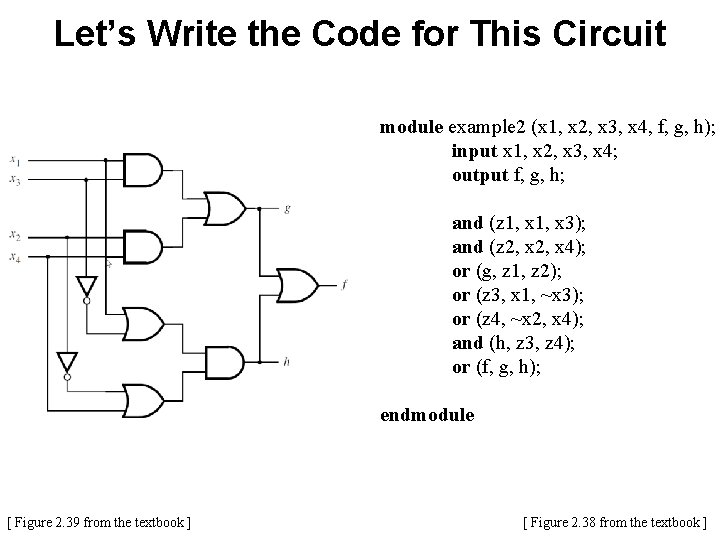
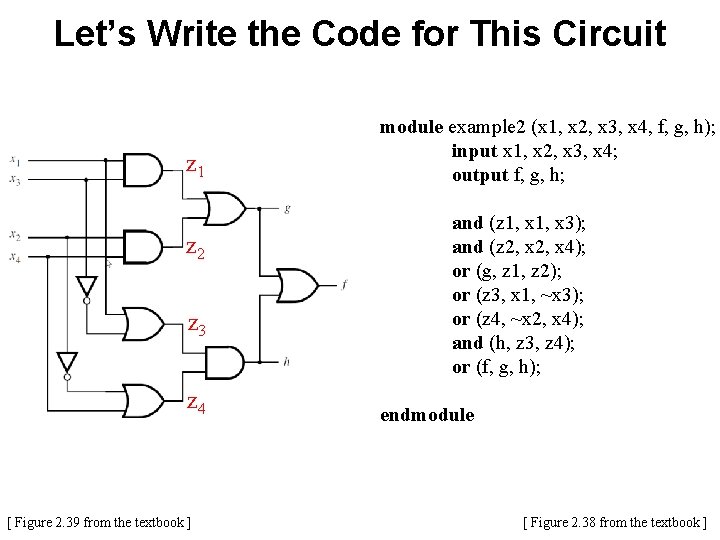
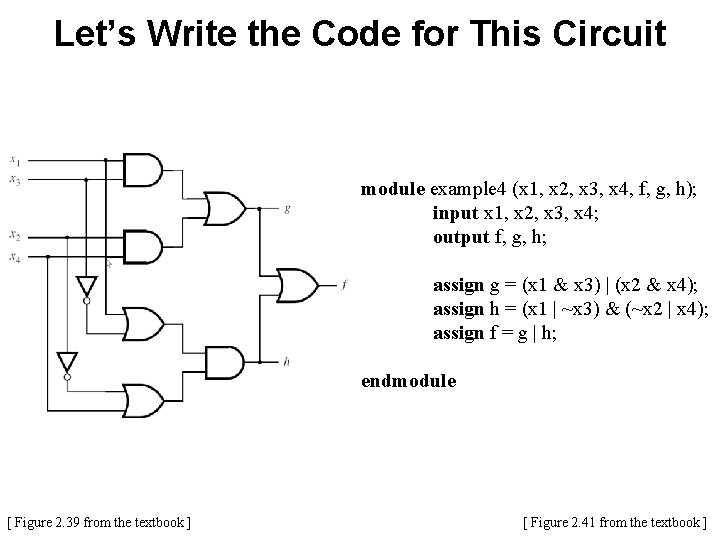
Let’s Write the Code for This Circuit [ Figure 2. 39 from the textbook ]

Let’s Write the Code for This Circuit module example 2 (x 1, x 2, x 3, x 4, f, g, h); input x 1, x 2, x 3, x 4; output f, g, h; and (z 1, x 3); and (z 2, x 4); or (g, z 1, z 2); or (z 3, x 1, ~x 3); or (z 4, ~x 2, x 4); and (h, z 3, z 4); or (f, g, h); endmodule [ Figure 2. 39 from the textbook ] [ Figure 2. 38 from the textbook ]

Let’s Write the Code for This Circuit z 1 z 2 z 3 z 4 [ Figure 2. 39 from the textbook ] module example 2 (x 1, x 2, x 3, x 4, f, g, h); input x 1, x 2, x 3, x 4; output f, g, h; and (z 1, x 3); and (z 2, x 4); or (g, z 1, z 2); or (z 3, x 1, ~x 3); or (z 4, ~x 2, x 4); and (h, z 3, z 4); or (f, g, h); endmodule [ Figure 2. 38 from the textbook ]

Let’s Write the Code for This Circuit module example 4 (x 1, x 2, x 3, x 4, f, g, h); input x 1, x 2, x 3, x 4; output f, g, h; assign g = (x 1 & x 3) | (x 2 & x 4); assign h = (x 1 | ~x 3) & (~x 2 | x 4); assign f = g | h; endmodule [ Figure 2. 39 from the textbook ] [ Figure 2. 41 from the textbook ]

Yet Another Example

A logic circuit with two modules [ Figure 2. 44 from the textbook ]

The adder module [ Figure 2. 12 from the textbook ]

The adder module [ Figure 2. 45 from the textbook ]

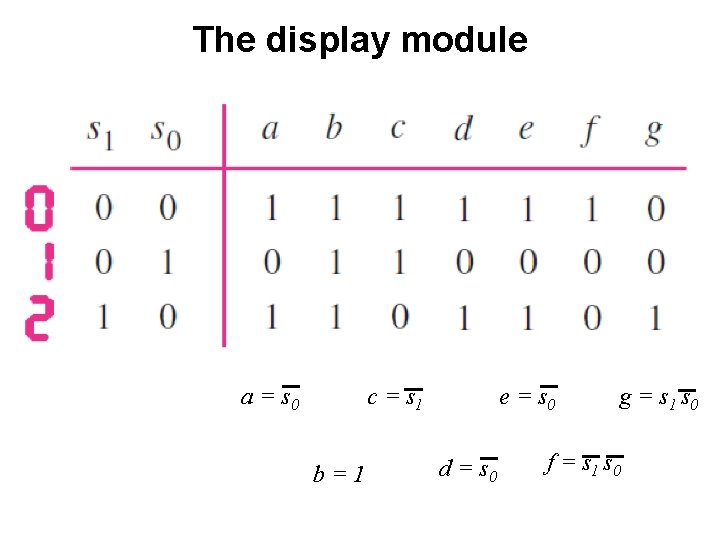
The display module a = s 0 c = s 1 b=1 e = s 0 d = s 0 g = s 1 s 0 f = s 1 s 0

The display module a = s 0 b=1 c = s 1 d = s 0 e = s 0 f = s 1 s 0 g = s 1 s 0 [ Figure 2. 46 from the textbook ]

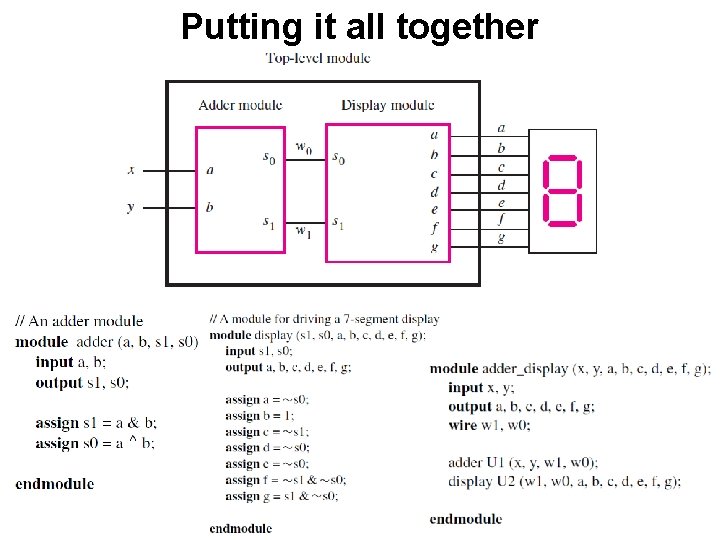
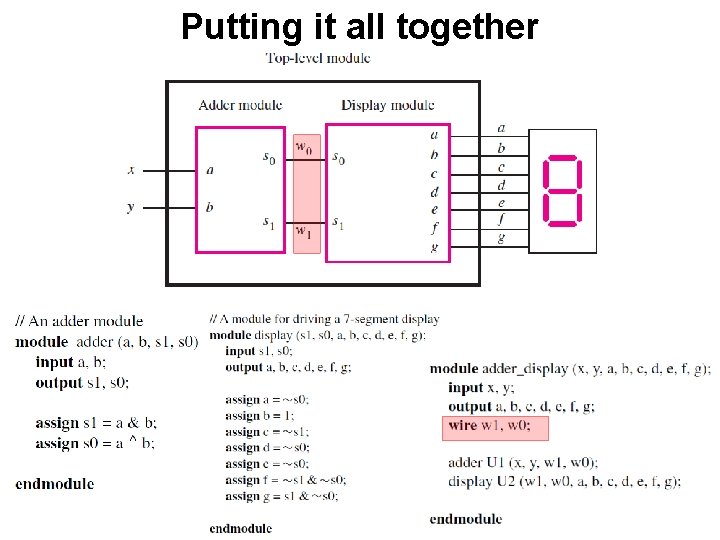
Putting it all together

Putting it all together

Questions?

THE END