Cpr E 185 Intro to Problem Solving using

Cpr. E 185: Intro to Problem Solving (using C) Instructor: Alexander Stoytchev http: //www. cs. iastate. edu/~alex/classes/2008_Fall_185/

Administrative Stuff • Midterm 2 is next week!!! • Same format as before: § Lab exam during your regular lab time (Oct 28 or Oct 29) § Lecture exam on Oct 29 (10 -11 am) § Note: There will be NO night exam. • The exam will be cumulative with emphasis on conditional statements (if, if-else, switch), loops (do, while, for), arrays (to be covered), and searching and sorting algorithms (to be covered).

Administrative Stuff • HW 7 is out today. It’s due next Monday @ 8 pm. • HW 6 is due this Friday (Oct 24) @ 8 pm.

Other Stuff in Chapter 8

Two-Dimensional Arrays • int Matrix[2][3]; • Defines the following elements: § Row 1: Matrix[0][0], Matrix[0][1], Matrix[0][2] § Row 2: Matrix[1][0], Matrix[1][1], Matrix[1][2]

Two-Dimensional Arrays int Matrix[2][3]; • Initialization: Matrix[0][0]=3; Matrix[0][1]=4; Matrix[0][2]=5; Matrix[1][0]=1; Matrix[1][1]= -20; Matrix[1][2]=7;

Two-Dimensional Arrays • Initialization when defined: int Matrix[2][3] = { {3, 4, 5}, {1, -20, 7};

Two-Dimensional Arrays • 2 D arrays and nested for loop int Matrix[2][3] = { {3, 4, 5}, {1, -20, 7}}; int i, j; for(i=0; i< 2; i++) { for(j=0; j<3; j++) printf(“%3 d ”, Matrix[i][j]); printf(“n”); }

Sorting Algorithms Cpr. E 185: Intro to Problem Solving Iowa State University, Ames, IA

Quick Review of the Last Lecture

Problem: Find the minimum number in an array of unsorted integers find_minimum. c

Search [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 011. htm]

Linear Search • The most basic • Very easy to implement • The array DOESN’T have to be sorted • All array elements must be visited if the search fails • Could be very slow

Example: Successful Linear Search [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 011. htm]

Example: Failed Linear Search [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 011. htm]

Problem: Find the index of a number in an unsorted array of integers linear_search. c

Problem: Find the all occurrences of a number in an array and replace it with a new value. search_and_replace. c

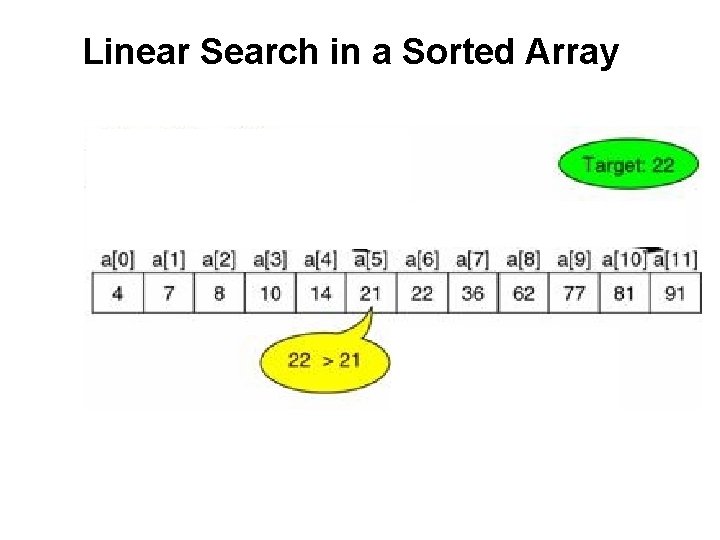
Linear Search in a Sorted Array

Problem: Find the index of a number in a sorted array of integers Linear. Search_In. Sorted. Array. c

Analysis • If the list is unsorted we have to search all numbers before we declare that the target is not present in the array. • Because the list is sorted we can stop as soon as we reach a number that is greater than our target • Can we do even better?

Binary Search • At each step it splits the remaining array elements into two groups • Therefore, it is faster than the linear search • Works only on an already SORTED array • Thus, there is a performance penalty for sorting the array [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 011. htm]

Example: Successful Binary Search [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 011. htm]

Example: Binary. Search. c

Analysis of Searching Methods • For an array of size n • Sequential Search (Average-Case) • Sequential Search (Worst-Case) n/2 n • Binary Search (Average-Case) • Binary Search (Worst-Case) log(n)/2 log(n)

Chapter 8 (Sorting)

Insertion Sort 0 [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Analogy: Sorting Cards

Example: Insertion Sort [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Animations for Insertion Sort [http: //maven. smith. edu/~thiebaut/java/sort/demo. html]

Animations of Sorting Algoritms • http: //maven. smith. edu/~thiebaut/java/sort/demo. html • http: //www. cs. ubc. ca/spider/harrison/Java/sorting-demo. html

Swapping Array Elements [http: //www. scs. ryerson. ca/jpanar/w 2006/cps 125/example. gifs/ch 7/Arr. Swap. gif]

C code // Swap a[i] with the smallest element int temp = a[i]; a[i] = a[min. Index]; a[min. Index] = temp;

Example: Insertion. Sort. c

Selection Sort [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Example: Selection Sort [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Example: Selection. Sort. c

Bubble Sort 0 [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Example: Bubble Sort [http: //web. ics. purdue. edu/~cs 154/lectures/lecture 010. htm]

Example: Bubble. Sort. c

Analysis: all three run in O(n 2) time [http: //linux. wku. edu/~lamonml/algor/sort. html]

Analysis • There are faster sorting algorithms § Heap sort § Quick sort § Merge Sort • We will not cover those but feel free to study them on your own. • They run in O(n log n) time.

O(n log n) sorting algorithms [http: //linux. wku. edu/~lamonml/algor/sort. html]

Questions?

THE END