CPCTC Be able to use CPCTC to find

CPCTC Be able to use CPCTC to find unknowns in congruent triangles! Quick Review Are these triangles congruent? By which postulate/theorem? L J N K _____ M Oh, and what is the Reflexive Property again? It says something is equal to itself. EX: A A or AB AB.

CPCTC Once you have shown triangles are congruent, then you can make some CONCLUSIONS about all of the corresponding parts (_______ of sides and _____) angles those triangles! Corresponding Parts of Congruent Triangles are CONGRUENT!! C. P. C . T. C.

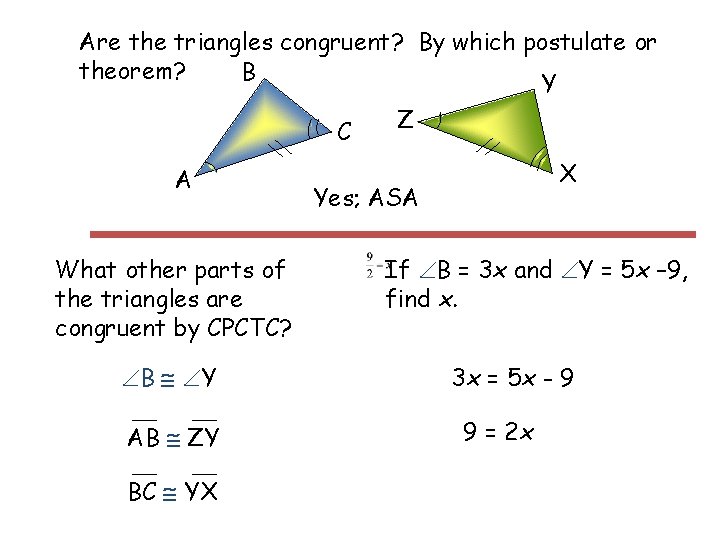
Are the triangles congruent? By which postulate or theorem? B Y Z C A What other parts of the triangles are congruent by CPCTC? B Y AB ZY BC YX X Yes; ASA If B = 3 x and Y = 5 x – 9, find x. 3 x = 5 x - 9 9 = 2 x

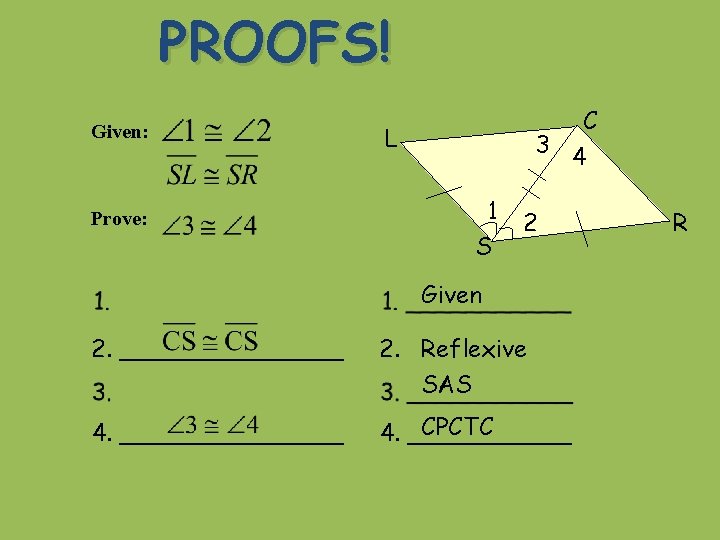
PROOFS! Given: Prove: C L 3 4 1 S 2 Given 2. ________ 2. Reflexive SAS 4. ________ CPCTC 4. ______ R

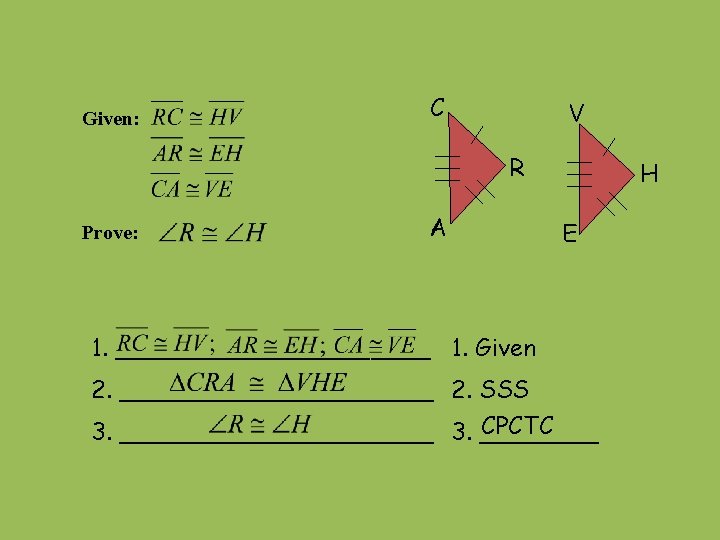
Given: C V R Prove: A H E 1. ___________ 1. Given 2. ___________ 2. SSS CPCTC 3. ___________ 3. ____

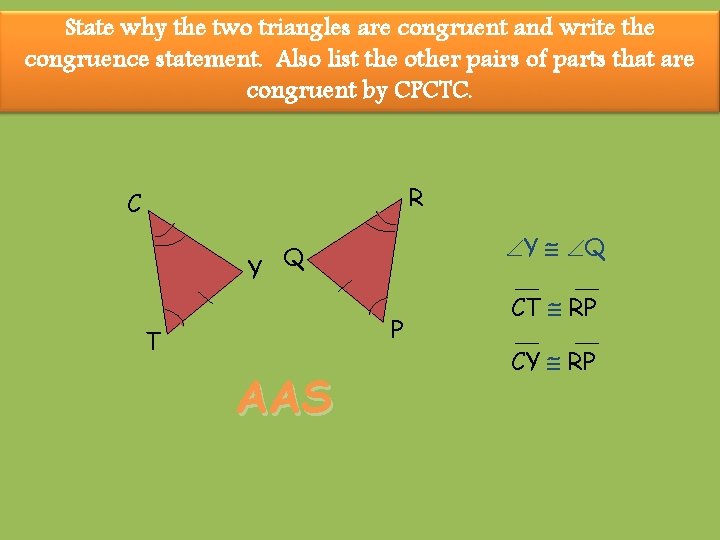
State why the two triangles are congruent and write the congruence statement. Also list the other pairs of parts that are congruent by CPCTC. R C Y Q Y Q P T AAS CT RP CY RP

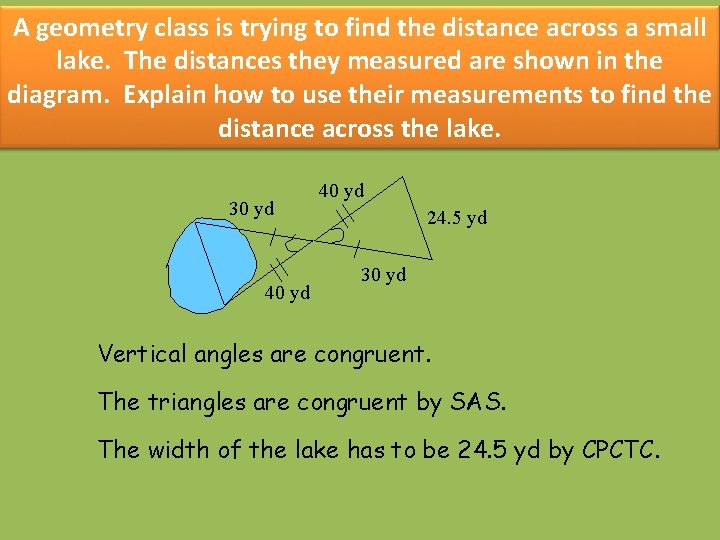
A geometry class is trying to find the distance across a small lake. The distances they measured are shown in the diagram. Explain how to use their measurements to find the distance across the lake. 30 yd 40 yd 24. 5 yd 30 yd Vertical angles are congruent. The triangles are congruent by SAS. The width of the lake has to be 24. 5 yd by CPCTC.

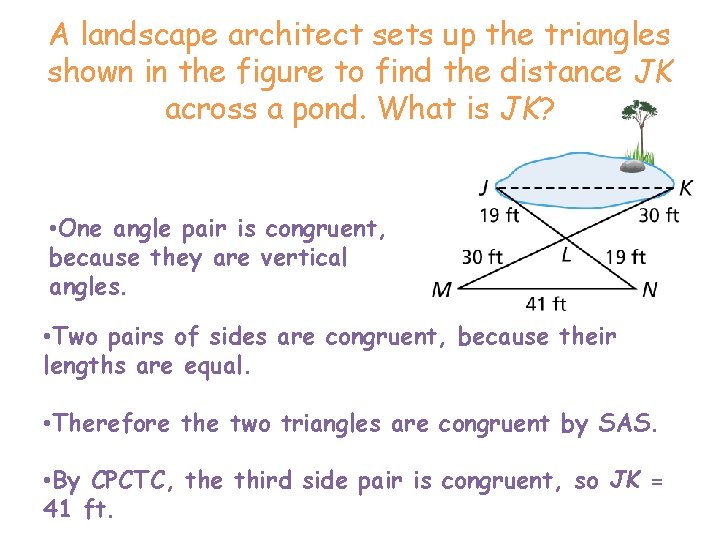
A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? • One angle pair is congruent, because they are vertical angles. • Two pairs of sides are congruent, because their lengths are equal. • Therefore the two triangles are congruent by SAS. • By CPCTC, the third side pair is congruent, so JK = 41 ft.

Given: NO || MP, N P Prove: MN || OP Statements Reasons 1. N P; NO || MP 1. Given 2. NOM PMO 2. Alt. Int. s Thm. 3. MO 3. Reflex. Prop. of 4. ∆MNO ∆OPM 4. AAS 5. NMO POM 5. CPCTC 6. MN || OP 6. Conv. Of Alt. Int. s Thm.

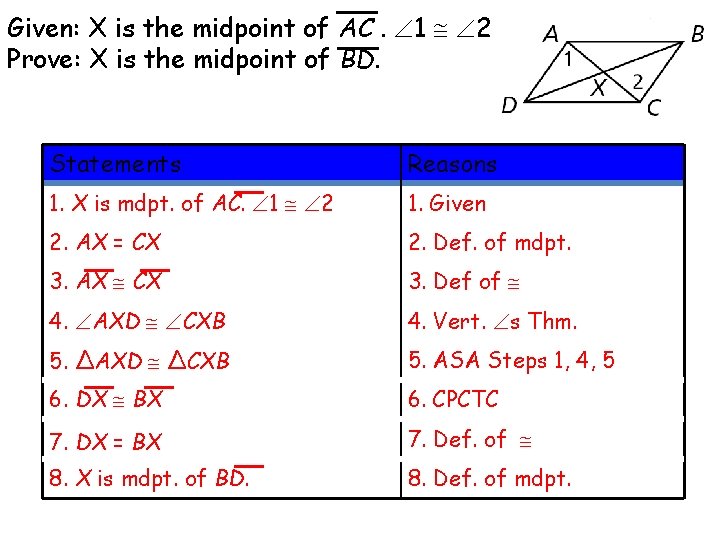
Given: X is the midpoint of AC. 1 2 Prove: X is the midpoint of BD. Statements Reasons 1. X is mdpt. of AC. 1 2 1. Given 2. AX = CX 2. Def. of mdpt. 3. AX CX 3. Def of 4. AXD CXB 4. Vert. s Thm. 5. ∆AXD ∆CXB 5. ASA Steps 1, 4, 5 6. DX BX 6. CPCTC 7. DX = BX 7. Def. of 8. X is mdpt. of BD. 8. Def. of mdpt.