CP EJE RADICAL CP5 Prof Jos Juan Aliaga

CP: EJE RADICAL CP_5 Prof. José Juan Aliaga Maraver

Lugar Geométrico de la Suma/Diferencia de cuadrados de distancias a dos puntos fijos A b 2 = h 2 + ( a/2 – MH )2 c c 2 = h 2 + ( a/2 + MH )2 m 2 = h 2 + MH 2 m h M H B a/2 a b 2 + c 2 = 2 h 2 + a 2/2 + 2 MH 2 = a 2/2 +2 m 2 b 2 - c 2 = - 2 a. MH b C

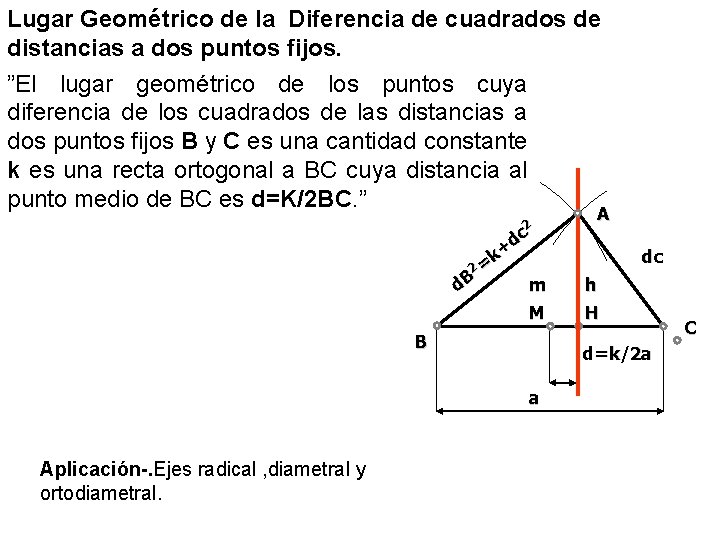
Lugar Geométrico de la Diferencia de cuadrados de distancias a dos puntos fijos. ”El lugar geométrico de los puntos cuya diferencia de los cuadrados de las distancias a dos puntos fijos B y C es una cantidad constante k es una recta ortogonal a BC cuya distancia al punto medio de BC es d=K/2 BC. ” 2 dc k+ 2= B m d h M H B dc d=k/2 a a Aplicación-. Ejes radical , diametral y ortodiametral. A C

Lugar Geométrico de la Diferencia de cuadrados de distancias a dos puntos fijos. b 2 - c 2 = - 2 a. MH = cte • Al ser fija la distancia entre los puntos, “a” es constante A • Para que la igualdad sea constante la distancia “MH” tiene que serlo también c • “MH” es la proyección de la mediana sobre “BC” b m h M H B a/2 a • para que la proyección de la mediana sobre “BC” permanezca constante, el punto “A” tiene que moverse sobre la recta “h” C

Eje radical • El eje radical de dos circunferencias es el lugar geométrico de los puntos del plano – que son centros de circunferencias ortogonales a dichas circunferencias – que tienen igual potencia respecto a dichas circunferencias – desde los cuales se pueden trazar segmentos tangentes de igual longitud a las circunferencias

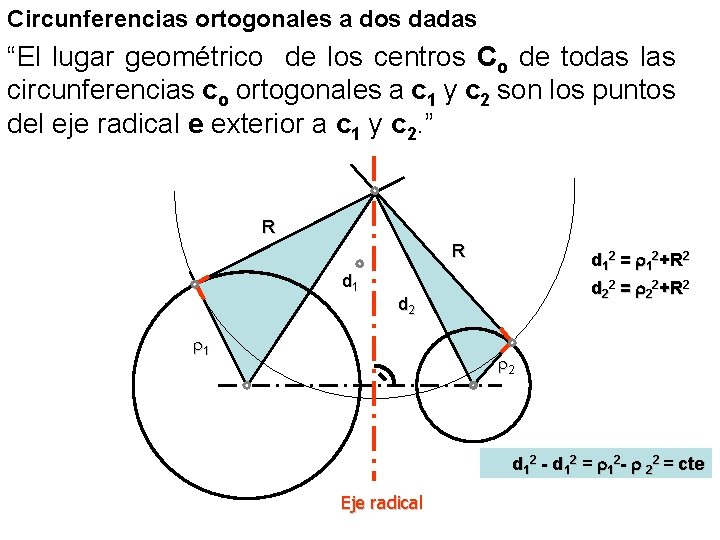
Circunferencias ortogonales a dos dadas “El lugar geométrico de los centros Co de todas las circunferencias co ortogonales a c 1 y c 2 son los puntos del eje radical e exterior a c 1 y c 2. ” R R d 1 2 = 1 2 + R 2 d 2 2 = 2 2 + R 2 d 2 1 2 d 12 - d 12 = 12 - 22 = cte Eje radical

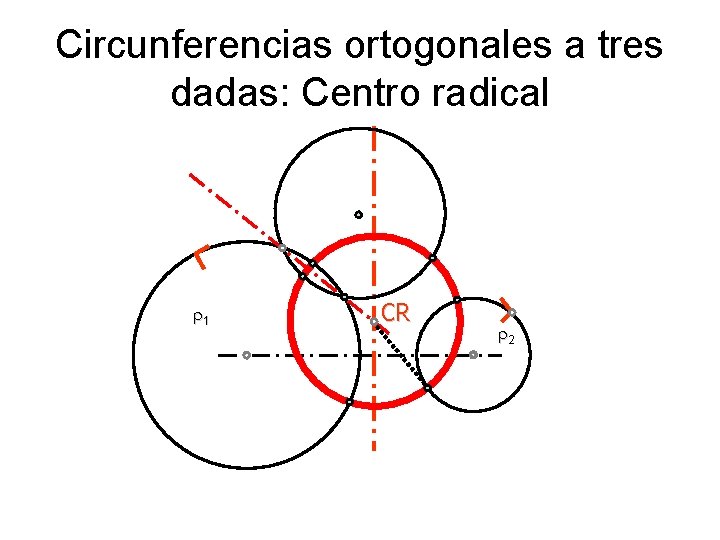
Centro radical de tres circunferencias • El Centro radical CR de tres circunferencias coplanarias es un punto de su plano: – es intersección de los tres ejes radicales de las circunferencias – tiene igual potencia respecto a dichas circunferencias – es centro de la circunferencia ortogonal a dichas circunferencias – desde el cual se pueden trazar segmentos tangentes de igual longitud a las tres circunferencias

Determinación del eje radical • Dirección perpendicular a la recta base de los centros Potencia nula

Determinación del eje radical • Dirección perpendicular a la recta base de los centros CR Circunferencia auxiliar

Circunferencias ortogonales a tres dadas: Centro radical 1 CR 2

Casos singulares • • • Eje radical de dos puntos Eje radical de punto y circunferencia Eje radical de punto y recta ? Eje radical de circunferencia y recta ? Eje radical de dos rectas ?

CP_5 P_01 Potencia de un punto respecto de una circunferencia Trazar la circunferencia ortogonal a c 1, c 2 y c 3. Analizar diferentes modelos de solución y de datos

CP_5 P_02 Potencia de un punto respecto de una circunferencia Trazar las circunferencias de centros A, B y C y la condición de que sean tangentes dos a dos exteriormente. A B C

CP_5 P_03 Potencia de un punto respecto de una circunferencia Dados los puntos A, B y C, trazar tres circunferencia tangentes dos a dos con puntos de tangencia en dichos puntos A B C

Potencia de un punto respecto de una circunferencia CP_5 P_04 Dadas tres circunferencias c 1, c 2 y c 3 y tres puntos A 1, A 2 y A 3, hallar una circunferencia c de forma que los ejes radicales de la circunferencia c con las c 1, c 2 y c 3 pasen, respectivamente por los A 1, A 2 y A 3. c 2 A 1 c 3 A 2

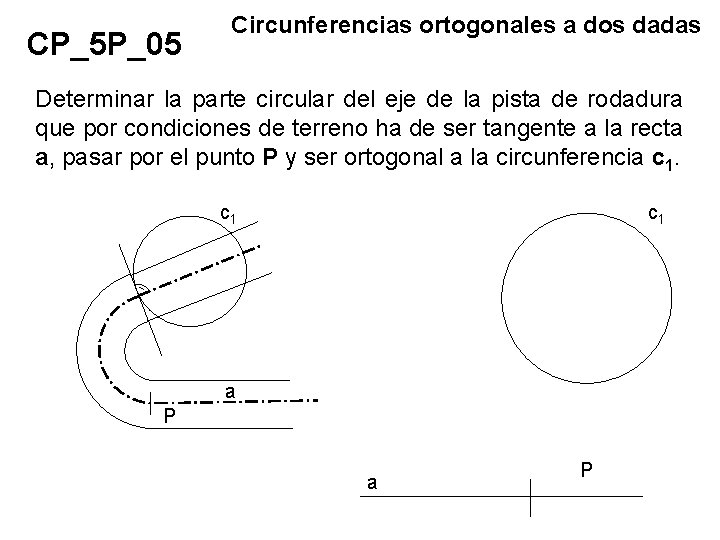
CP_5 P_05 Circunferencias ortogonales a dos dadas Determinar la parte circular del eje de la pista de rodadura que por condiciones de terreno ha de ser tangente a la recta a, pasar por el punto P y ser ortogonal a la circunferencia c 1 a P

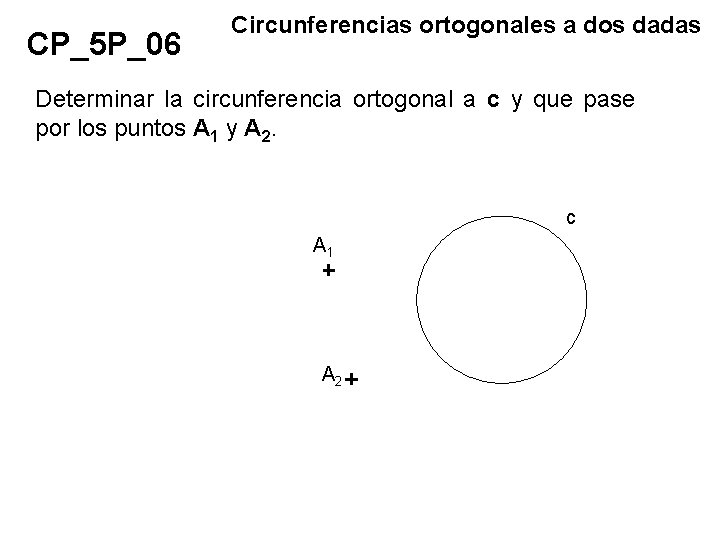
CP_5 P_06 Circunferencias ortogonales a dos dadas Determinar la circunferencia ortogonal a c y que pase por los puntos A 1 y A 2. c A 1 A 2