Covariance matrix for data and prediction points Mean

Covariance matrix for data and prediction points • Mean function (trend function) is often defined by a polynomial • Correlation of the covariance function determines the influences of the data on the prediction with uncertainty – The Gaussian covariance determines the influence by the square of the distance between two points and has two parameters, s and q – With the kernel, the covariance matrix of prediction point x and k data points is expressed as a matrix of (1+k) by (1+k): 1 Structural & Multidisciplinary Optimization Group

Prediction Using Gaussian Process (Kriging) • Recall the mean and variance of a conditional PDF – Based on the observation f at k sampling points, the true function value at x is obtained where – Using the mean function and the covariance function: Correlations between x and the data points Correlations between data points 2 Structural & Multidisciplinary Optimization Group

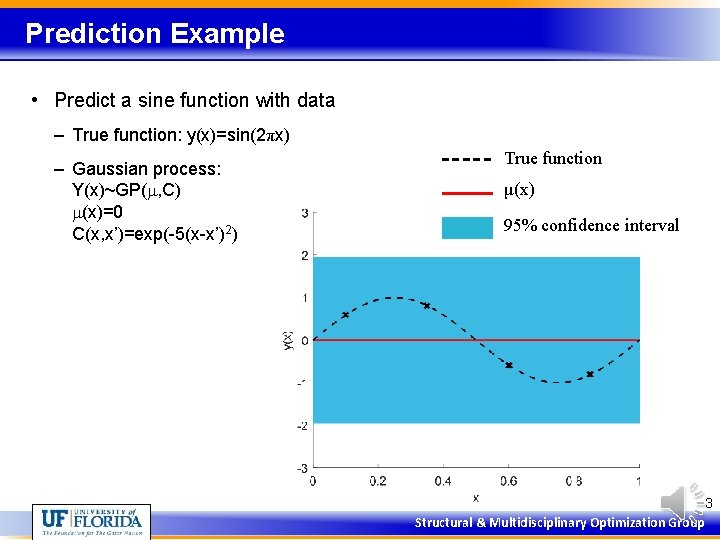
Prediction Example • Predict a sine function with data – True function: y(x)=sin(2πx) – Gaussian process: Y(x)~GP(m, C) m(x)=0 C(x, x’)=exp(-5(x-x’)2) True function μ(x) 95% confidence interval 3 Structural & Multidisciplinary Optimization Group

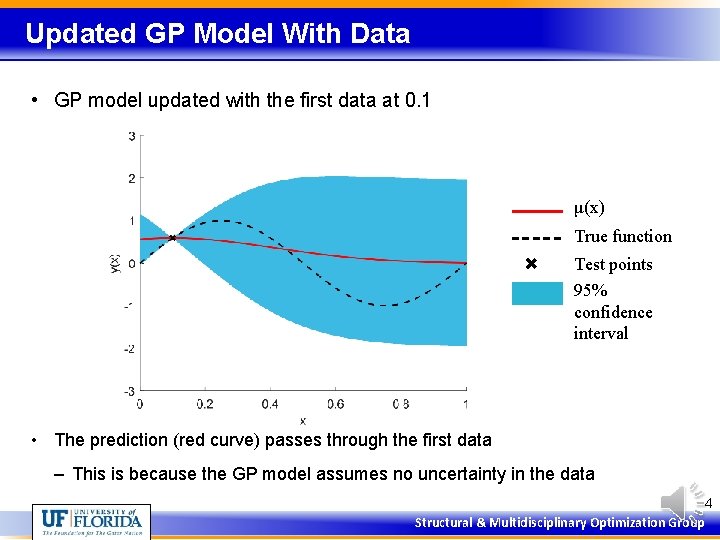
Updated GP Model With Data • GP model updated with the first data at 0. 1 μ(x) True function Test points 95% confidence interval • The prediction (red curve) passes through the first data – This is because the GP model assumes no uncertainty in the data 4 Structural & Multidisciplinary Optimization Group

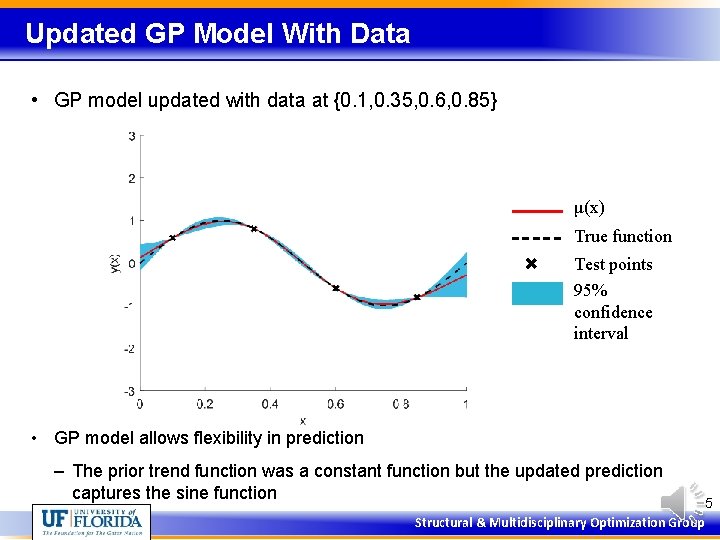
Updated GP Model With Data • GP model updated with data at {0. 1, 0. 35, 0. 6, 0. 85} μ(x) True function Test points 95% confidence interval • GP model allows flexibility in prediction – The prior trend function was a constant function but the updated prediction captures the sine function Structural & Multidisciplinary Optimization Group 5

My Notation •

Prediction and shape functions •

Fitting the data •

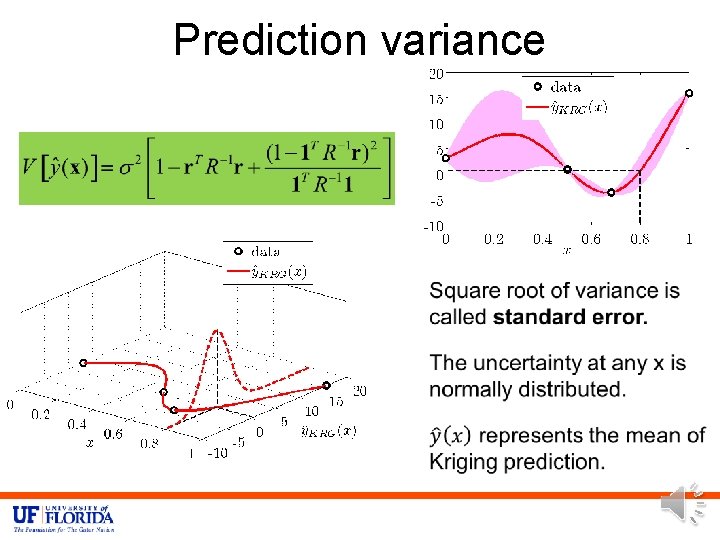
Prediction variance

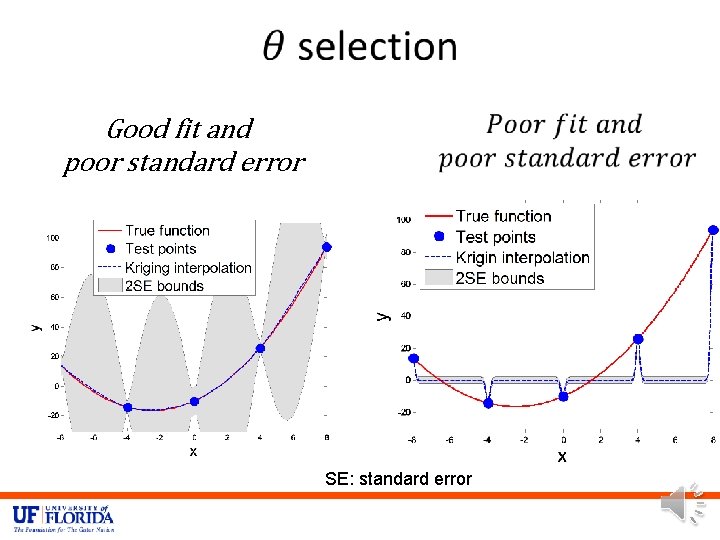
Kriging fitting issues • The maximum likelihood or cross-validation optimization problem solved to obtain the kriging fit is often illconditioned leading to poor fit, or poor estimate of the prediction variance. • Poor estimate of the prediction variance can be checked by comparing it to the cross validation error. • Poor fits are often characterized by the kriging surrogate having large curvature near data points (see example on next slide). • It is recommended to visualize by plotting the kriging fit and its standard error (for example between two data points).

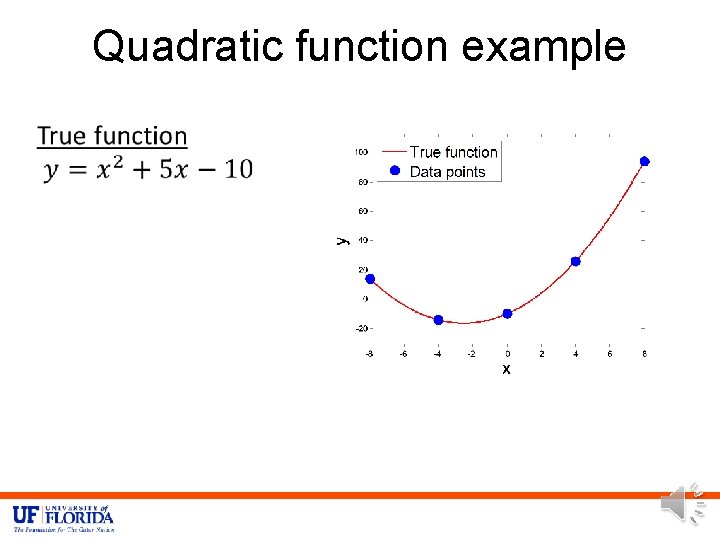
Quadratic function example

Good fit and poor standard error SE: standard error

Problems Kriging •