Course Syllabus 1 Introduction History Views Concepts Structure

Course Syllabus 1. Introduction - History; Views; Concepts; Structure 2. Process Management - Processes; State + Resources; Threads; Unix implementation of Processes 3. Process Scheduling – Paradigms; Unix; Modeling 4. Inter-Process Communication (IPC) 4. Process Synchronization - Synchronization primitives and their equivalence; Deadlocks 5. Memory Management - Virtual memory; Page replacement algorithms; Segmentation 6. File Systems - Implementation; Directory and space management; Unix file system; Distributed file systems (NFS) 7. Security – General policies and mechanisms; protection models; authentication 8. Distributed issues – Synchronization; Mutual exclusion Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 1

Inter-Process Communication (IPC) Processes need to communicate to exchange data and/or synchronize their work. § File: A record stored on a file that can be accessed by name the communicating processes. § Signal: A short system message sent from one process to another, not usually used to store information but instead give commands. § Message Exchange: An anonymous data stream that stores and retrieves information in packets. § Shared memory: Memory region shared by the communicating processes, which are allowed to read and change the content of the shared memory. Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 2

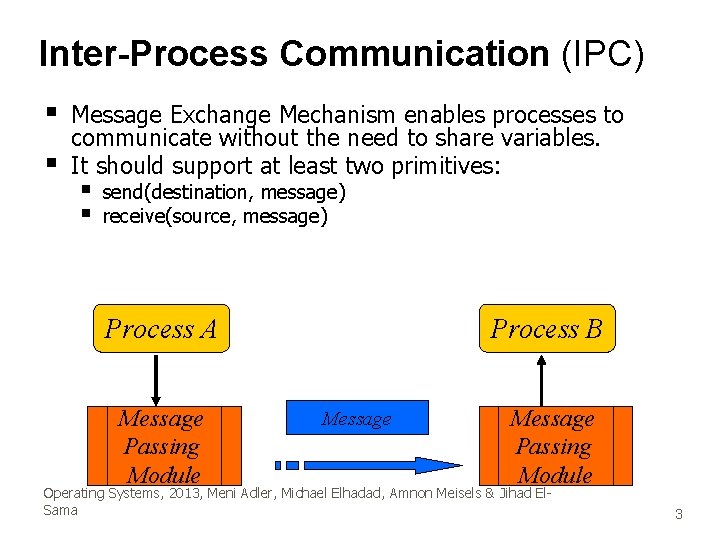
Inter-Process Communication (IPC) § § Message Exchange Mechanism enables processes to communicate without the need to share variables. It should support at least two primitives: § § send(destination, message) receive(source, message) Process A Message Passing Module Process B Message Passing Module Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 3

Message Format Message consists of § Header § Message Type § Source & Destination ID § Message Properties § Control Information Header Body Message Content § Body § The message data Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 4

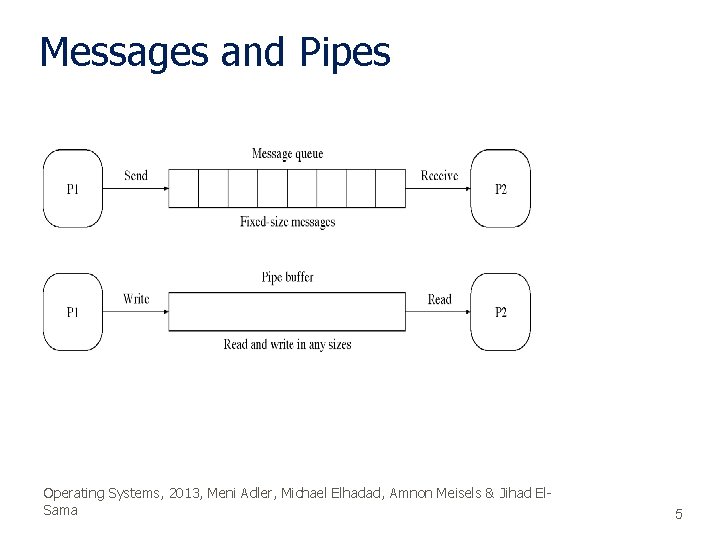
Messages and Pipes Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 5

Message Exchange Mechanism § A general method used for IPC: § Inside the same system/computer § In a networked/distributed system. § Message passing could be § Blocking(synchronous): § The sender blocks until the message is received § The receiver blocks until a message is available § Non-Blocking(asynchronous): § The sender sends the message and continue § The receiver receives a valid message or null Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 6

Message Passing Synchronization § The sender § Sends message to multiple destination § Usually expects acknowledgement § The Receiver § Need the received information to proceed § It could be blocked indefinitely if the sender failed or the message was not received. Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 7

Send-Received Synchronization The three practical combination: § Blocking send, blocking receive § Non-blocking send, Non-blocking receive § Non-blocking send, Blocking receive Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 8

Queue of messages § Order § Usually FIFO § Capacity § Zero: Sender must wait for receiver § Bounder (predefined length): send wait if the queue is full § Unbounded: sender never waits Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 9

Direct verse Indirect § Direct § Processes identifier is used for source and destination. § Indirect § Messages are sent to shared mailbox § The receiver picked up the messages from the mailbox § The message are queued within the mailbox Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El. Sama 10

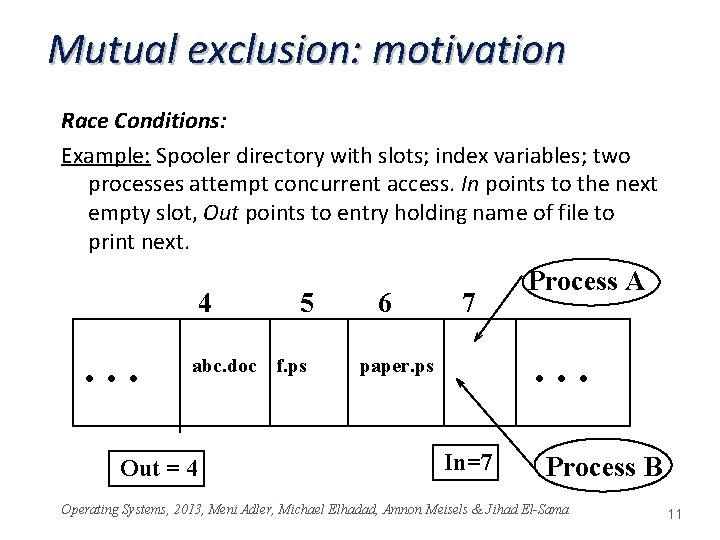
Mutual exclusion: motivation Race Conditions: Example: Spooler directory with slots; index variables; two processes attempt concurrent access. In points to the next empty slot, Out points to entry holding name of file to print next. 4 . . . 5 abc. doc f. ps Out = 4 6 7 Process A . . . paper. ps In=7 Process B Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 11

Code using reads/writes only Add_file_to_print_spool (char *name) 1. Local_in : = In 2. Store. Name(Spool_dir[local_in], name) 3. In : = (local_in+1) mod DIR_LEN A scenario proving the above code wrong • Process A performs line 1 • Process A is preempted by Process B • Process B performs Add_file_to_print_spool to completion • Process A is re-scheduled, completes lines 2 -3. Process B's file is never printed. Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 12

The mutual exclusion problem (Dijkstra, 1965) How can we avoid such race conditions? We need to devise a protocol that guarantees mutually exclusive access by processes to a shared resource (such as a file, printer, etc. ) or, more generally, a critical section of code Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 13

The problem model q Multiple processes q Processes can apply read, write, or stronger operations to shared memory q Completely asynchronous q We assume processes do not fail-stop Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 14

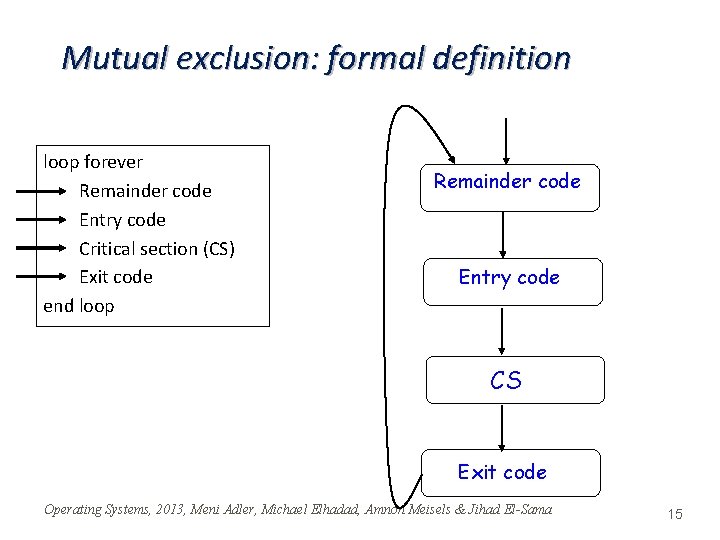
Mutual exclusion: formal definition loop forever Remainder code Entry code Critical section (CS) Exit code end loop Remainder code Entry code CS Exit code Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 15

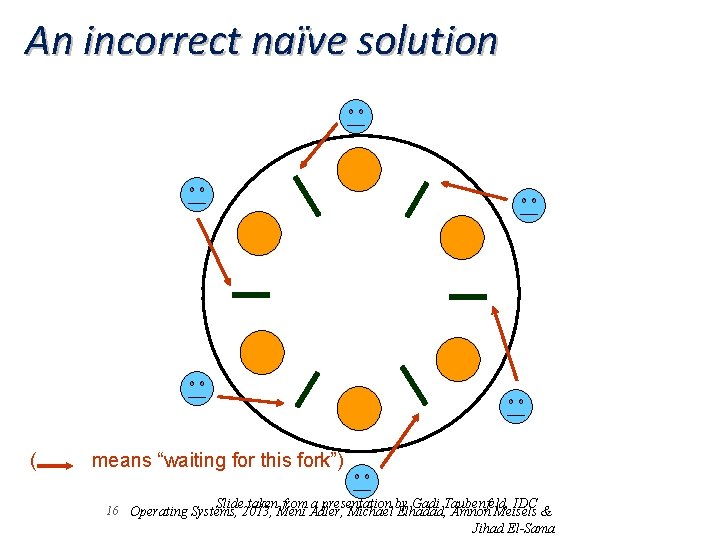
An incorrect naïve solution ( means “waiting for this fork”) Slide taken from a presentation by Gadi Taubenfeld, IDC 16 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

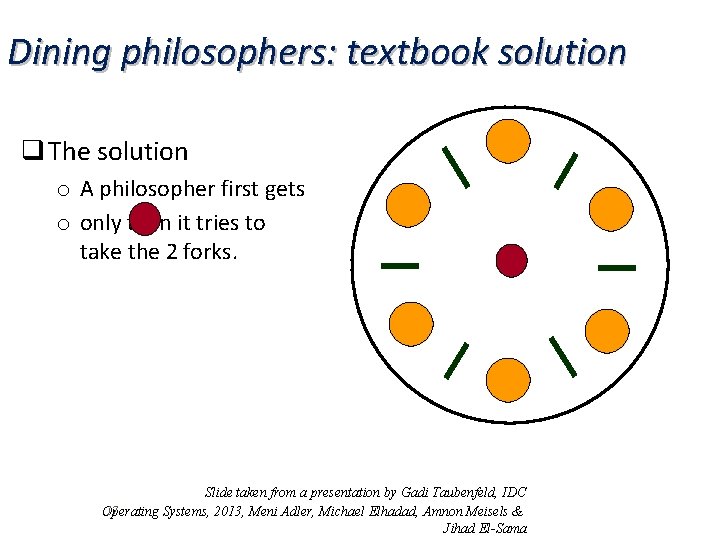
Dining philosophers: textbook solution q The solution o A philosopher first gets o only then it tries to take the 2 forks. Slide taken from a presentation by Gadi Taubenfeld, IDC 17 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

Dining philosophers: textbook solution code #define N 5 #define THINKING #define HUNGRY #define EATING 0 1 2 int state[N]; semaphore mutex = 1; semaphore s[N]; // per each philosopher int left(int i) { return (i-1) % N; } int right(in it) { return (i+1) % N; } void philosopher(int i) { while (TRUE) { think(); pick_sticks(i); eat(); put_sticks(i); } } 18 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

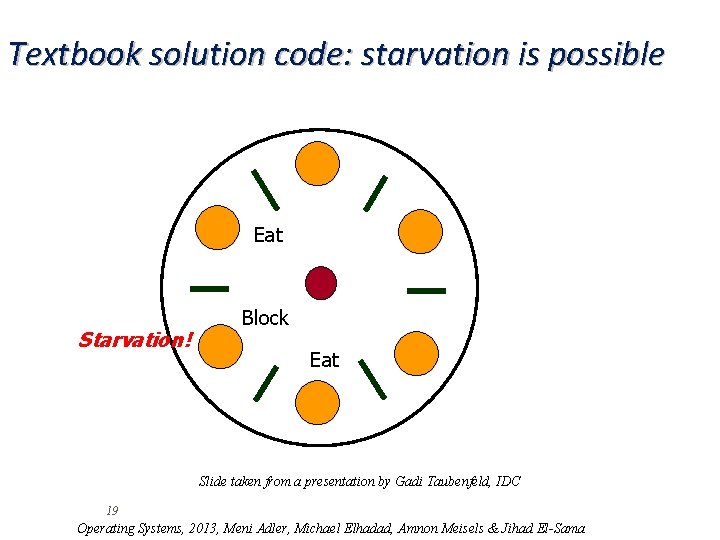
Textbook solution code: starvation is possible Eat Starvation! Block Eat Slide taken from a presentation by Gadi Taubenfeld, IDC 19 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

Textbook solution disadvantages q An inefficient solution o reduces to mutual exclusion o not enough concurrency o Starvation possible 20 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

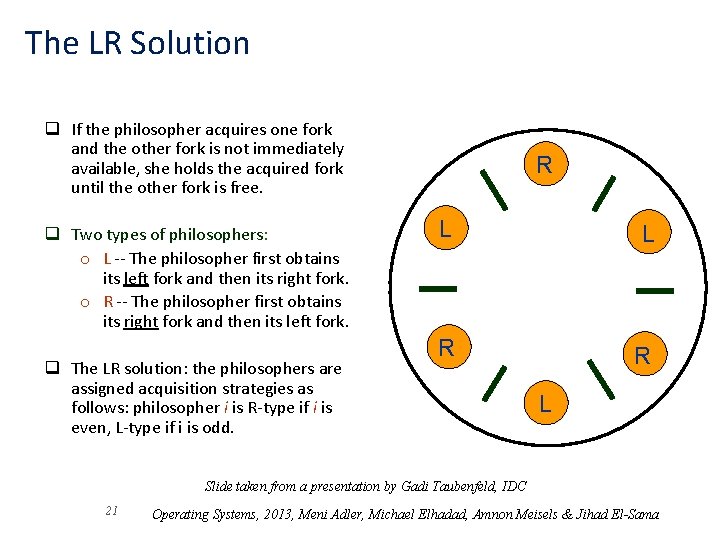
The LR Solution q If the philosopher acquires one fork and the other fork is not immediately available, she holds the acquired fork until the other fork is free. q Two types of philosophers: o L -- The philosopher first obtains its left fork and then its right fork. o R -- The philosopher first obtains its right fork and then its left fork. q The LR solution: the philosophers are assigned acquisition strategies as follows: philosopher i is R-type if i is even, L-type if i is odd. R L L R R L Slide taken from a presentation by Gadi Taubenfeld, IDC 21 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

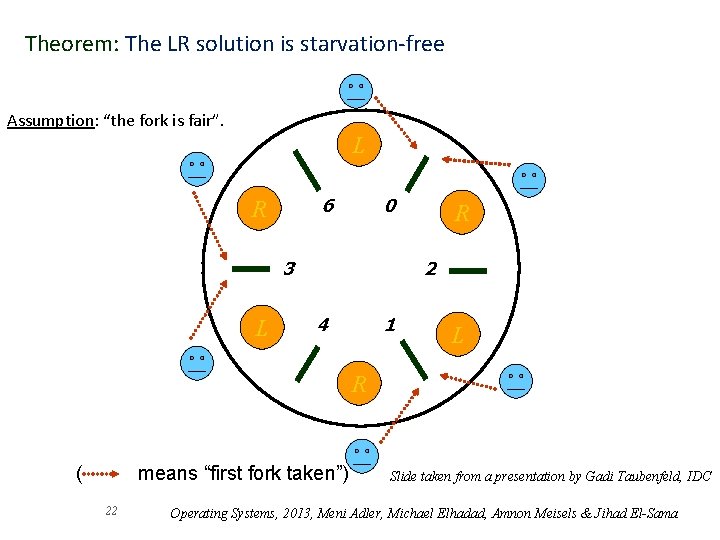
Theorem: The LR solution is starvation-free Assumption: “the fork is fair”. L 6 R 0 3 L R 2 4 1 L R ( means “first fork taken”) 22 Slide taken from a presentation by Gadi Taubenfeld, IDC Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama

Mutex Requirements q Mutual exclusion: No two processes are at the critical section (CS) at the same time q Deadlock-freedom: If processes are trying to enter their critical section, then some process eventually enters the critical section q Starvation-freedom: If a process is trying to enter its critical section, then this process must eventually enter its critical section Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 23

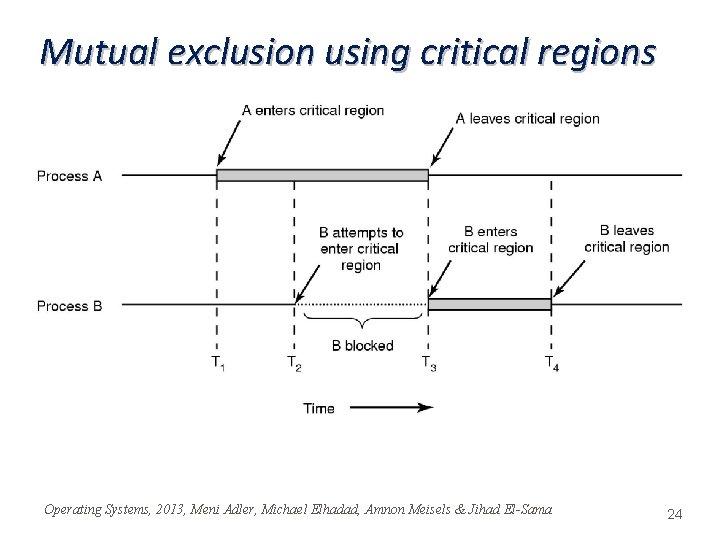
Mutual exclusion using critical regions Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 24

Brute force solution: disabling interrupts Disable interrupts Do your stuff Enable interrupts Problems q User processes are not allowed to disable interrupts q Disabling interrupts must be done for a very short period of time q Does not solve the problem in a multi-processor system Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 25

2 -process Mutual Exclusion with a lock variable initially: lock=0 Program for both processes 1. 2. 3. 4. await lock=0 lock: =1 CS lock: =0 No Does it satisfy deadlock-freedom? Yes Does it satisfy starvation-freedom? No Does the algorithm satisfy mutex? Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 26

Mutual Exclusion: strict alternation initially: turn=0 Program for process 0 1. 2. 3. await turn=0 CS turn: =1 Program for process 1 1. 2. 3. await turn=1 CS turn: =0 Yes Does it satisfy deadlock-freedom? No Does it satisfy starvation-freedom? No Does the algorithm satisfy mutex? Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 27

Mutual Exclusion: flag array bool flags[2] initially {false, false} Program for process 0 1. 2. 3. 4. flags[0]: =true await flags[1]=false CS flags[0]: =false Program for process 1 1. 2. 3. 4. flags[1]: =true await flags[0]=false CS flags[1]: =false Yes Does it satisfy deadlock-freedom? No Does it satisfy starvation-freedom? No Does the algorithm satisfy mutex? Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 28

Peterson’s 2 -process algorithm (Peterson, 1981) initially: b[0]: =false, b[1]: =false, value of turn immaterial Program for process 0 Program for process 1 1. 2. 3. 4. 5. b[0]: =true turn: =0 await (b[1]=false or turn=1) CS b[0]: =false b[1]: =true turn: =1 await (b[0]=false or turn=0) CS b[1]: =false Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 29

Schema for Peterson’s 2 -process algorithm Indicate participation b[i]: =true Barrier turn: =i Is there contention? b[1 -i]=true? no Critical Section no, maybe yes First to cross barrier? turn=1 -i? yes Exit code b[i]: =false Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 30

Peterson’s 2 -process algorithm satisfies both mutual-exclusion and starvation-freedom Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 31

Observations v Shared register: turn (2 -valued) read & write by both processes v Two boolean registers: b[0], b[1] process 0 can write b[0], process 1 can write b[1] both can read b[0] & b[1] Can the algorithm be modified to use only single-writer registers ? Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 32

Kessels’ 2 -process algorithm (1982) encode turn=0: as turn[0] = turn[1] turn=1: as turn[0] ≠ turn[1] initially: b[0]: =false, b[1]: =false, value of turn[i] immaterial Program for process 0 Program for process 1 1. 2. 3. 4. 5. 6. b[0]: =true local[0]: =turn[1] turn[0]: =local[0] await (b[1]=false or local[0] ≠ turn[1]) CS b[0]: =false 5. 6. b[1]: =true local[1]: =1 – turn[0] turn[1]: =local[1] await (b[0]=false or local[1] = turn[0]) CS b[1]: =false Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 33

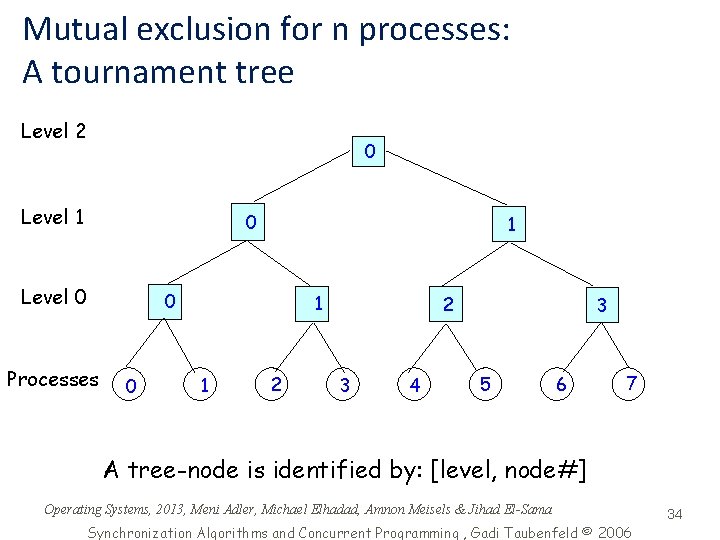
Mutual exclusion for n processes: A tournament tree Level 2 0 Level 1 0 Level 0 1 0 Processes 0 1 1 2 2 3 4 3 5 6 7 A tree-node is identified by: [level, node#] Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 34

N-process mutual exclusion: a tournament tree Variables Per node: b[level, 2 node], b[level, 2 node+1], turn[level, node] Per process (local): level, node, id. Program for process i 1. node: =i 2. For level = 0 to log n-1 do 3. id: =node mod 2 4. node: = node/2 5. b[level, 2 node+id]: =true 6. turn[level, node]: =id 7. await (b[level, 2 node+1 -id]=false or turn[level, node]=1 -id) 8. od 9. CS 10. for level=log n – 1 downto 0 do 11. node: = i/2 level 12. b[level, node]: =false Operating Systems, 13. 2013, od Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 35

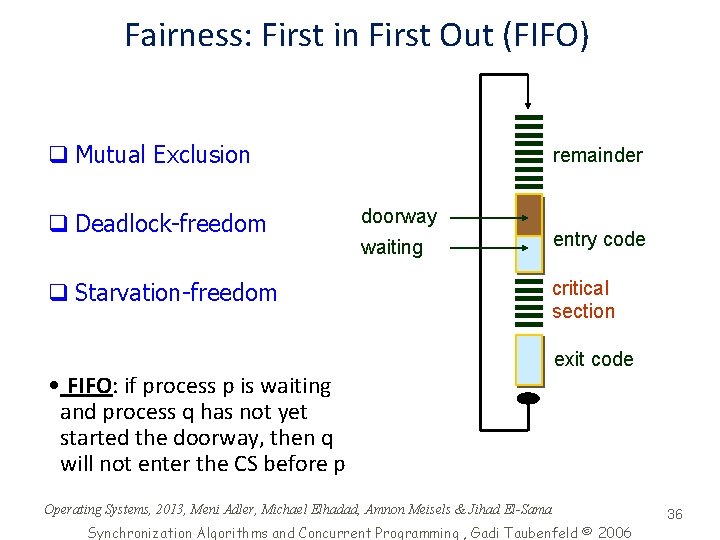
Fairness: First in First Out (FIFO) q Mutual Exclusion q Deadlock-freedom remainder doorway waiting q Starvation-freedom • FIFO: if process p is waiting and process q has not yet started the doorway, then q will not enter the CS before p entry code critical section exit code Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 36

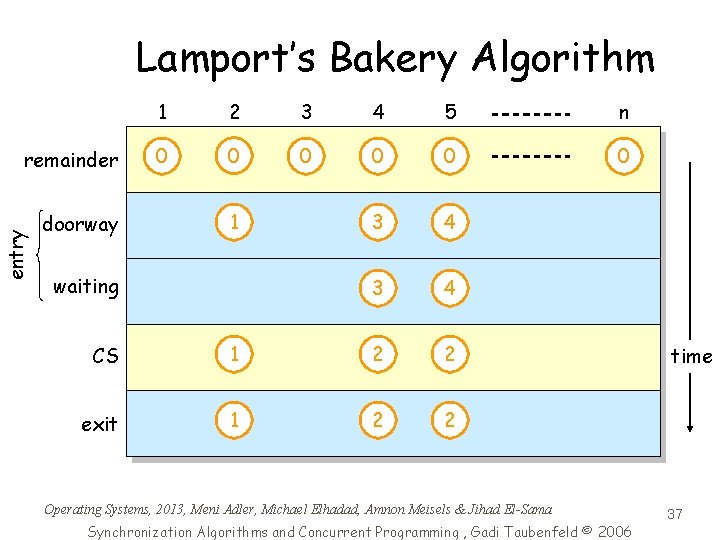
Lamport’s Bakery Algorithm entry remainder 1 2 3 4 5 n 0 0 0 doorway 1 2 3 2 4 waiting 1 2 3 2 4 CS 1 2 2 exit 1 2 2 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 time 37

Implementation 1 code of process i , i {1 , . . . , n} number[i] : = 1 + max {number[j] | (1 j n)} for j : = 1 to n (<> i) { await (number[j] = 0) (number[j] > number[i]) } critical section number[i] : = 0 number 1 2 3 4 0 0 n 0 0 integer Does this implementation work? Answer: No, it can deadlock! Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 38

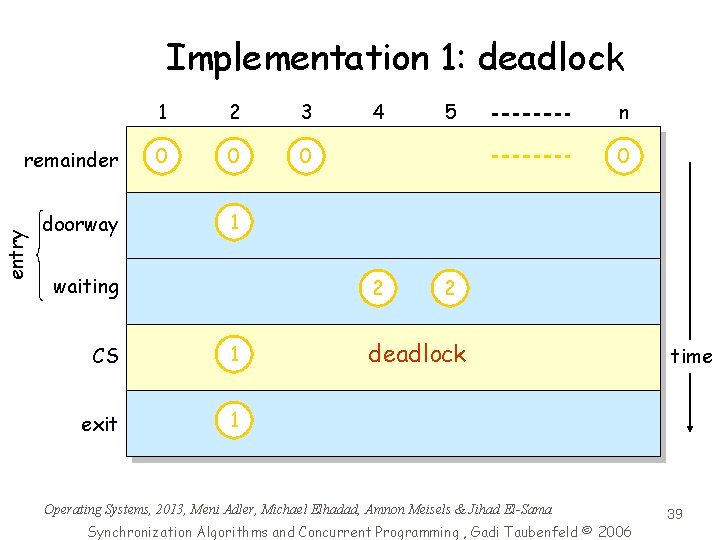
Implementation 1: deadlock entry remainder 1 2 3 4 5 n 0 0 0 doorway 1 2 2 waiting 1 2 2 CS 1 deadlock exit 1 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 time 39

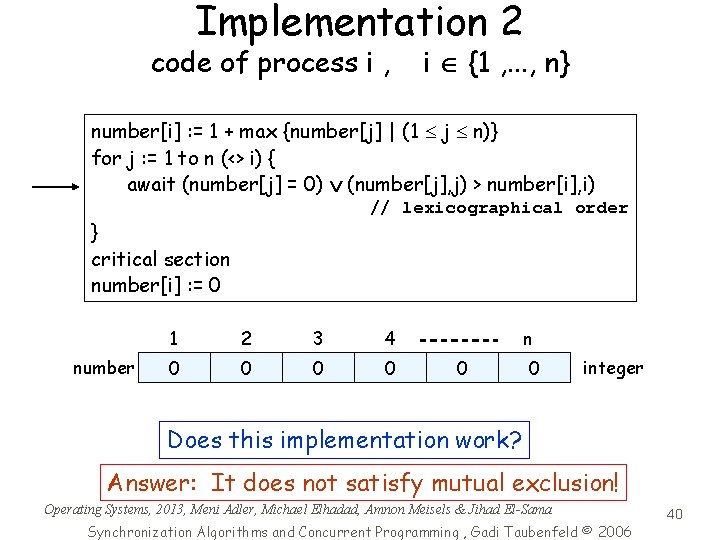
Implementation 2 code of process i , i {1 , . . . , n} number[i] : = 1 + max {number[j] | (1 j n)} for j : = 1 to n (<> i) { await (number[j] = 0) (number[j], j) > number[i], i) // lexicographical order } critical section number[i] : = 0 number 1 2 3 4 0 0 n 0 0 integer Does this implementation work? Answer: It does not satisfy mutual exclusion! Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 40

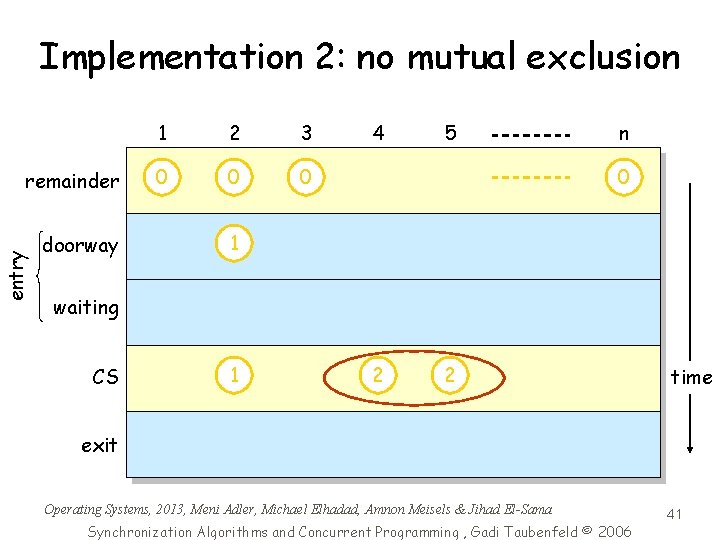
Implementation 2: no mutual exclusion entry remainder 1 2 3 4 5 n 0 0 0 doorway 0 1 0 2 waiting 1 2 2 CS 1 2 2 exit 1 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama Synchronization Algorithms and Concurrent Programming , Gadi Taubenfeld © 2006 time 41

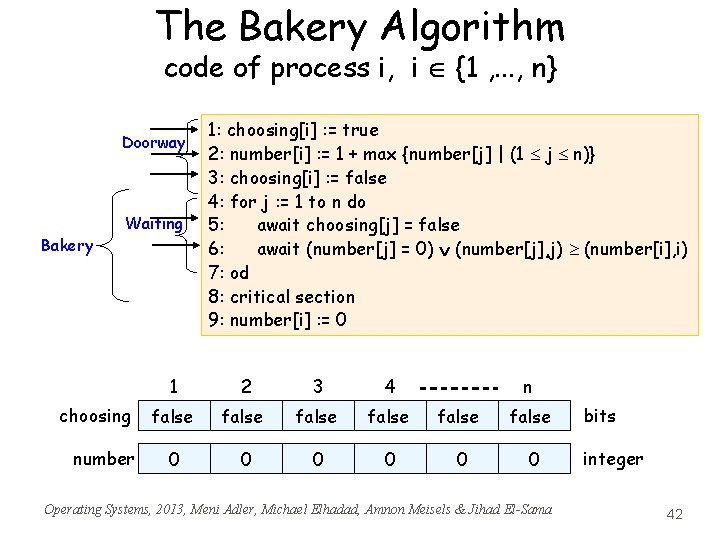
The Bakery Algorithm code of process i, i {1 , . . . , n} Doorway Bakery Waiting choosing number 1: choosing[i] : = true 2: number[i] : = 1 + max {number[j] | (1 j n)} 3: choosing[i] : = false 4: for j : = 1 to n do 5: await choosing[j] = false 6: await (number[j] = 0) (number[j], j) (number[i], i) 7: od 8: critical section 9: number[i] : = 0 1 2 3 4 n false false 0 0 0 Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama bits integer 42

Lamport’s bakery algorithm satisfies mutual-exclusion, starvation-freedom, and FIFO Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 43

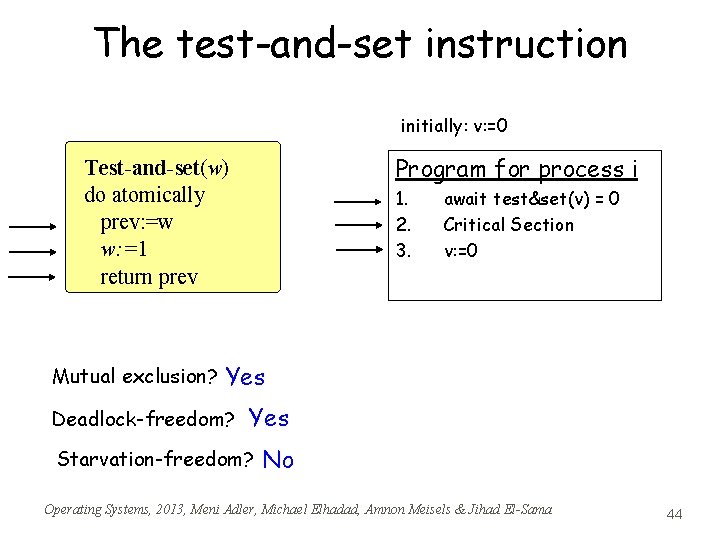
The test-and-set instruction initially: v: =0 Program for process i Test-and-set(w) do atomically prev: =w w: =1 return prev Mutual exclusion? 1. 2. 3. await test&set(v) = 0 Critical Section v: =0 Yes Deadlock-freedom? Yes Starvation-freedom? No Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 44

Starvation-free mutex using test-and-set boolean lock initially 0, interested[n] initially false program for process i 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. interested[i]: =true await ( (test-and-set(lock) = 0) || (interested[i]=false) ) CS interested[i]: =false j: =(i+1) % n while (j != i && !interested[j]) j: =++j % n if (j=i) lock: =0 else interested[j]: =false Operating Systems, 2013, Meni Adler, Michael Elhadad, Amnon Meisels & Jihad El-Sama 45