Course Review Part 3 Manual stability control Manual

Course Review Part 3

• Manual stability control • Manual servo control

6. 6 Reset windup • The condition where the integral action drives the controller output to one of its limits. • Usually because of – Poor configuration – Undersized (or oversized) valve • The controller cannot reach setpoint - offset. This offset causes the integral term to wind up • The controller may be slow in responding to a change in the controlled variable because of the dominant integral term
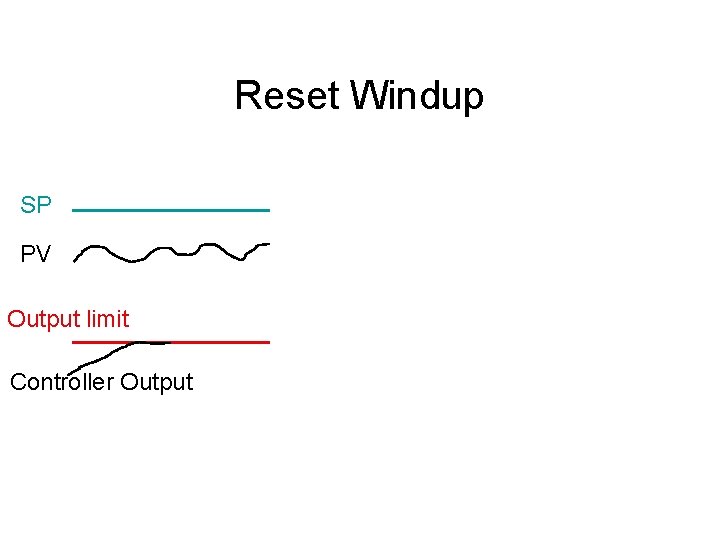
Reset Windup SP PV Output limit Controller Output
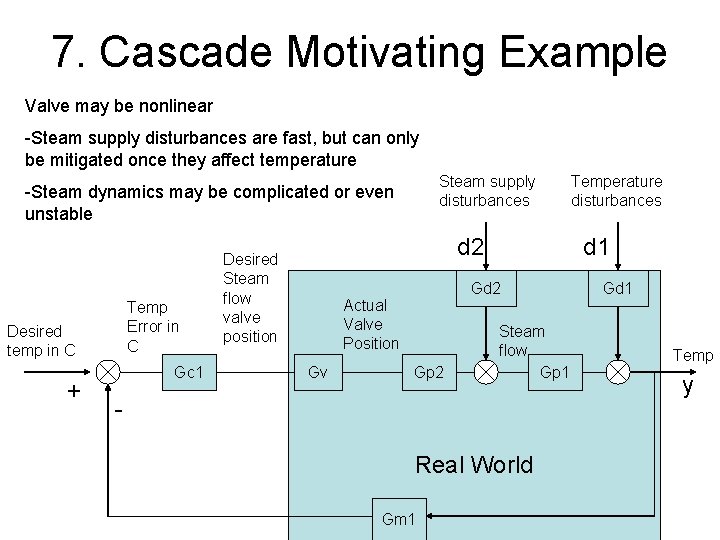
7. Cascade Motivating Example Valve may be nonlinear -Steam supply disturbances are fast, but can only be mitigated once they affect temperature Steam supply disturbances -Steam dynamics may be complicated or even unstable Temp Error in C Desired temp in C + Gc 1 d 2 Desired Steam flow valve position Gv d 1 Gd 2 Actual Valve Position Gp 2 Steam flow Gp 1 Real World Gm 1 Temperature disturbances Gd 1 Temp y
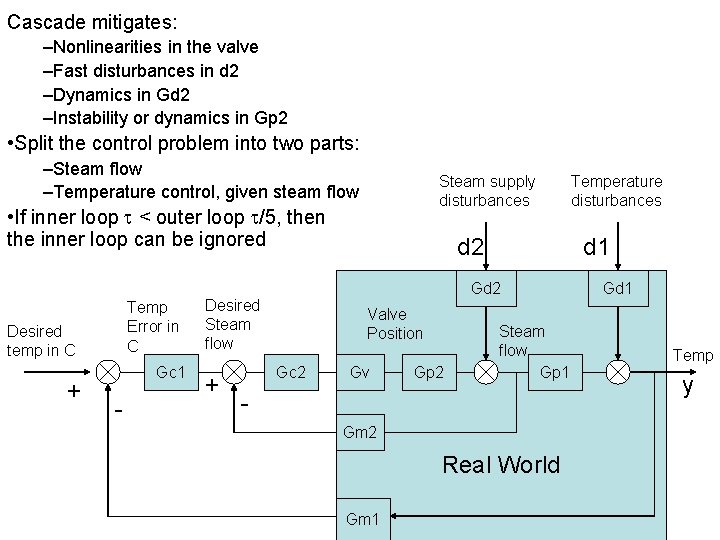
Cascade mitigates: –Nonlinearities in the valve –Fast disturbances in d 2 –Dynamics in Gd 2 –Instability or dynamics in Gp 2 • Split the control problem into two parts: –Steam flow –Temperature control, given steam flow Steam supply disturbances • If inner loop < outer loop /5, then the inner loop can be ignored Temp Error in C Desired temp in C + Gc 1 - d 1 Gd 2 Desired Steam flow + d 2 Valve Position Gc 2 Gv Gp 2 Steam flow Gp 1 Gm 2 Real World Gm 1 Temperature disturbances Gd 1 Temp y

8. Feedforward • Feedback is mostly about the poles of the transfer function: long term behaviour and stability • Feedforward is about the zeros of the transfer function: short term dynamics • Feedback cannot affect the zeros of a transfer function. Feedforward can. • Can be very useful if there is a long time delay in Gd and Gp.
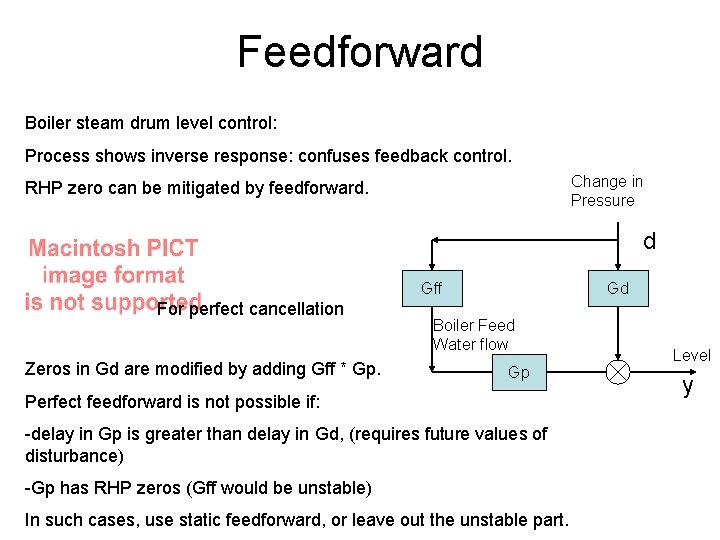
Feedforward Boiler steam drum level control: Process shows inverse response: confuses feedback control. Change in Pressure RHP zero can be mitigated by feedforward. d Gff For perfect cancellation Zeros in Gd are modified by adding Gff * Gp. Gd Boiler Feed Water flow Gp Perfect feedforward is not possible if: -delay in Gp is greater than delay in Gd, (requires future values of disturbance) -Gp has RHP zeros (Gff would be unstable) In such cases, use static feedforward, or leave out the unstable part. Level y

9. Routh Stability Criterion Useful to find limiting values of Kc and I Can only be used on polynomials • • – 1. If characteristic equation contains exponentials, use a Pade approximation Write characteristic equation as a polynomial: Make coefficient of highest power of s (an) positive If any coefficient is negative or zero, system is not stable 2. If all coefficients are positive, construct Routh array:
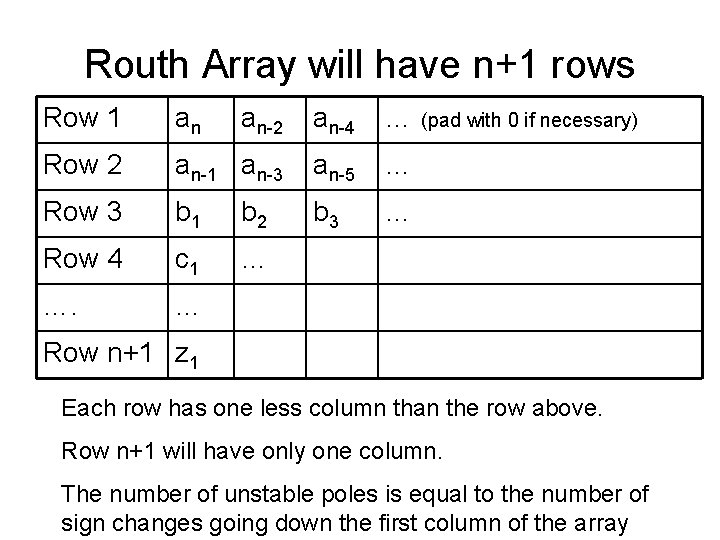
Routh Array will have n+1 rows Row 1 an an-2 an-4 … (pad with 0 if necessary) Row 2 an-1 an-3 an-5 … Row 3 b 1 b 2 b 3 … Row 4 c 1 … …. … Row n+1 z 1 Each row has one less column than the row above. Row n+1 will have only one column. The number of unstable poles is equal to the number of sign changes going down the first column of the array

Calculation

10. Frequency Response

Amplitude Ratio and Phase Shift using Transfer Functions 1. 2. 3. 4. Replace S with j in the transfer function: G(s) G(j ) Rationalize G: make it equal to a + jb, where a and b may be functions of (G is now a complex number that is a function of ) AR = |G| = sqrt(a 2 + b 2) = tan-1(b/a)
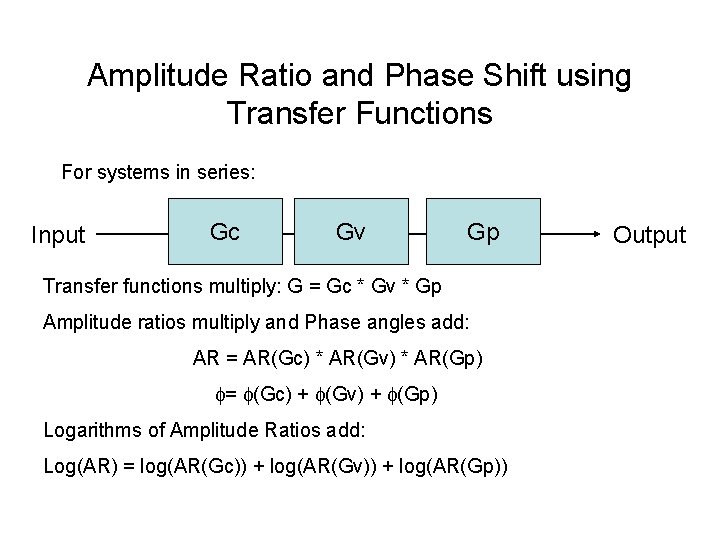
Amplitude Ratio and Phase Shift using Transfer Functions For systems in series: Input Gc Gv Gp Transfer functions multiply: G = Gc * Gv * Gp Amplitude ratios multiply and Phase angles add: AR = AR(Gc) * AR(Gv) * AR(Gp) = (Gc) + (Gv) + (Gp) Logarithms of Amplitude Ratios add: Log(AR) = log(AR(Gc)) + log(AR(Gv)) + log(AR(Gp)) Output
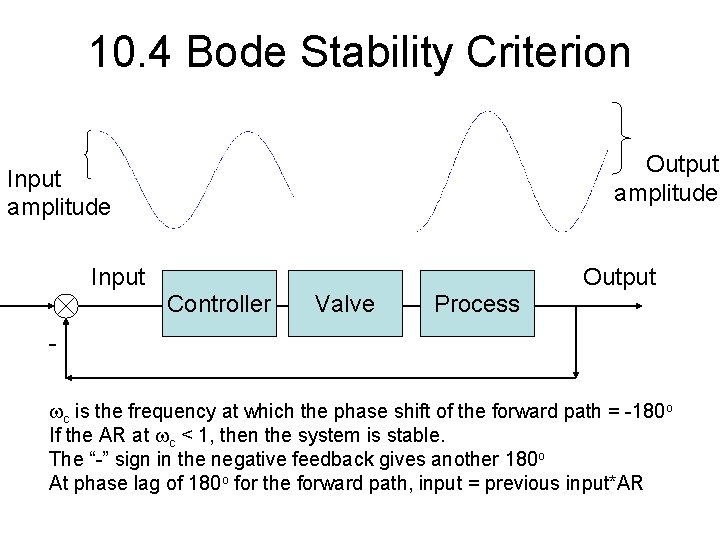
10. 4 Bode Stability Criterion Output amplitude Input Output Controller Valve Process c is the frequency at which the phase shift of the forward path = -180 o If the AR at c < 1, then the system is stable. The “-” sign in the negative feedback gives another 180 o At phase lag of 180 o for the forward path, input = previous input*AR
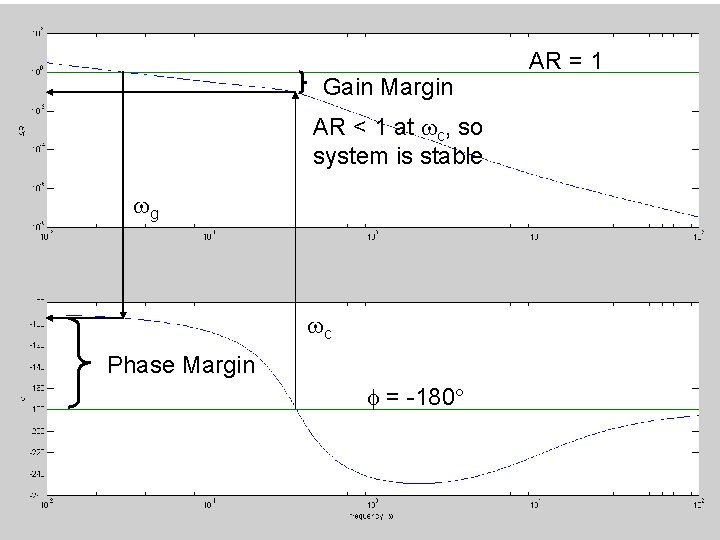
AR = 1 10. 4 Bode Stability Criterion, Gain Margin < 1 at , Margin so Gain and AR Phase c system is stable g c Phase Margin = -180

11. Multivariable Systems

Break

Feedback • Control of unstable system
- Slides: 19