Course Review Distributions What are the important aspects

Course Review

Distributions • What are the important aspects needed to describe a distribution of one variable? • List three types of graphs that could be used to display a one-variable distribution. • Name two easy ways to check if a distribution is approximately normal. • In a skewed distribution, how does median relate to mean?

Regression • • • When would you use linear regression? What is r? What values can it take on? What does r 2 tell you? What is the meaning of a? What is the meaning of b? What important technique gives evidence that a linear model is appropriate? • What IS a residual? • What are the two important non-linear models we studied? How could you guess which is appropriate in a particular situation? • For the those non-linear models we studied, how do you linearize the data and get the mathematical model?

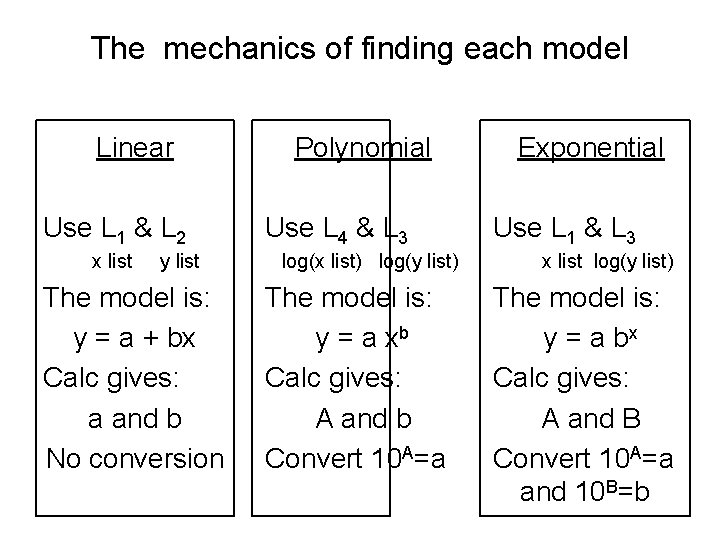
The mechanics of finding each model Linear Use L 1 & L 2 x list y list The model is: y = a + bx Calc gives: a and b No conversion Polynomial Use L 4 & L 3 log(x list) log(y list) The model is: y = a xb Calc gives: A and b Convert 10 A=a Exponential Use L 1 & L 3 x list log(y list) The model is: y = a bx Calc gives: A and B Convert 10 A=a and 10 B=b

Experiments and Studies • What is the difference between a study and an experiment? • Define a probability sample. • What are three elements that MUST be present in any experiment? • What does double-blind mean? • What are the five steps of a simulation?

Probability • Write a definition of probability. • What is a sample space? • What is the sum of probabilities in the sample space? • What are independent events? • What are disjoint events? • Write the full OR probability formula. • Write the full AND probability formula.

Random Variables • What is a discrete random variable? • How is it different from a continuous r. v. ? • What is a p. d. f. ? A c. d. f. ? How are they displayed? • How is a continuous r. v. displayed? • What is the expected value of a discrete random variable? • What is the binomial setting? • What is the geometric setting?

Inference • What is a sampling distribution? • Describe the sampling distribution for sample means if X is N(μ, σ). • Describe the sampling distribution for sample proportions if the population proportion is p. • Describe the logic of hypothesis testing. • Describe the meaning of a C% confidence interval.

Assumptions • What must be true for hypothesis tests and confidence intervals for means? • What must be true for hypothesis tests and confidence intervals for proportions? • What must be true for hypothesis tests for distributions? • What must be true for hypothesis tests for linear regression?

Assumptions Summary Assumptions Procedure • • • One population t for means Two population t for means One population z for proportions Two population z for proportions X 2 test for distributions • • • SRS, Normal Dist SRS, Normal, Independent SRS, large pop, 10 succ/fail SRS, large pop, 5 s/f each SRS, expect each count at least 1 – No more than 20% less than 5 • t procedures for linear regression • SRS, Association is linear; response variable varies normally about the LSRL with constant standard deviation.

5 Steps to Score a 4! 1. State the procedure appropriate to the problem • • 2. 2 -population t-test for means 1 -population z interval for proportions Chi-squared test for distributions etc! State the assumptions needed for the test and verify that they are met State hypotheses and significance level Perform the calculation; state the test statistic value and the p-value 3. 4. • • Formula: show all work Calculator: state screen used and results • 5. Explicitly state the statistic (z or t or X 2) and p value State your conclusion in the context of the problem 1. Remember the 3 -phrase form for tests or intervals