Course Outline Traditional Static Program Analysis Class analyses

Course Outline • Traditional Static Program Analysis – Class analyses – Call graphs • Software Testing, Refactoring • Dynamic Program Analysis

Announcements • The new page for the class is at www. rpi. edu/~milana 2/csci 6961 • Email: milana 2@rpi. edu , milanova@cs. rpi. edu • All, send me an email with your CS login

Outline • Analysis of object references – Class Hierarchy Analysis (CHA) – Rapid Type Analysis (RTA) • Call graphs

Analysis of object references • Analysis of object-oriented programs – Java • Class Analysis problem: Given a reference variable x, what are the classes of the objects that x refers to at runtime? • Points-to Analysis problem: Given a reference variable x, what are the objects that x refers to at runtime?

Java Example: Bool. Exp hierarchy public class And. Exp extends Bool. Exp { private Bool. Exp _operand 1; private Bool. Exp _operand 2; public And. Exp(Bool. Exp op 1, Bool. Exp op 2) { _operand=op 1; _operand 2=op 2; } public boolean Evaluate(Context c) { return _operand 1. Evaluate(c) && _operand 2. Evaluate(c); } } _operand 1: {Constant} _operand 2: {Or. Exp} public class Or. Exp extends Bool. Exp { private Bool. Exp _operand 1; private Bool. Exp _operand 2; public Or. Exp(Bool. Exp op 1, Bool. Exp op 2) { _operand=op 1; _operand 2=op 2; } public boolean Evaluate(Context c) { return _operand 1. Evaluate(c) || _operand 2. Evaluate(c); } } _operand 1: {Var. Exp} _operand 2: {Var. Exp}

Class information: applications • Compilers: can we devirtualize a virtual function call x. m()/x->m()? • Software engineering – The calling relations in the program: call graph – Testing – Most interesting analyses require this information

Some terminology • Intraprocedural analysis – So far, we assumed there are no procedure calls! – Analysis that works within a procedure and approximates (or does not need) flow into and from procedures • Interprocedural analysis – Takes into account procedure calls and tracks flow into and from procedures – Many issues: • • Parameter passing mechanisms Context Call graph! Functions as parameters! – We will get back to this in a few classes…

Scalability • For most analyses (including class analysis) we need interprocedural analysis on very large programs • Can the analysis handle large programs? – 100 K LOC, up to 45 M LOC? • Approximations of standard fixed point iteration – – Reduce Lattice Reduce CFG Make transfer functions converge faster Other…

Today’s class • Class analysis: Given a reference variable x, what are the classes of the objects that x refers to at runtime? • Class Hierarchy Analysis (CHA) • Rapid Type Analysis (RTA) • Call graphs

Class Hierarchy Analysis (CHA) • The simplest method of inferring information about reference variables – Look at the class hierarchy • In Java, if a reference variable r has a type A, the possible classes of run-time objects are included in the subtree of A. Denoted by cone(A). – At virtual call site r. m find the methods that may be called based on the hierarchy information J. Dean, D. Grove, and C. Chambers, Optimization of OO Programs Using Static Class Hierarchy Analysis, ECOOP’ 95

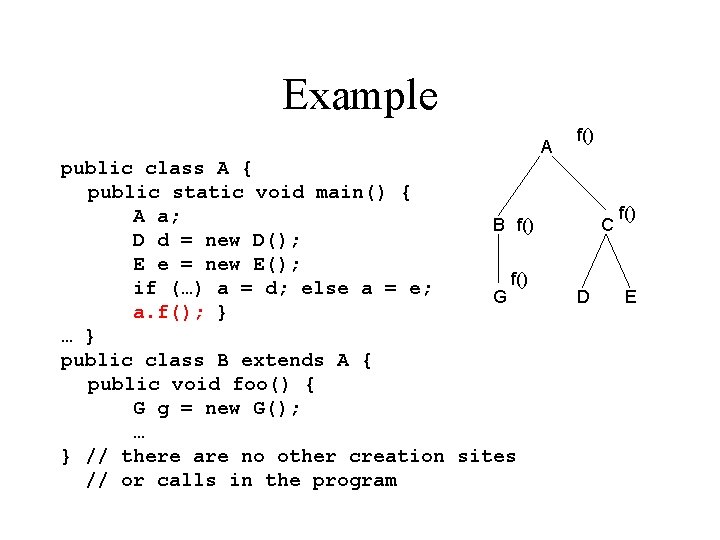
Example A public class A { public static void main() { A a; B f() D d = new D(); E e = new E(); f() if (…) a = d; else a = e; G a. f(); } … } public class B extends A { public void foo() { G g = new G(); … } // there are no other creation sites // or calls in the program f() C D f() E

Example A B f() G f() public class A { public static void main() { A a; f() D d = new D(); C E e = new E(); Cone(C) if (…) a = d; else a = e; a. f(); } D E … } public class B extends A { public void foo() { G g = new G(); … } // there are no other creation sites // or calls in the program The solution for reference variables by CHA is: a may refer to objects of classes {A, B, C, D, E, G}, d may refer to objects of class {D}, e may refer to objects of class {E}, and g to {G}.

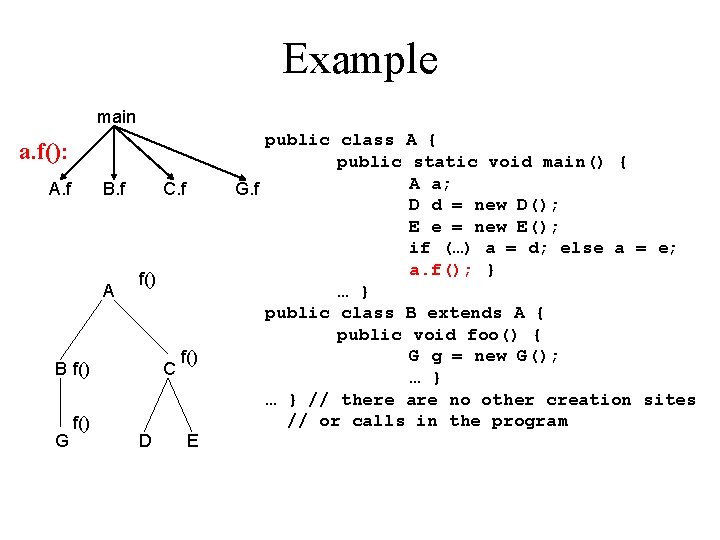
Example main a. f(): A. f B. f A C. f f() B f() G f() C D f() E public class A { public static void main() { A a; G. f D d = new D(); E e = new E(); if (…) a = d; else a = e; a. f(); } … } public class B extends A { public void foo() { G g = new G(); … } // there are no other creation sites // or calls in the program

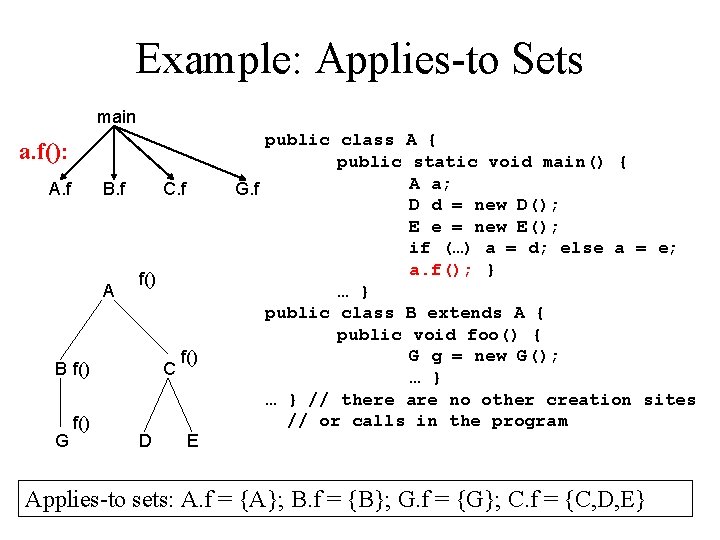
Example: Applies-to Sets main a. f(): A. f B. f A C. f f() B f() G f() C D f() E public class A { public static void main() { A a; G. f D d = new D(); E e = new E(); if (…) a = d; else a = e; a. f(); } … } public class B extends A { public void foo() { G g = new G(); … } // there are no other creation sites // or calls in the program Applies-to sets: A. f = {A}; B. f = {B}; G. f = {G}; C. f = {C, D, E}

Observations on CHA • Do we need to resolve the class of the receiver uniquely in order to devirtualize a call?

Rapid Type Analysis • Improves on Class Hierarchy Analysis • Interleaves construction of the call graph with the analysis (known as on-the-fly call graph construction) • Only expands calls if it has seen an instantiated object of appropriate type • Makes assumption that the whole program is available! David Bacon and Peter Sweeney, “Fast Static Analysis of C++ Virtual Function Calls”, OOPSLA ‘ 96

Example public class A { public static void main() { A a; D d = new D(); E e = new E(); if (…) a = d; else a = e; a. f(); } … } public class B extends A { public void foo() { G g = new G(); … } // there are no other creation // sites or calls in the // program RTA starts in main; Sees D, and E are instantiated; Expands a. f() into C. f() only. Never reaches B. foo() and never sees G instantiated. main A. f B. f C. f G. f

RTA • Keeps two sets, I (the set of instantiated classes), and R (the set of reachable methods) • Starts from main, I = {}, R = {main} • Analyze calls in reachable methods: r. f() – Finds potential targets according to CHA: X. f, Y. f, etc. – If Applies-to(X. f) intersects with I, make X. f a real target, and add X. f to R • Analyze instantiation sites in reachable methods: r = new A() – Add A to I – Find all analyzed calls r. f() with potential targets X. f triggered by A (i. e. , A in Applies-to(X. f) at r. f()). Make X. f a real target, and add X. f to R.

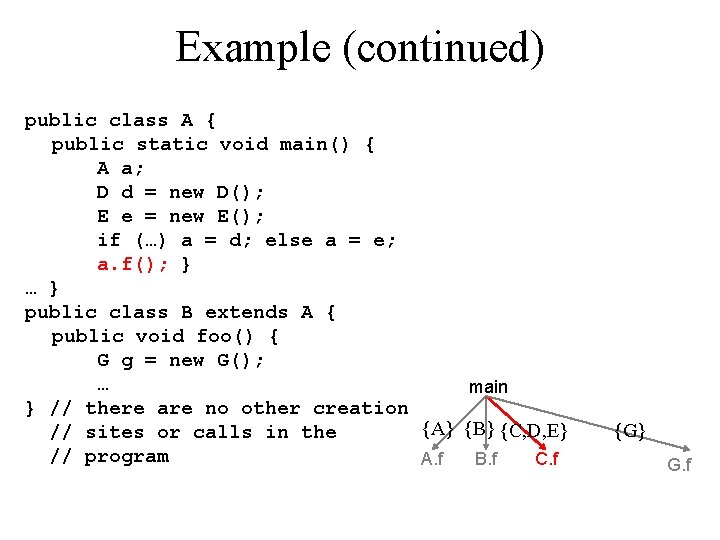
Example (continued) public class A { public static void main() { A a; D d = new D(); E e = new E(); if (…) a = d; else a = e; a. f(); } … } public class B extends A { public void foo() { G g = new G(); … main } // there are no other creation {A} {B} {C, D, E} // sites or calls in the // program A. f B. f C. f {G} G. f

Comparisons Bacon-Sweeny, OOPSLA’ 96 class A { public : virtual int foo() { return 1; }; }; class B: public A { Public : virtual int foo() { return 2; }; virtual int foo(int i) { return i+1; }; }; void main() { CHA resolves result 2 call B* p = new B; uniquely to B. foo(); however, it int result 1 = p->foo(1); does not resolve result 3. int result 2 = p->foo(); A* q = p; RTA resolves result 3 uniquely int result 3 = q->foo(); because only B has been } instantiated.

Type Safety Limitations • CHA and RTA assume type safety of the code they examine! //#1 A foo() void* x = (void *) new B; B* q = (B*) x; //a safe downcast int case 1 = q->foo() B foo() foo(int) //#2 void* x = (void *) new A; B* q = (B*) x; //an unsafe downcast int case 2 = q->foo()// what happens here? //#3 void* x = (void *) new A; B* q = (B *) x; //an unsafe downcast int case 3 = q->foo(66); // what happens here?

Call Graphs • Class analysis: Given a reference variable x, what are the classes of the objects that x refers to at runtime? – We saw CHA and RTA • Deal with polymorphic/virtual calls: x. m() – Compilers: can we devirtualize a virtual call x. m()? – Software engineering • Construct the call graph of the program

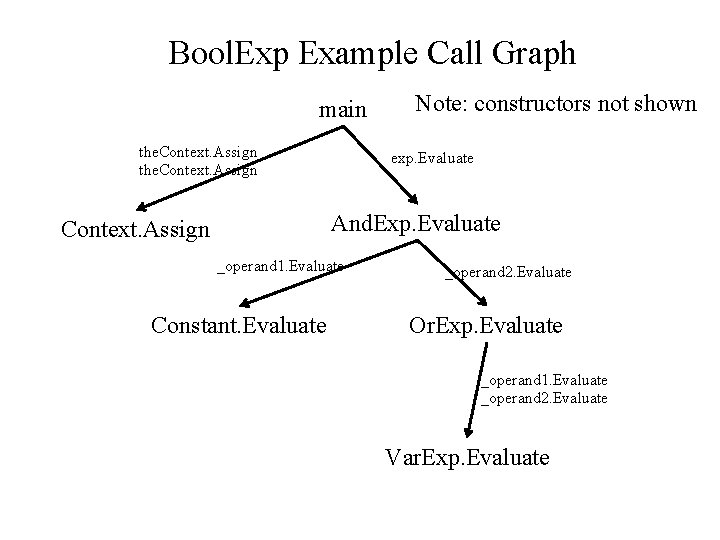
Bool. Exp Example Call Graph main the. Context. Assign Note: constructors not shown exp. Evaluate And. Exp. Evaluate Context. Assign _operand 1. Evaluate Constant. Evaluate _operand 2. Evaluate Or. Exp. Evaluate _operand 1. Evaluate _operand 2. Evaluate Var. Exp. Evaluate

Constructing the call graph: A General Reachability Model • Your project - a series of class analyses for Java – CHA, RTA, etc. • Constructing the call graph using CHA – Function dispatch: the effect of run-time virtual dispatch – As a reachability computation starting from main() • Constructing the call graph using RTA – Minor, but important changes from CHA

dispatch(call_site s, receiver_class rc) sig = signature_of_static_target(s) ret = return_type_of_static_target(s) c = rc; while (c != null) { if class c contains a method m with signature sig and return type return m; c = superclass(c) } print “error: this should be unreachable!!!”

Reachability Computation Queue worklist Call. Graph worklist. add. At. Tail(main()) Graph. add. Node(main()) while (worklist. not. Empty()) { m = worklist. get. From. Head(); process_method_body(m); }

process_method_body(method m) for each call site s inside m if s is a static call, a constructor call or a super call add_edge(s) if s is a virtual call x. n(…) { rcv_class = type_of(x) for each non-abstract class c in cone(rcv_class) { n’ = dispatch(s, c); add_edge(s, n’); } }

add_edge(call_site s, run_time_target n’) // for virtual calls m = encl_method(s); if n’ is not in Graph. add. Node(n’); worklist. add. At. Tail(n’); Graph. add. Edge(m, n’, s); // an edge from m to n labeled with s add_edge(call_site s) // for static calls, constructor calls and super calls // same…

Example class A { class B extends A { void m() {} void m() { void n() {} A x = new A(); static void main(…) { x. n(); // c 3 B b = new B(); } b. m(); // c 1 } A a = b; class C extends B { a. m(); // c 2 void m() {} } void n() {} } }

Bool. Exp Hierarchy Example • Construct the call graph using CHA? • RTA?