COURSE 3 LESSON 8 4 Solve a Simpler

COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern A meeting is attended by 8 people. Each person shakes hands once with every other person at the meeting. How many handshakes will there be? Each person at the meeting shakes hands once with every other person. The goal is to find the total number of handshakes. You can solve a simpler problem by looking for a pattern in meetings with fewer than eight people. 8 -4

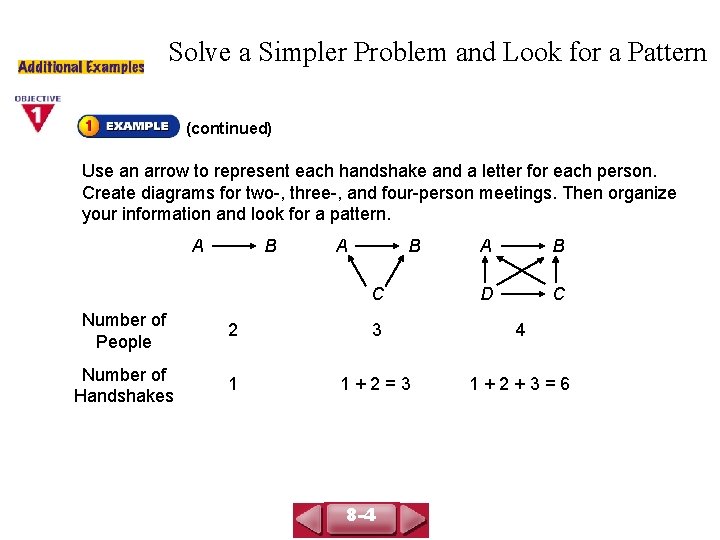
COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern (continued) Use an arrow to represent each handshake and a letter for each person. Create diagrams for two-, three-, and four-person meetings. Then organize your information and look for a pattern. A B C A B D C Number of People 2 3 4 Number of Handshakes 1 1+2=3 1+2+3=6 8 -4

COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern (continued) Make a conjecture about how to find the number of handshakes in a meeting with n people. The total number of handshakes is the sum of positive integers from 1 to n – 1. Eight people: 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 handshakes. To test your conjecture, draw a diagram of a five-person meeting. 8 -4

COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern You place one grain of rice on the first square of a checkerboard, two grains on the next square, four on the next, and eight on the next (doubling each time). After you put 1, 024 grains on a square, how many squares will have rice on them? The goal is to find the number of squares on which you place 1, 024 grains of rice if you place one grain on the first square of a checkerboard, two grains on the second square, four on the third, and eight on the fourth (doubling each time). Solve a simpler problem similar to the given problem. Look for a pattern to help you solve the original problem. 8 -4

COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern (continued) Consider the first four squares. Then organize your data. Square # #1 #2 #3 #4 Number of grains 1 2 4 8 Number of grains 20 = 1 21 = 2 22 = 4 23 = 8 Using inductive reasoning, you can make this conjecture about the number of grains placed on square n: the number of grains placed on square n is 2(n– 1). Since 1, 024 = 210, n – 1 = 10 and n = 11. Thus, 1, 024 grains of rice will be placed on square #11. Eleven squares will have rice on them. To test your conjecture, extend the chart to square #5. 8 -4

COURSE 3 LESSON 8 -4 Solve a Simpler Problem and Look for a Pattern How many diagonals can a 15 -sided polygon have? 90 8 -4