Cours de Traitement Numrique du Signal Chapitre 1

Cours de : « Traitement Numérique du Signal » Chapitre 1: Transformée en Z Formation Master 1: - Systèmes de Télécommunications - Electronique des Systèmes Embarqués - Instrumentation Prè-requis : - Notions de bases de traitement du signal - Mathématiques pour le signal discret - Transformée de Fourier et de Laplace Présenté par : Pr. Amar Mezache 1

Objectifs du cours Numérisation des signaux. Représentations fréquentielles des signaux et analyse des systèmes à temps discret. Maîtriser les technique de synthèse du filtrage numérique. Acquérir les outils nécessaires pour l’étude des Processus stochastiques. Transformée de Fourier discrète (TFD) et algorithmes FFT. 2

Objectifs Contenu du Chapitre 1 Spectre du signal échantillonné. Théorème de Shannon. Transformation en Z (TZ) à partir de la transformée de Laplace Propriétés de la TZ. Transformée en Z inverse. Illustrations par des fonctions Matlab. 3

Pourquoi la transformée en Z ? Etude de la stabilité des systèmes discrets. Synthèse des filtres numériques. Design des correcteurs numériques. Communications digitales. 4

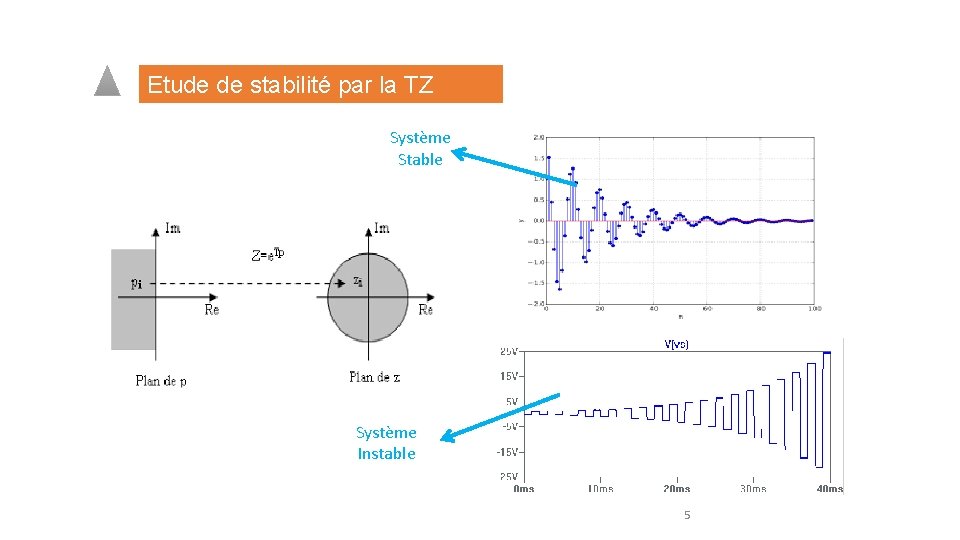
Etude de stabilité par la TZ Système Stable Système Instable 5

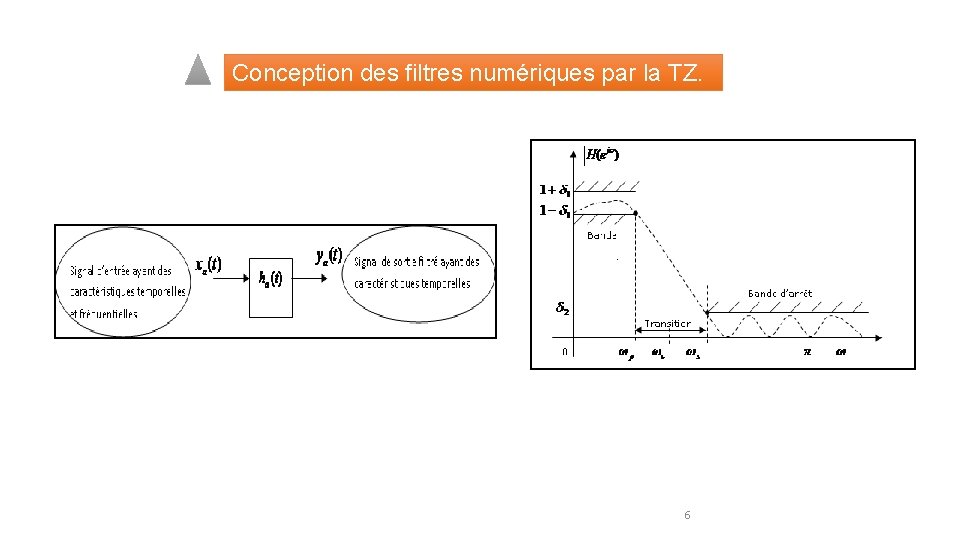
Conception des filtres numériques par la TZ. Changement de caractéristiques temporelles et fréquentielles Gabarit du filtre passe-bas 6

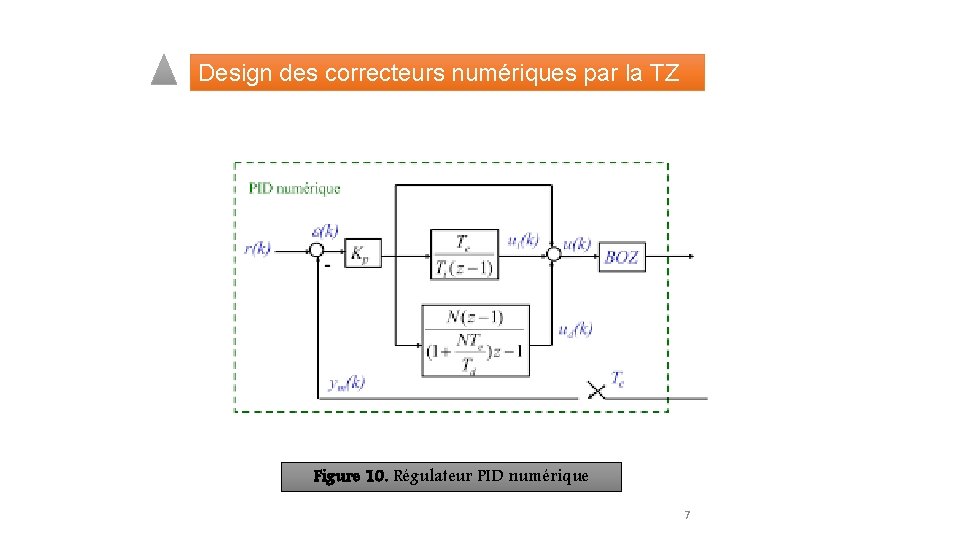
Design des correcteurs numériques par la TZ Figure 10. Régulateur PID numérique 7

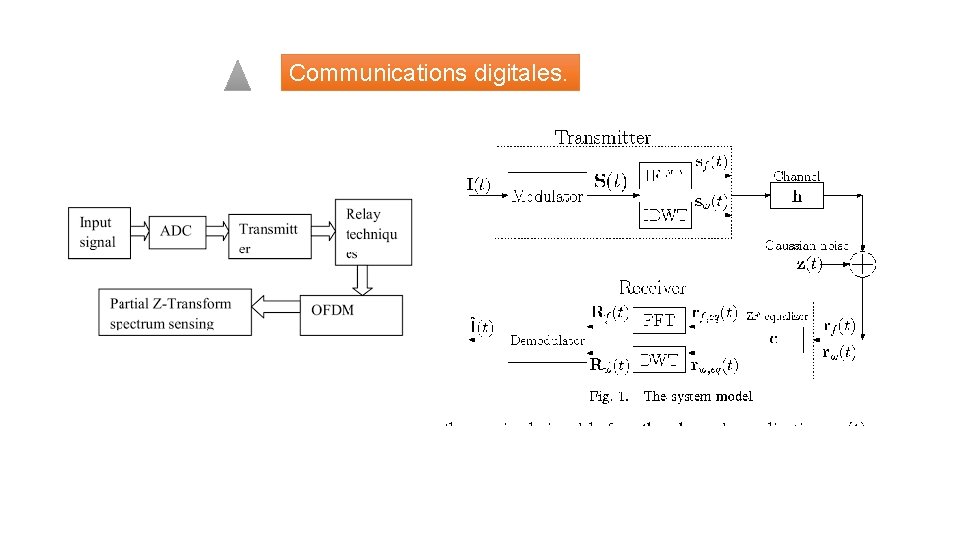
Communications digitales.

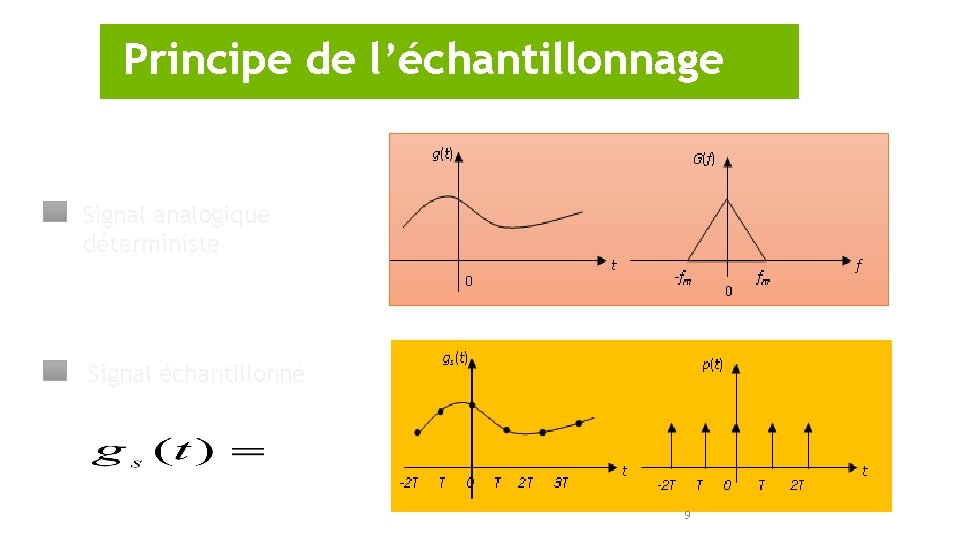
Principe de l’échantillonnage Signal analogique déterministe Signal échantillonné 9

Spectre du signal échantillonné

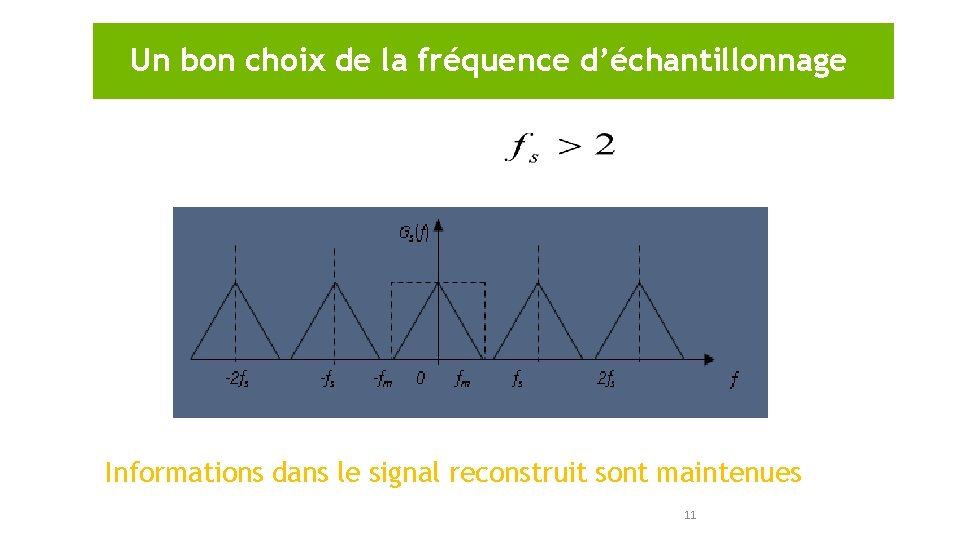
Un bon choix de la fréquence d’échantillonnage Spectre non-chevauché: Informations dans le signal reconstruit sont maintenues 11

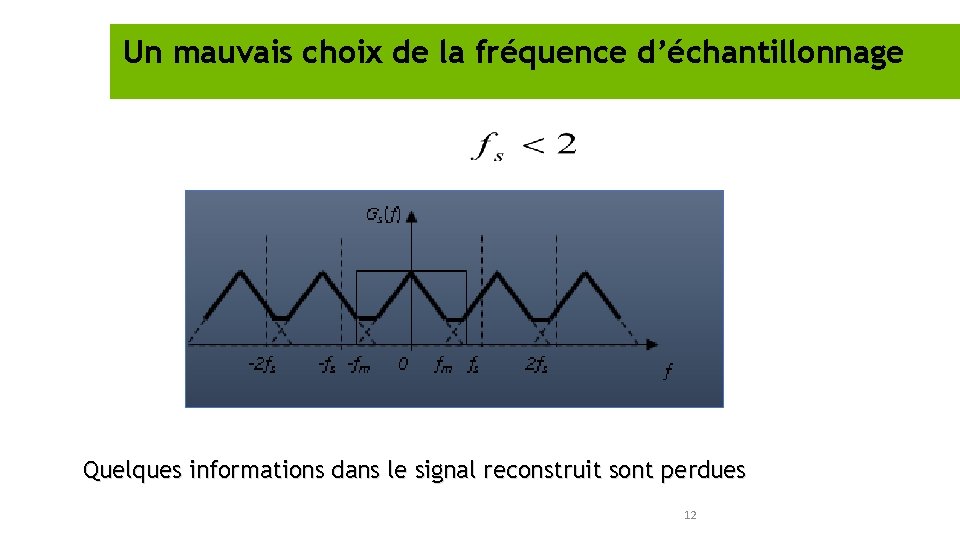
Un mauvais choix de la fréquence d’échantillonnage Spectre chevauché : Quelques informations dans le signal reconstruit sont perdues 12

Théorème de Shannon Claude Elwood Shannon (30 avril 1916 - 24 février 2001) 13

Transformée en Z On pose Un système causal 14

Relation avec la transformée de Fourier X(z) possède un domaine de convergence qui est en général un anneau centré sur l’origine de rayons R 1 et R 2. 15

Propriétés de la TZ Linéarité : Décalage temporel : Avance : Convolution : Multiplication par une exponentielle : 16

Propriétés de la TZ Théorème de la valeur initiale : Théorème de la valeur finale : Multiplication par la variable d’évolution : 17

Transformée en Z inverse. Méthode de la Table de transformations en Z usuelles. Méthode de fractions rationnelles. Méthode en série de puissances Méthode de l’inversion de la formule (Résidus) 18

Transformée en Z inverse Le théorème des résidus est souvent utilisé pour déterminer x(n) Le résidu à un pôle z=a d’ordre q de la fonction Série géométrique : avec est donné par : et 19

Transformées en Z usuelles 20

Commandes Matlab correspondantes Calcul de la transformée en Z : >> syms z n >> ztrans(1/4^n) ans =z/(z - 1/4) Calcul de la transformée en Z inverse : >> syms z n >>iztrans((6 -9*z^-1)/(1 -2. 5*z^-1+z^-2)) ans =2*2^n + 4*(1/2)^n 21

Commandes Matlab Calcul de la série en puissance : >> [q, r]=deconv(b, a) Exemple : >> b=[1 2 1]; >> a=[1 -1 0. 356]; >> n=5 n = 5; >> b=[b zeros(1, n-1)]; >> [x, r]=deconv(b, a); >> disp(x) 1. 0000 3. 6440 2. 5760 1. 2787

Commandes Matlab Calcul des Fractions rationnelles: Exemple : >> [r, p, k]=residuez(b, a); >> [r, p, k]=residuez([1, 2, 1], [1, -1, 0. 3561]) r= -0. 9041 - 5. 9928 i -0. 9041 + 5. 9928 i p= 0. 5000 + 0. 3257 i 0. 5000 - 0. 3257 i k= 2. 8082 23

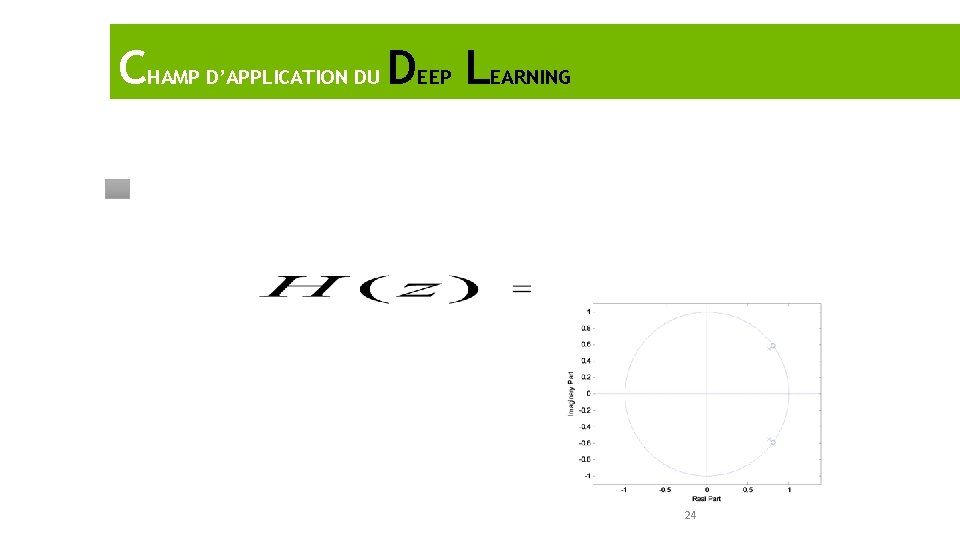
CHAMP D’APPLICATION DU DEEP LEARNING Calcul du diagramme pôles/zéros: >> zplane(b, a) Exemple : >> b=[1 -1. 618 1]; >> a=[1 -1. 5161 0. 878]; >> roots(a) ans = 0. 7581 + 0. 5508 i 0. 7581 - 0. 5508 i >> roots(b) ans = 0. 8090 + 0. 5878 i 0. 8090 - 0. 5878 i >> zplane(b, a) 24

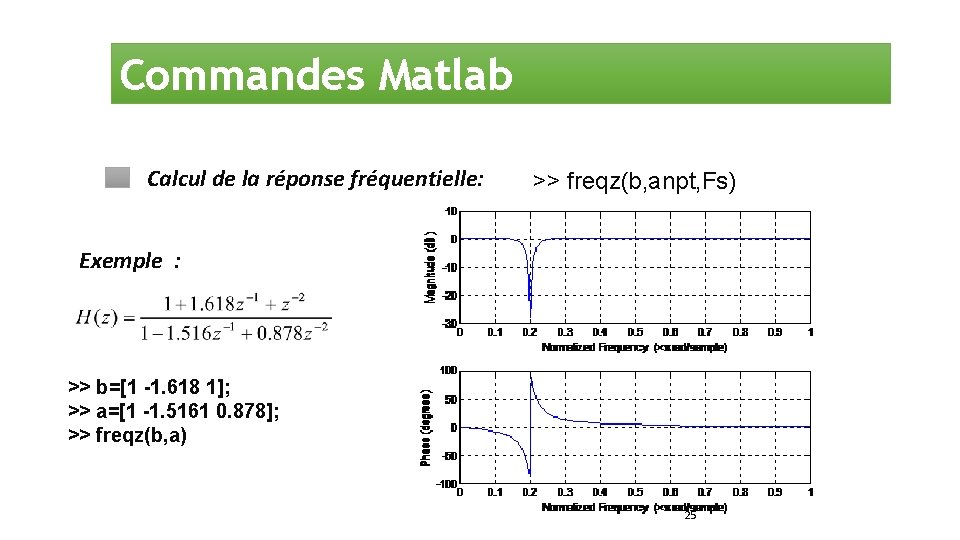
Commandes Matlab Calcul de la réponse fréquentielle: >> freqz(b, anpt, Fs) Exemple : >> b=[1 -1. 618 1]; >> a=[1 -1. 5161 0. 878]; >> freqz(b, a) 25

Série d’exercices de TD Ex #1 : a- Calculer la transformée en Z (T. Z) de chaque signal analogique xa(t) suivant : - xa(t)=u(t) avec u(t)=1 pour t>0 et 0 ailleurs - xa(t)= e-at u(t) - xa(t)=tu(t) b- Déterminer la TZ des séquences suivantes : - x(n)= an - x(n)=n-5 - x(n) = n+1 - x(n) = (n + 2)² - x(n) = 2 nn 2 c- Soit un système linéaire invariant dans le temps avec la réponse impulsionnelle : - Déterminer la TZ de la séquence de sortie y(n). 26

Série d’exercices de TD Ex #2 : a- Calculer la T. Z inverse (TZI) de la fonction ci-dessous : b- Déterminer la TZI de X(z) par la méthode de fraction rationnelle c- Calculer la TZI de la fonction X(z) par la méthode en série de puissance d- Calculer la TZI de la fonction suivante utilisant la méthode des résidus 27

Références [1] M. Barkat, “Signal Detection and Estimation“, Second Edition, Artech House, Boston, MA, SA, 2005 [2] A. V. Oppenheim and R. W. Schafer, ‘Digital Signal Processing’, Prentice-Hall International Editions, 1975. [3] M. Kunt, ‘Traitement numérique des signaux’, Deuxième édition Presses polytechniques Romandes, CH-1015, Lausanne, Suisse, 1989. [4] B. C. Kuo, ‘Digital Control Systems‘, Second Edition, Saundders College Publishing, Harcourt Brace Jovanovich College Publisher, 1992 [5] B. Porat, ‘A course in Digital signal Processing’, John Wiley & Sons, INC, 1997. [6] Z transform: https: //en. wikipedia. org/wiki/Z-transform [7] Matlab command: https: //www. mathworks. com/products/matlab. html. [8] Frédéric De coulon, ‘Théorie et traitement des signaux’, Dunod 1985, Paris, France. 28

MERCI POUR VOTRE ATTENTION